一種混合結構柔性臂的軌跡跟蹤控制器設計

宋艷東 胡海東 秦 嶺 范 普

(內蒙古科技大學 信息工程學院，內蒙古 包頭 014010)

1 混合結構柔性臂建模

1.1 假設模態法描述柔性形變

本文中，將所有連桿均視為Euler-Bernoulli 梁。根據假設模態法[1]，柔性偏差可表示為：

其中，φ (x)為模態函數，q(t)為模態坐標。

由于混合結構柔性臂由兩節連桿嵌套組成，因此將連桿分為固定段、重疊段和延伸段建立坐標系，如圖1所示。

圖1 混合結構柔性臂坐標系模型

由于混合結構柔性機械臂系統模型比較復雜且耦合程度高，因此本文將系統狀態變量分為剛性結構變量u0和柔性結構變量u2[2]。其表達式分別為：

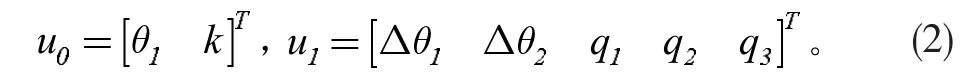
1.2 剛性結構部分建模

由剛體拉格朗日平衡方程[3]，可推導混合結構柔性機械臂剛性結構部分動力學方程為：

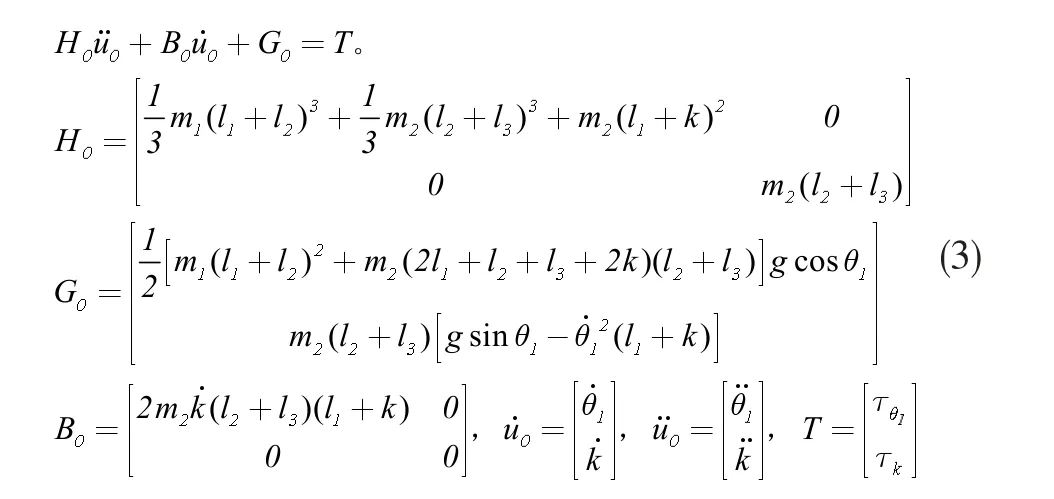
1.3 柔性結構部分建模

當考慮混合結構柔性機械臂的撓曲變形時，連桿上任意一點p 的位置矢量表示為：

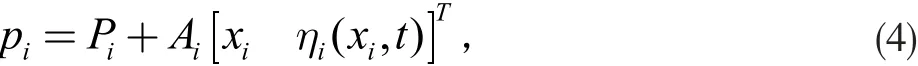
其中，Pi為該點所在參考坐標系原點在基坐標系中的位置向量；Ai為該點所在參考系坐標系到基坐標系的轉換矩陣；ηi表示該點的柔性偏差。

由于 Δθ1, Δθ2為微小的柔性偏差角度，所以忽略二階及以上的項，則p 點速度表達式為：

則系統動能表示為：

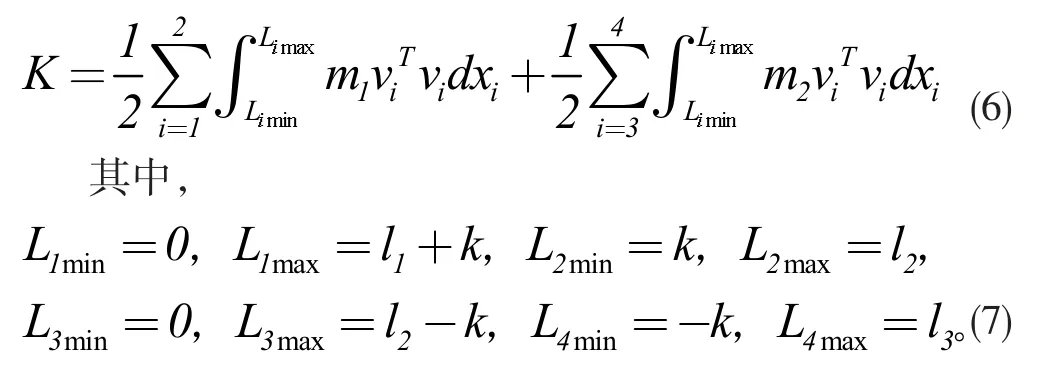
對于p 點的勢能，依據動能計算方法，可表示為：

采用拉格朗日方程[4]，

將式(6)和(8)代入式(9)，即可得柔性偏差部分動力學方程為：

其中，F=［f1f 200 0］T?對于上式，參數H,B,G,K都是關于剛性關節變量 θ1和k的函數，則方程(10)可視為一個線性時變系統。

2 軌跡跟蹤控制器設計

混合結構柔性臂軌跡跟蹤控制器的總體設計思路為給定參考軌跡，將滑模控制器控制力矩，輸入到剛性結構部分動力學模型中得到剛性關節變量的運動軌跡，然后將實際運動軌跡與參考軌跡的偏差反饋至滑模控制器中形成閉環控制鏈。將剛性關節變量輸入到柔性結構部分線性動力學方程中進行求解，即可得到柔性結構狀態變量的變化情況。

2.1 滑模控制器的設計

定義Lyapunov 函數

則

設計控制律為

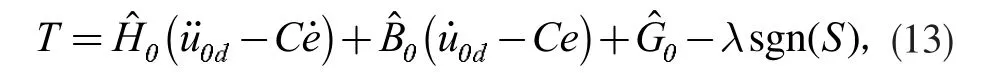
于是

令

2.2 通過BLF 方法對部分輸出變量施加約束

定義輸出偏差為

定義Barrier Lyapunov 函數

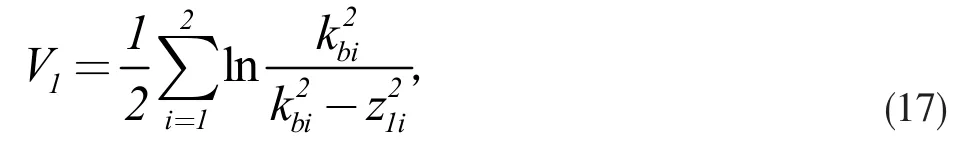
則

設計穩定函數

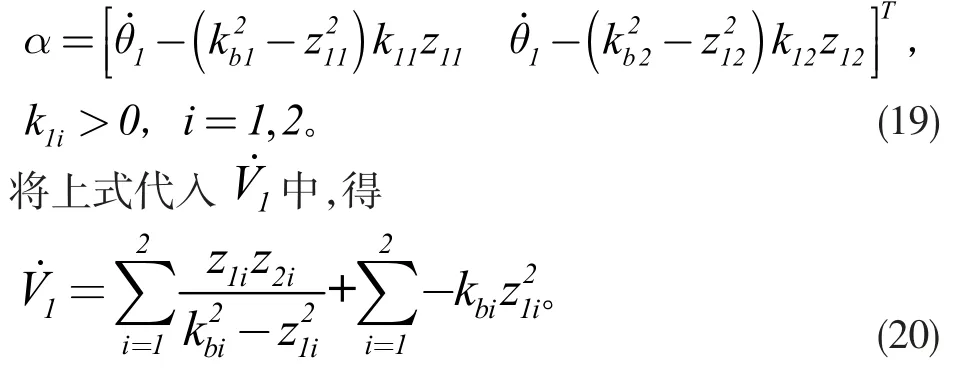
(2)定義Lyapunov 函數

對時間T 求導并結合式(10)、(20)，有：

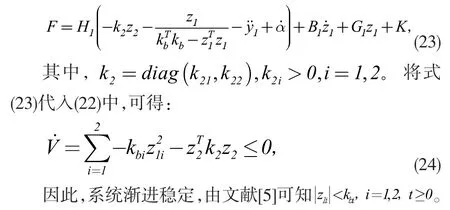
3 仿真結果

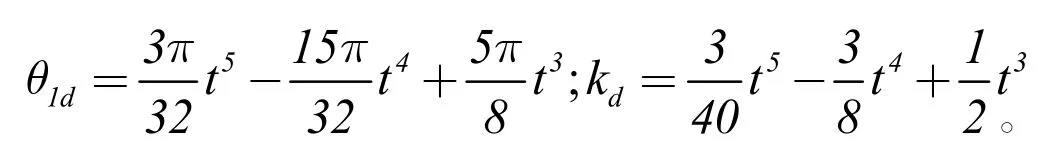
兩關節變量初始狀態為：θ1=0.06rad,k=0.02m，仿真時長為6s。仿真結果如圖2 所示。

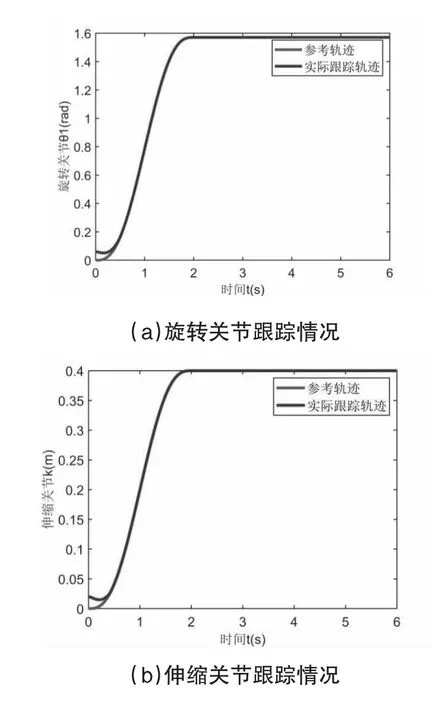
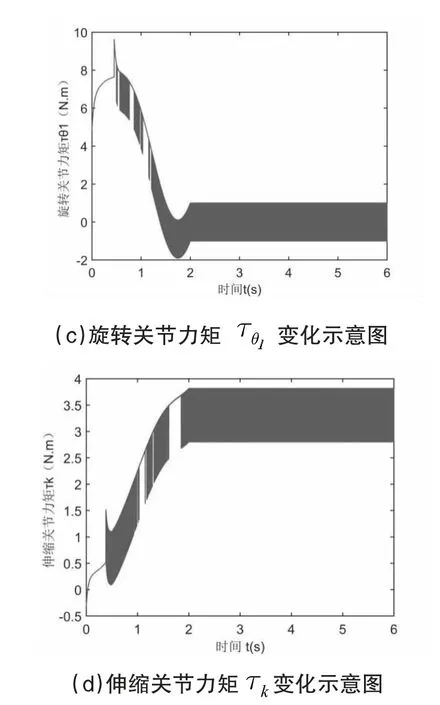
圖2 旋轉關節與伸縮關節軌跡跟蹤與力矩變化示意圖

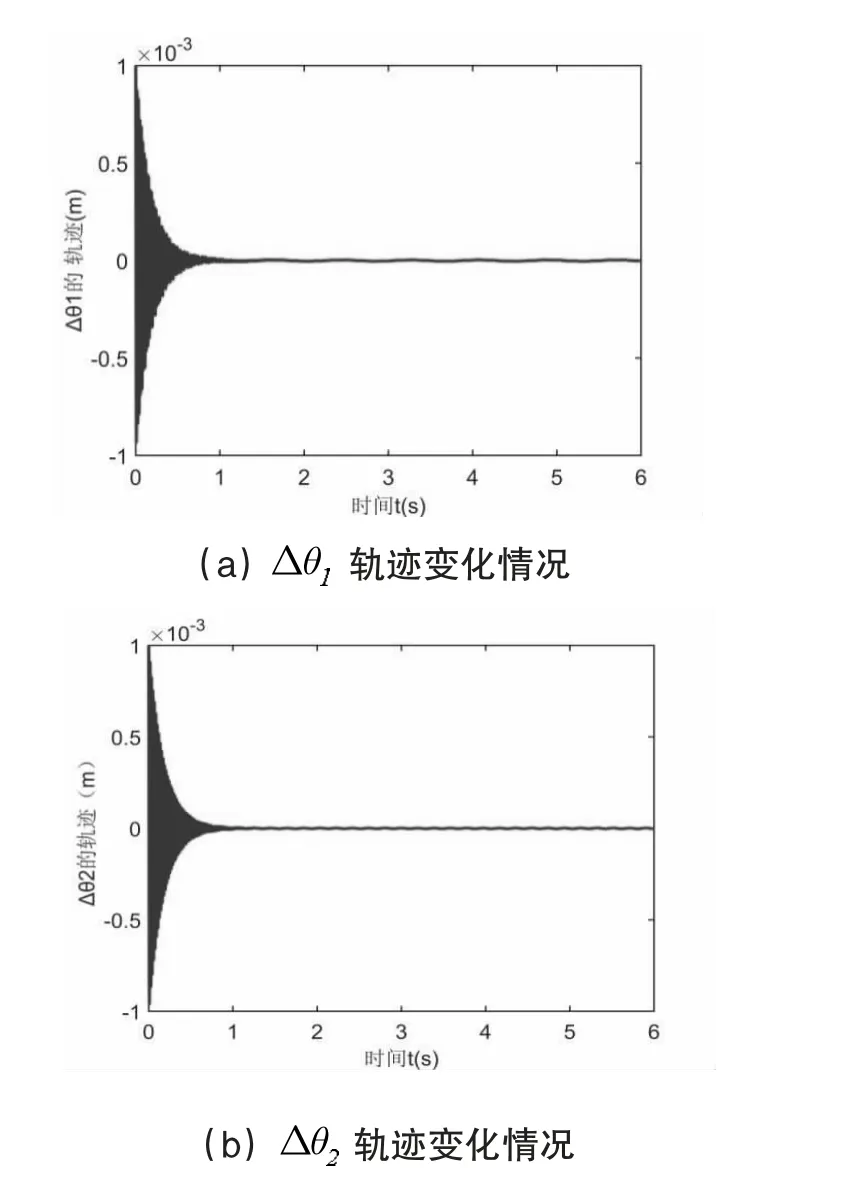
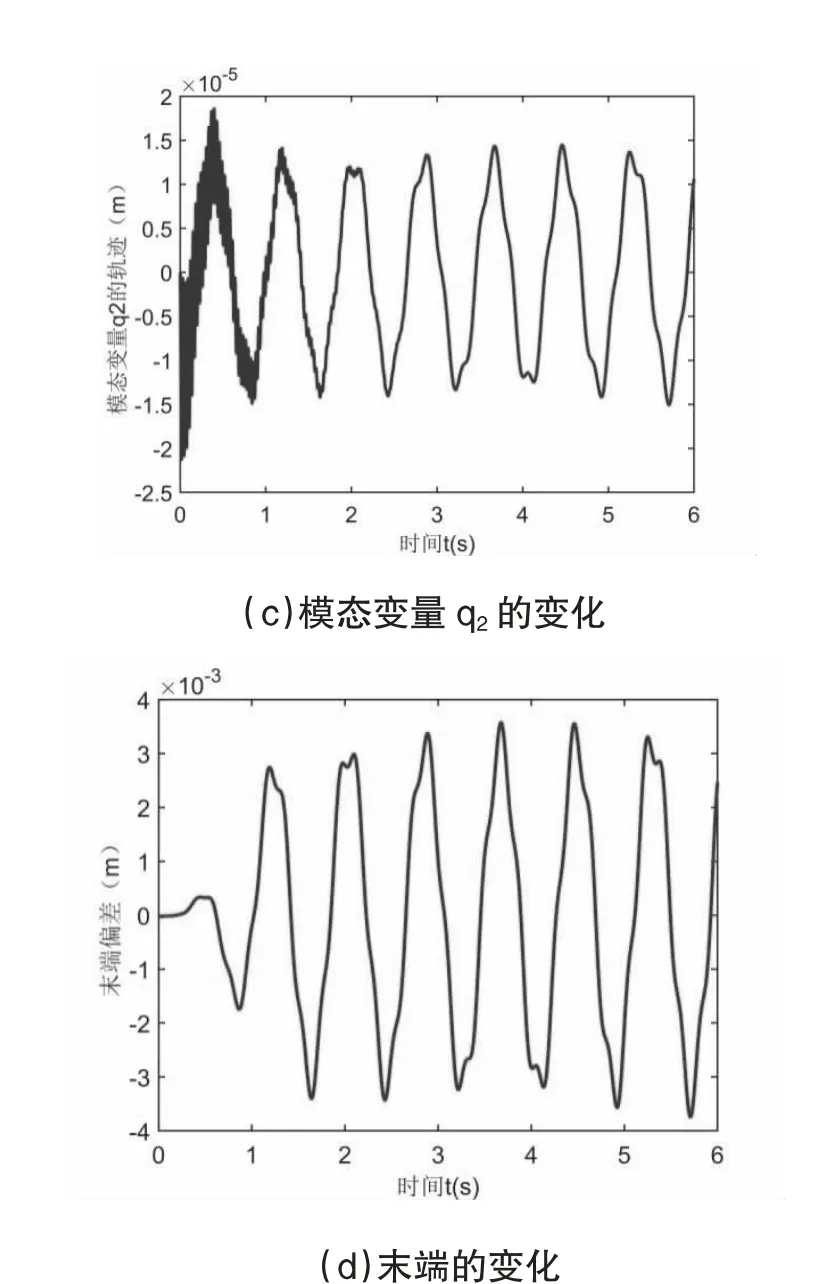
圖3 柔性角度偏差 Δ Δ、模態變量q2 及末端隨時間的變化

4 結論

本文針對混合結構柔性臂的結構特點，將系統分為固定段、重疊段、延伸段，并將系統分解為剛性部分和柔性部分分別進行建模。設計滑模控制器對剛性關節軌跡進行跟蹤，并針對控制過程中出現柔性偏差角度變大的問題，采用Barrier Lyapunov 函數結合反演的方法，實現對柔性偏差角度的輸出約束。