復式斷面明渠湍流的統計特征和擬序結構
胡德芳,俞華鋒,陳 勇,劉 宇,及春寧*
(1.中國三峽新能源(集團)股份有限公司江蘇分公司,南京 210000; 2.中國電建集團華東勘測設計研究院有限公司,杭州 311122; 3.天津大學 水利工程仿真與安全國家重點實驗室,天津 300072)
具有深槽和淺灘特征的復式斷面河道在坡度較緩的平原地區常見,受季節影響,其徑流量及水深變化很大。研究表明,復式斷面河道在深槽和淺灘的邊角處出現邊角渦,形成二次環流[1]。盡管復式斷面河道的二次環流強度較主流小一個量級,但其對污染物擴散、河床沖蝕、河形塑造等有明顯影響。
復式斷面明渠(河道)在斷面內二次環流與各向異性的湍流雷諾應力有關,被稱為第二類普朗特二次流。Demuren和Rodi[2]認為淺灘和深槽交界邊角處的湍流雷諾應力梯度是產生復式斷面明渠二次環流的原因。馬良棟等[3]進一步指出,二次環流是雷諾應力梯度和壓力梯度相平衡的結果。
在實驗研究方面,研究者對復式明渠二次流流速和雷諾應力、最大二次流流速位置[1]、污染物濃度分布[4]等進行了研究,發現二次流流速約為主流最大流速的4%,出現在淺灘和深槽的連接處。Sanjou和Nezu[5]采用多層掃描粒子圖像測速(PIV)技術測量了復式明渠二次環流,并分析了流向渦三維結構。Watanabe等[6]采用粒子示蹤(PTV)技術測量了非對稱復式斷面明渠二次環流,同時利用流動顯示技術分析了淺灘和深槽的湍流擬序結構。
在數模研究方面,Keller和Rodi[7]求解水深平均平面二維雷諾時均N-S方程,模擬了復式明渠流動。但當斷面寬深比B/H較大時,平均流速U和壁面應力τw在深槽和淺灘結合處與實驗結果相差較大。Krishnappan和Lau[8]開展了復式明渠湍流的三維數值模擬,得到了壁面應力τw與順流向流速U分布,在深槽和淺灘結合處模擬結果與實驗結果吻合較好。梁愛國和槐文信[9]開展了三維數值模擬,研究了復式明渠流動中污染物輸運,探討了自由表面方法對模擬結果的影響。隨著計算能力的提高,湍流大渦模擬在復式斷面明渠二次環流的研究中得到了應用,其模擬結果更加準確。Thomas和Williams[10]對復式明渠二次環流開展了大渦模擬,比較分析了亞網格尺度模型對結果的影響。許棟等[11]利用大渦模擬研究了復式斷面明渠淺灘深度和雷諾數對湍流結構的影響。曾誠等[12]提出了一種壁面建模的大渦模擬方法,研究了復式斷面明渠湍流的流場特征。陳勇等[13]對復式斷面明渠湍流開展了直接數值模擬,討論了二次流流速和雷諾應力等的分布特征。此外,許棟等[14]采用小參數攝動理論推導了小角度斜向入流條件下復式斷面明渠流速重分布線性理論。吉祖穩等[15]采用實體模型概化水槽研究了復式河道灘槽泥沙粒徑的分布特征。方崇和郝嘉凌[16]采用粒子圖像測速儀(PIV)實驗方法,探究了不同工況下恒定流流速剖面、紊流度和底邊界層厚度等參數的變化規律。夏鵬飛等[17]針對 90°豎直彎管內的流動特征進行了三維數值模擬,分析了不同水頭條件下,彎管內的二次流動的特征。
可見,已經開展的復式斷面明渠二次環流研究多采用雷諾時均N-S方程或者大渦模擬開展,但由于兩種模擬方法均采用經驗性的湍流模型對控制方程進行封閉,難以對于湍流擬序結構進行精確模擬,因此也難以深入揭示二次環流產生的機制。湍流直接數值模擬不采用任何湍流模型,有助于從機理上分析二次環流產生的原因。本文采用直接數值模擬,研究復式斷面明渠湍流的統計特征和二次環流產生機制。
1 控制方程和邊界條件
粘性不可壓縮流動的控制方程如下
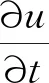
(1)
▽·u=0
(2)
式中:u為速度矢量;t為時間;p為壓強;v為運動粘滯系數;▽為梯度算子;g為重力加速度矢量。
對控制方程采用具有二階時間精度的Adams-Bashforth格式進行時間離散,時間離散后的控制方程守恒形式如下
(3)
▽·un+1=0
(4)
式中:h=▽·(-uu+v(▽u+▽uT))由對流項與擴散項組成,上標T為矩陣轉置,上標n+1、n和n-1為時間步。對控制方程(式3~4)采用具有二階空間精度的中心差分格式進行空間離散。
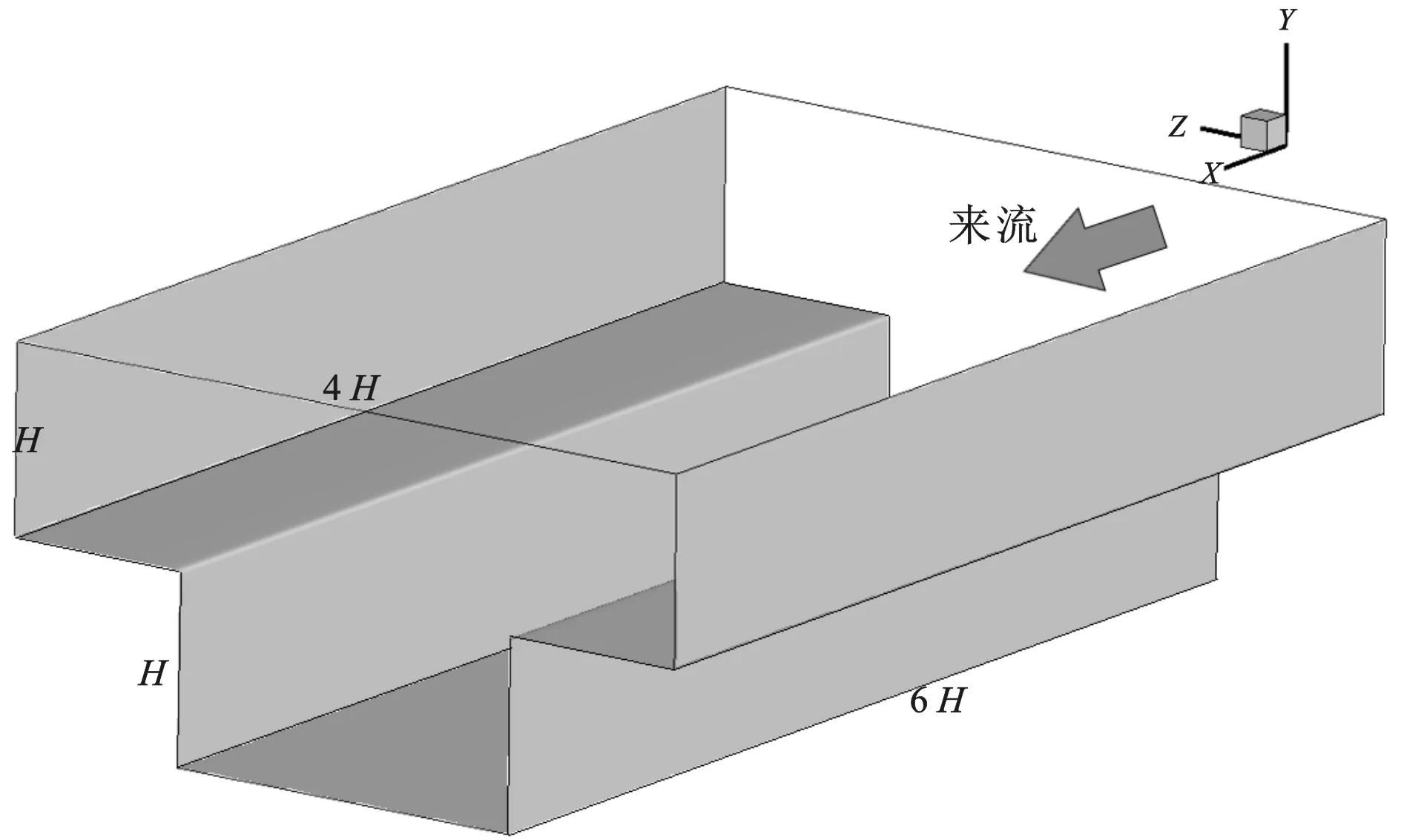
圖1 復式斷面明渠湍流計算域示意圖Fig.1 The computational domain of compound open channel flows
如圖1所示,復式斷面明渠的流向(X)和展向(Z)長度分別為6H和4H,其中,H為淺灘處水深。左右各有一個淺灘,寬度為H。中間深槽的水深為2H,寬度為2H。明渠頂面采用自由滑移(free-slip)邊界條件,底面和邊壁采用不可滑移(no-slip)邊界條件,X方向的端面采用周期(periodicity)邊界條件,即兩個端面上的所有物理量相等,以模擬無限長的計算域。上部區域和下部深槽分別采用均勻網格進行空間離散。上部區域網格沿流向、豎向和展向的網格點數分別為192、64和256。下部深槽網格沿流向、豎向和展向的網格點數分別為192、64和128。在流向上施加體積力驅動,基于摩阻流速uτ和淺灘水深H的雷諾數為Reτ=uτH/v=180。由此可以計算得到無量綱的網格大小分別為△x+=5.62,△y+=△z+= 2.81,滿足明渠湍流直接數值模擬的要求[18],即第一層速度網格點的無量綱壁面距離在1.0附近(本文中速度定義在網格中心,第一層速度網格點的無量綱壁面距離約為1.4)。
2 驗證算例
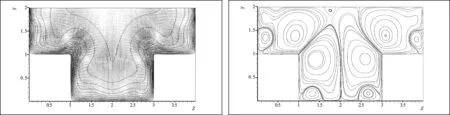
本文選取平板邊界層湍流對數值模擬的精度進行驗證,計算域尺寸為6H×H×4H,采用均勻網格,沿流向、豎向和展向的網格點數分別為128、96和128。雷諾數為Reτ=180。計算域的流向和展向為周期邊界,底部為不可滑移邊界,頂部為自由滑移邊界。圖2給出了無量綱順流向時均流速和無量綱紊動強度與Moser等[19]結果的對比,兩者吻合良好,證明了本文所采用數值方法具有較高的精度和可靠性。從圖中可以看出,流向時均流速剖面在近壁處(y+<5)呈線性分布,這符合粘性底層的速度分布特征。在對數率區(y+>30),流向時均流速符合對數分布。而在過渡區(5 圖2 平板邊界層湍流的時均流速和紊動強度Fig.2 Time averaged velocity and turbulence intensities of turbulent boundary layer flow over a flat plate 圖3給出了復式斷面明渠平均流速的等值線云圖。如圖3-a所示,流向平均流速U在截面中央自由表面處(Z=2H,Y=2H)取最大值,為Umax=16.912ut。據此,可計算出基于最大流速的雷諾數為Remax=UmaxH/v=3 044,屬充分發展湍流。豎向平均流速V在(Z=1.1H,Y=0.9H)處取最大值,為0.742uτ,約為U最大值的4.4%。此處,深槽底部的流體被帶到了復式斷面的上部。在深槽的中央,豎向平均流速方向向下,上部流體又被帶到了深槽底部。兩個過程形成一個閉合的環路,構成了深槽和斷面上部流體交換的通道。橫向平均流速W最大值在(Z=0.9H,Y=1.1H)和(Z=3.1H,Y=1.1H)處取得最大絕對值,為0.797ut,約為U最大值的4.7%。流體在此處集中由淺灘流向深槽。與之相反,在(Z=0.9H,Y=1.8H)和(Z=3.1H,Y=1.8H)鄰近自由表面附近,流體由深槽流向淺灘,與表面和深槽中的反向流動構成閉合環路。 3-a 流向速度U 3-b 豎向速度V 3-c 展向速度W圖3 復式斷面明渠平均流速云圖 圖4給出了時間平均后的復式斷面明渠二次環流速度矢量和流線圖。可以看出,在復式斷面上存在4對左右對稱的漩渦結構,深槽和淺灘中各2對。其中,在深槽與淺灘結合處的漩渦尺度最大,幾乎占據了整個斷面,在深槽內的部分叫做“深槽渦”,在淺灘內的部分叫做“淺灘渦”。在淺灘邊璧和深槽底部靠近邊角處也存在漩渦,但尺度較小。此外,在自由表面的中心處也可觀察到小尺度且不穩定的漩渦結構,這與平均時間較短有關。以上結果與Thomas、Williams[10]大渦模擬結果和Tominaga、Nezu[1]的實驗結果一致。深槽與淺灘結合處存在二次流動,方向斜向向上,指向自由表面中部,最大流速約為順流向主流流速的4.5%,如圖4-a所示。另外一方面,此傾斜向上的二次流也對主流流速分布產生影響,深槽與淺灘結合處的主流流速U較周圍主流流速低,如圖3-a所示。這與二次流將靠近壁面的低速流體帶到了流動核心區有關。由于深槽與淺灘結合處存在較強的流動剪切率,可以判斷此處存在復雜的湍流擬序結構。 4-a 速度矢量圖 4-b 環流流線圖圖4 復式斷面明渠時均二次環流 圖5給出了明渠斷面三個方向上紊動強度(Urms、Vrms、Wrms)的云圖。如圖5所示,流向紊動強度Urms主要分布在邊璧和底面附近,最大值約為2.60uτ,在(Z/H=0.15,Y/H=1.6)處取得,其中uτ為壁面摩阻流速。對比可以發現,復式斷面的凸角和凹角處的流向紊動強度差異較大,凸角處的Urms較高,而凹角處較低。此外,邊灘底面處的Urms較小,明顯低于深槽底面的Urms。豎向紊動強度Vrms主要分布在深槽的上部和淺灘的中部,最大值約為1.0uτ,在(Z/H=0.3,Y/H=1.7)處取得。需要說明的是,在自由表面處Vrms為零,這與本文采用自由滑移的邊界條件有關,邊界處豎向速度為零。橫向紊動強度Wrms主要分布在深槽的底部和斷面的中部,其最大值與Vrms的相同,約為1.0uτ,在(Z/H=1.3,Y/H=1.3)處取得。綜合三個方向的紊動強度分布可知,在淺灘和深槽的交接處,Urms、Vrms和Wrms均較高,這與此處大量分布的“發卡”渦有關(見后文分析),導致了深槽和淺灘之間存在強烈的水體交換。 5-a 流向紊動強度Urms 5-b 豎向紊動強度Vrms 5-c 橫向紊動強度Wrms圖5 復式斷面明渠紊動強度云圖 6-a 雷諾應力Tuv 6-b 雷諾應力Tvw 6-c 雷諾應力Twu圖6 復式斷面明渠雷諾應力分布云圖 前述結果分析均表明灘槽結合處存在復雜的漩渦結構,為進一步分析二次環流、湍流強度和雷諾剪切應力在此處較大的原因,本文進一步給出了張量ψ2+Ω2的第二特征值λ2=-1.0的等值面分布,以表示漩渦結構的渦核,其中ψ和Ω分別表示速度梯度張量u的對稱部分和反對稱部分,如圖7所示。此外,圖7中還給出了流向紊動流速u′在壁面附近的分布,深色表示較低的u′(負值)分布,而淺色表示較高的u′(正值)分布。 如圖7-a所示,復式斷面明渠的壁面附近均存在深淺相間的條帶分布,這些條帶的產生與湍流的擬序結構有關,即湍流的“噴發”(ejection)過程將靠近壁面的低速流體提離壁面,形成低速條帶(深色),而湍流的“掃掠”(sweep)過程將遠離壁面的高速流體帶到壁面附近,形成高速條帶(淺色)。湍流的擬序結構是壁面和流動核心區流體交換的機制。此外,圖7還給出了復式斷面明渠湍流三維漩渦結構的軸測圖和俯視圖。可以看出,灘槽結合處漩渦結構尺度較大,且數量較多,這造成了該處二次環流強度、紊動強度和雷諾剪切應力較強。另外,可以觀察到每個流向渦結構下邊均存在一個與之對應的低速條帶。 圖7-b給出了灘槽結合處典型的“發卡”渦結構,等值面上的顏色表示到壁面的距離,深色表示距離壁面較遠,而淺色表示距離壁面較近。可以看出,該“發卡”渦橫跨深槽和淺灘,左側的渦腿位于淺灘上,右側的渦腿位于深槽中,渦頭則位于淺灘和深槽結合處上方。然而,由于灘槽結合處復雜的流動,淺灘上渦腿相對完整,但深槽中的渦腿斷裂。圖7-b同時給出“發卡”渦附近的速度矢量。可以看出,位于深槽中右側渦腿導致周圍的流體發生順時針旋轉,造成了渦腿內側(靠近凸角)流體上升,渦腿外側(遠離凸角)流體下掃。同樣,位于淺灘上的渦腿也導致周圍流體發生了類似的旋轉,但旋轉的方向相反。以上過程誘發了灘槽交界處指向斷面中心的二次流(見圖4-b),即為復式斷面明渠二次環流的形成機制。 7-a 軸測圖 7-b 局部放大圖 7-c 俯視圖圖7 復式斷面明渠湍流漩渦結構與低速條帶 本文應用直接數值模擬方法,對復式斷面明渠湍流的一、二階統計特征和湍流擬序結構進行了研究。首先針對平板邊界層湍流問題對數值方法進行了精度驗證,隨后分析了二次環流強度、紊動強度、雷諾剪切應力的分布特征,最后討論了湍流擬序結構及其誘發二次環流的機制,主要結論如下。 (1)二次環流在深槽與淺灘結合處形成一對主渦,可造成淺灘和深槽強烈的水體交換。灘槽結合處流向平均流速U的等值線受二次環流影響向斷面中心彎曲。豎向平均流速V和橫向平均流速W的最大值分別約為流向主流流速U最大值的4.4%和 4.7%。 (2)在淺灘與深槽結合處,湍流紊動強度(Urms、Vrms、Wrms)和雷諾剪切應力(Tuv、Tvw、Twu)均較大,這與該區域附近存在大量的湍流擬序結構有關。 (3)復式斷面明渠底邊壁和側邊壁均存在隨流擺動的條帶結構,橫跨灘槽結合處的“發卡”渦結構,造成渦腿內側流體上升、外側下掃,誘發了灘槽結合處指向斷面中心的二次環流。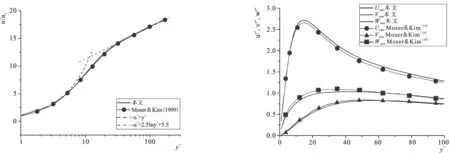
3 結果與討論
3.1 復式斷面明渠湍流一階統計量

3.2 復式斷面明渠湍流二階統計量


3.3 復式斷面明渠湍流三維擬序結構

4 結論

