編程與數學深度融合,助力培養小學生計算思維
何廣林 周明鳳
編程思維是計算機科學中解決問題的思維方式,并不是編寫程序的技巧。具有編程思維的人可以清楚且具體地描述問題并將問題的解決方案表達為信息處理的過程,這個理解問題、尋找路徑的思維過程,可以將復雜的大問題分解為更易于執行和更好理解的小問題。
我國數學教學課程標準中提出的數學思維能力主要是指:會觀察、實驗、比較、猜想、分析、綜合、抽象和概括;會用歸納、演繹和類比進行推理;會合乎邏輯地、準確地闡述自己的思想和觀點;能運用數學概念、思想和方法,辨明數學關系,形成良好的思維品質。
國家將編程教學納入小學課堂,不僅僅是在三維設計、人工智能等信息學科紛紛走進孩子課堂后的必然,也是要將編程的計算思維與學生的學習和生活進行深度融合,讓學生更好地成長。尤其是積極尋求編程與數學知識的結合點,開展有效的小學編程課堂教學。
現以“已知連續幾個奇數的和,求出這幾個數”問題為例,探討如何在編程課堂教學中有效地培養學生的計算思維。
例:已知三個連續奇數的和是99,這三個奇數分別是多少?(《思維訓練》五年級下冊,西師版)
1.觀察分析法:從問題中可以直接看出每個數大概是三十幾,把31加上33,再加上35,剛好就是99。
2. 求平均數法:三個數的和是99,除以3得到它們的平均數,也就是中間那個數,然后減2、加2分別得到其余兩個數。
99÷3=33? ? 33+2=35? ? 33-2=31
3.設未知數法:? a,a+2,a+4,……
設第一個數是a,得到第2個奇數a+2,第三個奇數a+4。
如果已知有4個或5個……連續的數的和,用上面的方法能快速地求出這些數嗎?
學生選擇方法嘗試。
問題:已知連續4個自然數的和為134,這幾個數分別是多少?
1.這4個數是相鄰、連續的;
2.相鄰兩個數的差值是“1”;
3.采用設未知數法,設第一個數為“a”,后面三個數依次為:a+1,a+2,a+3
4.它們之間相加的和:a+(a+1)+(a+2)+(a+3)=134
根據問題分析可以得出:
1.在“數據”類里新建一個全局變量“a”來表示第一個未知數;
2.在“a+(a+1)+(a+2)+(a+3)=134”中要用到“運算”邏輯運算符

3.這4個數相加的和為“134”,也就是當程序運行后,不斷地循環執行判斷,當有4個數相加的和為“134”時,程序跳出循環體,顯示程序執行結果,所以應該運用:

4.“重復執行直到”中的條件就是:

a+(a+1)+(a+2)+(a+3)=134,要依此條件搭建;其中循環條件是:讓程序重復執行多次后直到滿足和為“134”這一條件;
5.程序執行結束后,顯示結果:

在“新建對話框”中的內容應該是這4個數,數與數之間用“;”號隔開,即:

1.設置舞臺背景圖片,添加角色。
2.新建變量“a”,依次搭建4個數。
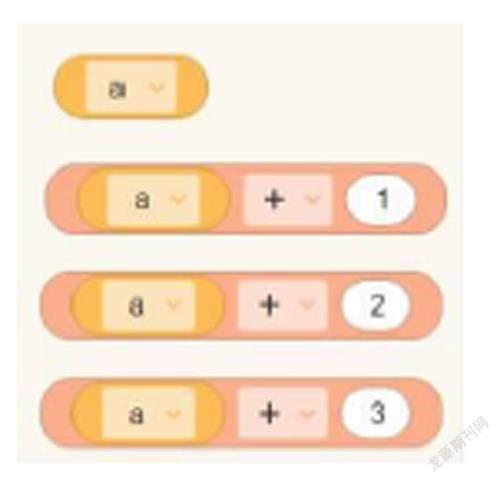
3. 搭建程序(如下圖)。

4.設置“等待0.1”秒是為了看到程序不斷重復執行的過程。
5.顯示程序運行結果時,在“新建對話框”中把4個數放在一起并用“;”號隔開,便于觀察。
本教學案例讓學生在解決同一類型問題的過程中體驗到了數學和編程解題不同的思路、方法。在“分析問題—編程思路—編程實現—程序執行”的編程中學會將問題化繁就簡,充分認識 “重復執行”“重復執行()次”的區別,理解和解決了“重復執行直到<>”這一教學難點,如“庖丁解牛”般將問題分解,建構模式,找出解決方案,初步培養了小學生編程中的計算思維。

