基于遺傳算法的衛星干擾源定位構型優化方法
柏如龍,施健康,霍立寰,陳 兵,黃鵬輝,陳建峰
(1.中國電子科技集團公司第五十四研究所,河北 石家莊 050081;2.河北省電磁頻譜認知與管控重點實驗室,河北 石家莊 050081;3.中國人民解放軍32027部隊,河南 開封 475000;4.上海交通大學 電子信息與電氣工程學院,上海 200240)
0 引言
近年來,衛星通信業務快速發展,已廣泛應用于電視轉播、通信廣播、導航定位、氣象預報、資源探測等多個領域。隨著衛星通信業務的迅猛發展以及新技術的出現,衛星所處的電磁環境日益惡化,且容易受到其他衛星和地面輻射源的干擾,對衛星電視、衛星通信等業務帶來較大影響[1-3]。輻射源位置是無線電信號重要的技術參數,高軌衛星干擾源定位具有覆蓋范圍廣、性能穩定的優勢,是無線電頻譜監測的重要手段,對衛星通信業務的正常開展、衛星廣播電視節目的安全播出具有重要意義[4-5]。
現有的干擾源定位技術以雙星時頻差、多星時差方法為主[6-9]。相比于雙星時頻差定位方法,多星時差定位能夠適用于運動目標,并且對星歷誤差的要求不高。多星時差定位方法主要受到時差測量精度、參考站位置和衛星定位構型有關,其中衛星定位構型是影響定位效果的主要因素。目前在衛星干擾源定位領域,學者們集中于時頻差測量、定位算法等問題上,在定位構型方面,僅僅考慮了基于典型構型的定位誤差分析,而鮮有對定位構型進行設計和優化的研究[10-15]。
針對上述問題,本文提出了基于遺傳算法的衛星干擾源定位軌位設計方法。首先基于衛星干擾源定位原理,推導了衛星定位的幾何稀釋度(GDOP)計算方法,然后針對衛星干擾源定位設計了遺傳算法中的軌道設計編碼、基于排序的適應度分配、輪盤賭選擇、精英保留策略等遺傳流程。該方法能夠快速地獲得干擾源定位構型結果,算法仿真和實星星歷仿真驗證了優選結果為在給定條件下的最優構型。
1 衛星定位GDOP計算模型
如圖1所示,一顆主星與兩顆鄰星構成了干擾源定位系統,當干擾源目標朝向主星發射干擾信號時,旁瓣的能量泄露到兩顆鄰星上。
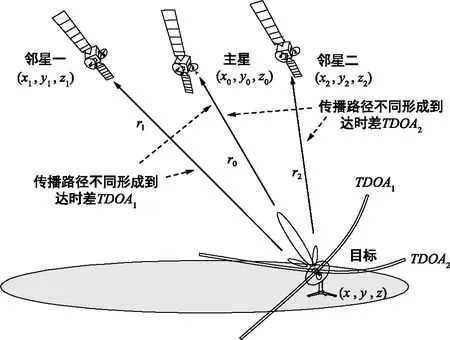
圖1 衛星干擾源定位幾何示意Fig.1 Configuration of thesatellite interference source location
受衛星定位構型、目標地理位置等因素的影響,目標到各個衛星的傳播路徑長度存在差異。通過時頻差測量技術能夠獲得主鄰星的時頻差,設目標與主星和鄰星一的到達時差為TDOA1,目標與主星和鄰星二的到達時差為TDOA2。根據主鄰星時差和衛星軌道位置,利用多星定位算法能夠反演出目標的地理位置。因此,目標的定位精度主要與主鄰星時差的測量精度和衛星定位構型有關。
設目標位置坐標為(x,y,z),主星位置坐標為(x0,y0,z0),鄰星一的位置坐標為(x1,y1,z1),鄰星二的位置坐標為(x2,y2,z2),則衛星時差定位的方程如下:
(1)
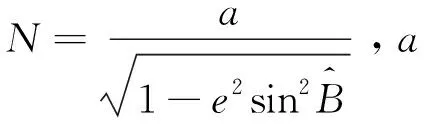
利用高斯迭代等方法能夠對多星時差定位方程進行求解,從而獲得目標位置。從衛星時差定位方程可以看出,目標定位精度主要受到星歷誤差、時差測量誤差、目標位置等因素的影響。為了更好地掌握多星定位性能,需要開展定位誤差分析。
對式(1)中的時差方程取微分,可得:
dr10=dr1-dr0=
(2)
令:
(3)
得到:
dr10=F1xdx+F1ydy+F1zdz-F1xdxl-F1ydyl-F1zdzl-
(F0xdx+F0ydy+F0zdz-F0xdx0-F0ydy0-F0zdz0)=
(F1x-F0x)dx+(F1y-F0y)dy+(F1z-F0z)dz+(K0-K1),
(4)
其中,
K1=F1xdx1+F1ydy1+F1zdz1(l=0,1,2)。
(5)
對式(1)中的地球橢球方程取微分,可得:
(6)
將式(4)和式(6)表示成矩陣形式,得到:
(7)
表示成矢量形式為:
DΔr=F·Dr+Ds,
(8)
其中,DΔr,Dr,Ds,F分別為時差測量誤差、目標定位誤差、星歷誤差、目標與衛星的幾何關系。具體含義如下:
(9)
(10)
(11)
(12)
由偽逆法可得,定位誤差估計值為:
Dr=C(DΔr-Ds),
(13)
其中,
C=(FTF)-1FT,
(14)
可以看出各個時差的測量中,都含有星歷測量的信息,導致每個時間差測量值都有相同的誤差因素,所以說在各處的測量誤差中,它們是相關連的。假定經系統修正后,測量誤差是零均值;接收機的位置誤差不變(每次的測量中);接收機的位置誤差與它們誤差各元素之間不相關,那么定位誤差的協方差可以表示為:
Pdr=C{cov(DΔr)}CT=
C{cov(DΔr)}CT。
(15)
由定義可得:
(16)
可得:
Pdr=C{cov(DΔr)}CT=
(17)
定位精度的幾何稀釋度為:
(18)
2 基于遺傳算法的軌位設計方法
衛星定位的定位精度受定位構型的影響較大,而衛星發射和變軌的代價巨大,提前進行衛星干擾源定位的軌道設計具有重要意義。衛星干擾源定位的軌道優選屬于一類復雜的非線性問題,尚未有有效的求解方法。枚舉類的搜索算法從理論上能夠遍歷搜索得到最優的定位軌位,然而計算量代價巨大。遺傳算法是一種借鑒進化機制和選擇機制的智能搜索算法,在對需解決的問題進行對應的遺傳算法建模后,能夠較好地解決非線性優化問題[16-19]。在基于遺傳算法的衛星定位軌位設計中,基于二進制編碼方法將衛星軌位映射到二進制編碼字符串上,通過建立多個個體組成的種群,基于定位誤差GDOP計算適應度函數,利用單點交叉和變異操作,采取精英保留策略,經過一定的遺傳代數收斂得到軌位設計結果。
結合遺傳算法和衛星干擾源定位方法,設計出基于遺傳算法的衛星軌位設計方法,算法流程圖如圖2所示。
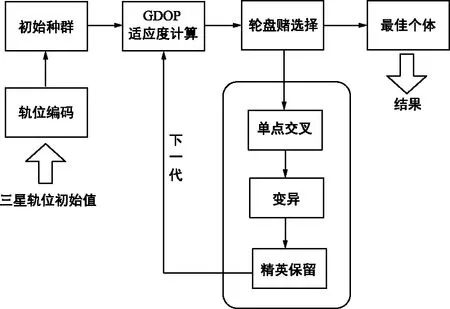
圖2 基于遺傳算法的定位構型優化流程圖Fig.2 Diagram of location configuration optimization method based on genetic algorithm
2.1 軌位設計編碼
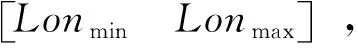
(19)
種群中單個個體由3顆衛星構成,則單個個體的二進制編碼表示為b=(b1b2b3)。
2.2 基于GDOP排序的適應度計算
為了避免適應度差距過大,而過早收斂,采用基于排序的適應度計算方法。適應度取決于個體在種群中的序號,而不是實際的代價函數值。個體的排序根據衛星定位構型的GDOP值進行排序,GDOP值越小,則排序的位置越靠前。設定M為種群大小,線性排序的適應度計算公式為:
(20)
其中,1≤η+≤2,η-=2-η+。
2.3 輪盤賭選擇
輪盤賭選擇方法類似于博彩游戲中的輪盤賭,個體適應度按比例轉化為選中概率。將輪盤分成10個扇區,因為要進行10次選擇,所以產生10個[0,1]之間的隨機數,相當于轉動10次輪盤,獲得10次轉盤停止時指針位置,指針停止在某一扇區,該扇區代表的個體即被選中。
2.4 交叉和變異
在種群中任意挑選經過選擇操作后種群中兩個個體作為交叉對象,即兩個父個體經過染色體交換重組產生兩個子個體,通過隨機產生一個交叉點位置,父個體1和父個體2在交叉點位置之右的部分基因碼互換,形成子個體1和子個體2。類似地完成其他個體的交叉操作。
效法自然界生物變異。生物性狀的變異上控制該性狀的基因碼發生了突變,這對于保持生物多樣性是非常重要的。模仿生物變異的遺傳操作,對于二進制的基因碼組成的個體種群,實現基因碼的小概率翻轉,即達到變異的目的。
2.5 精英保留策略
精英保留策略可以避免最優個體不會因為雜交操作而被破壞,即在每一代中保留上一代產生的最優個體。設到第t代時,群體中A(t)為最優個體。經過輪盤賭選擇、交叉和變異操作后,生成了第t+1代群體。在第t+1代群體中,將排序最后的個體替換成為上一代的最優個體A(t)。這樣,既保持群體的規模不變,又能將進化過程中生成的最優個體一直保留。
3 仿真實驗
3.1 算法有效性試驗
在實際的衛星干擾源定位中,往往需要定位某個區域的目標。因此,在仿真試驗設計中,定位區域劃分為某個區域。設目標區域中心位置為115.84°E,28.67°N,經緯度所需覆蓋范圍各為20°。3顆衛星軌道的中心位置分別為85.5°,110.0°,125.0°,衛星軌道窗口分別為5°,10°,7°。遺傳算法個體的基因總數為17,交叉概率為0.4,變異概率為0.2,代數為100。表1給出了衛星軌位隨遺傳代數的變化情況,可以發現,當世代數為50時即達到了收斂,此時衛星軌位為83.09°,105.02°,128.50°,平均誤差為41.39 km。圖3(a)給出了隨著遺傳代數,平均定位誤差的變化情況,圖3(b)給出了優化軌位后的GDOP圖。圖3(c)給出了常用構型1(85.5°,110.0°,125.0°)的GDOP圖,圖3(d)給出了常用構型2(83°,110.0°,128.5°)的GDOP圖,可以發現,所提方法能夠獲得優于其他常用定位構型的定位誤差結果。
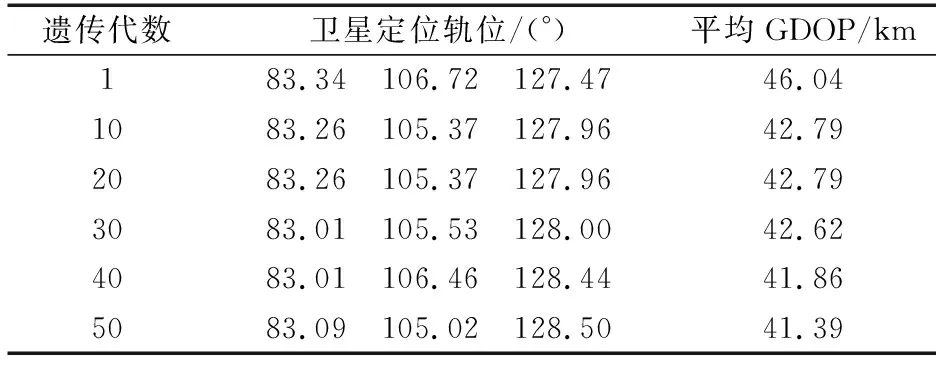
表1 衛星定位軌位隨遺傳算法世代數變化Tab.1 Variation of the satellite orbital position with genetic algorithm generation
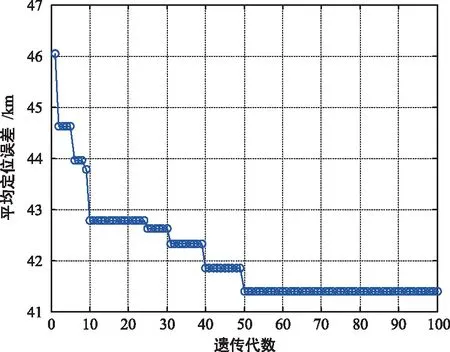
(a) 定位誤差隨遺傳代數變化情況

(b) 所提方法定位誤差分布情況
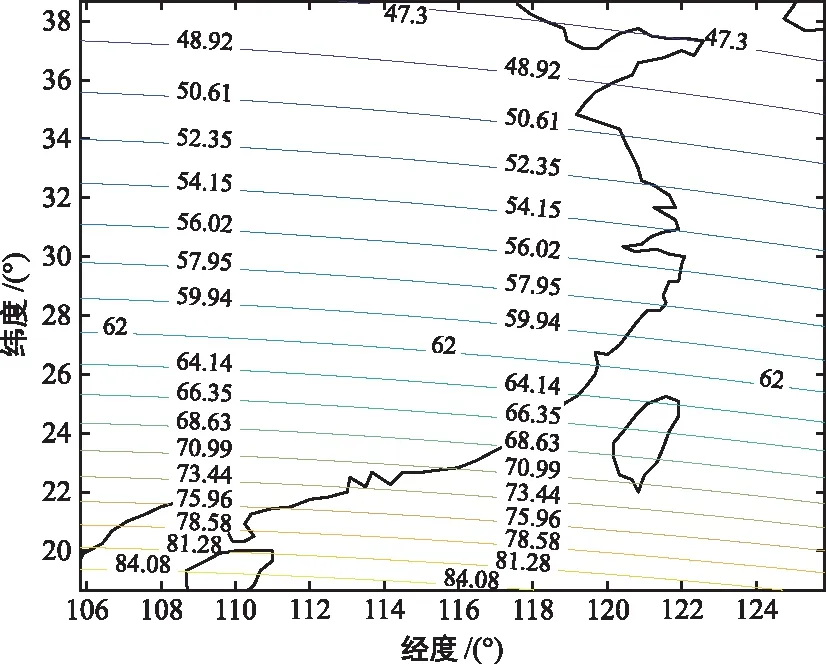
(c) 常用構型1定位誤差分布
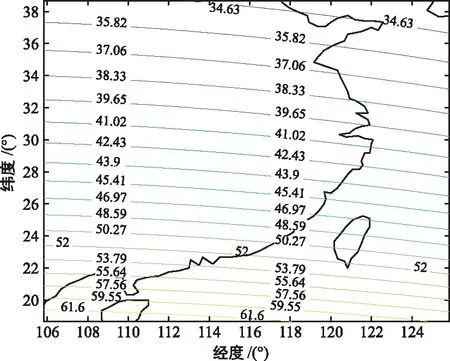
(d) 常用構型2定位誤差分布
3.2 實星星歷仿真驗證
設目標區域中心位置為108.94°E,34.33°N,3顆衛星軌道范圍為85°~135°。遺傳算法個體的基因總數為17,交叉概率為0.4,變異概率為0.2,代數為100。表2給出了衛星定位構型隨遺傳代數的變化情況,可以發現,當世代數為60時即達到了收斂,此時衛星定位軌位為85.41°,110.37°,134.75°,平均誤差為29.52 km。圖4(a)給出區域平均GDOP誤差隨遺傳代數的變化情況,圖4(b)給出了優化軌位后的GDOP圖。圖5給出了實星構型的仿真情況。根據遺傳算法的軌位設計結果,主星選擇軌位87.5°的CHINASAT 12,鄰星一選擇軌位132°的VINASAT-1,鄰星三則在主星和鄰星一中間依次選擇了10顆不同軌位的衛星。衛星兩行星歷日期為2020年4月16日,基于SGP4算法生成衛星星歷。通過圖5可以發現,衛星軌位約為110°時能夠獲得最優的GDOP值,這與遺傳算法的搜索結果一致。
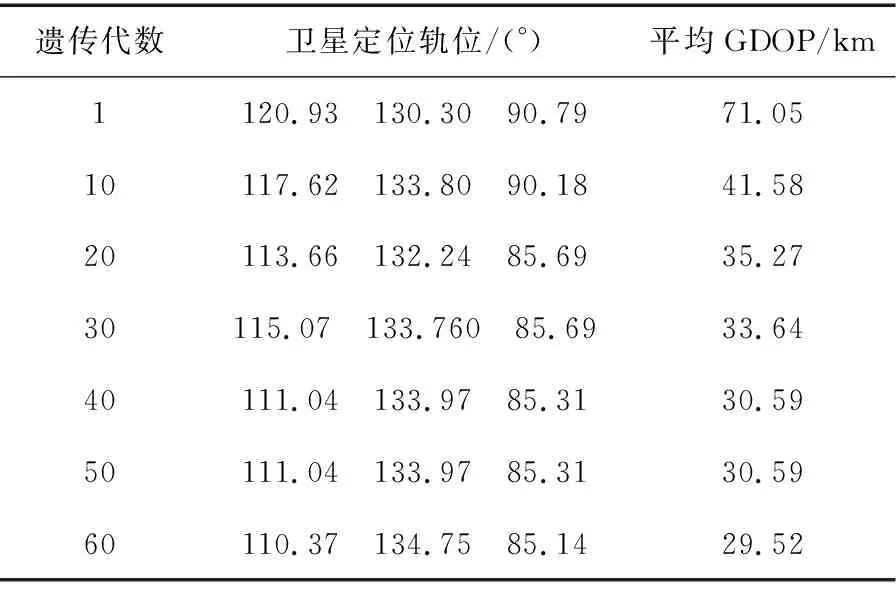
表2 實星定位軌位隨遺傳算法世代數變化Tab.2 Variation of the real satellite orbital position with genetic algorithm generation
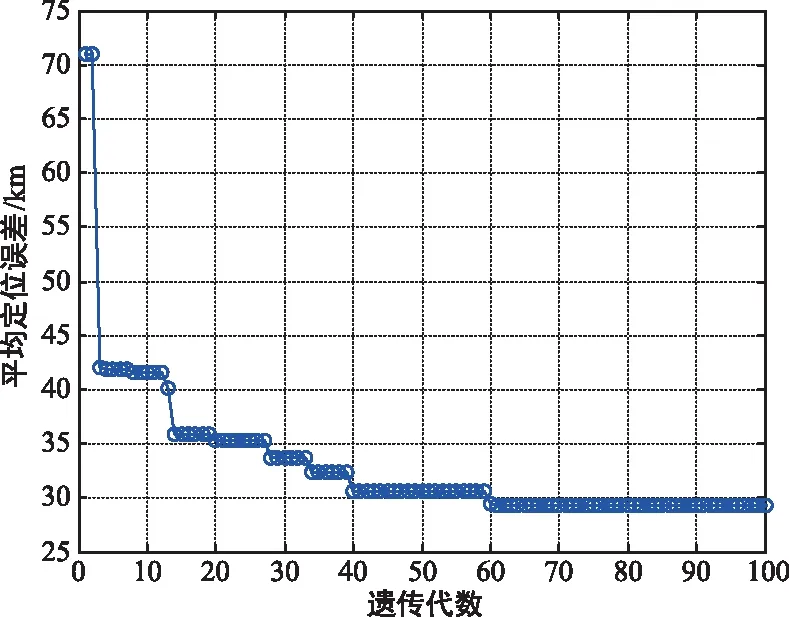
(a) 定位誤差隨遺傳代數變化情況
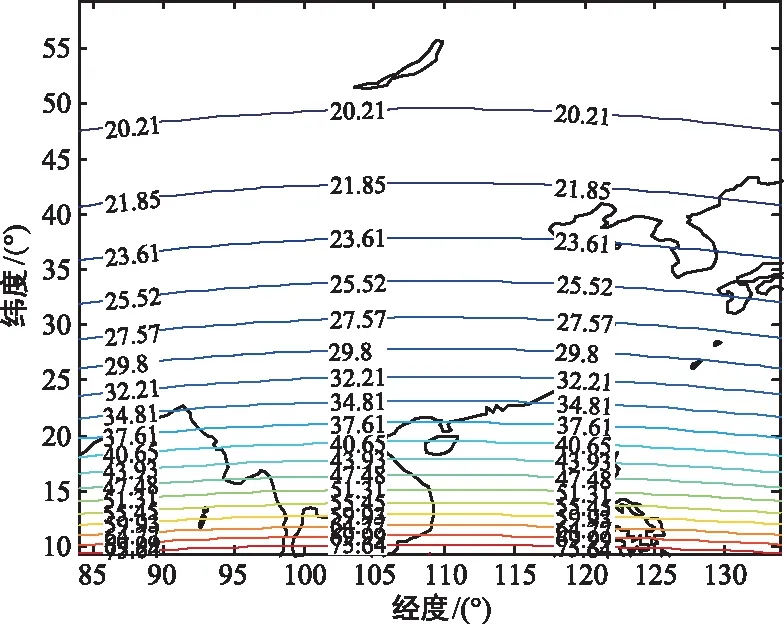
(b) 定位誤差分布情況圖4 實星定位構型優化結果Fig.4 Location error results of the optimization for real satellites
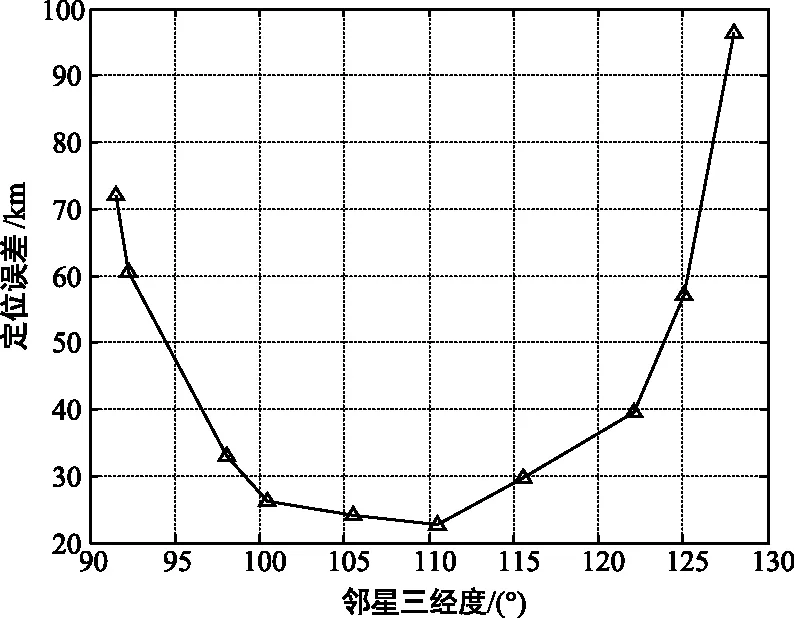
圖5 定位誤差隨鄰星三經度的變換情況Fig.5 Variation of location error with the longitude of adjacent satellite 3
4 結束語
衛星定位精度與定位構型有直接聯系,而在軌的衛星受到燃料、動力等因素的制約,幾乎難以大幅調整位置。因此,提前進行衛星定位的軌道優選尤為重要。鑒于傳統構型設計方法的計算量巨大,本文基于智能類算法中的遺傳算法,探索了基于遺傳算法的衛星定位構型設計方法。仿真實驗表明本文方法對單目標、區域目標等定位場景均能夠收斂到最優的定位構型,并結合實星星歷,驗證了所提方法能夠對實際工程應用提供重要參考。

