不同側壓系數下矩形巷道逐步開挖的穩定性分析

栗東平，馮瑞廣

（1.河北工程大學 土木工程學院，河北 邯鄲 056038；2.河北工程大學 計算力學與工程應用研究中心，河北 邯鄲 056038）

深部煤層處于高地應力、高地溫、高孔隙水壓力的地質環境。因為對深部巷道圍巖的力學特性認識不夠充分，不能制定合理的巷道圍巖支護措施，導致層裂、巖爆、設備損壞和生產受阻等問題頻頻發生[1-4]。目前，許多學者對深部巷道圍巖的穩定性進行了大量的研究。如：郭建卿等[5]通過FLAC3D軟件建模分析側壓力系數對巷道變形及周邊應力分布的影響規律；林志斌等[6]基于深埋圓形巷道工程的研究，得出了巖體總裂紋數與側壓力系數呈拋物線關系；范磊等[7]基于Mohr-Coulomb 和Drucker-Prager 強度準則，并采用數值模擬軟件分析得出：隨著側壓力系數的變化，圍巖應力的分布狀態基本不變；龍翼等[8]采用試驗與數值模擬相結合的方法，對不同地應力場下爆破擾動誘發巷道破裂現象進行研究，得出了地應力場控制圍巖破壞特征，爆破擾動加劇圍巖破壞速度的結論；董春亮等[9]、王新豐等[10-11]基于數值模擬、層次分析及相似模擬試驗等方法，得出了深部開挖巷道圍巖變形破壞特征；王學濱等[12-14]基于三維非均質模型對巷道圍巖進行研究，得出不同軸壓比、內摩擦角對分區破裂化的影響規律；Chen 等[15]、Wei等[16]根據現場實測資料建立顆粒流模型，研究了側壓力對巷道圍巖穩定性的影響規律及圍巖的變形損傷特征和機理；Yu 等[17]、Meng 等[18]通過數值模擬，研究了深部巷道的應力、位移、和塑性區分布的演化規律。上述研究成果表明，深部巖體地應力場對巷道圍巖的破壞特征的研究，有助于煤層深部開采圍巖穩定性分析及安全控制措施的提出。巷道開挖擾動是圍巖變形和破壞的主要因素，目前對巷道逐步開挖和不同側壓力對圍巖穩定性的研究較少，巷道逐步開挖對圍巖穩定性的影響機理有待于進一步研究。為此，根據某礦實際資料建立數值模型，采用快速應力邊界法建立初始應力場[19]，之后進行巷道逐步開挖分析，并與相似模擬試驗[20]結果進行對比分析，驗證數值模型的可行性；最后通過修改模型的側壓力系數，對不同側壓系數下巷道逐步開挖塑性區和主應力差的演化規律進行研究。

1 數值模型的建立

1.1 參數選取

根據某礦軌道下山巖層數據確定深部巷道開挖模型參數[20]。建立數值模型尺寸為長（x 方向）×寬（y方向）×高（z 方向）：50 m×50 m×47 m。模型共被離散為82 000 個單元和87 822 個節點。初始邊界條件為xoz 平面、yoz 平面和xoy 平面的下表面采用速度約束（固定速度為0 m/s），上邊界為自由平面。在模型上邊界處添加上覆巖層的自重應力，約為25.23 MPa。模型本構關系選為Mohr-Coulomb 強度準則，數值模型如圖1。巷道形狀為矩形，截面尺寸寬（x 方向）×高（z 方向）：5 m×4 m。巖層物理力學參數見表1。

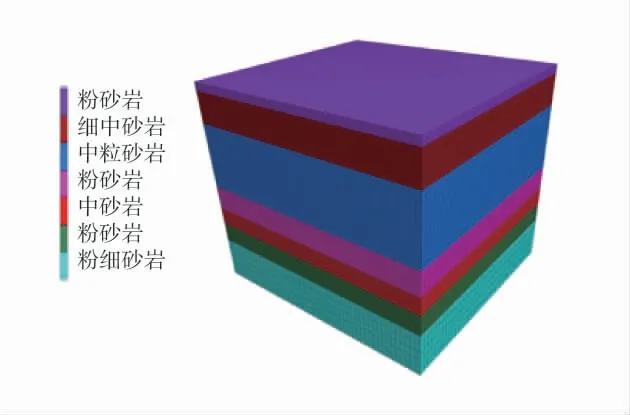
圖1 數值模型Fig.1 Numerical model

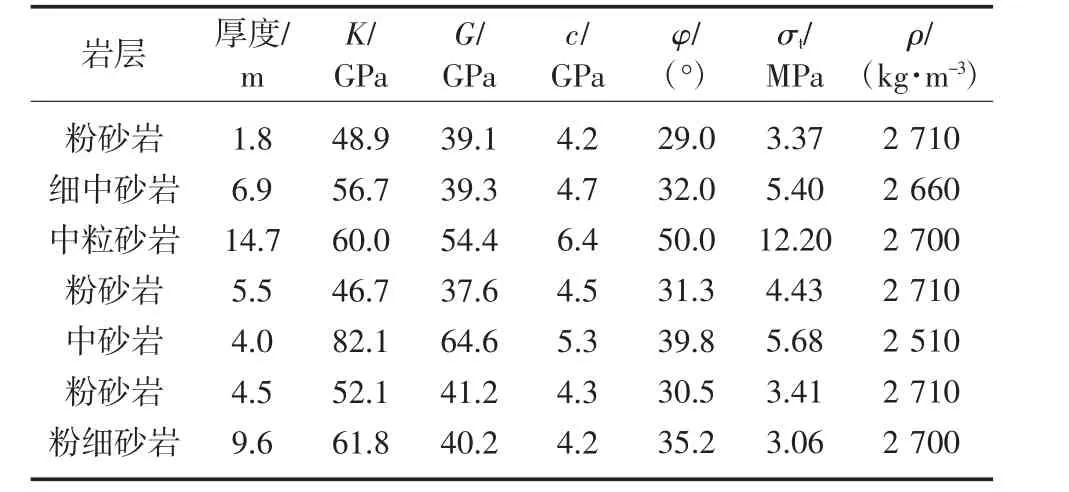
表1 巖層物理力學參數Table 1 Physical and mechanical parameters of rock strata

1.2 模擬方案

考慮到模型具有對稱的特點，只對巷道的一側進行監測。因此在模型y=25 m 平面上布置測點，主要布置點在巷道頂板、幫部和底板，各測線監測點間距1 m，測點布置如圖2。計算過程分為2 步。

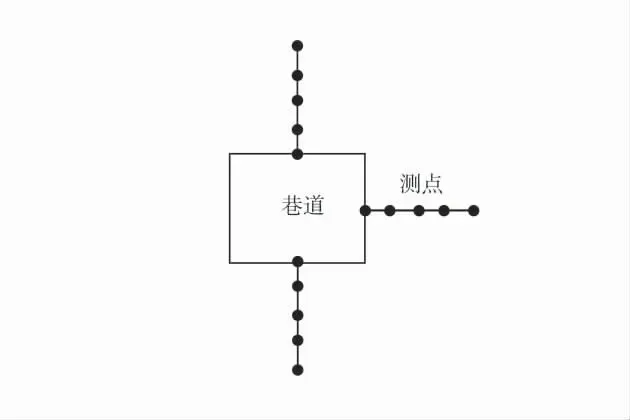
圖2 測點布置圖Fig.2 Layout of measuring points

1）根據實測數據建立模型并劃分網格，對不同巖層進行賦值，采用S-B 法生成初始地應力場。

2）將模型初始速度、初始位移設置為0，對模型xoy 下邊界、xoz 邊界和yoz 邊界添加速度約束，之后對巷道進行逐步開挖，每步開挖5 m，共計開挖10步，其中每2 次開挖間隔進行1 次靜力平衡。

開挖10 次之后，形成貫穿模型的巷道。

模型計算中共采取5 個計算方案，側壓力系數分別取值為0.5、0.8、1.1、1.4、1.7，其他參數取值相同。

2 計算結果驗證

文獻［13］進行了相似模擬試驗，試驗原型為某礦軌道下山，巷道埋深1 000 m，掘進斷面為高4 m寬5 m 的矩形截面，模型上邊界處施加25.23 MPa的垂直應力，水平邊界處施加27.75 MPa 的水平應力，其他條件詳見上文參數。為與試驗結果進行對比驗證，在模型中依據試驗測點位置，等比例布置監測點。數值模擬結果與文獻中試驗結果數據對比見表2 和表3。

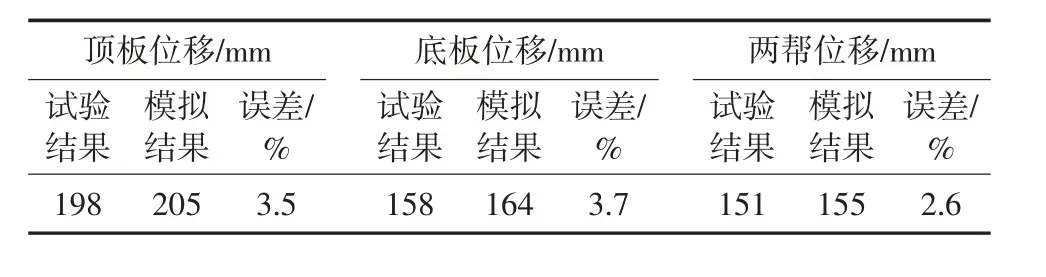
表2 最大位移對比Table 2 Comparison of maximum displacement

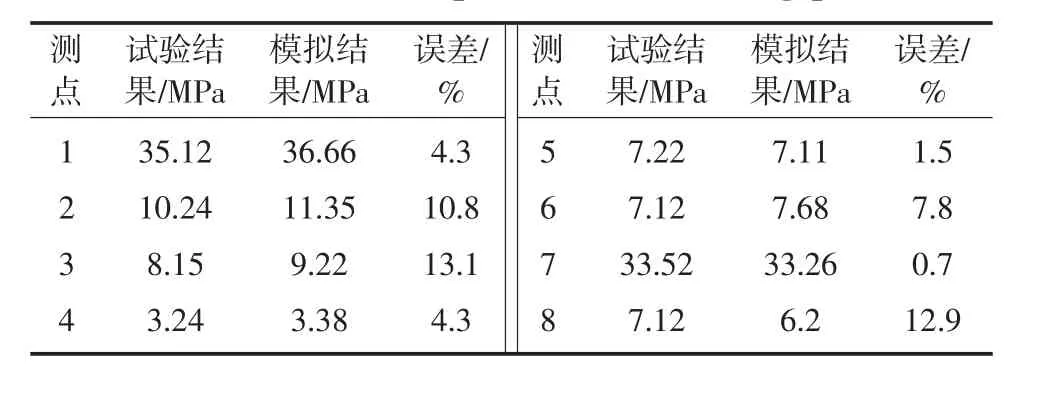
表3 部分測點應力對比Table 3 Stress comparison of measuring points

由表2 可以發現，數值模擬結果比試驗結果大，最大誤差為3.7%。這是由于數值模擬中邊界條件、施加應力方式及材料屬性與試驗不同。如在建模過程中，通常對邊界條件和巖層力學參數進行簡化，實際巖層為近水平巖層，模擬中簡化為水平巖層進行研究，進而對數值分析結果造成一定誤差。

由表3 可以看出，各測點試驗與模擬得出的應力值基本接近，部分數據存在一定的誤差。這是由于快速應力邊界法生成的水平應力場比實測數據的水平應力大，垂直應力場與實測數據相接近[21]。綜上所述，說明模擬得到的結果和試驗結果基本吻合，數值模擬具有可行性。

3 計算結果及分析

3.1 方案1 結果分析

3.1.1 主應力差分析

巷道逐步開挖監測點主應力差演化圖如圖3。

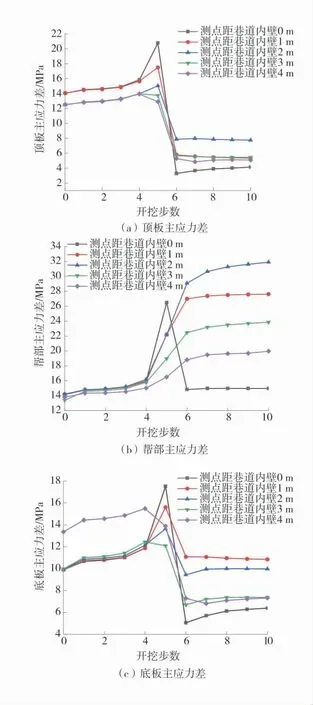
圖3 巷道逐步開挖監測點主應力差演化圖Fig.3 Evolution diagrams of principal stress difference at monitoring points of roadway excavation step by step

由圖3 可知，開挖第4～第6 步時，圍巖主應力差值變化幅度較大，第5 步開挖時開挖面位于測點監測面，表明距開挖面5 m 范圍內（每步開挖5 m）部分圍巖發生變形破壞，導致承載強度及剪切強度降低，部分應力開始向巖體深部轉移。隨著測點距巷道內壁距離的增加，主應力差值呈先快速增加后減小的變化趨勢，且變化趨勢不受開挖步數的影響，表明圍巖應力重分布不受巷道開挖步數的影響。

由圖3（a）、圖3（c）可知，頂板和底板主應力差隨著巷道開挖步數的增加，呈先緩慢增加至最高點，之后快速減小并趨于穩定的變化趨勢。在第1 步開挖后，主應力差值緩慢增加；在第5 步開挖后，頂板距巷道內壁1 m 處測點的主應力差值達到最大值20.78 MPa，底板距巷道內壁1 m 處主應力差值達到最大值17.53 MPa，表明巷道開挖導致部分巖體發生應力重分布現象，應力向巖體深處轉移，但此時圍巖抗剪強度大于剪應力，巖體沒有發生破壞。第5 步開挖后，主應力差值快速減小，表明此時圍巖發生破壞，抗剪強度顯著減小；第6 步開挖后，主應力差值趨于穩定，表明此時圍巖受開挖步數的影響程度逐漸減小，巖體停止破壞，并形成了新的承載結構，應力重分布現象停止，在之后的開挖過程中圍巖將保持著較好的穩定性。

由圖3（b）可知，幫部主應力差隨巷道開挖步數的增加呈現緩慢、快速、緩慢增加至最高點并趨于穩定的變化趨勢。表明巖體出現應力向深部轉移的現象，且巷道圍巖未發生失穩現象，有較好的穩定性。

3.1.2 塑性區分析

y=25 m 平面巷道逐步開挖塑性區演化如圖4。

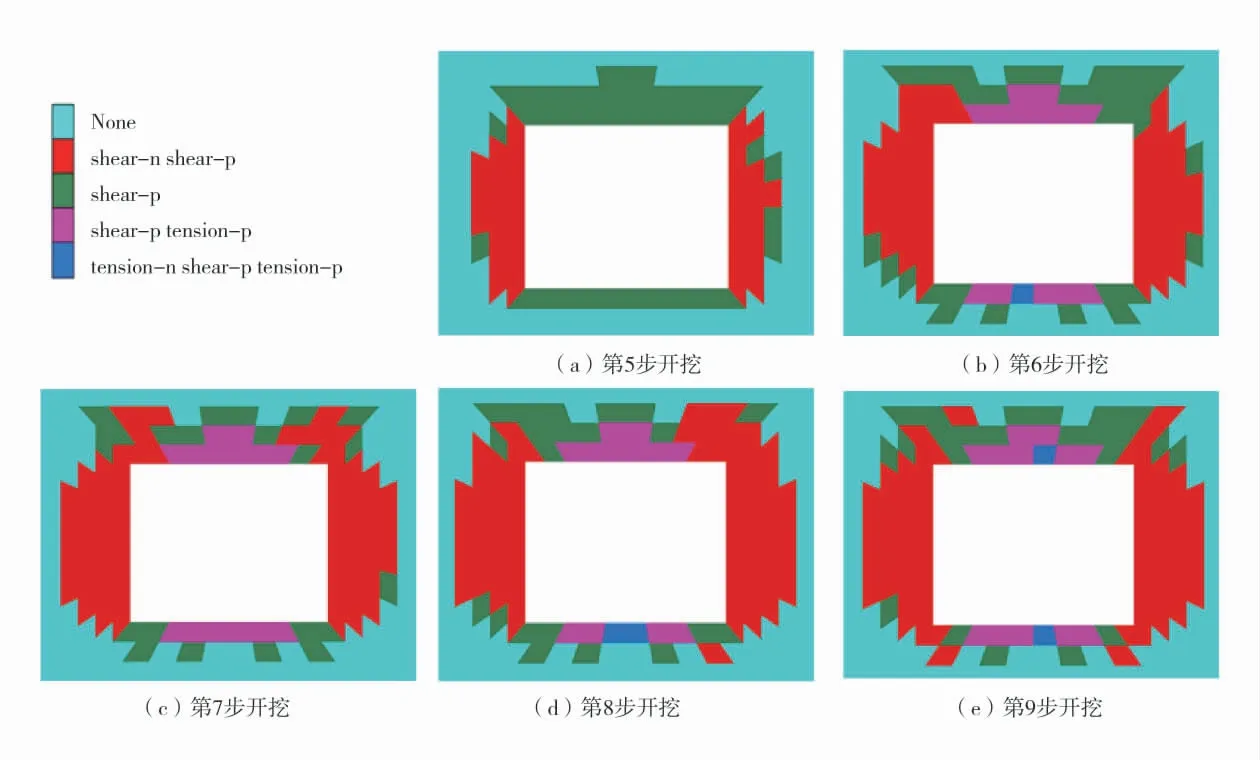
圖4 y=25 m 平面巷道逐步開挖塑性區演化Fig.4 Evolution of plastic zone of roadway excavated in y=25 m plane

由圖4 可知，當巷道在第5 步（即y=25 m 剖面處）開挖時，塑性區分布范圍最小，頂板和兩幫破壞深度為1.5 m，底板破壞深度為0.5 m，當開挖第6步時，塑性區分布面積增加，頂板破壞深度為1.5 m，兩幫破壞深度為1.8 m，底板破壞深度為1 m，當開挖第7～第9 步時，塑性區分布范圍不變，表明巷道走向圍巖距離開挖面0～5 m 時（即開挖第5～第6步），對巷道圍巖破壞深度影響程度從大到小排序為底板、兩幫、頂板，對巷道圍巖破壞分布范圍影響程度從大到小排序為兩幫、底板、頂板，巷道走向圍巖距離開挖面大于5 m 時（即開挖第6～第10 步），圍巖破壞深度和破壞分布范圍幾乎不受影響。隨著巷道開挖步數的增加，兩幫圍巖正在剪切破壞分布范圍趨勢為增加、緩慢增加并趨于穩定，頂板圍巖正在剪切破壞分布范圍為先增加后減小，表明巷道走向圍巖對距離開挖面小于0～5 m 處圍巖影響程度較大，對距離開挖面5～15 m 處圍巖影響程度較小，對距離開挖面大于15 m 處圍巖影響程度可忽略不計。當巷道開挖步數大于第6 步時，巷道頂板和底板出現曾拉伸破壞，并且圍巖曾拉伸破壞分布范圍不變，表明巷道圍巖隨著開挖步數的增加，圍巖變形破壞程度不斷增加，巷道內壁圍巖殘余強度不斷減小，導致圍巖殘余抗拉強度小于拉應力，圍巖發生拉伸破壞；開挖步數為第6、第8、第9 步時，巷道底板和頂板部分區域出現正在拉伸破壞，開挖步數為第7步時，頂板和底板圍巖正在拉伸破壞分布范圍為0，表明隨著巷道的開挖，巷道內壁的頂板和底板中部圍巖不斷進行拉伸破壞-穩定的循環，且開挖步數對底板圍巖變形破壞的影響程度大于對頂板圍巖變形破壞的影響程度。

3.2 不同方案結果對比分析

3.2.1 不同側壓系數主應力差對比分析

y=25 m 平面巷道在不同側壓系數主應力差演化如圖5。

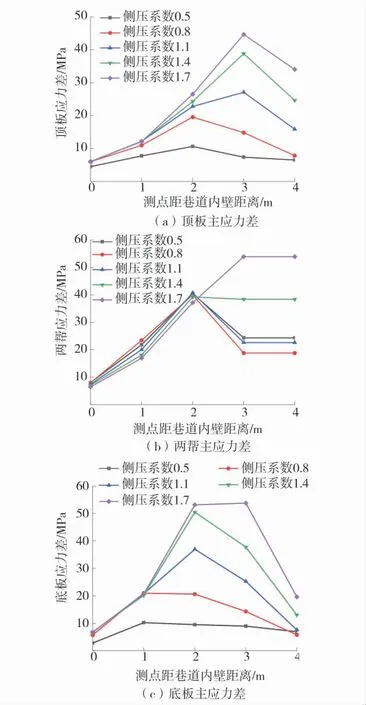
圖5 y=25 m 平面巷道在不同側壓力下主應力差演化Fig.5 Evolution of principal stress difference in y=25 m plane roadway under different lateral pressures

由圖5 可知，圍巖主應力差值隨著距巷道內壁距離的增加，呈先增加至最高點，再減小的變化趨勢。兩幫在距巷道內壁深2 m 處主應力差值達到最大值，頂板在距巷道內壁深3 m 處主應力差值達到最大值，底板在距巷道內壁深4 m 處主應力差值達到最大值；當巷道圍巖主應力差值增長時，如頂板圍巖距巷道內壁深1～3 m 范圍內，主應力差值隨距離巷道內壁距離增加，表明巷道圍巖1～3 m 深處圍巖發生變形破壞程度越高，圍巖殘余承載強度越低，向內部深處轉移的應力越多；當圍巖主應力差值達到最大值時，如頂板圍巖深3 m 處，表明應力轉移進入深部圍巖后，圍巖變形破壞承受剪切力較低，圍巖形成了新的穩定狀態；當圍巖主應力差值減小時，如頂板圍巖距巷道內壁深3～4 m 范圍內，表明巷道內壁處圍巖應力基本轉移在圍巖深3 m 處，3 m 以上深處圍巖因巷道開挖導致的應力轉移現象較少。

由圖5（a）和圖5（c）可知，主應力差值變化趨勢為：當側壓力系數小于1.1 時，主應力差變化幅度增加，當側壓力系數大于1.1 時，主應力差變化幅度減小。圍巖主應力差值峰值點，隨著側壓力系數的增加，頂板的變化幅度大于底板的變化幅度，表明側壓力對頂板圍巖的影響較大，在后期巷道支護中應注意圍巖1 m 深范圍內圍巖的穩定，其中頂板的穩定性是關注的重點。由圖5（b）可知，距巷道內壁深度0～2 m 處，兩幫主應力差值基本無變化，表明該范圍內圍巖發生剪應力破壞，主應力差值受圍巖殘余抗剪強度及承載能力影響。距巷道內壁深度2～4 m處，主應力差值趨于穩定，且隨著側壓力系數的增大而增大，表明圍巖穩定性良好，受剪切破壞較低，因此側壓力對兩幫影響最小。

3.2.2 不同側壓系數塑性區對比分析

y=25 m 平面巷道在不同側壓系數下塑性區演化如圖6。

由圖6 可知，隨著側壓系數的增加，巷道圍巖塑性區破壞深度和破壞分布范圍基本不變，圍巖正在剪切破壞分布范圍呈緩慢增加、減小、增加的趨勢，頂板和底板圍巖主要為曾剪切破壞和曾拉伸破壞，底板中部圍巖正在拉伸破壞，兩幫圍巖主要發生正在剪切破壞和曾剪切破壞。

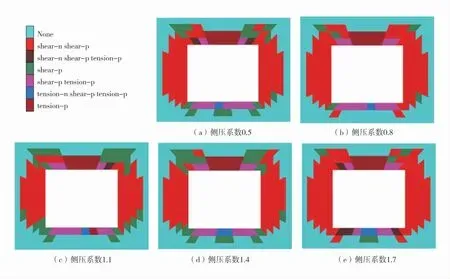
圖6 y=25 m 平面巷道在不同側壓系數下塑性區演化Fig.6 Plastic zone evolution of y=25 m plane roadway under different lateral pressure coefficients

頂板圍巖曾拉伸破壞分布范圍不變，正在剪切破壞分布范圍隨著側壓系數的增大呈增大、緩慢減小、快速增大的趨勢，表明隨著水平應力的增大，圍巖剪切強度和承載強度增加，但由于圍巖強度隨著側壓系數的增大呈非線性關系，在側壓系數較小時，圍巖剪切強度和承載強度增長較快，側壓系數較大時，圍巖剪切強度和承載強度增長較慢，因此側壓系數為0.5～0.8 時，圍巖強度快速增加，頂板剪切強度與剪切應力相差幅度越來越小，導致頂板正在剪切分布范圍緩慢增加，當側壓系數為0.8～1.4 時，剪切應力小于剪切強度，頂板增長剪切破壞分布范圍變小，當側壓系數為1.4～1.7 時，圍巖強度增加緩慢，由于肩部出現變形破壞，頂板穩定狀態受到影響，導致頂板正在剪切破壞增加。兩幫圍巖正在剪切破壞分布范圍隨著側壓系數的增大呈現緩慢減小，增大、緩慢增大的趨勢，表明當垂直應力小于剪切應力時，即側壓力系數小于1 時，圍巖剪切強度隨著圍壓的增大而增大，隨著側壓系數的增大，部分圍巖剪切強度大于剪切應力，正在剪切破壞分布范圍變小；當側壓系數大于1 時，巷道圍巖強度增加幅度小于剪切應力增加幅度，導致部分圍巖剪切強度小于剪切應力，兩幫正在剪切破壞分布范圍增大。底板圍巖主要由曾剪切破壞和曾拉伸破壞構成，隨著側壓系數的增大，底板中部圍巖拉伸破壞分布范圍逐漸增加，底腳正在剪切破壞范圍逐漸增加，表明側壓系數的增大時，底板中部圍巖由于圍壓過大導致巷道內壁中部圍壓拉應力增大，進而拉伸破壞分布范圍緩慢增加，由于底腳處圍巖剪切破壞分布范圍逐步增加，巷道開挖形成的圍巖穩定結構受到影響，導致底板變形破壞程度增加，進而圍巖殘余強度降低，部分圍巖承載強度小于拉壓應力，導致底板兩側出現拉伸破壞。

4 結 論

1）側壓力系數一定時，隨著巷道開挖步數的增加，頂板與底板主應力差呈先增加后減小并趨于穩定的變化趨勢，幫部主應力差呈先緩慢、快速、緩慢增加至最高點并趨于穩定的變化趨勢。

2）側壓力系數一定時，對距離巷道開挖面0～5 m 內圍巖塑性區分布的影響程度較大。隨著巷道開挖步數的增加，巷道圍巖出現剪切破壞，頂板和底板中部圍巖出現拉伸破壞。

3）隨著側壓力系數的增大，對巷道穩定性的影響程度依次為頂板、底板、兩幫，其中兩幫在不同側壓力下都表現為距巷道內壁深0～1 m 處圍巖先破裂后應力轉移向深處圍巖。

4）隨著側壓力系數的增大，巷道圍巖塑性區分布范圍和破壞深度基本不受影響；圍巖整體正在剪切破壞分布范圍呈緩慢增加、減小、增加的趨勢；底腳和肩部正在剪切破壞分布范圍呈先減小后增多趨勢；兩幫圍巖塑性區以正在剪切破壞為主，應在后期的支護和維修中重點關注。