0～2.36 mm再生細集料水泥穩定碎石相對濕度和干燥收縮性能

蘭雪江，張 翛，王永寶，郝忠卿，高 陽，董曉強

(太原理工大學 土木工程學院，太原 030024)

過去幾十年，我國低等級公路路面大量采用水泥混凝土材料，近年來道路重修產生了大量的廢棄混凝土路面板，將其破碎成再生集料可以以一定的比例替代天然集料用于水穩碎石基層[1]。然而，作為再生集料破碎過程的副產品，再生細集料的比例占50%[2]，且其比表面積大、吸水率和孔隙率高的特點導致性能遠低于再生粗集料。其中0～2.36 mm粒徑性能更差，使用有限，堆積量驚人[3]，0～2.36 mm再生細集料(若無特別說明，后文中RFA均代表0～2.36 mm再生細集料)的應用具有重要意義。

目前對再生細集料的研究主要集中在混凝土中，其干燥收縮作為一項重要的長期性能對混凝土構件正常使用階段具有重要影響。研究發現混凝土干縮應變隨再生細集料摻量的增加而增大，其中2.36～4.75 mm粒徑的影響極小[4-5]，而0～2.36 mm粒徑影響較大，使干縮增大90%以上[4]。水泥、集料、濕度等影響因素使混凝土產生內部毛細管壓力、表面張力和內部分離壓力，導致收縮過程變得復雜，為有效預測并評估其長期收縮性能，國內外研究人員進行了大量研究，得到了較多干縮預測模型，典型的有B3、CEB/FIP、ACI209和GL2000等[6-9]。水穩碎石是具有與混凝土類似性能的水泥基膠凝材料，其干燥收縮也受水泥和集料等因素的影響[10-12]，然而其干縮模型研究較少，且均未考慮RFA對收縮性能的影響。

混凝土內部水分的變化對其干燥收縮具有重要影響，內部濕度與干燥收縮之間具有較強的相關性，內部濕度顯著降低時，干燥收縮增大[13-14]。大量的研究人員通過FICK定律建立濕度模型，以此來預測混凝土內部濕度變化[15-17]，DING et al[18]、JIANG et al[13]、SHEN et al[19]分別引入水泥組成、水灰比、養護溫度等影響參數，對濕度模型進行了修正。同樣的，水穩碎石內部水分的變化對其干燥收縮也具有重要影響，然而其與混凝土濕度變化有一定差別，且現有模型尚未考慮RFA對水穩碎石濕度的影響，建立其濕度預測模型對研究其收縮性能具有重要意義。

因此，本課題對RFA水穩碎石(CSM-2.36RFA)的濕度和干燥收縮進行了長期的測量，建立了不同RFA摻量下的CSM-2.36RFA內部濕度理論預測模型，在參照GL2000模型的基礎上提出了CSM-2.36RFA的干燥收縮理論預測模型，并對兩者的關系進行了研究，為CSM-2.36RFA長期干燥收縮耐久性性能提供理論依據。

1 試驗材料和方法

1.1 試驗原材料

天然集料取自山西太原當地的石灰巖，將其篩分為4個粒徑范圍，其技術參數測試結果見表1，其中0～2.36 mm粒徑篩分曲線如圖1所示，經調查，該結果與太原當地大部分0～2.36 mm天然細集料級配相近。

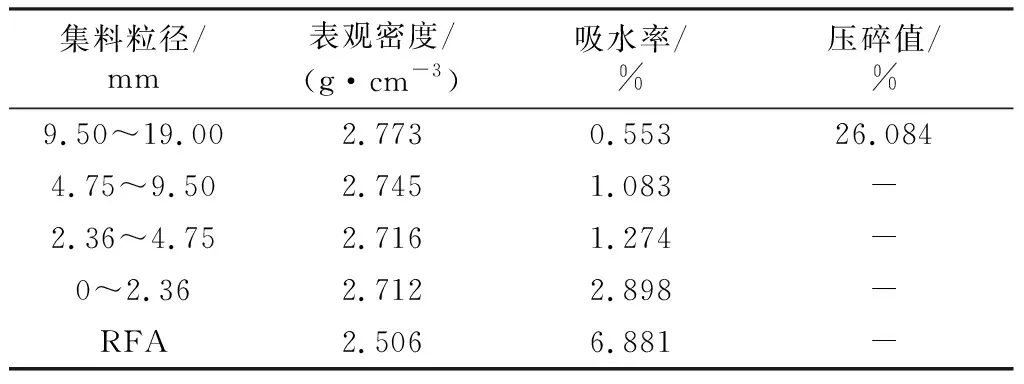
表1 集料技術參數Table 1 Technical parameters of aggregate

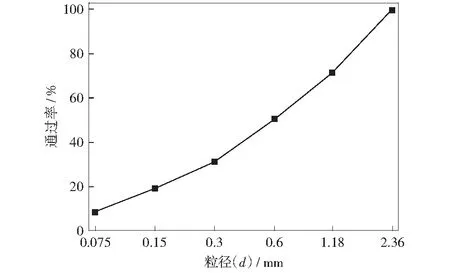
圖1 0～2.36 mm天然集料級配曲線Fig.1 Distribution curve of 0～2.36 mm natural aggregate

再生集料取自北京某路段廢棄混凝土路面板，粒徑約為10 mm，為模擬再生集料回收過程中副產品RFA的產生過程，使用錘式破碎機進行二次破碎。其技術參數見表1，RFA的表觀密度與0～2.36 mm粒徑的天然細集料相比低約7%，吸水率約高1.4倍，這是因為RFA的表面有大量的水泥漿和微裂紋。為排除因級配不同引起的結構性能差異，按0～2.36 mm天然細集料級配進行RFA配置。

試驗中采用太原獅頭水泥有限公司的普通硅酸鹽水泥P.O 42.5，試驗用水為太原市普通自來水。

1.2 配合比設計

根據《公路路面基層施工技術細則》(JTG/T F20-2015)[20]，經調查發現其中C-B-2級配在山西當地的工程中被廣泛使用，因此本課題選用C-B-2級配。水泥摻量(質量分數)選用4%、5%和6%，RFA摻量選用0、30%、60%和100%.通過重型擊實試驗確定CSM-2.36RFA的最佳含水量和最大干密度，進而確定其配合比[21]，如表2所示。

由表2可知，RFA摻量影響水穩再生碎石最佳含水量和最大干密度。隨著RFA摻量的增加，水穩碎石的最佳含水量增大，最大干密度減小。這是由于RFA吸水率大于天然細集料，而其表觀密度較小，使水穩再生碎石具有較大含水量和較小干密度。隨著水泥摻量的增加，最佳含水量和最大干密度均增大，且呈近似線性關系。

1.3 試驗方法

制備φ100 mm×100 mm的圓柱試樣進行無側限抗壓強度試驗，400 mm×100 mm×100 mm長方體試樣進行干燥收縮試驗，脫模后放置于溫度(20±1) ℃、相對濕度95%的條件進行標準養護。制備干縮試樣時，在頂部預留兩個直徑15 mm、深60 mm的圓柱孔，兩孔位于長度方向三等分點、寬度方向中點處，如圖2所示。使用精度2%、分辨率0.1%的DB115-30濕度傳感器進行相對濕度測量，取兩孔平均值作為其最終值。

表2 CSM-2.36RFA試樣的最大干密度和最佳含水量Table 2 Maximum dry densities and optimum moisture contents of CSM-2.36RFA specimens

由于試件制備采用靜壓成型，直接埋設濕度傳感器會使其損壞，課題組前期試驗采用預留孔洞放置傳感器并密封進行濕度測量；由于試件早期濕度大于95%，傳感器易測量不準甚至損壞，因此本文不采用埋設濕度傳感器的方法，而是測量時快速插入濕度傳感器并用一側帶有凹槽的特制橡膠塞塞緊孔口，不測量時用橡膠塞塞緊孔口并粘貼膠帶防止其失水。

標準養護7 d后在側面粘貼靈敏度為0.1 με的JM-212振弦應變計用于應變測量，采用石英石作為溫度補償片以減小線膨脹系數誤差。為模擬CSM-2.36RFA一維方向的水分遷移，除正方形小面(水分遷移面)外，其余各面均用塑料薄膜和膠帶密封。將其置于溫度(20±1) ℃，濕度(60±5)%環境下進行相對濕度和干縮應變的測量，前28 d每天測量一次，28～40 d每兩天測量一次，40～120 d每十天測量一次，120～180 d每月測量一次。干縮應變計算公式如式(1)：

εsh=εt+εQ.

(1)

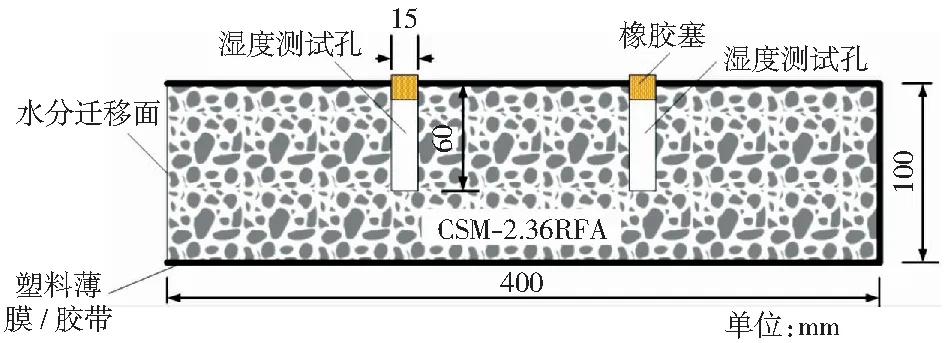
圖2 干燥收縮試樣示意圖Fig.2 Diagram of the test specimen for drying shrinkage

式中：εsh為CSM-2.36RFA的實際總干燥收縮應變(10-6)；εt為CSM-2.36RFA的應變計數值(10-6)；εQ為溫度補償片應變(10-6).

2 結果與討論

2.1 無側限抗壓強度

B3、CEB/FIP、ACI209和GL2000等[6-9]模型均證實了水泥基材料收縮與其抗壓強度有一定的關系，因此本文對CSM-2.36RFA的28 d無側限抗壓強度(UCS)進行了測試，得到圖3所示結果。由圖3可知，當水泥摻量為4%時，CSM-2.36RFA的28 d UCS隨RFA摻量的增加而降低，推測其原因：一方面是強度較低的水泥砂漿同粘附在再生集料上的砂漿形成大的砂漿團塊，容易被外力分離，另一方面是再生集料-水泥砂漿的界面結合強度較低[10]。當水泥摻量為5%和6%時，CSM-2.36RFA的28 d UCS隨RFA摻量的增加先增大后減小，30%摻量時其值最大，這是由于當RFA摻量小幅增加時，其表面未水化的水泥漿與水進一步發生水化反應，加強了與集料的附著力，此外RFA較高的吸水率也起到了一定的內養護作用，促進了水泥的水化；但隨著RFA摻量的進一步增加，其自身強度下降幅度大于水化反應產生的強度，因此強度下降。

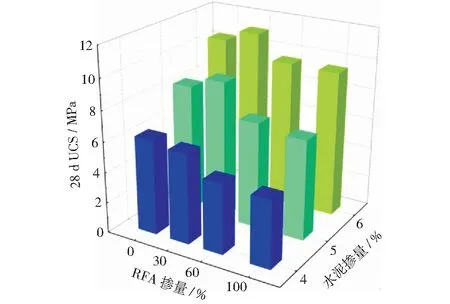
圖3 不同RFA和水泥摻量CSM-2.36RFA的28 d UCSFig.3 28 d UCS of CSM-2.36RFA with different content of RFA and cement

2.2 水穩碎石相對濕度

2.2.1相對濕度變化規律

CSM-2.36RFA的相對濕度變化規律如圖4所示，隨養護齡期的增加，其相對濕度降低，這主要是CSM-2.36RFA內部水分遷移，通過端面散失所導致。且同齡期時，RFA的含量越大，CSM-2.36RFA的相對濕度越大，因為RFA吸水率高，使得CSM-2.36RFA在成型時吸水較多，養護時水分不易散失，導致濕度降低較少。隨養護齡期的增加，CSM-2.36RFA相對濕度降低的速度先快后慢。分析其原因發現，收縮的前30 d內水泥水化過程迅速，水分遷移速率也相對較快；隨養護齡期的增加，水泥水化趨于穩定，反應速率降低，且水化產物使得水穩碎石結構變得致密，水分遷移速率降低。

將t時刻相對濕度與初始相對濕度的差值定義為相對濕度衰減量，如式(2)：

ΔR=H0-Rt.

(2)

式中：ΔR為相對濕度衰減量，%；Rt為t時刻的相對濕度，%；R0為初始相對濕度，%.

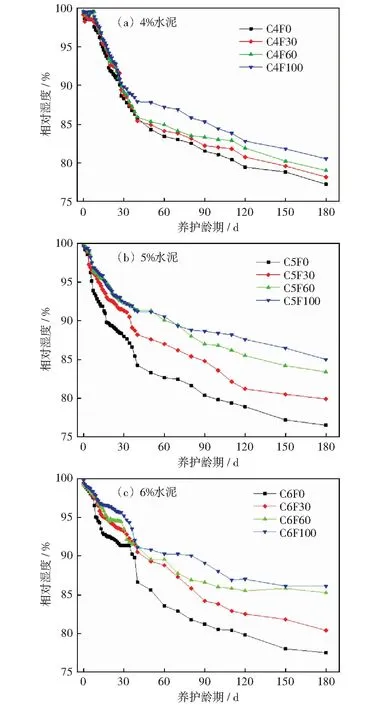
圖4 CSM-2.36RFA試樣相對濕度隨養護齡期的變化Fig.4 Variation in the relative humidity of CSM-2.36RFA specimens with curing period

對不同RFA摻量CSM-2.36RFA的180 d相對濕度衰減量的平均值進行計算可以發現，4%、5%和6%水泥摻量下，其值分別為20.7%、18.5%和17.1%，可知隨水泥摻量的增加，CSM-2.36RFA相對濕度降低的幅度減小。這是因為水泥摻量增加時，水化反應生成的產物增多，使結構更加致密，水分不易散失。

2.2.2相對濕度預測模型

參考文獻[22]，并基于大量試驗數據分析，最終得到不同齡期的CSM-2.36RFA相對濕度R(t，ωRFA)隨RFA摻量呈非線性關系，可表示為：

(3)

式中：Kt是與水泥摻量有關的系數，按式(4)計算；ωRFA為RFA摻量，%；R(t,0)為RFA摻量為0時水穩碎石(即天然集料水穩碎石)的相對濕度，%，按式(5)計算。

Kt=a×(1-e-0.04t) .

(4)

(5)

式中：a、b、c為與水泥摻量相關的系數，列于表3中；t為養護齡期，d.

表3 相對濕度預測模型參數Table 3 Parameters of relative humidity prediction model

由式(4)可知，時間影響系數Kt均大于0，且隨齡期的增加而增大，這說明RFA的摻入對CSM-2.36RFA相對濕度的降低起到一定的緩解作用，這可能是由于RFA對CSM-2.36RFA起到了一定的內養護作用。隨著齡期的增加，Kt的增大速率逐漸降低，原因是RFA的內養護效果逐漸減弱。

圖5顯示了CSM-2.36RFA相對濕度模型和試驗值的對比，計算分析可知R2均大于0.9，表明理論模型與試驗結果吻合度良好，上式可以較為準確地預測CSM-2.36RFA的相對濕度。

圖5 不同水泥摻量CSM-2.36RFA的相對 濕度理論模型與試驗數據Fig.5 Relative humidity of theoretical model and test data of CSM-2.36RFA with different cement content

2.3 水穩碎石干燥收縮

2.3.1干燥收縮變化規律

圖6給出了不同配比CSM-2.36RFA干燥收縮試驗結果，由圖6可知，CSM-2.36RFA的干燥收縮應變隨養護時間的延長而增大。在傳統干燥收縮試驗中，CSM在約30 d后達到最終干縮，然后趨于穩定[10,23]，但本文中CSM-2.36RFA的干燥收縮發展較傳統試驗慢很多。這是因為RFA吸水率較高，成型后不易失水，此外，試樣用塑料薄膜和膠帶包裹，有效防止水分的大量散失。試驗還發現，隨著RFA摻量的增加，CSM-2.36RFA的干縮應變增大，可以發現其與UCS成負相關，這與混凝土性質類似[24]。

圖6 CSM-2.36RFA試樣干燥收縮應變隨養護齡期的變化Fig.6 Variation in the drying shrinkage strain of CSM- 2.36RFA specimens with curing period

對180 d時不同RFA摻量CSM-2.36RFA與天然水穩碎石進行對比可知：4%水泥摻量時，30%、60%和100%RFA摻量CSM-2.36RFA分別增大21.1%、31.9%和71.8%；5%水泥時，分別增大40.9%、42.8%和94.4%；6%水泥時，分別增大46.3%、51.3%和119.5%。由此可知水泥摻量增加時，RFA摻量對CSM-2.36RFA的180 d干縮應變影響變大。

2.3.2干燥收縮預測模型

混凝土干燥收縮預測模型表示其干燥收縮應變與養護齡期之間的關系函數，國內外研究人員得到了較多的預測模型，研究發現其中ACI209模型缺乏尺寸效應，存在大量的散點和不符合邏輯的發展趨勢，CEB/FIP模型低估了收縮發展，B3模型采用實際配合比，有利于收縮預測，其收縮模型優于CEB/FIP模型，GL2000模型在B3模型基礎上更加優化，因此GL2000模型被廣泛應用于混凝土干縮預測[8]。

然而，水穩碎石干燥收縮預測模型的研究屈指可數，且均未考慮RFA摻量的影響。由上節可知CSM-2.36RFA 的干縮主要受時間、水泥摻量和RFA摻量的影響，且為模擬水分在一維方向的遷移，試件五個面均用塑料薄膜和膠帶包裹，其干縮發展與傳統情況相比較慢，因此，本文在混凝土GL2000干縮模型的基礎上，對其時間影響系數進行修正，提出了適用于CSM-2.36RFA的干縮預測模型，公式如式(6)所示，該公式適用于一維方向水分遷移，齡期為180 d內，水泥摻量為4%～6%的CSM-2.36RFA干縮應變預測。

εsh=εshuβ(h)β(t) .

(6)

式中：εshu為干縮應變終值，計算公式如式(7)；β(h)、β(t)分別為濕度影響系數、時間影響系數，計算公式如式(8)-(9).

(7)

β(h)=1-1.18h4.

(8)

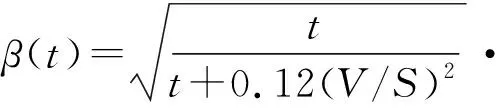
(9)

式中：K為水泥類型參數，P.O 42.5時K取1；fcu為CSM-2.36RFA的28 d UCS，MPa；h為環境濕度，%；V/S為體表比，mm；ωC為水泥摻量，%.

通過上述公式可以發現，時間影響系數隨RFA摻量和水泥摻量的增加而增大，由此可知CSM-2.36RFA的干縮應變與RFA摻量和水泥摻量均呈正相關，可以較為準確地反映RFA和水泥摻量對其影響規律。

圖7對CSM-2.36RFA干縮預測模型和試驗值進行了對比，經計算可知R2均大于0.9，說明預測模型擬合度良好，能夠較為準確地預測180 d內CSM-2.36RFA的干縮應變。

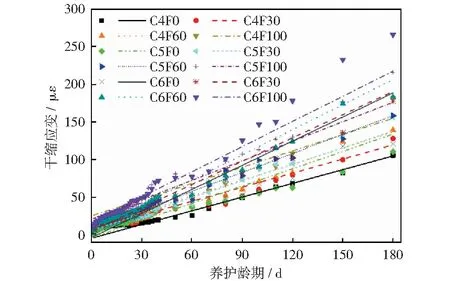
圖7 CSM-2.36RFA干燥收縮應變理論模型與試驗數據Fig.7 Drying shrinkage strain of theoretical model and test data of CSM-2.36RFA

2.4 水穩碎石相對濕度與干燥收縮的關系

水穩碎石內部水分遷移引起濕度降低，導致其內部毛細孔失水產生毛細孔壓力，吸附水蒸發使膠凝體靠近，在毛細管作用、吸附水作用和分子間力的作用下發生干燥收縮[25]。根據上述兩節內容的介紹可知，當RFA摻量增加時，CSM-2.36RFA的相對濕度增大，其水分散失減小，然而其干燥收縮卻增大，這與全部粒徑替代的水穩再生碎石不同[23，26]。可能是因為RFA主要是從路面板廢棄混凝土中破碎研磨所得，其比表面積較大，微裂紋多，對水有較大的親和力，可以顯著減少CSM-2.36RFA中的游離水，且RFA在摻入水穩碎石前含水率為0，其較大的吸水率會從其余碎石和膠凝材料中奪取水分，造成內部毛細孔水分驟失，且在水泥水化過程中RFA中水分不易散失，因此在相同的水分蒸發速率下，RFA顯著增加了毛細管負壓，使CSM-2.36RFA表現出更大的塑性收縮。

為明確CSM-2.36RFA干縮應變與相對濕度之間的關系，將CSM-2.36RFA干縮應變和相對濕度衰減量試驗數據進行分析，如圖8所示，其關系滿足式(10).參數α和β的大小受水泥摻量和RFA摻量的影響，其關系如式(11)、(12)，且擬合程度較好，因此可根據相對濕度的變化預測干燥收縮發展。

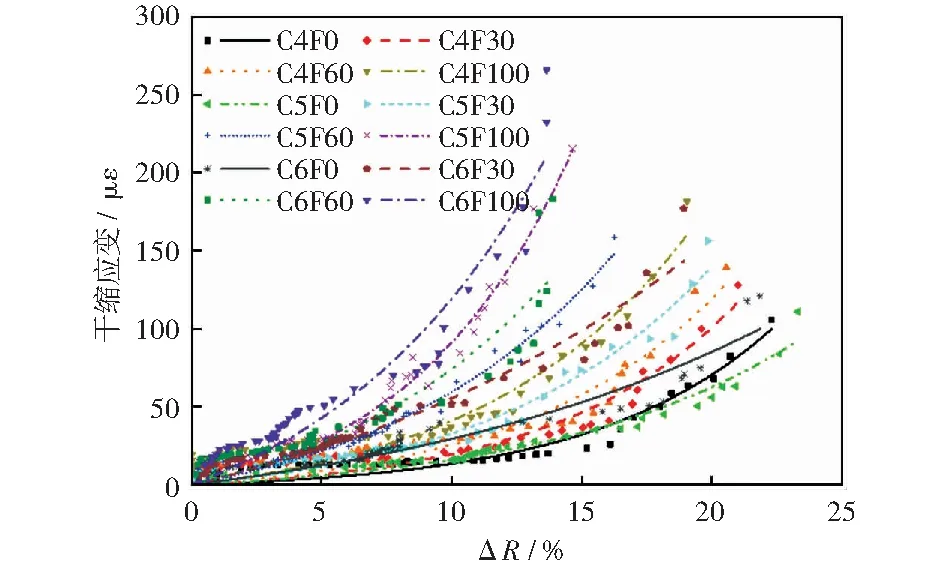
圖8 CSM-2.36RFA干燥收縮應變和相對 濕度衰減量關系擬合曲線Fig.8 Fitting curve of the relationship between drying shrinkage strain and relative humidity decay of CSM-2.36RFA

(10)

(11)

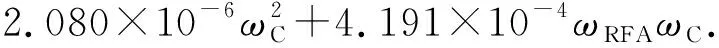
(12)

3 結論

本文設計了不同水泥摻量和0～2.36 mm RFA摻量的12組配合比，對CSM-2.36RFA的相對濕度和干燥收縮進行了測量，建立了其相對濕度和干燥收縮預測模型。可以得到以下結論：

1) CSM-2.36RFA相對濕度與0～2.36 mm RFA摻量、水泥摻量以及養護齡期有關，隨養護齡期的增加，其相對濕度降低；同齡期時，0～2.36 mm RFA的含量越大，其相對濕度越大；隨水泥摻量的增加，相對濕度降低的幅度減小。建立了CSM-2.36RFA相對濕度的數學模型，用于預測其相對濕度。

2) CSM-2.36RFA干燥收縮應變隨養護齡期和0～2.36 mm RFA摻量的增加而增大，且與UCS密切相關；水泥摻量增加時，0～2.36 mm RFA摻量對CSM-2.36RFA的180 d干縮應變影響變大。參考混凝土GL2000模型，考慮CSM-2.36RFA的0～2.36 mm RFA摻量和水泥摻量等因素，得到CSM-2.36RFA的干燥收縮預測模型，與試驗值對比發現其擬合度良好，能較為準確地預測一維水分遷移狀態下，180 d內水泥摻量為4%～6%CSM-2.36RFA的干燥收縮應變。

3) 當0～2.36 mm RFA摻量增加時，CSM-2.36RFA的相對濕度增大，水分散失減小，然而其干燥收縮卻增大，這與全部粒徑替代的水穩再生碎石不同。對試驗數據進行分析得到了CSM-2.36RFA的干燥收縮應變與相對濕度衰減量之間的關系，且擬合度良好，可根據相對濕度的變化預測干燥收縮發展。