寡頭競爭下航線網(wǎng)絡(luò)選擇的動態(tài)博弈模型

景崇毅，盧 燕，吳孟瑤

（中國民航飛行學(xué)院經(jīng)濟與管理學(xué)院/機場管理與工程研究中心，廣漢 618307）

0 引言

國際經(jīng)驗表明，布局合理的航線網(wǎng)絡(luò)能夠極大地提升整個國家的民航運輸效率，對推動民航運輸生產(chǎn)發(fā)展和國家綜合交通運輸系統(tǒng)建設(shè)具有重要的戰(zhàn)略意義。民航十四五規(guī)劃提出要構(gòu)建布局完善、高效率運行的航空運輸網(wǎng)絡(luò)體系。以國際樞紐和區(qū)域樞紐機場為支點，構(gòu)建高聯(lián)通、廣覆蓋、便捷經(jīng)濟的國內(nèi)航線網(wǎng)絡(luò)，不斷提升網(wǎng)絡(luò)整體效應(yīng)。對于航空公司而言，航線網(wǎng)絡(luò)是航空公司生存和發(fā)展的基礎(chǔ)，是提高自身競爭力的有效途徑，它不僅受到宏觀管理政策、區(qū)域發(fā)展環(huán)境、航線網(wǎng)絡(luò)模式的影響，同時也受到市場需求狀況、供給分布以及競爭環(huán)境等諸多因素的影響，是一項非常重要且復(fù)雜的戰(zhàn)略決策。研究航線網(wǎng)絡(luò)決策問題具有重要的現(xiàn)實意義和理論價值。

國外學(xué)者對航線網(wǎng)絡(luò)選擇的課題已有一定的研究成果。Kawasaki考察了一家航空公司在考慮需求方網(wǎng)絡(luò)效應(yīng)和旅客時間價值異質(zhì)性的情形下，如何選擇航線網(wǎng)絡(luò)結(jié)構(gòu)。Alderighi等在博弈論框架下討論了航空公司航線網(wǎng)絡(luò)結(jié)構(gòu)的設(shè)計問題。Barla和Constantatos研究了在一個三航點網(wǎng)絡(luò)中需求不確定性對壟斷航空公司網(wǎng)絡(luò)結(jié)構(gòu)的影響。Oum等通過一個三城市網(wǎng)絡(luò)上的雙寡頭博弈，分析放松管制后航空公司之間的戰(zhàn)略互動對其網(wǎng)絡(luò)選擇的影響。Barla和Constantatos采用古諾靜態(tài)博弈模型研究了需求不確定性和競爭對航空公司網(wǎng)絡(luò)結(jié)構(gòu)選擇的影響。Aguirregabiria和Ho基于動態(tài)博弈模型從需求、成本和戰(zhàn)略角度研究了美國的樞紐輪輻式網(wǎng)絡(luò)。Zhe建立了一個不同于Barla和Constantatos的三階段網(wǎng)絡(luò)競爭模型，分別包括：網(wǎng)絡(luò)結(jié)構(gòu)決策、航班頻率決策、產(chǎn)品定價決策。該模型主要從實證的角度分析航空公司合并的網(wǎng)絡(luò)效應(yīng)，以及網(wǎng)絡(luò)外部性對網(wǎng)絡(luò)結(jié)構(gòu)的影響。Lin研究了兩家樞紐公司通過建立子公司開展網(wǎng)絡(luò)競爭的問題。Silva等基于雙寡頭模型，考慮擁堵外部性、航班頻率、中轉(zhuǎn)成本及樞紐區(qū)位等因素，研究了航空公司的網(wǎng)絡(luò)競爭策略，同時還分析了監(jiān)管者如何通過機場定價引導(dǎo)航空公司構(gòu)建最優(yōu)的網(wǎng)絡(luò)結(jié)構(gòu)。Babi?和Kali?研究了雙寡頭競爭環(huán)境中航空公司如何選擇航線網(wǎng)絡(luò)結(jié)構(gòu)，模型中考慮了產(chǎn)品差異化、航班頻率、運力大小及平均航程等因素。Yang等建立一個雙層規(guī)劃模型，從動態(tài)交互的角度研究了寡頭競爭市場中航空公司如何設(shè)計最優(yōu)航線網(wǎng)絡(luò)的問題，并利用臺灣航空市場數(shù)據(jù)進行驗證。Ciliberto和Zhang利用美國航空業(yè)數(shù)據(jù)檢驗了三個不同的市場進入模型：同時進入博弈、無戰(zhàn)略威懾的進入博弈、有戰(zhàn)略威懾的進入博弈，結(jié)論是現(xiàn)實數(shù)據(jù)最契合有戰(zhàn)略威懾的進入博弈模型。Lordan等研究了不同商業(yè)模式的航空公司的網(wǎng)絡(luò)魯棒性，發(fā)現(xiàn)低成本航空的網(wǎng)絡(luò)魯棒性優(yōu)于全服務(wù)航空。Ren利用靜態(tài)進入博弈模型研究美國西南航空進入某網(wǎng)絡(luò)后對其他航空公司支付函數(shù)和進入概率的影響。

國內(nèi)學(xué)者對航線網(wǎng)絡(luò)選擇問題的研究并不充分，大多數(shù)研究集中在基于優(yōu)化模型的網(wǎng)絡(luò)設(shè)計問題。如柏明國等利用最短路優(yōu)化算法求解樞紐網(wǎng)絡(luò)的設(shè)計問題。鄧亞娟等建立了需求不確定有容量限制的樞紐航線網(wǎng)絡(luò)設(shè)計模型。高榮環(huán)和楊芳研究了競爭環(huán)境下樞紐航線網(wǎng)絡(luò)的優(yōu)化設(shè)計方案。樂美龍等基于機場容量包絡(luò)曲線構(gòu)建了隨機需求下多分配、非嚴格的兩階段混合整數(shù)隨機規(guī)劃網(wǎng)絡(luò)模型。李實萍在多個外部選擇、多個市場以及雙寡頭競爭的環(huán)境下，通過構(gòu)建航線網(wǎng)絡(luò)結(jié)構(gòu)選擇的決策模型，研究網(wǎng)絡(luò)結(jié)構(gòu)的不同組合對航空公司競爭績效的影響。汪瑜等針對市場補貼定價決策對航空公司樞紐航線的網(wǎng)絡(luò)設(shè)計影響，基于雙層規(guī)劃思想，分別構(gòu)建航空公司樞紐航線網(wǎng)絡(luò)設(shè)計的上層規(guī)劃模型和各民用運輸機場空運市場補貼定價決策的下層規(guī)劃模型。

通過以上文獻梳理，我們發(fā)現(xiàn)目前關(guān)于航線網(wǎng)絡(luò)選擇的研究還存在兩方面的不足：第一，理論假設(shè)與決策現(xiàn)實不符。現(xiàn)有研究一般基于靜態(tài)博弈模型，即假定競爭者同時決策，或者即使沒有同時決策，但后來者無法觀察到在位者的決策結(jié)果，這與現(xiàn)實并不相符。現(xiàn)實中一般是某家航空公司首先進入某個市場，后進入者可以觀察到在位者的網(wǎng)絡(luò)及運力配置狀況。從博弈的角度看，在位者也必然要考慮到后進入者的存在性及其可能采取的策略。為了更加貼合這種決策現(xiàn)實，本文采用Stackelberg動態(tài)博弈模型進行分析。第二，對不確定性的設(shè)定存在局限性。為了貼合這種決策現(xiàn)實，本文不僅考慮了單一市場本身需求的不確定性，還考慮了不同市場之間的相關(guān)性所導(dǎo)致的不確定性。

1 構(gòu)建三階段博弈模型

1.1 問題表述和參數(shù)說明

在圖1所示的包含三個城市的航線網(wǎng)絡(luò)中，已有一家在位航空公司，現(xiàn)另有一家航空公司將要進入該網(wǎng)絡(luò)與其進行競爭。該城市網(wǎng)絡(luò)中存在一個樞紐城市和兩個非樞紐城市和。、和為航段。當通過樞紐網(wǎng)絡(luò)飛行時，只需通過一個航段來完成一次旅行的旅客被稱為本地市場，而需通過兩個航段（和）來完成一次旅行的旅客被稱為中轉(zhuǎn)市場。對點對點網(wǎng)絡(luò)而言，中轉(zhuǎn)市場指的是原先只能通過樞紐網(wǎng)絡(luò)進行中轉(zhuǎn)的旅客。在本文中，將采用樞紐網(wǎng)絡(luò)的航空公司稱為“樞紐航空公司”，采用點對點網(wǎng)絡(luò)的航空公司稱為“非樞紐航空公司”。模型相關(guān)參數(shù)如表1所示。

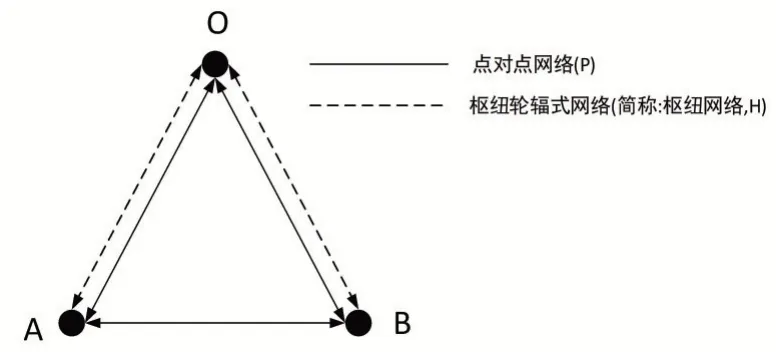
圖1 雙寡頭航空公司在三航點網(wǎng)絡(luò)中的競爭示意圖

表1 模型相關(guān)參數(shù)及含義匯總

續(xù)表1

我們將航空公司戰(zhàn)略決策劃分為三個階段，在每一階段，航空公司都進行一場完全信息下非合作的動態(tài)博弈。后進入的航空公司能夠觀察到在位航空公司選擇的策略，故而后進入航空公司能夠利用這些信息做出更理性的決策。三階段決策內(nèi)容分別如下：

第一階段：需求未知時，航空公司選擇航線網(wǎng)絡(luò)結(jié)構(gòu)：樞紐網(wǎng)絡(luò)()或點對點網(wǎng)絡(luò)()。

第二階段：需求仍未知下，航空公司進行運力決策。運力投入是一項長期決策，取決于航空公司擁有的飛機數(shù)量、機場可用登機口和起降時刻的數(shù)量。如果在第一階段選擇了樞紐網(wǎng)絡(luò)，那么航空公司將決定同時為本地和中轉(zhuǎn)市場提供的運力；如果選擇了點對點網(wǎng)絡(luò)，航空公司將分別確定為本地和中轉(zhuǎn)市場提供的運力。“運力”一詞是指每家航空公司每條航線每周或每月能提供的最大座位數(shù)量。我們假定運力成本取決于網(wǎng)絡(luò)結(jié)構(gòu)，由于樞紐航空公司需要更多的樞紐資源投入和更復(fù)雜的調(diào)度管理，因此c＞c。

第三階段：需求已知后，基于前兩個階段已經(jīng)確定的網(wǎng)絡(luò)結(jié)構(gòu)和運力，航空公司參與Stackelberg數(shù)量博弈。本文中的“數(shù)量”是指受運力限制的航空公司每周或每月提供的實際座位數(shù)量。在需求明確后的第三階段，樞紐航空公司仍然可以在本地市場和中轉(zhuǎn)市場之間分配運力，而非樞紐航空公司卻沒有這樣的靈活性。第三階段的博弈是兩個市場的動態(tài)競爭，航空公司爭奪中轉(zhuǎn)旅客和本地旅客。

通過逆推歸納法來求解博弈均衡。在需求不確定性解決后，航空公司在第三階段的問題是已知在位航空公司的運力和網(wǎng)絡(luò)結(jié)構(gòu)的情況下，選擇數(shù)量q(=1,2)來最大化π。由于航空公司的運營成本主要與總座位數(shù)有關(guān)，旅客的邊際成本很小，可以忽略不計，因此將其視為零。在第二階段運力博弈中，航空公司在給定網(wǎng)絡(luò)結(jié)構(gòu)的情況下，確定均衡運力。最后在第一階段博弈中，航空公司考慮到在位航空公司的網(wǎng)絡(luò)結(jié)構(gòu)決策，根據(jù)預(yù)期利潤∏來確定自身的網(wǎng)絡(luò)結(jié)構(gòu)。此外，為了確保航空公司在市場上的非負利潤，令c≤u/2和c≤u/2。

1.2 模型創(chuàng)建

已知在位航空公司（公司1）的網(wǎng)絡(luò)結(jié)構(gòu)，新進入航空公司（公司2）有兩種網(wǎng)絡(luò)結(jié)構(gòu)選擇（或）。新進入航空公司的最佳響應(yīng)網(wǎng)絡(luò)結(jié)構(gòu)可以通過圖2所示的博弈樹來確定。

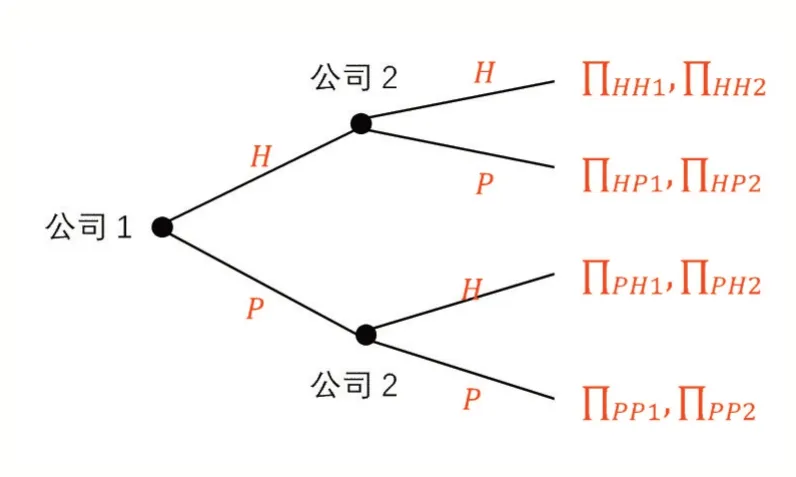
圖2 航空公司網(wǎng)絡(luò)結(jié)構(gòu)的序貫博弈示意圖

如果航空公司采用的是樞紐網(wǎng)絡(luò)，那么它在第二和第三階段的問題可以分別表示如下：

如果航空公司采用的是點對點網(wǎng)絡(luò)，那么它在第二和第三階段的問題可以分別表示如下：

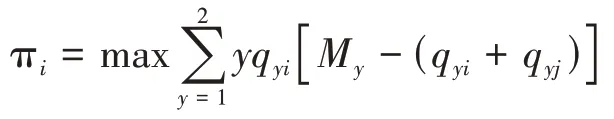
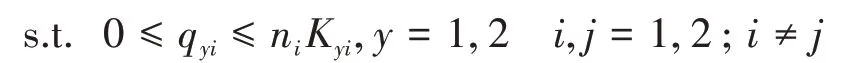
因為樞紐航空公司在第三階段決策中仍然可以在本地市場和中轉(zhuǎn)市場之間分配運力，因此，當雙寡頭博弈中有樞紐航空公司參與時，仍需將運力博弈和數(shù)量博弈單獨分析，即該博弈仍是三階段博弈。只有當兩家航空公司都采用點對點網(wǎng)絡(luò)時，三階段博弈才退化為兩階段博弈。

1.3 假設(shè)條件

（1）為了簡化分析，假設(shè)本地市場是對稱的。市場、具有共同的需求函數(shù)，并且三個市場、和都是雙向?qū)ΨQ的，即從到的流量與從到的流量具有相同的特性。

（2）樞紐航空公司總是服務(wù)于中轉(zhuǎn)市場（文獻［6］中所述）。

（3）每一家航空公司都耗盡了它的運力（文獻［5］和［11］中所述）。對于樞紐航空公司來說，+=n K；對于非樞紐航空公司來說，q=n K。強加假設(shè)（2）和（3）的目的是為了使市場出清，模型的分析處理更清晰明了，但并不會影響基本結(jié)論。

2 航線網(wǎng)絡(luò)決策的博弈分析

我們通過比較航空公司在運力博弈中的預(yù)期利潤來對網(wǎng)絡(luò)結(jié)構(gòu)博弈均衡進行分析。

2.1 博弈分析

首先根據(jù)第三階段的Stackelberg博弈確定座位數(shù)量，在此基礎(chǔ)上計算均衡運力，最后比較不同網(wǎng)絡(luò)結(jié)構(gòu)下的利潤函數(shù)，以確定采用何種形式的網(wǎng)絡(luò)結(jié)構(gòu)。

表2和表3分別給出了寡頭航空公司網(wǎng)絡(luò)博弈的均衡運力及均衡利潤，其中，第一、二項表達式分別表示在位航空公司和新進入航空公司的均衡運力及均衡利潤。

表2 寡頭壟斷情形下航空公司動態(tài)博弈的均衡運力

表3 寡頭壟斷情形下航空公司動態(tài)博弈的均衡利潤

證明：在假設(shè)條件下，以在位航空公司采用點對點網(wǎng)絡(luò)，新進入航空公司采用樞紐網(wǎng)絡(luò)為例進行證明，通過逆推歸納法求解均衡運力和利潤。其余三種情況的證明與其類似。

（1）新進入航空公司(=2)在數(shù)量博弈中的利潤如下：

通過分別求解關(guān)于和的一階條件，解得：

該航空公司在運力博弈中的利潤如下：

將和代入后，求解關(guān)于的一階條件，解得：

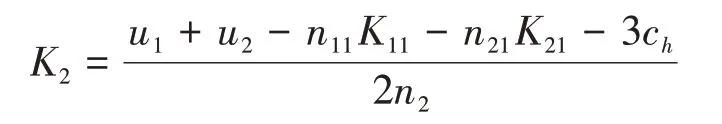
因為后進入的航空公司在選擇數(shù)量之前會觀測到在位航空公司的數(shù)量，因此會根據(jù)在位航空公司投入的數(shù)量來選擇自己的數(shù)量。將代回和后，會得到新進入航空公司關(guān)于在位航空公司數(shù)量的反應(yīng)函數(shù)，即：

（2）在位航空公司(=1)在數(shù)量博弈中的利潤如下：

分別求解關(guān)于和的一階條件，解得：

之后均衡運力及利潤便可求出。

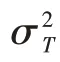
2.2 均衡網(wǎng)絡(luò)分析

考慮到在位航空公司的網(wǎng)絡(luò)結(jié)構(gòu)，我們現(xiàn)對新進入航空公司最佳的響應(yīng)網(wǎng)絡(luò)進行分析。通過表3推導(dǎo)出以下命題。

命題1：

（i）如果在位航空公司采用樞紐網(wǎng)絡(luò)，則滿足以下條件時，新進入者的最佳響應(yīng)網(wǎng)絡(luò)是樞紐網(wǎng)絡(luò)：

（ii）如果在位航空公司采用點對點網(wǎng)絡(luò)，則滿足以下條件時，新進入者的最佳響應(yīng)網(wǎng)絡(luò)是樞紐網(wǎng)絡(luò)：

證明：（i）在位者采用樞紐網(wǎng)絡(luò)時，令Δ∏=∏-∏＞0，

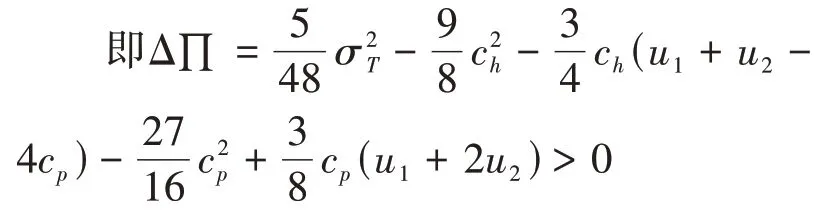
（ii）的證明與（i）類似。

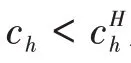
3 結(jié)語

本文運用動態(tài)博弈理論，研究了完全信息下雙寡頭航空公司的航線網(wǎng)絡(luò)選擇問題。為此，我們構(gòu)建了一個三階段動態(tài)博弈模型。在第一階段，航空公司首先確定自己的網(wǎng)絡(luò)結(jié)構(gòu)；第二階段，在需求未知下，航空公司確定投入的運力；第三階段，需求已知后，利用Stackelberg模型，分析雙寡頭航空公司的數(shù)量博弈。通過逆推歸納法求解整個博弈的均衡解。

本文所使用的動態(tài)博弈模型考慮了市場不確定因素，通過假定市場上的需求符合線性逆需求函數(shù)p=M-(q+q)來實現(xiàn)，通過該需求函數(shù)，可以設(shè)定市場不確定性，不僅考慮了單一市場本身需求的不確定性外，還考慮了不同市場之間的相關(guān)性所導(dǎo)致的不確定性。而一般的動態(tài)博弈只是假定逆需求函數(shù)為p=-(q+q)，其中一般為常數(shù)，因此如果選擇一般的動態(tài)博弈模型進行分析，則無法研究市場不確定性對航空公司網(wǎng)絡(luò)結(jié)構(gòu)選擇的影響，以及市場規(guī)模對航空公司運力配置決策產(chǎn)生的影響。

基于假定條件，我們得到了雙寡頭航空公司博弈的均衡運力、均衡利潤。研究發(fā)現(xiàn)，非樞紐航空公司在某市場上的均衡運力僅取決于該市場需求均值，而樞紐航空公司的均衡運力會受到兩個市場需求均值的影響。市場不確定性為樞紐網(wǎng)絡(luò)提供了巨大的靈活性價值，在競爭環(huán)境下，這種靈活性價值仍然存在。新進入者的最佳網(wǎng)絡(luò)決策實質(zhì)上是權(quán)衡靈活性價值和成本優(yōu)勢。當單位運力成本較低時，新進入者更傾向于獲取靈活性價值，此時采用樞紐網(wǎng)絡(luò)。