基于ARIMA與SVR滾動殘差模型組合的股票預測

陳登建　杜飛霞　夏換

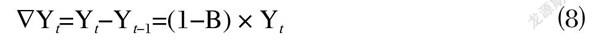
摘? 要： 為提高金融市場股票的預測精確度，提出自回歸差分移動平均與支持向量機滾動殘差模型組合的預測股票方法。以貴州茅臺的股票數據為研究對象，借助ARIMA模型實現對股票數據的線性趨勢預測，通過滾動殘差的SVR回歸模型對ARIMA模型的預測殘差進行數據修正，得到ARIMA_SVR滾動殘差模型的預測值。實驗結果表明，相較于傳統ARIMA模型，ARIMA與滾動殘差SVR組合模型的性能和預測精度都得到大幅提升，具有一定的學術價值和應用意義。

關鍵詞： 金融; ARIMA模型; SVR滾動殘差模型; 股票預測

中圖分類號：TP183? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2022）05-76-05

Stock forecasting based on the combination of ARIMA and SVR rolling residual model

Chen Dengjian ?Du Feixia Xia Huan

Abstract： In order to improve the accuracy of stock prediction， a prediction method based on the combination of autoregressive differential moving average and support vector machine rolling residual model is proposed. Taking the stock data of Guizhou Maotai as the research object， the ARIMA model is used to realize the linear trend prediction of the stock data. The predicted residuals of the ARIMA model are corrected by the SVR regression model of the rolling residuals， and the predicted values of the ARIMA_SVR rolling residuals model are obtained. The experimental results show that compared with the traditional ARIMA model， the performance and prediction accuracy of ARIMA and rolling residual SVR combined model have been greatly improved， which has certain academic value and application significance.

Key words： finance; ARIMA model; SVR rolling residual model; stock forecast

引言

我國股票二級市場的漲跌受到多種因素的影響，由于其不平穩、非線性等特點，導致為實現對股票數據的精確預測變得尤為困難。挖掘股票的波動規律，預測股票漲跌情況，有利于促進中國金融市場的穩定。

我國早期對股票走勢預測主要包括對于基本面的分析和技術面的分析。基本面的分析是通過分析公司的運營情況和行業的發展態勢，預測該公司股票的未來走勢。技術的分析主要是分析金融市場各個因素，例如股票的成交量、成交價格等因素。

隨著研究的進展，學者們以時間為維度構建出ARIMA模型，根據股票歷史價格走勢對股票進行短期預測[1-6]。計算機技術的發展，各種智能算法也越發的成熟，眾多學者將機器學習的智能算法應用在股票數據的研究分析。如丁文絹通過構建ARIMA與LSTM神經網絡模型，實現股票走勢的預測，LSTM神經網絡模型相較于ARIMA模型預測誤差更小[7];鄒菊紅借助BP反向傳播的神經網絡模型實現對于股票價格的預測[8];齊甜方借助Seq2Seq和情感分析實現對于股票波動趨勢的預測[9]。

本文選貴州茅臺的股票價格數據[1]作為實驗的研究對象，提出一種改進的差分自回歸移動平均模型（ARIMA）與滾動殘差的支持向量機回歸模型（SVR）的組合，利用殘差數據優化模型的參數，實現對貴州茅臺高準確率的預測。

1 研究方法

1.1 ARIMA模型

時間序列是以時間作為自變量，隨著時間變化并且互相關聯的數據。ARIMA模型是經典的時間序列模型[10]，該模型含義表達為將非平穩的序列轉化為平穩的序列，用當前變量的滯后項，以及隨機的誤差值來解釋當前變量，模型的輸入為時間序列的單變量，該模型的表達式可以用式⑴來表示。

⑴

其中?i的i取值從1到p，θi的i取值從1到q。其分別代表ARIMA模型參的參數p和q，p是自回歸模型的系數，q是移動平均模型的系數。

ARIMA（p，d，q）模型要求當前的時間序列是一個平穩的時間序列，平穩的序列的時間平移長度，可以決定當前函數的自相關與協方差，如下所示：

⑵

γ （t，s）表示為序列{Xt}的自相關協方差函數，μ為常數。時間序列進行差分處理后，可以將非平穩的時間序列轉為平穩的時間序列，再將AR自回歸模型與MA移動平均模型組合成ARIMA模型，該模型完整建模函數為：

⑶

⑷

⑸

函數⑶中?表示差分算法，式⑷代表平滑系數多項式，式⑸代表自回歸系數多項式。

本文的ARIMA建模步驟[11]

⑴ 觀察數據的平穩性，將非平穩的時間序列利用差分處理轉為平穩的時間序列，確定d參數。

⑵ 根據ACF確定自回歸模型中參數p，根據PACF確定模型中的參數q。

⑶ 利用歷史數據對模型進行訓練，預測未來數據。

1.2 SVR模型

支持向量機模型，可以用于樣本數據的分類與預測，用于對于連續值的預測稱為支持向量機的回歸SVR[12]該模型是基于統計學結構風險最小理論作為理論支撐{Yi}（i = 1， 2，…，M），輸入N維的樣本xi∈Rn進行訓練，將樣本xi低維度的特征，通過不同函數算法，映射為高維度的空間，輸出yi∈R預測值。支持向量的線性函數完成數據的預測任務，SVR回歸預測函數的表示為：

⑹

式⑹中Φ（x）完成輸入數據映射為高維數據，通過梯度下降法，迭代訓練，收斂參數w和常數b的值，得到w，b誤差最小值，如下所示：

⑺

式⑺中C表示正則化系數，相較于普通的回歸模型，SVR模型可以調整正則項系數，解決模型的過擬合和欠擬合問題，式中[Lε]為不敏感系數。支持向量機模型中的核函數k（xi，xj）是借助拉格朗日函數和沃爾夫對偶理論將問題轉化為二次規劃問題找最優，常用的核函數有線性核函數Linear kernel，多項式核函數Polynomial kernel，以及徑向基核函數RBF等。

本文的SVR模型的建模步驟

⑴ 將ARIMA預測獲得的殘差，通過不同次的實驗，獲取適宜的循環滾動次數。

⑵ 對數據進行切分，獲得得到訓練集的train_x與train_y，選擇核函數，對SVR模型進行訓練。

⑶ 模型檢驗評估。

1.3 ARIMA_SVR滾動殘差組合模型

本文選取貴州茅臺的股票數據，本文的ARIMA_SVR滾動殘差模型組合實現對未來數據的預測的步驟。

⑴ 借助ARIMA對于該數據線性部分數據處理，獲得股票的漲幅趨勢，以及預測值和殘差。

⑵ 借助SVR解決函數的非線性的部分的數據的擬合，利用SVR模型實現殘差值進行滾動訓練，預測。

⑶ ARIMA模型和SVR模型預測結果疊加，得到最終的預測數據。

2 實例分析

2.1 ARIMA建模

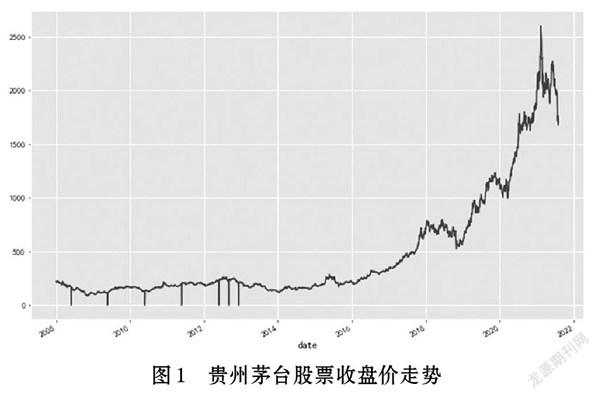
本文選貴州茅臺2008年1月至2021年8月的股票數據作為實驗數據，如圖1所示。

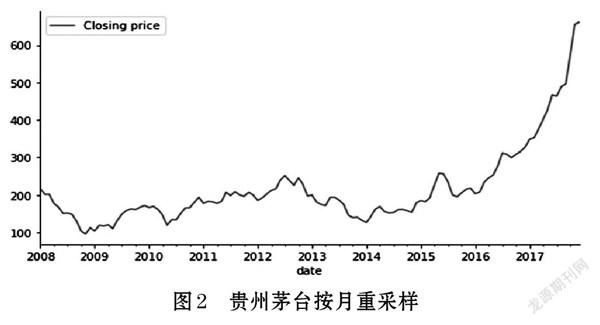
ARIMA建模前，首先需要將采集到的貴州茅臺的股票數據進行預處理，再對股票數據進行重新采樣。因為六日股市不開放，所以數據中存在斷點。通過重新采樣，保證數據之間的連續性，提高到數據預測的精確度[13]。對采集到的貴州茅臺2008-2021年的股票收盤價數據按月進行重采樣，對每個月的數據的總和取得均值，結果如圖2所示。可知貴州茅臺自2008-2014年間波動起伏大，并未有大幅度的上漲，但是自2016年后股票整體的走勢的呈現指數式的上漲的。

股票數據并不平穩，不符合ARIMA對數據的要求，需對數據進行差分處理，轉化為為平穩的時間序列才可預測，差分的公式如下：

⑻

⑼

其中?和?s分別為一階差分算子和周期差分算子;Yt和Yt-1分別表示為當前的實際值與上一個時間的值;B為時間序列的滯后值;s是時間序列的周期。如果經過一階差分處理后，數據還處于不平穩，可以在一階的基礎上，再次進行一次差分處理，直到序列平穩。

貴州茅臺數據差分處理結果如圖3所示，藍色實線Closeing price表示收盤價價格曲線，黃色實線diff_1表示經過對收盤價經過一階差分處理后的波動情況，綠色實線diff_2表示對在一階差分基礎上的再次差分處理。原數據Closeing price數據不平穩，經過一次差分后的數據就已逐步達到平穩。

自回歸AR，可以表示為當前值與序列歷史值之間的相關關系。存在相關性才能用當前變量的歷史數據[14]實現對自身的預測，可以用自相關圖ACF進行初步觀測。模型中移動平均模型MA，利用移動平均來消除在預測當中的隨機波動，可以用偏自相關函數來確定q的值，該函數用來描述中間項的隨機變量對模型的影響，可以用PACF實現對q值的確定。自相關分析和偏自相關分析結果如圖4所示。

本文ARIMA模型根據赤池信息準則（Akaike Information Criterion，AIC）準則作為模型選擇的參考，AIC是日本統計學家Akaike提出，用以擬合精度與參數個數的加權函數，L表示模型參數個數，k表示模型極大似然函數，函數表達式如下：

⑽

最終選擇ARIMA（1，1，1），將數據集進行切分，2008年～2017年劃分為ARIMA訓練數據，對模型進行訓練。將2014～2018為ARIMA預測數據，如圖5所示。

藍色的實線是實際的數據，橙色的直線是預測結果，ARIMA模型已經可以大致的預測出貴州茅臺股票的增長的趨勢，但是實際值與預測值之間的誤差還是較大。

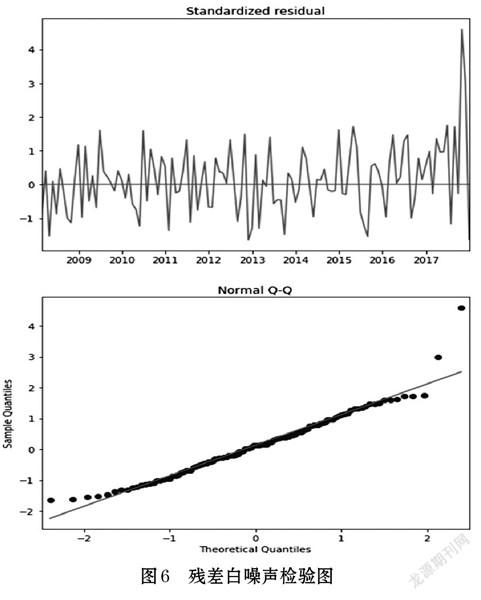
ARIMA殘差的檢驗，主要對殘差數據的自相關性與正態性進行檢驗。ARIMA殘差應當符合正態分布的性質，若殘差數據都集中于0值的附近，那么殘差數據就服從正態分布，即這樣的殘差屬于白噪聲數據。ARIMA模型的殘差檢驗主要用于判別模型是否已經完全捕捉到數據中的信息，性能良好的ARIMA模型的殘差之間不具有相關性，若殘差之間具有相關性，說明數據中還有未挖掘的信息，模型需要進一步優化。性能良好的ARIMA模型的殘差的均值為0，若不為0說明模型中具有偏差。對數據進行白噪聲檢驗，檢驗數據的隨機性，最終的檢測結果如圖6所示。

殘差Normal QQ圖是線性分布則說明模型ARIMA（1，1，1）通過殘差白噪聲檢驗，由Standardized residual圖可知殘差數據符合正態分布，則ARIMA（1，1，1）模型的通過殘差檢驗，且模型性能良好。

2.2 SVR滾動殘差模型修正

計算得到殘差的值，經過多次實驗，最終選定循環滾動4個殘差值，將這4個殘差作為訓練集的特征對SVR模型進行訓練，改模型的訓練還涉及核函數的選定，本文選擇取徑向基核函數作為模型的核函數，因為其不受樣本參數大小的影響的優點，再多次反復實驗發現，對本次貴州茅臺的股票數據集有良好的表現，該核函數如下：

⑾

選定滾動數據集，對模型進行訓練，預測2019年-2021年的股票數據的，結果如圖7所示。

從圖7可以發現，相較于ARIMA模型的單模型，利用SVR模型循環滾動殘差值來修正原模型，已經有了良好的預測效果，模型性能與精度都得到提升。

2.3 預測效果對比分析

分別用ARIMA、SVR和ARIMA-SVR模型對數據對相同的時間區間的真實數據進行預測，通過比較各個模型之間的預測誤差進行對比分析。為評價回歸模型的性能，本文主要采用平均絕對誤差（mean absolute error，MAE）和中位絕對值誤差（mean percentage error，MPE）選用這兩個個指標分別對ARIMA（1，1，1）和ARIMA_SVR模型的預測性能進行評估，這兩個指標的計算如下所示：

⑿

⒀

式⑿中yi的表示數據中的真實值，而[yi]表示模型的預測值，式⒀中MAD代表的是數據點Xi到中位數X的絕對值偏差。這兩個指標的值越小說明，模型的預測的準確性越高，模型的預測性能越好。

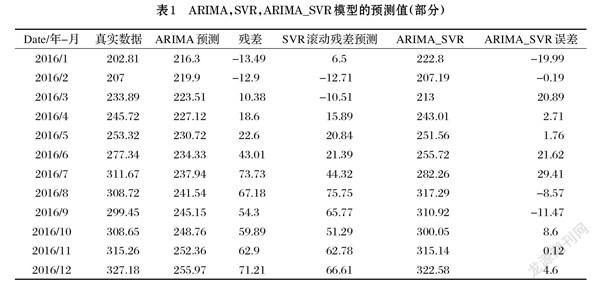
ARIMA，SVR，ARIMA_SVR三個模型的具體的預測值，如表1所示。可見ARIMA_SVR模型的預測誤差相較于單個的ARIMA（1，1，1）模型的預測值誤差，得到了改善。在ARIMA的預測基礎上可以實現預測貴州茅臺股票的大體的趨勢，實現了對于股票數據的線性預測。基于SVR的滾動殘差模型可以對ARIMA（1，1，1）預測的偏差進行修正。

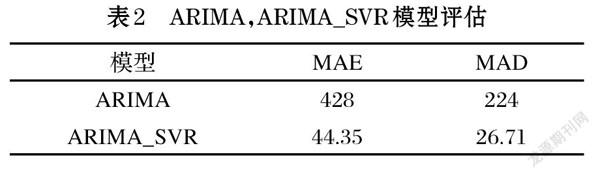
對于ARIMA與ARIMA_SVR模型的預測性能的評估，如表2所示。可以發現相較于單個模型的ARIMA的MAE已經從428降到44.35，MAD從224降到26.71。組合模型有更加良好的預測性能。

3 結束語

近年來，股票受到了越來越多人的追捧。而貴州股票自上市以來股票價格漲幅一直都處于良好趨勢，已然成為股民心中的大股票。針對傳統的股票預測方法預測精度低的問題，本文提出的基于ARIMA時間序列結合測SVR滾動殘差的股票價格的預測模型，以貴州茅臺的股票數據作為研究對象進行實證研究。研究結果表明本文方法是可行、有效的，可以為相關的投資者或者公司進行決策時提供參考策略，避免盲目的投資。

本文的研究不足之處在于，僅以時間的維度作為自變量出發，僅反映在時間序列下數據之間的相關性與規律，這樣可以實現對于股票數據的短期價格的預測。而股票的漲跌受到多種因素的影響，因此，本模型并不能實現對于股票數據的長期的預測。

參考文獻（References）：

[1] 袁仁國.危機時代，激發創新與改革的力量[N].貴陽日報，

2013-12-18（003）

[2] Rao T S，Gabr M M.An introduction to bispectral analysis

and bilinear time series models[M].New York：Springer，2012

[3] Zheng T，Farrish J，KitterlinM.Performance trends of hotels

and casino hotels through the recession：an ARIMAwith intervention analysis of stock indices[J].Journal of Hospitality Marketing & Management，2016，25（1）：49-68

[4] Rangel-Gonzalez J A，Frausto-Solis J，González-Barbosa

JJ，et al.Comparative study of ARIMA methods for forecastingtime series of the mexican stock exchange[J].Studies in Computational Intelligence，2018，749：475-485

[5] 宋剛，張云峰，包芳勛，等.基于粒子群優化LSTM的股票預測

模型[J].北京航空航天大學學報，2019，45（12）：2533-2542

[6] 李超.機器學習模型在股票價格時間序列分析中的應用與

比較[J].電子世界，2021，615（9）：66-70

[7] 丁文絹.基于股票預測的ARIMA模型、LSTM模型比較[J].

工業控制計算機，2021，34（7）：109-112，116

[8] 鄒菊紅.基于BP神經網絡的改進粒子群優化股票預測[J].

山東工業技術，2021，297（1）：34-38

[9] 齊甜方，蔣洪迅.基于Seq2Seq文本摘要和情感挖掘的股票

波動趨勢預測[J].管理評論，2021，33（5）：257-269

[10] 陳維榮，關佩，鄒月嫻.基于SVM的交通事件檢測技術[J].

西南交通大學學報，2011，46（1）：63-67

[11] 李奮華，趙潤林.一種基于時間序列分析的股票走勢預測模

型[J].現代計算機（專業版），2016（20）：14-17

[12] 劉家學，白明皓，郝磊.基于ARIMA-SVR組合方法的航班

滑出時間預測[J].中國科技論文，2021，16（6）：661-667

[13] 楊翠娟.基于機器學習方法的金融股票預測研究[D].湖南

大學，2020

[14] 趙杜羽.基于ARIMA模型的深證成指收盤價的分析和

預測[J].老字號品牌營銷，2021（8）：96-98

收稿日期：2021-10-19

*基金項目：貴州省科技計劃項目（No.黔科合基礎[2019]1041，No.黔科合基礎[2019]1403，No.黔科合基礎[2020]1Y279，No.黔科合基礎[2020]1Y420）; 貴州省教育廳青年科技人才成長項目（No.黔教合KY字[2021]135）

作者簡介：陳登建（1997-），男，福建福州人，碩士研究生，主要研究方向：機器學習，自然語言處理。

通訊作者：夏換（1982-），男，湖南永州人，博士，教授，主要研究方向：計算機仿真，大數據分析。