金屬結構臨時作業棚抗沖擊能力分析

張宇

0 引言

工作人員為了深入分析金屬結構臨時作業棚抗沖擊能力，通過建立木材彈性本構方程以及損傷演化模型，得到木材本構關系模型。并基于ABAQUS 軟件的通用分析模塊與顯示分析模塊，創建材料子程序并進行驗證，在獲得臨時作業棚主要材料性能參數之后，建立臨時作業棚有限元結構模型，模擬高空墜物對臨時作業棚各個部位所造成的沖擊，為提升金屬結構臨時作業棚抗沖擊能力提供數據基礎。

1 建立木材本構模型

從類型上看，木材屬于各向異性材質，當木材受到拉力、剪力時會出現脆性破壞現象，當木材受到壓力則會發生延性破壞。當木材受到沖擊力之后，其各個方向上的拉力屈服強度、壓力屈服強度會存在很大差異。因此，設計人員根據金屬結構臨時作業棚頂部木材的特點，創建木材本構模型（如圖1所示）。

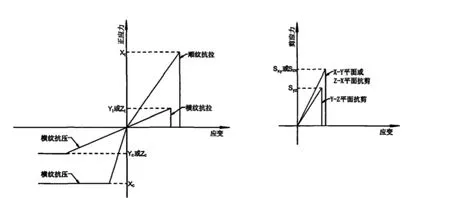
圖1 木材本構模型

通過分析圖1 可以看出，X與X為沿著木材紋理方向的抗壓、拉屈服強度，Z、Z則為木材橫紋切向抗壓、拉屈服強度，Y、Y為木材橫紋徑向抗壓、拉屈服輕度，S、S以及S分別為木材三個平面的抗剪強度。

1.1 木材應力應變關系式

為了方便計算，設計人員將各向異性轉變為正交各向異性，通過轉化可以確定木材的應力－應變關系：

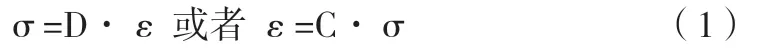
公式（1）中，變量σ 代表應力矩陣，常量C 與D 分別代表木材的柔度矩陣以及剛度矩陣，變量ε 代表木材的應變矩陣。將公式σ=D·ε轉化為矩陣，可以更好地觀察應力應變關系變化。

1.2 構建損傷演化模型

構建損傷演化模型的主要目的是如果材料出現的損傷，可以根據該模型分析材料的彈性模量以及強度等關鍵指標的動態響應情況。該模型以CDM 作為理論基礎，當材料受損之后其柔度矩陣與剛度矩陣呈非線性變化特點。

由于木材屬于各向異性材質，需要使用各向異性屈服準則，才能夠對木材受損情況進行預判。經過眾多科研人員的研究，終于在Sun 與Yamdad 的帶領下，提出Yamada-Sun 屈服準則。該準則認為木材各個軸上的強度相互獨立，某一條軸對應兩個剪應力以及一個正應力，通過計算正應力與剪應力數據，就能確定木材的屈服強度。

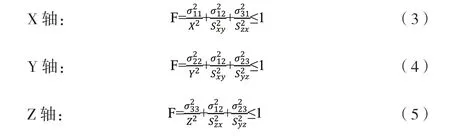
公式（3）（4）（5）中，F 為木材的屈服系數，X、Y、Z則分別代表木材在三個方向上的抗壓強度，依據不同的應力狀態（σ、σ、σ），選擇對應的抗壓強度或者抗拉強度。根據該標準判定木材在受到沖擊之后，各個軸是否屈服。x、y、z 代表木材在抗沖擊實驗中的三個方向，分別為順紋縱向（L），橫紋切向（T）以及橫紋徑向（R）。

2 ABAQUS 程序設計

ABAQUS 系統主要由顯示分析模塊以及通用分析模塊兩個部分組成，前者在準靜態分析中較為常用，后者在靜力分析中較為常見。在運用兩組模塊進行力學分析時，需要在確保慣性力較小的狀態下，用最短的時間進行沖擊模擬，例如沖切以及碰撞等。本次設計中，考慮到高空墜物對于木方的沖擊以準靜態分析為主，因此選擇使用顯示分析模塊模擬高空墜物的沖擊數據。

ABAQUS 系統為用戶提供了大量的材料本構模型以及單元庫，能夠模擬大多數材料受到沖擊之后的形變數據。但是該系統的局限性在于無法直接調用材料本構模型進行實驗，需要借助二次開發平臺，依據實際情況對材料本構模型進行自定義設計。本次實驗中，工作人員使用Fortran 編譯器對木材的本構模型進行自定義編輯，并利用Vumat 程序檢查本構模型是否存在錯誤。相關工作人員在該程序中輸入了21 種材料參數，并對其狀態變量進行定義，定義數量達到16 個（詳見表1）。

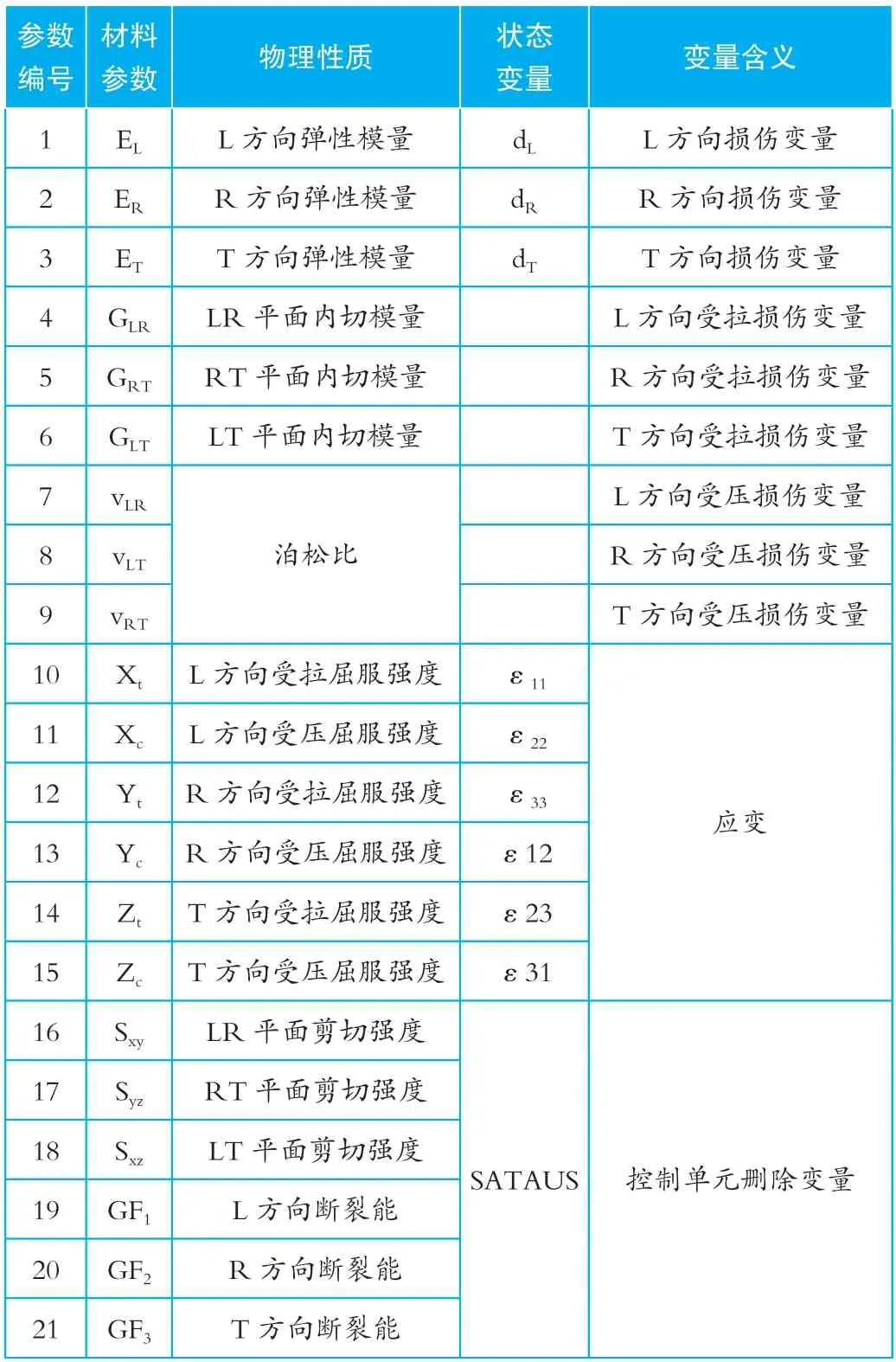
表1 VUMAT 材料常數

3 金屬結構性能參數計算

金屬結構臨時作業棚中的金屬結構以鋼材為主，本次試驗中用到的鋼材為Q235 薄壁型鋼，盡管鋼材受到的沖擊力屬于間接受力，是瞬態作用過程，但仍處于動力學范疇之內。因此在對材料進行定義的過程中，仍然需要加入應變率。設計人員根據Cower-Symonds 模型對鋼結構應變效率進行定義。

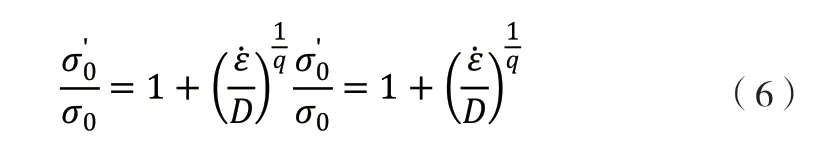
公式（6）中，σ表示鋼材的靜力強度，則表示鋼材在不同的塑性應變率（ε）下的動態強度數據。變量D 與q 均為計算參數，依據材料類型的不同，D 與q 也會發生變化。本次設計中，考慮到臨時作業棚鋼結構與碳素鋼的應變率相仿，因此將D 設定為40，q 為5 即可（詳見表2）。

表2 鋼材料性能參數

本次試驗中用到的臨時防護棚以木材作為主要材料構成頂端防護層，考慮到施工成本因素，以就地取材為原則，選擇木方與木模板作為防護層木材。木方使用花旗松，木模板采用楊木LVL。

4 建立有限元模型

4.1 施加約束力

金屬材料施工臨時作業棚所使用的鋼管，使用固接法進行連接，實驗中模擬高空墜物與作業棚的接觸點，僅需要計算垂直方向的位移數據，其他方向數據均設定為0。臨時作業棚上方設計有橫向空腹式防護結構，防護結構內部布置的木方以及木質模板，邊界條件選擇為開放狀態，并在高空墜物與作業棚接觸點，施加一個豎直方向的初始速度。

4.2 劃分網格

由于臨時施工棚使用的鋼材數量較多，且鋼材體積較大，因此使用S4R 網格進行建模。在實驗過程中，為了提升計算效率，可以將高空墜物簡化為一個離散剛體，在接觸到作業棚之后不會發生變形，其與作業棚只存在一個接觸點，該接觸點即為參考點，運用殼單元模型對剛性單元進行建模。針對作業棚中的木材，使用實體單元進行建模，并在計算機中構建3D 坐標系，對于木材的橫紋切向、橫紋徑向以及順紋進行標定，對應3D 坐標系中的Y、Z、X 軸。運用結構化劃分方式對木材進行網格化處理，利用8 節點線性縮減積分構建C3D8R 實體單元模型。

4.3 接觸分析

構建臨時施工棚有限元模型的主要目的，是計算高空墜物、鋼部件、木材之間的相互作用力。為了方便結算，該模型中的鋼部件使用Tie 型接觸進行約束，高空墜物與參考點之間使用coupling 約束條件，高空墜物與木方、鋼結構桁架之間采用Surface tu Surface 接觸模式，模型的切向使用庫倫摩擦，將摩擦系數設定為0.3。由于本次實驗中將高空墜物設定為離散剛體，木材的剛度小于高空墜物，因此將高空墜物設定為主面，木方與橫向空腹式桁架相比，其剛度較小，因此將橫向空腹式桁架作為另一個主面（如圖2 所示）。

圖2 臨時作業棚抗沖擊有限元模型

5 臨時作業棚抗沖擊性能分析

在分析臨時作業棚抗沖擊有限元時，要確保高空墜物在下落過程中其質量與形狀不發生變化。其墜落高度與沖擊性等價，作業棚受到沖擊之后其中心位置發生的形變最為明顯。因此，設計人員運用AVAQUS 軟件中的顯示分析模塊建立抗沖擊有限元模型，該模型一共44 個，能夠從木材厚度、沖擊力作用面積等方面驗證作業棚抗沖擊能力。

對于44 個有限元模型的抗沖擊能力進行分析之后，得到臨時作業棚橫向空腹式桁架以及木方的最大沖擊力，Mises 應力以及木方的破壞面積數據。

5.1 作用面積對臨時作業棚抗沖擊能力的影響

如果在金屬材料臨時作業棚頂端的橫向空腹式桁架內布置楊木LVL 或者花旗木，其作用面積與沖擊力有限元分析結果如下（如圖3 所示）。

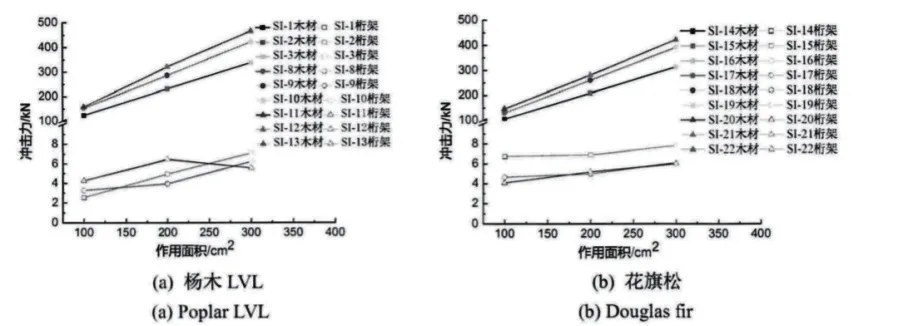
圖3 楊木LVL、花旗木作用面積與沖擊力有限元分析

通過分析圖3 可以發現：楊木LVL 在受到沖擊力之后，與墜物的接觸面積越大，其沖擊力越大。隨著作用面積擴大，在沖擊能量不變的情況下，楊木LVL 的位移與接觸面積呈反比例關系，作用面積越大楊木LVL 位移越小。木材位移的減少，意味著橫向空腹式桁架所受到的沖擊力變大，其位移增加。這種狀態下，楊木LVL 與桁架的Mises 應力以及破壞面積，也會隨著接觸面積增大而加大，沖擊造成的破壞以順紋剪切破壞為主。

如果將楊木LVL 替換為花旗松，沖擊作用面積越大，花旗木與桁架位移、Mises 應力變化越大。但由于花旗木厚度較大，具有很好的剛度，因此在受到沖擊力之后，高空墜落的物體會向反方向反彈，因此對于桁架的作用時間較短，桁架的位移變小。這種情況下，高空墜物對于木方的破壞以橫紋徑向破壞為主。

5.2 墜落高度對臨時作業棚抗沖擊能力影響

臨時作業棚橫向空腹式桁架中布置楊木LVL 或者花旗松木方，其作用面積與位移的有限元分析如下（如圖4 所示）。

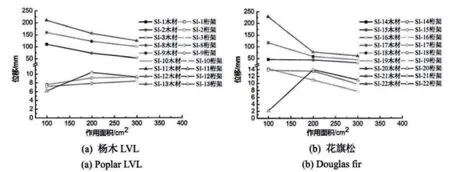
圖4 楊木LVL、花旗木作用面積與位移的有限元分析

通過分析圖4 可以發現：墜落高度越高，桁架與木方受到的沖擊力越大，木方的位移也越大。由于木材受到外力作用出現變形之后，對于高空墜物會起到一定的緩沖，因此墜物對于桁架的影響相對較小，桁架的位移也會逐漸減少。當墜物的高度較低，木方受到的破壞以順紋縱向剪切為主。如果墜物位置較高，則木材會徹底斷裂。

墜落物高度越高，花旗松木方移動越大，Mises 應力與墜落物高度成反比，其原因在于墜落物越高其下落的速度越快，木方受到沖擊之后以橫紋切向剪力破壞為主，木材吸收了大量的動能，使得桁架結構的位移變小，其受到的沖擊力也顯著降低，有利于保障桁架結構的完整性。

6 結語

工作人員利用ABAQUS有限元分析軟件，對金屬結構臨時作業棚抗沖擊能力進行了深入分析，通過模擬實驗分別論證了高空墜物的質量、墜落物高低以及木材厚度的變化以及對于臨時作業棚抗沖擊能力的影響，計算鋼結構、楊木LVL 以及花旗松木方在受到沖擊后的Mises應力變化情況、位移情況以及沖擊的破壞形式。通過實驗研究得出以下結論：

（1）墜落物作用面積越大、高度越高，其對于木方所造成的沖擊力越大，位移越明顯。同時木材能夠吸收的能量也越多，當木材無法抵消沖擊力就會被徹底擊碎，受到沖擊的時間也會相應變短。橫向空腹式桁架受到的沖擊力、位移以及Mises 應力與墜落物的作用面積、高度成反比關系，作用面積越大，桁架越穩定。

（2）在布置防護層時，可以采用厚度較大的木方，提升木方的剛性，確保木方能夠吸收大部分沖擊力。也可以采用單體面積較大的木質模板，通過均勻吸收沖擊力保證金屬結構的安全。在不影響施工進度以及成本的情況下，可以集中二者的優勢，選擇厚度較大且作用面積大的木方木質模板組合，提升臨時作業棚的抗沖擊能力。

（3）鋼結構桁架在受到沖擊之后，變形不明顯，沒有達到鋼構件的屈服強度，整個金屬結構體系能夠保證安全。