基于Hellinger距離的不平衡漂移數據流Boosting分類算法*

張喜龍，韓 萌，陳志強，武紅鑫，李慕航

(北方民族大學計算機科學與工程學院，寧夏 銀川 750021)

1 引言

從非平穩數據流中學習仍然是目前數據挖掘領域研究的重點，決策算法應該考慮到類別之間數量的不平衡性。真實的數據流還會表現出不斷變化的類不平衡比率，從而進一步影響分類性能。在數據流處理中，不平衡數據現象變得至關重要，因為它出現在各個領域，例如天氣數據預測、異常檢測和社交媒體挖掘等[1]。具有多數類數據的類別稱為多數類，而其它類別稱為少數類。

近些年隨著研究人員對不平衡數據的深入研究，集成學習與重采樣技術的結合屢見不鮮。Wang等[2]改進了基于在線的Bagging集成的過采樣OOB(Oversampling based Online Bagging)和欠采樣UOB(Undersampling based Online Bagging)算法。作者利用時間衰減度量對OOB和UOB 2種集成學習方法進行改進，以克服在線類不平衡問題。Wu等[3]提出了一個重要性采樣方法，即動態特征組加權框架用于對不平衡數據進行分類DFGW-IS(Dynamic Feature Group Weighting framework for classifying data Streams of Imbalanced distribution)。通過使用帶有子分類器的特征組進行加權集成去處理不斷變化的數據概念，其中子分類器通過它自身的分類性能和穩定性進行加權。為了解決概念漂移和類不平衡問題，Chen等[4]提出了遞歸集成方法REA(Recursive Ensemble Approach)。該方法有選擇地挑選以前的少數類實例加入當前訓練的塊，以平衡類分布，同時使用動態加權適應概念漂移。同時,Lu等[5]提出了一種基于塊的增量方法,稱為動態多數加權不平衡學習DWMIL(Dynamic Weighted Majority for Imbalance Learning)算法。該算法使用集成框架對基分類器動態加權，以處理帶有概念漂移和類的數據流不平衡問題。

盡管現有的集成分類算法能夠很好地處理類不平衡問題，但在不平衡數據流的集成分類中還存在很多問題有待解決。例如,如何解決帶有概念漂移的不平衡數據,基分類器如何分配合適的權值等。針對以上問題，本文提出了一種新的集成分類算法，主要工作如下所示：

(1)提出了一種新的基于Hellinger距離的Boosting集成加權算法BCA-HD(Boosting Classification Algorithm for imbalanced drift data stream based on Hellinger Distance)。算法采用實例權重和分類器權重組合的方法進行分類，首先使用Hellinger距離計算實例之間的權重，然后使用分類誤差計算分類器的權重，通過分類器的動態更新方式去適應不平衡數據流中的概念漂移。

(2)提出的BCA-HD算法在底層使用了集成算法SMOTEBoost(Synthetic Minority Oversampling TEchnique Boost)[6]作為動態更新的基分類器，該集成分類器通過重采樣的方式處理不平衡的數據，同時集成分類器在適應概念漂移方面比單分類器有著更好的魯棒性。

實驗表明，BCA-HD算法與典型的9種對比算法相比，它能更好地適應突變型和漸變型的概念漂移，同時對不平衡數據流分類性能也更好。

2 相關工作

2.1 不平衡數據流分類

隨著研究人員對不平衡數據研究的深入，它的解決方案也變得更加多元化。目前不平衡數據分類研究主要涉及數據重采樣和算法創新。

數據重采樣是通過丟棄一些多數類樣本(即欠采樣技術)或添加新的少數類樣本(即過采樣技術)來重新平衡類的分布[7]。在欠采樣技術方面，隨機欠采樣是最簡單的方法，它使用隨機方式丟棄多數類樣本。鑒于可能會去除一些有用的多數類樣本，研究人員設計了很多有效的欠采樣方法。在數據過采樣方面，最直接的方法是隨機過采樣，它隨機復制原始少數類樣本以引入少數類樣本。過采樣的一個顯著缺點是它會增加過度擬合的風險，為此研究人員提出了合成少數類樣本的過采樣技術即SMOTE[8]。在特征空間中生成合成樣本，通過在2個相鄰的原始少數類樣本之間進行插值，創建的新少數類樣本將不同于現有的少數類樣本。

在算法創新上集成學習是目前研究較多的方向之一，集成學習旨在通過組合多個基分類器來提高分類性能。由于其面向準確性的設計，標準集成學習算法不適合類不平衡學習。研究人員經常結合重采樣方法來開發基于集成的解決方案，以處理類不平衡問題。SMOTEBoost是第1個基于Boosting解決類不平衡問題的算法。在該算法中，SMOTE被嵌入AdaBoost.M2[9]的學習框架中，通過生成新的合成樣本來隱式增加少數類樣本的權重。最近Zyblewski等[10]提出結合動態集成和預處理技術的框架來處理高度不平衡的數據流，提出了使用分層Bagging分類器對少數類和多數類進行替換抽樣的方法。

2.2 概念漂移問題

在真實世界中，數據流的生成通常是在非平穩環境中進行，這意味著數據的底層分布可以隨時間任意更改。在這樣的非平穩環境中，數據流的概念和數據分布隨時間而變化，這種現象被稱為概念漂移[11]。下面從概率的角度來定義概念漂移，當2個時間點t0和t1的聯合概率發生變化時就會出現概念漂移，即pto(X,yi)≠pt1(X,yi)。

根據漂移變化的速度,概念漂移可分為突變、漸近、重復和增量漂移，如圖1所示。如果一種數據分布的來源被另一種數據分布的來源代替，稱為突變型。當開始觀察到兩種數據分布混合時，這種漂移被稱為增量型。當舊數據分布的數據實例開始減少，新數據分布的數據實例開始增加時，這種漂移被稱為漸變型。重復漂移是指新概念的實例或舊概念的實例在特定時間之后開始重復出現的情況[12]。在不平衡數據流中，概念漂移的體現已經簡化到了不平衡比率的變化隨著時間變化少數類或多數類轉變為多數類或少數類。

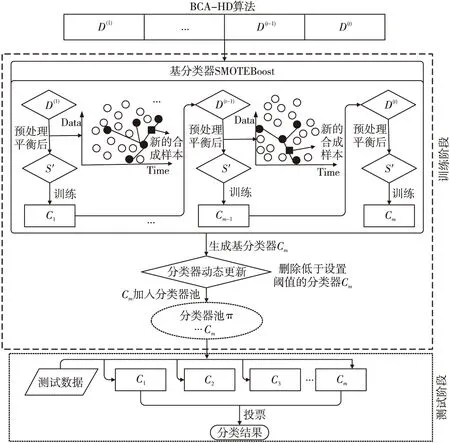
Figure 2 Illustration of BCA-HD圖2 BCA-HD示意圖

3 BCA-HD算法

通過對文獻的分析可以看出，不平衡數據流分類算法表現不佳，而且大多數工作沒有解決分類模型運行過程中可能出現的概念漂移問題。因此，所提出的解決方案應該對分類任務的參數變化具有很高的適應性，基于分類器集成方法是目前最受關注和研究較多的方向之一。同時，提出的解決方案應該考慮數據分布的局部特征和類之間的不平衡。

3.1 BCA-HD集成算法框架

在目前新的理論方面，Du等[13]提出了在線學習處理不平衡數據流的方法，通過改進在線Bagging技術來進一步提高分類性能。作者對少數類樣本和多數類樣本采用不同的泊松分布參數λ來區分樣本之間的采樣概率，以進一步平衡數據。在計算分類器的權重時，不是采用分類器的分類誤差而是用泛化誤差計算權重。該算法沒有考慮帶有概念漂移的不平衡數據流的處理，同時加權的方式是以分類器為主，在分類器的更新方面也沒有以動態的方式去實現整體更新。基于以上算法的啟發和分析，本文提出的算法考慮了概念漂移的存在，同時在加權方面引進了實例加權和分類器加權，以實現分類器的動態更新。

為了解決帶有概念漂移的不平衡數據流問題，本文提出了基于Hellinger距離的Boosting集成分類算法BCA-HD。該算法主要解決2大核心問題：概念漂移和不平衡，該集成算法框架處理數據的全部過程如圖2所示。算法在訓練階段，數據流以塊的形式輸入內存中，表示為S={D(1),…,D(t-1),D(t)},輸入的數據塊依次分配給當前集成分類算法SMOTEBoost，該算法將作為BCA-HD算法的基分類器來訓練數據。分類器內部采用經典的重采樣技術SMOTE，它使用差值方法來合成新的少數類樣本，以平衡當前的不平衡數據集生成新的平衡后的數據塊S′，然后使用當前分類器進行訓練。在概念漂移的處理方面，算法采用實例級和分類器級的加權組合方式，權重大小代表對當前概念的重視程度。算法的集成過程是一種分類器的動態更新方式，這個過程可以讓分類器更好地學習。隨著分類器的創建，如果當前分類器的權重沒有低于用戶設置的閾值將直接加入分類器池π，否則當前基分類器會被刪除，同時這個分類器會一直處于一種動態更新的過程。在測試階段，生成的集成分類器根據多數投票原則對輸入的數據進行預測分類。

3.2 BCA-HD算法訓練過程

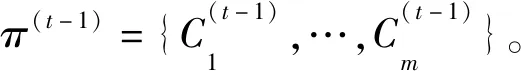
(1)

由于Hellinger距離公式對不平衡狀態下的數據具有不敏感性，BCA-HD算法使用該公式作為實例之間相似度的度量。這種相似度的度量對時刻發生概念變化的數據來說是一種友好的檢測方法，通過計算實例之間的距離權重然后分配給分類器來體現其對當前數據的重視程度。在分類器級，使用分類器的誤差來體現當前學習數據的好壞程度，從而能進一步更新分類器的權重，如式(2)所示：

(2)

(3)

(4)

其中，α為比例參數，當分類器池中的基分類器的更新權重低于閾值θ時，則進行刪除操作。如果要刪除分類器，一個原因可能是分類器是在一個非常早的時間上進行的訓練，先前訓練的基分類器無法對當前的數據概念進行擬合，它的誤差變大導致其權重會減小，表現在式(3)中總的求和權重降低。另一個原因是最近塊上數據的概念發生變化，使得分類器的測試誤差很大 ，導致權重變小被刪除。如果數據流非常長，則BCA-HD僅在集合中保留有限數量的分類器，而不會遇到存儲不夠的問題。分類器使用式(5)最終預測輸入的數據分布D(t)上的實例xi的分類結果。

(5)

其中，sign(·)為符號函數。

算法1是本文提出的BCA-HD集成分類算法的偽代碼，該算法是基于塊學習的方法,對于概念漂移有很好的適應性。

算法1BCA-HD

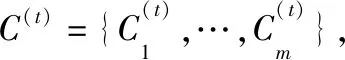
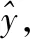
步驟1傳入數據流S;

步驟3創建基分類器C；//(call算法2)

C←SMOTEBoost(D(t))，π←{C};

步驟4fori←1 toNdo//遍歷實例

步驟5使用當前集成分類器C(t)預測實例xi;

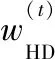
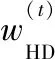
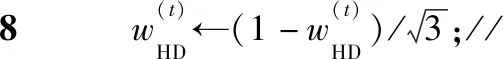
步驟9else取所有實例權重的平均值

步驟10forj←1 tomdo//遍歷分類器

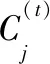
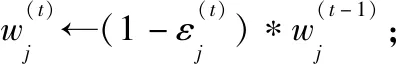
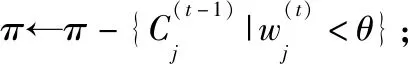
步驟16m←|C(t)|；

步驟17創建新的基分類器：

C←SMOTEBoost(D(t))//call算法2

步驟18m←m+1;

步驟19π←π∪{C};

步驟21endif

步驟22endfor

步驟23 endfor

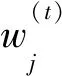
3.3 不平衡數據的處理

在分類器的創建上使用了集成分類算法作為BCA-HD算法的基分類器。SMOTEBoost算法是一個很健壯的算法，該算法數據采樣部分使用SMOTE重采樣技術處理不平衡數據。SMOTEBoost的偽代碼如算法2所示。

算法2SMOTEBoost

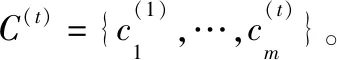
輸出：輸出集成分類器C。

步驟1D1(i)=1/N,i=1,…,N;//初始數據分布。

步驟2 forj←1 tomdo//遍歷分類器

步驟3采用SMOTE算法合成少數類，生成新的訓練集S′；

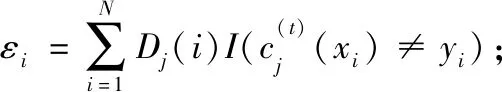
步驟6fori←1 toNdo

步驟7遍歷實例來更新分類器誤差：

步驟8endfor

步驟9endfor

步驟10輸出最終的集成分類器C。

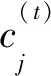
4 實驗設置

4.1 實驗數據集

在實驗中，本文采用了6個人工數據集和2個真實數據集來驗證本文算法。其中Drifting Gaussian、Moving Gaussian、SEA、Hyper Plane、Spiral和Checkboard人工數據集使用概念漂移生成器生成;2個真實數據集為Electricity[15]和Weather[15]。Electricity數據集包含了澳大利亞新南威爾士州時間和需求的電價，類標簽是通過過去24小時的價格變化情況來確定。Weather數據集包含美國貝爾維尤和內布拉斯加州超過50年的天氣信息，任務是預測某一天是否會下雨。具體的數據集特征如表1和表2所示。本文算法主要以二元分類為主，為了更好地研究帶有概念漂移的不平衡數據流，數據集會分為突變型(Abrupt)和漸變型(Gradual)2種漂移類型的數據,如表1和表2所示。

Table 1 Abrupt datasets表1 突變型數據集

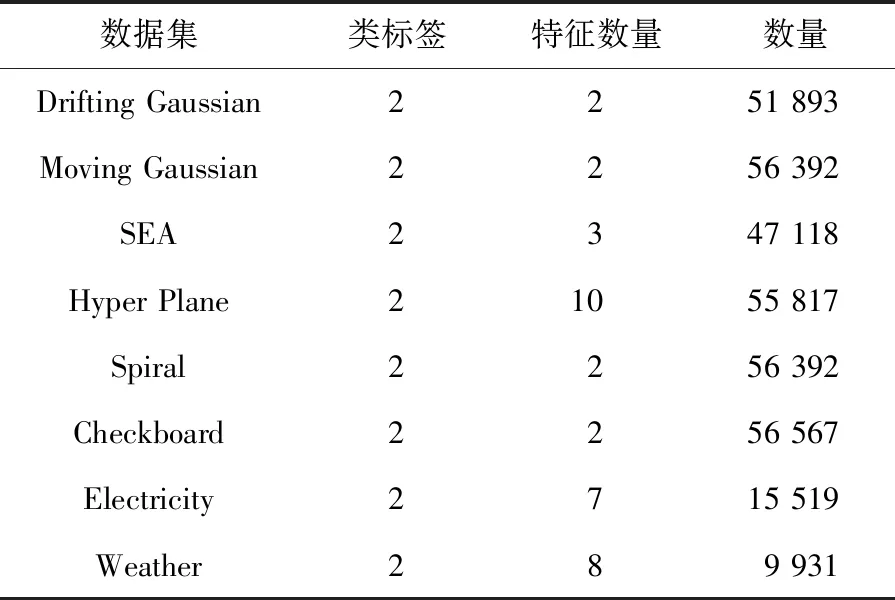
Table 2 Gradual datasets表2 漸變型數據集

為了模擬真實的數據流中概念漂移變化的情況，實驗通過不平衡比率的動態變化來模擬漂移的發生。

(1)突變型概念漂移：不平衡比率初始設置為0.01,數據流產生過半時，不平衡比率突變成0.99,也就是多數類變成了比率只有0.01的少數類。

(2)漸變型概念漂移：不平衡比率初始設置為0.01,在產生1/3的數據流后，不平衡比率不斷增大，直至數據流量到達最大時，不平衡比率達到了0.99。

4.2 算法評估指標

在類不平衡數據流中，傳統的指標已經不適用不平衡的場景，分類器總傾向多數類別，因此針對不平衡分類性能評估，相關學者提出了常用的F-measure和G-mean等以評價分類器對于多數類和少數類樣本的分類性能。G-mean是由Kubat等[16]提出的幾何均值，常被應用于不平衡類標簽屬性的數據流所在的領域。G-mean用表3所示的混淆矩陣來定義,其計算如式(6)所示：

(6)

Table 3 Confusion matrix表3 混淆矩陣

受試者工作特征曲線ROC(Receiver Operating Characteristic)和AUC(Area Under ROC Curve)是常用的評估分類器性能的指標。其中AUC是ROC曲線下的面積，AUC越接近1，表示該分類器性能越好。本文采用G-mean和AUC作為BCA-HD算法的性能評價指標。

4.3 實驗環境

為了驗證BCA-HD算法的性能，本文將BCA-HD算法與9種對比算法應用于突變型和漸變型數據集，然后比較其G-mean和AUC。本次實驗的硬件環境是Intel Core i5 1T+128 MB RAM的PC機，操作系統是Windows 10專業版，編程語言為Python3.6。

5 實驗結果分析

5.1 塊大小對BCA-HD算法的影響

BCA-HD是基于塊實現的集成分類算法，因此塊的大小直接影響算法的執行效果。為了驗證塊大小對算法的影響，實驗分別將數據塊大小設置為d=500，750，1 000，1 250，1 500，1 750和2 000。其中d表示一個塊所包含實例的數目。算法在Abrupt和Gradual 2種類型數據集上運行，實驗結果使用G-mean指標展示，如表4和表5所示。

表4給出了在突變型數據集上不同塊大小算法的G-mean性能。整體看初始隨著塊大小的增長G-mean值也在不斷增長，當d=1 000時除了Spiral數據集外其余7個數據集上的G-mean都開始下降,說明隨著塊大小的增大，不平衡比率也都在不斷變化，使得分類器適應它的能力變差。但是,在d=1 750時,G-mean開始緩慢增長，Drifting Gaussian和Hyper Plane在d取值為1 750和2 000時分別增長了2.14%和1.54%,說明分類器開始適應突變數據流，其中SMOTEBoost算法作為基分類器由于采用了SMOTE的重采樣技術可以很好地平衡數據流。

表5是漸變型數據集上的運行結果，從整體看除了Drifting Gaussian和Moving Gaussian數據集上G-mean的性能下降較快外，其余的保持了平穩的增長狀態。其中在真實數據集Weather上，在d取值為1 000和1 500時指標增長了7.63%，在Spiral數據集上,在d取值為1 000和1 250時指標增長了6.66%,說明數據流的塊大小在緩慢變化情況下并不影響分類器的訓練。其中在2種類型數據集上d=2 000時，分類器的表現均出現了下滑，說明塊大小不能無限度地增大。在2種類型數據集上表現最好的G-mean使用粗體標了出來。

5.2 基分類器數量對BCA-HD算法的影響

本文提出的BCA-HD是集成分類算法，它是由基分類器組合形成的，因此很有必要探究基分類器的數量對算法的影響。實驗設置分類器的數量在[1,15]內變化，BCA-HD算法在突變型和漸變型數據集上的G-mean如表6和表7所示。為了更好地展現數據的變化情況，給出了如圖3和圖4所示的箱線圖，其縱坐標是G-mean值的均方差。例如,在Electricity數據集上在分類器數量在[1,15]內的G-mean平均值為0.674 2，當分類器為1時均方差為+0.003 9。

Table 4 G-mean of different algorithms on abrupt datasets with different chunk sizes 表4 不同數據塊大小時不同算法在突變型數據集上的G-mean

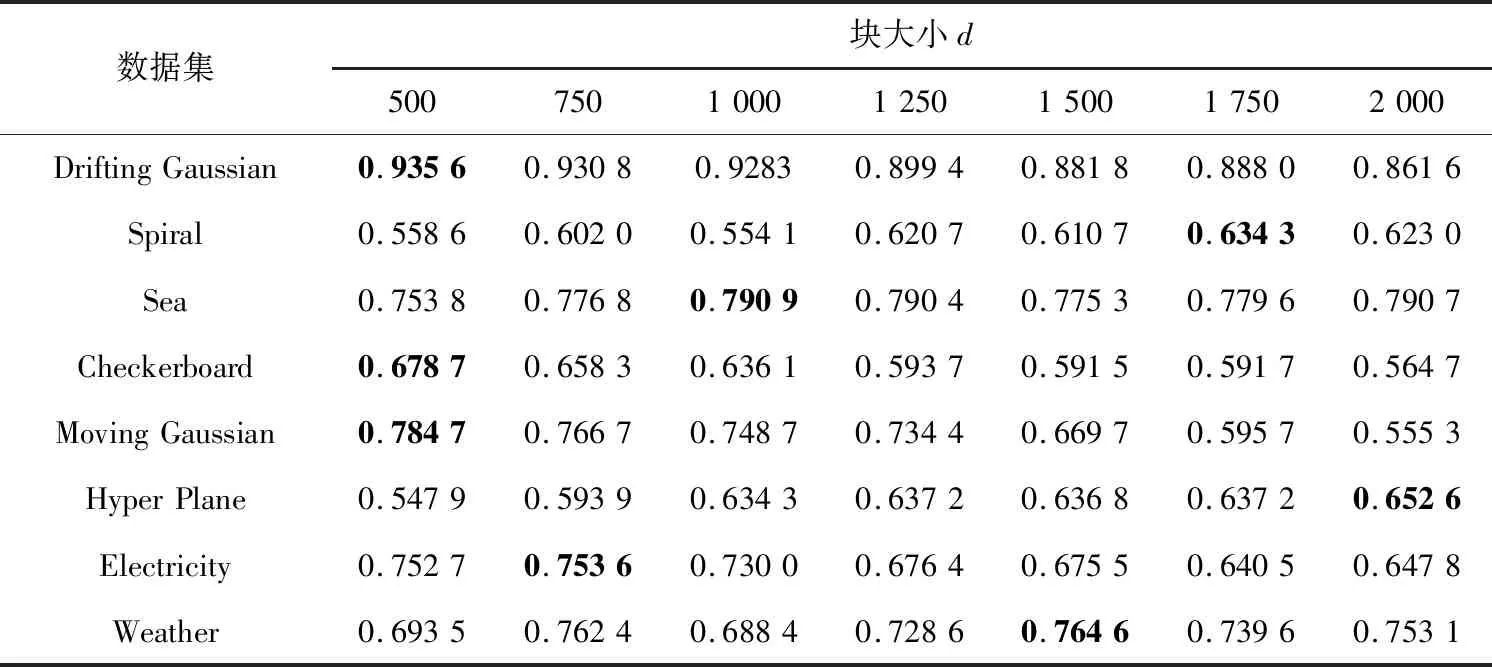
Table 5 G-mean of different algorithms on gradual datasets with different chunk sizes表5 不同數據塊大小時不同算法在漸變型數據集上的G-mean

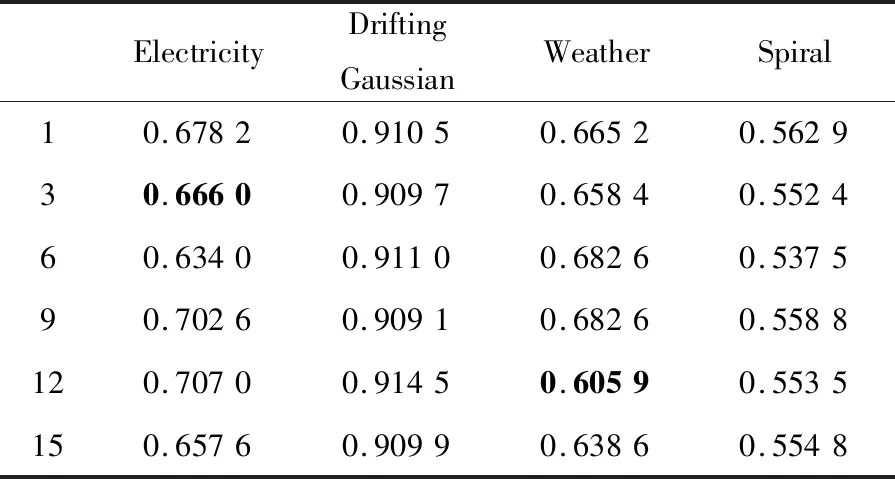
Table 6 G-mean of different algorithms on abrupt datasets when the number of base classifiers varies表6 不同基分類器數量時不同算法在突變型數據集上的G-mean

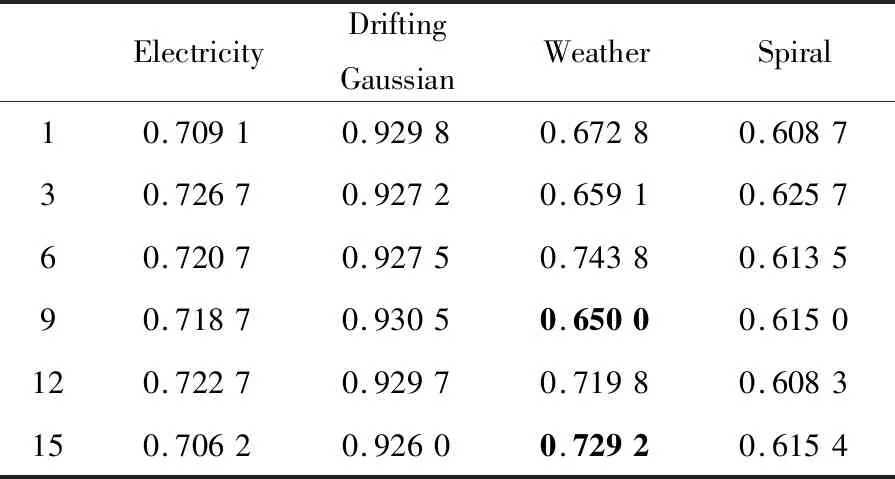
Table 7 G-mean of different algorithms on gradual datasets when the number of base classifiers varies表7 不同基分類器數量時不同算法在漸變型數據集上的G-mean

Figure 3 G-mean of different algorithms on abrupt datasets when the number of base classifiers varies圖3 不同基分類器數量時不同算法在突變型數據集上的G-mean

Figure 4 G-mean of different algorithms on gradual datasets when the number of base classifiers varies圖4 不同基分類器數量時不同算法在漸變型數據集上的G-mean

圖3展示了在突變型數據集上分類器數量由1～15的變化情形。分類器數量在[1,3]時，均方差的變化是±0.01；在[6,12]時，隨著分類器數量的增加均方差的變化在±0.04。均方差整體處于一種正增長，說明分類器數量的增多可以更好地適應突變型概念漂移。圖3中的圓點是異常點，在表6中用黑體字標示了。

圖4展示了漸變型數據集上的實驗結果。從圖4中可以看到,隨著分類器數量的增加，整體的G-mean值均方差變化控制在±0.02左右,說明隨著分類器數量的增加，分類器的性能趨于一種穩定的狀態。漸變型數據集對分類器的影響較小，圖4中的圓點是異常點,在表7中用黑體字標示了。

5.3 BCA-HD算法性能對比分析

為了驗證BCA-HD的分類性能，本文使用基于塊和在線的9種算法進行比較。基于塊的算法有ACDWM(Adaptive Chunk-Based Dynamic Weighted Majority)[15](采用了塊大小不固定的形式適應概念漂移同時采用重采樣技術平衡數據集)、Learn++.NIE[16](在每個塊上創建分類器進行訓練)、DWMIL[5]、REA[4]和DFGW-IS[3]。基于在線的算法有：HLFR (Hierarchical Liner Four Rates)[18]、DDM-OCI (Drift Detection Method-Online Class Imbalance learning)[19]、PAUC-PH (Prequential Area Under the ROC curve Page-Hinkley)[20]和OOB[2]算法,前3個算法是不平衡數據的漂移檢測算法。以上算法的數據塊大小d=1 000，基分類器個數設為12，損失函數為G-mean。實驗結果如表8～表11所示。其中對比算法在每個數據集上的性能指標大小進行了排名(括號里面進行了標注)，最好的指標使用黑體字進行了標注，同時Average Rank展示了每個算法的平均排名。

表8和表9列出了對比算法在突變型數據集和漸變型數據集上的G-mean值。由表8可知，BCA-HD算法在5個突變型數據集上的G-mean值高于其他對比算法的。其中在Drifting Gaussian數據集上本文算法的G-mean值分別比DMWIL、OOB算法高2.99%,10.12%;BCA-HD算法在Checkboard數據集上位于第2名，與DWMIL算法相差0.08%。在表9中，BCA-HD算法在7個漸變型數據集上取得了第1名，其中在Hyper Plane數據集上高于ACDWM算法3.92%。

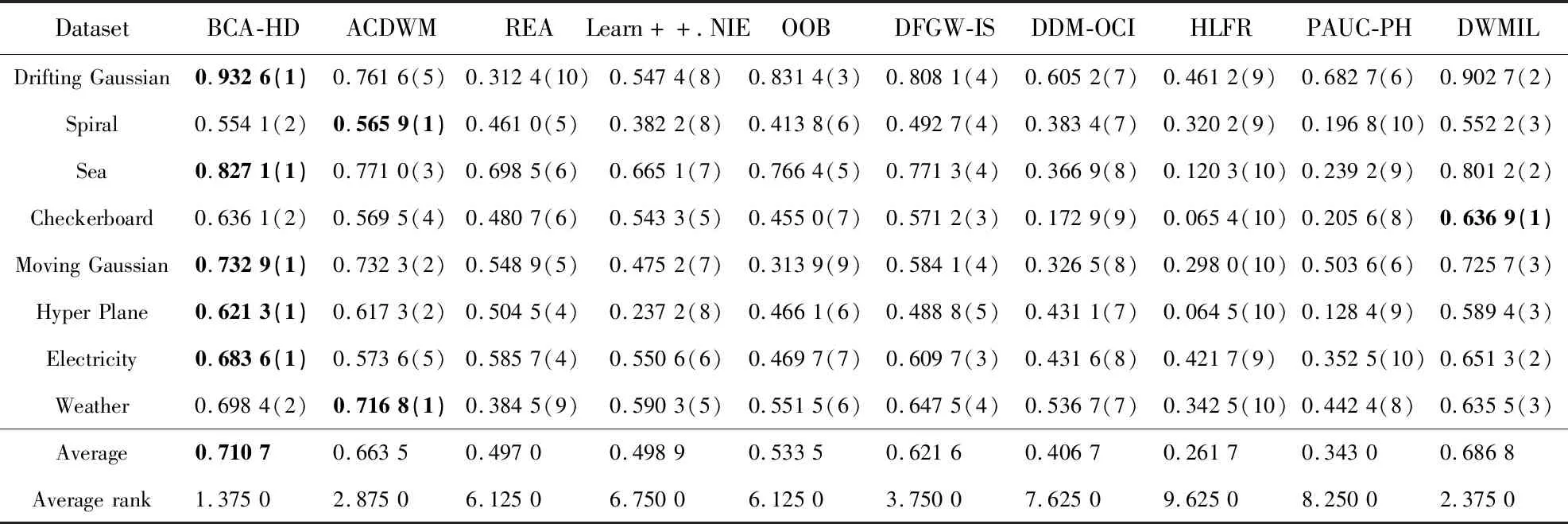
Table 8 G-mean of different algorithms on abrupt datasets表8 不同算法在突變型數據集上的G-mean值

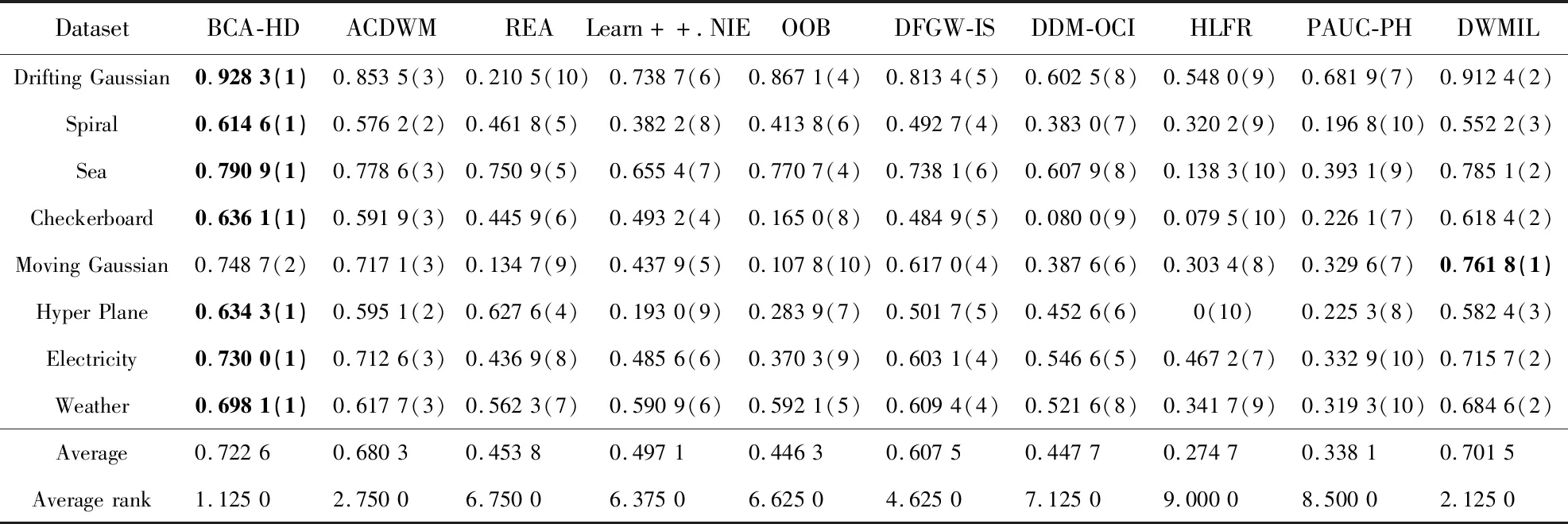
Table 9 G-mean of different algorithms on gradual datasets表9 不同算法在漸變型數據集上的G-mean值

表10和表11展現的是各算法在2種類型數據集上的AUC。從表10可知，本文算法在5個突變型數據集上的AUC高于其它對比算法的，其中在Drifting Gaussian數據集上，BCA-HD的AUC是91.96%,高于所有對比算法的；在Moving Gaussian和Checkboard數據集上取得了第2名和第3名，并且在這2個數據集上的結果與第1名分別僅相差1.35%和0.96%。在表11中，BCA-HD在6個漸變數據集上的AUC取得了第1名，其中在Moving Gaussian與第2名相差最大,為2.36%，而在Sea數據集上低于第1名0.73%。

為了更詳細地對比不同算法的性能，圖5和圖6給出了不同算法的G-mean和AUC對比情況。在圖5a中給出的是在8個突變型數據集上的G-mean和AUC平均值的對比情況，BCA-HD在2種評估指標上都是趨于持平狀態,說明隨著不平衡比例的不斷變化本文提出的算法可以很快適應概念漂移的發生。而HLFR算法的G-mean和AUC平均值相差較大，雖然該算法可以檢測概念漂移的存在，但是又無法快速處理變化的不平衡數據流。在圖5b中BCA-HD算法的平均排名是第1名，緊跟其后的便是DWMIL算法,這是由于其底層使用了處理不平衡的欠采樣算法和動態更新機制，因此能很好地適應數據流的變化。圖6a和圖6b是漸變型數據集上各算法2種指標的平均值和平均排名，可以看到BCA-HD是10種算法中分類性能最好的，具體表現為其G-mean和AUC值高，排名也最高，這表明在漸變狀態下的不平衡數據流集成算法依然可以很好地處理變化微小的數據。同時,基于塊的ACDWM、Learn++.NIE、DFGW-IS和DWMIL算法也有很平穩的適應性，這與它們各自使用的平衡數據流機制有關。

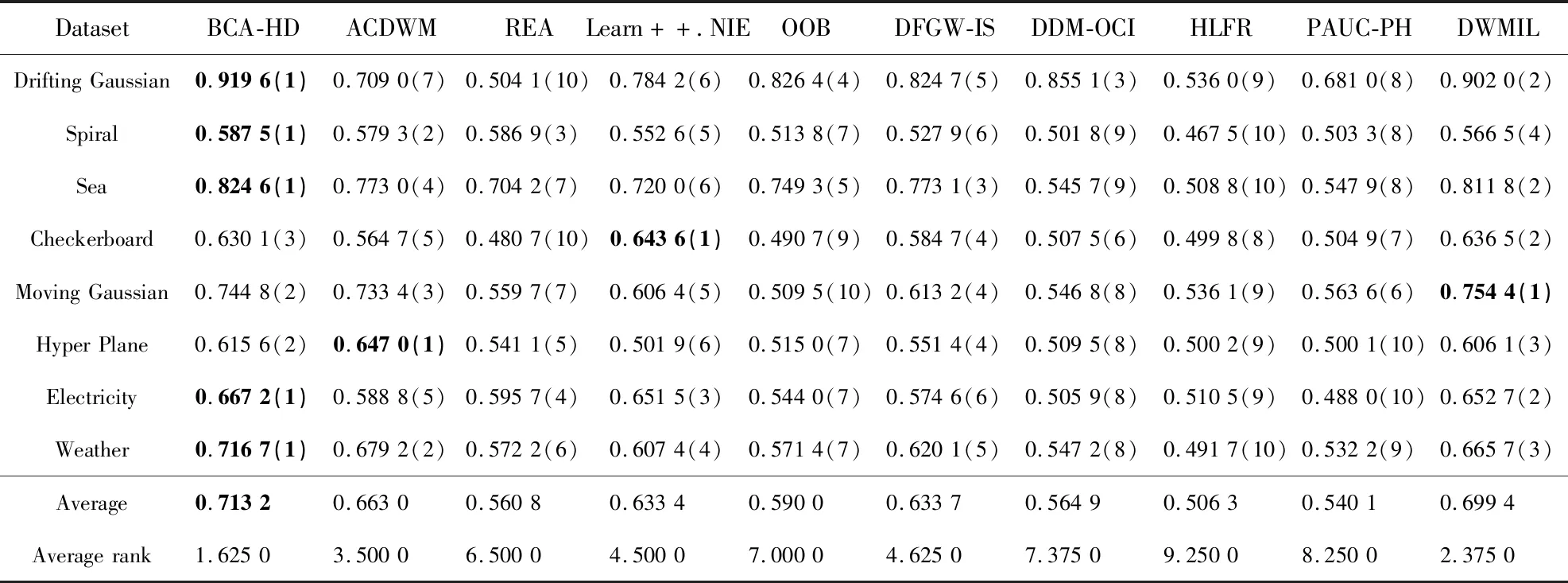
Table 10 AUC of different algorithms on abrupt datasets表10 不同算法在突變型數據集上的AUC值

Table 11 AUC of different algorithms on gradual datasets表11 不同算法在漸變型數據集上的AUC值

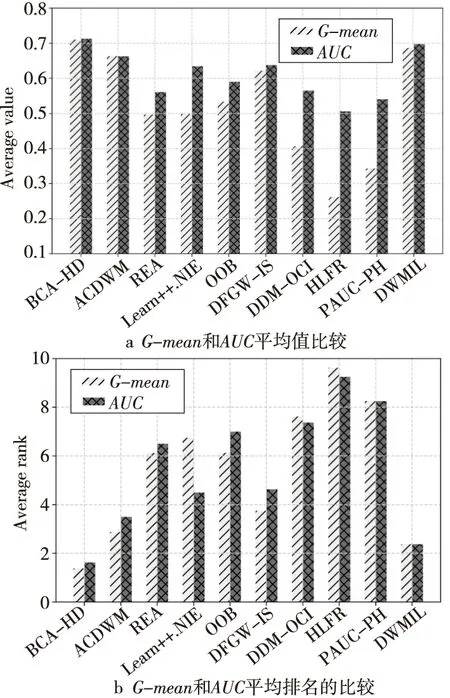
Figure 5 Comparison of G-mean and AUC of different algorithms on abrupt datasets圖5 不同算法在突變型數據集上的G-mean和AUC對比

5.4 BCA-HD算法參數與時間效率分析

本文提出的BCA-HD算法是基于Hellinger距離的集成加權算法，由于算法是基于實例級和分類器級的組合加權，因此主要使用2種參數，即權重組合參數α和刪除分類器的閾值參數θ。實驗中2種參數的取值分別在[0.1,0.5]內，實驗的結果如表12和表13所示。

表12和表13是在5個突變型數據集上的實驗結果。從圖7中可以看到，整體隨著α的增加均方差的變化范圍在±0.02，其中α=0.2時均方差變化超過±0.03，說明α的取值為0.02較為合適。圖7中圓點是異常點,在表12用黑體字標注出來了。在圖8的箱線圖中，整體θ的增加使均方差變化在±0.02內，但是負增長的比較多。說明隨著閾值θ的增大無法刪除更多的分類器，動態更新變得緩慢，適應概念漂移的能力開始下降。

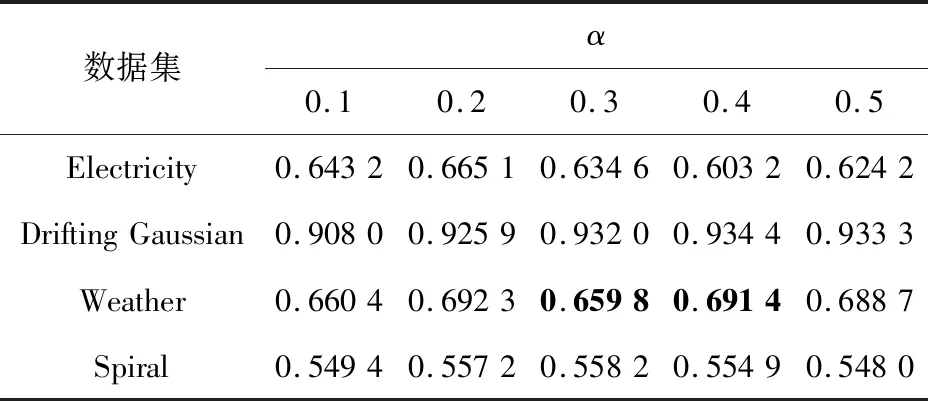
Table 12 G-mean of BCA-HD when α=0.1～0.5表12 α=0.1～0.5時BCA-HD 的G-mean

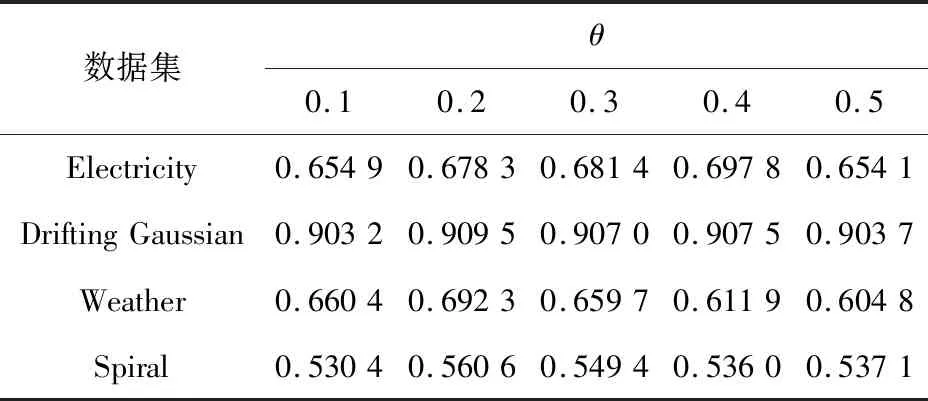
Table 13 G-mean of BCA-HD when θ=0.1～0.5表13 θ=0.1～0.5時BCA-HD 的G-mean

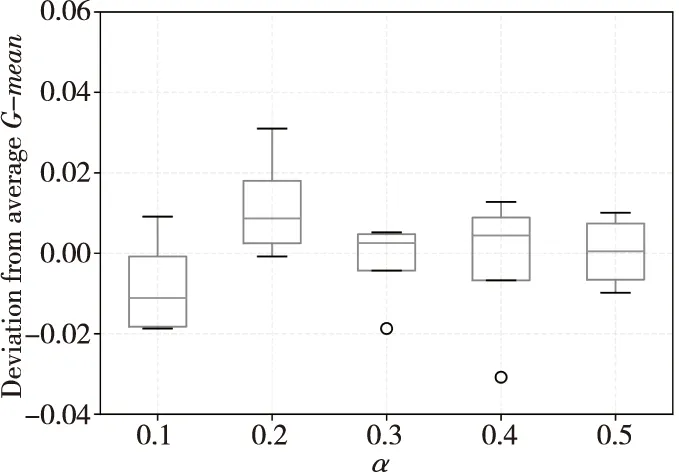
Figure 7 Comparison of deviation from average G-mean of BCA-HD when α=0.1～0.5圖7 α=0.1～0.5時BCA-HD的G-mean均方差比較

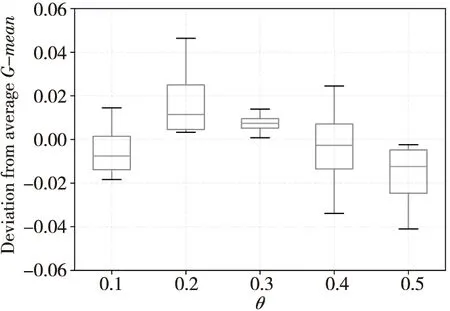
Figure 8 Comparison of deviation from average G-mean of BCA-HD when θ=0.1～0.5圖8 θ=0.1～0.5時BCA-HD的G-mean均方差比較

為了實驗的完整性，本文還在真實數據集上分析了BCA-HD算法的時間效率,結果如圖9和10所示。從圖9和圖10中可以看到,BCA-HD算法的運行時間是在不斷地上升，這是由于算法使用了實例級和分類器級的加權,增加了計算復雜度。其中DWMIL和HLFR算法的時間也處于一種線性增長態勢，這是因為它們分別使用了動態加權和概念漂移的檢測機制，從而增加了計算時間。

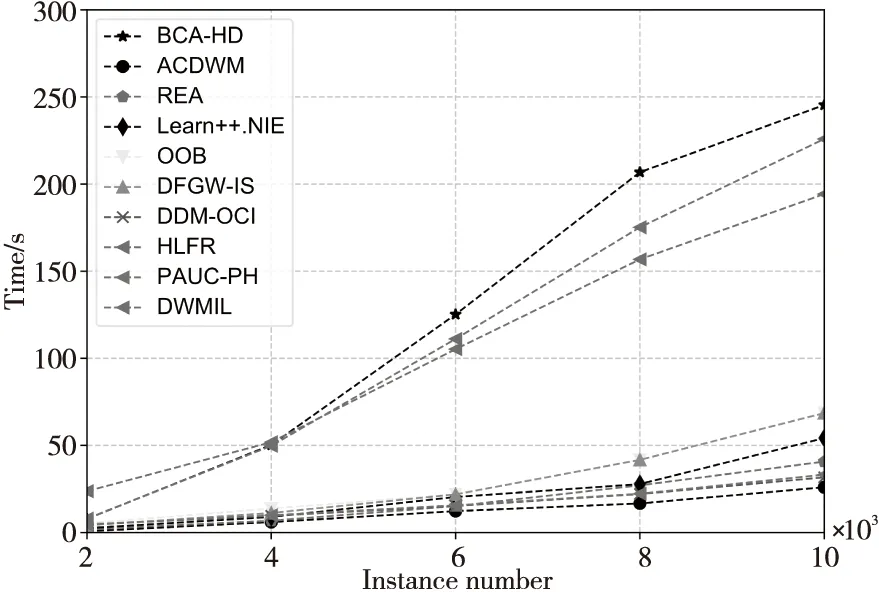
Figure 9 Comparison of algorithm running time on Weather圖9 Weather上的算法運行時間對比

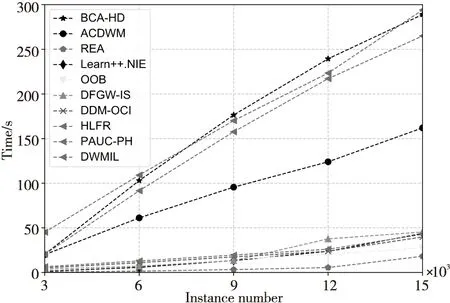
Figure 10 Comparison of algorithm running time on Electricity圖10 Electricity上的算法運行時間對比

6 結束語

本文首先闡述了不平衡數據流分類和概念漂移的基本概念,并對已有算法進行了概述；隨后提出了一種新的基于Hellinger距離的集成加權分類算法BCA-HD用于處理帶有概念漂移和不平衡問題的數據。對比分析實驗顯示，本文所提出的算法具有較好的優勢，并得出了以下結論：

在突變型和漸變型數據集上，隨著塊的增大算法性能會先下降然后再逐漸回升，說明該算法可以較好地適應塊大小的變化。在基分類器數量的實驗中，算法在漸變型數據集上隨著分類器數量的增加變化趨于穩定，而在突變型數據集上有明顯變化，說明在突變情況下受分類器數量影響較大。在對比實驗中，相比經典的不平衡算法,本文提出的算法取得了更優的性能，說明BCA-HD算法能很好地適應漸變型和突變型概念漂移和不平衡的發生。

本文所提出的算法為二元不平衡分類問題提供了有效的解決方案。但是,組合加權的方式增加了計算復雜度,消耗了更多的時間。后續的研究將會在算法的基分類器數量的剪枝策略入手以降低時空復雜度。