廣義二次矩陣的廣義多項式秩不變性

陳梅香, 楊忠鵬, 林志興, 馮曉霞

(1. 莆田學院 應用數學福建省高校重點實驗室, 福建 莆田 351100；2. 閩南師范大學 數學與統計學院, 福建 漳州 363000)

0 引 言

廣義二次矩陣[1]是二次矩陣的推廣[2-6], 目前關于廣義二次矩陣的研究已有很多結果[7-22]. 設n×n,[x]分別為復數域上的n×n階矩陣集合和一元多項式集合,r(A)為A∈n×n的秩,I(Ir)為r×r階單位矩陣,+為正整數集合.約定Ψn={P∈n×n|P2=P}.如無特殊說明, 本文的矩陣P均為冪等矩陣, 即P∈Ψn.若存在d,e∈, 使得(A-dI)(A-eI)=0, 則稱A∈n×n為由d,e確定的二次矩陣.若

A2=αA+βP,P2=P∈Ψn,AP=PA=A,α,β∈,

(1)

則A稱為(由冪等矩陣P和α,β∈確定的)廣義二次矩陣[1], 且記

Ωn(P)={A∈n×n|A2=αA+βP;α,β∈,AP=PA=A}.

(2)

文獻[15,20-22]使用了定義式(1), 還可以使用如下定義：

Ωn(P;d,e)={A∈n×n|(A-dP)(A-eP)=0,AP=PA=A},

(3)

其中P∈Ψn.當P=I時, 式(3)即為由d,e確定的二次矩陣.由式(1)～(3)易得:

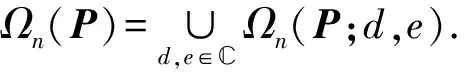
(A-dP)(A-eP)=A2-αA-βP=0,

(4)

其中

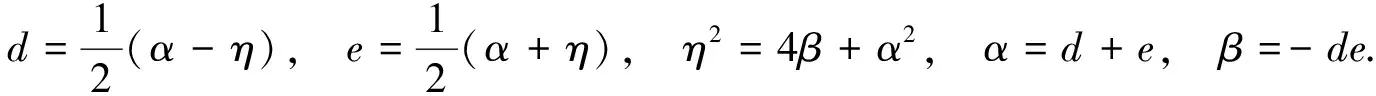
(5)

由命題1知, 式(3)與式(1)廣義二次矩陣的定義等價.

命題2[1]設P∈Ψn,A∈Ωn(P;d,e),k∈+, 則Ak∈Ωn(P),

Ak+1=αkA+βkP,

(6)

其中α1=α,β1=β且αk+1=ααk+βk,βk+1=βαk.

文獻[7]將命題2推廣到廣義二次算子上.文獻[1]用歸納法, 由式(1)出發比較了Ak+1=AAk與Ak+1=αkA+βkP中A,P對應的系數, 得到了αk,βk的計算公式(6).本文延續文獻[1]的結論和研究方法.

對任意一組復數am,…,a1,a0, 文獻[1]考慮了A∈Ωn(P)的多項式：

fP(A)=amAm+…+a1A+a0P,

(7)

這里f(x)=amxm+…+a1x+a0∈[x],m∈+.

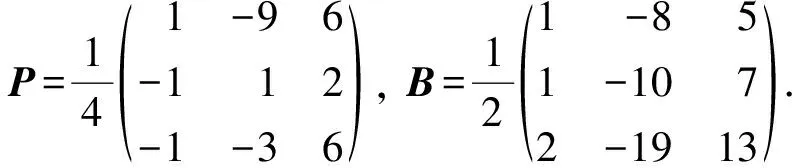
例1表明, 文獻[1]給出的廣義二次矩陣多項式(7)與通常意義下的矩陣多項式不同.因此文獻[11]稱式(7)中的fP(A)為A的廣義多項式合理.

命題3[1]設P2=P∈Ψn,A∈Ωn(P)滿足式(1),f(x)由式(7)確定, 則

fP(A)=α*A+β*P∈Ωn(P),

(8)

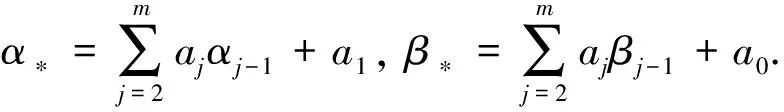
式(8)表明, 廣義二次矩陣A的fP(A)對Ωn(P)的運算是封閉的, 且fP(A)作為A與P的線性組合系數, 可由式(8)得到, 并與多項式f(x)有關.對給定的p,q∈, 總設

Γ(p,q)={(a,b):ab(ap+bq)≠0,a,b∈},

特別地,Γ=Γ(1,1).由文獻[23-24]可知, 對線性算子Fredholm穩定性質的研究有一定的理論意義.

命題4[25-26]設P,Q∈Ψn, 則r(aP+bQ)=r(P+Q), (a,b)∈Γ.

命題5[27-28]設P,Q,A,B∈n×n, 則

r(PQ-QP)=r(P-Q)+r(I-P-Q)-n=r(PQ-PQP)+r(PQP-QP),

(9)

r(AB-BA)=r(A+B)+r(A-B)-n,

(10)

其中P2=P,Q2=Q,A2=B2=I.

本文根據文獻[22], 利用A∈Ωn(P;d,e)與冪等矩陣P的關系, 證明廣義二次矩陣可表示為兩個冪等矩陣的線性組合, 并討論廣義二次矩陣中廣義多項式的基本性質及其運算的秩不變性.結果表明, 廣義多項式的秩不僅與組合系數的選擇無關, 而且在大多數情況下與多項式的選擇也無關.從而概括并推廣了已有冪等矩陣、 對合矩陣、 二次矩陣、 廣義二次矩陣的相關結果.

1 預備知識

引理1設P∈Ψn,AP=PA=A.如果d,e∈且d≠e, 則

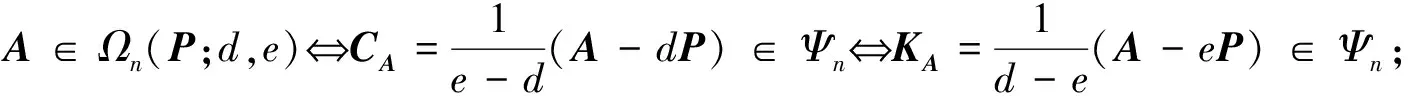
(11)

且當A∈Ωn(P;d,e)時,

A=(e-d)CA+dP=(d-e)KA+eP,PCA=CAP=CA,PKA=KAP=KA,

(12)

A=eCA+dKA,CA+KA=P,CAKA=KACA=0.

(13)

證明: 當A∈Ωn(P;d,e)且d≠e時, 由式(3)知(A-dP)(A-eP)=0, 則

當A∈Ωn(P;d,e)時, 由式(11)可得(e-d)CA+dP=(A-dP)+dP=A, 又由AP=PA=A可知,

同理可得A=(d-e)KA+eP且PKA=KAP=KA.因此式(12)成立.當A∈Ωn(P;d,e)時, 由式(11)可得

結合式(3)得

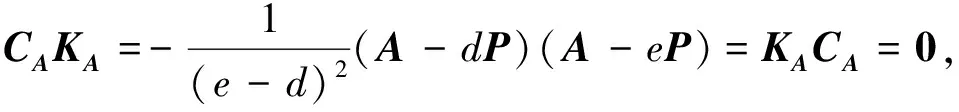
(15)

即式(13)成立.證畢.

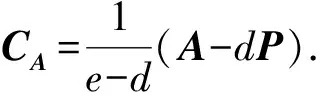
引理2設P∈Ψn,A∈n×n且AP=PA=A, 則有可逆矩陣G和W, 使得

P=Gdiag(Ir,0)G-1,r(P)=r；A=Gdiag(A1,0)G-1,A1∈r×r；

(16)

A∈Ωn(P;d,e)?A1∈Ωr(Ir;d,e).

(17)

當d≠e時,

A=Wdiag(dIt,eIr-t,0)W-1∈Ωn(P;d,e),P=Wdiag(Ir,0)W-1.

(18)

證明: 由文獻[14]中引理9或文獻[16]中定理1.1及文獻[21]中引理1的證明知, 式(16)成立.從而

(A-dP)(A-eP)=Gdiag((A1-dIr)(A1-eIr),0)G-1,AP=PA=A.

故由式(3)得式(17).由文獻[16]中定理1.1(iii)的證明或文獻[20]中引理3的(9)得式(18).證畢.

對?f(x)∈[x]形如式(7), 當P∈Ψn,r(P)=r,AP=PA=A時, 由式(16),(17)可得

fP(A)=amAm+…+a1A+a0P=Gdiag(f(A1),0)G-1,

(19)

其中A1∈r×r.文獻[16,19]中研究的廣義二次矩陣是由同一個冪等矩陣確定的, 本文討論更一般的情形.約定： 若P,Q∈Ψn, 則A∈Ωn(P;dA,eA),B∈Ωn(Q;dB,eB), 且對f(x),g(x)∈[x], 設

ω=ω(A,B)=(eA-dA)(eB-dB),ωf,g=(f(eA)-f(dA))(g(eB)-g(dB)).

(20)

將文獻[8]中定理2和文獻[9]中定理3.2應用到有限維空間, 可得:

引理3設P,Q∈Ψn,A∈Ωn(P),B∈Ωn(Q)滿足A2=αAA+βAP,βA≠0, 且B2=αBB+βBQ,βB≠0.如果P-Q可逆, 則A-B可逆.

引理4設P∈Ψn,A∈Ωn(P;dA,eA),B∈Ωn(P;dB,eB)且dA≠eA,dB≠eB.則

r(CACB-CBCA)=r(CA1CB1-CB1CA1)=r(AB-BA).

(22)

當dA=dB=d≠e=eA=eB時,

r(AB-BA)=r(A-B)+r[(e+d)P-A-B]-r(P).

(23)

當A∈Ψn,B∈Ωn(I;0,μ)時,

r(AB-BA)=r(AB-ABA)+r(ABA-BA).

(24)

證明: 式(21)可由文獻[12]中定理3.1的式(3.1),(3.4)得到, 式(22)來源于文獻[12]定理3.1證明中的式(3.6), 式(23)即為文獻[12]中定理4.1, 式(24)可由文獻[12]中式(4.4)得到.證畢.

2 廣義二次矩陣的廣義多項式

定理1設P∈Ψn,A∈Ωn(P;d,e), 則當d≠e時,

Ak=(ek-dk)CA+dkP,k∈+；

(25)

當d=e時,

Ak+1=(k+1)dkA-kdk+1P,k∈+;

(26)

且

Ak∈Ωn(P;dk,ek),k∈+.

(27)

證明: 當d≠e時, 用歸納法證明式(25).當k=1時, 由式(11)知式(25)成立.假設當k-1≥1時, 式(25)成立, 即有Ak-1=(ek-1-dk-1)CA+dk-1P, 則由式(11)有

即式(25)成立.

當d=e時, 由式(3)知當k=1時式(26)成立, 且A2=2dA-d2P,A∈Ωn(P;d,d)； 而

A3=2d(2dA-d2P)-d2A=3d2A-2d3P,

即當k=2時式(26)成立.假設k-1≥2時式(26)成立, 即

Ak=A(k-1)+1=kdk-1A-(k-1)dkP,

則

Ak+1=AkA=kdk-1(2dA-d2P)-(k-1)dkA=dk[2k-(k-1)]A-kdk+1P,

即式(26)成立.

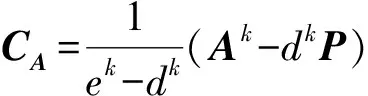
即式(27)成立； 當d≠e且dk=ek時, 由式(25)知(Ak-dkP)2=0, 此時式(27)成立.當d=e時, 由式(26)得

A2k=2kd2k-1A-(2k-1)d2kP=2dk[kdk-1A-(k-1)dkP]-d2kP=2dkAk-d2kP,

即(Ak-dkP)2=0, 此時式(27)成立.證畢.

推論1設P∈Ψn,A∈Ωn(P;d,e),k∈+, 則式(6)中的

αk=dk+dk-1e+…+dek-1+ek,βk=-(dke+dk-1e2+…+dek).

(28)

證明: 當d≠e時, 由式(25)和引理1知

再由式(6)知式(28)成立.當d=e時, 由

dk+dk-1e+…+dek-1+ek=(k+1)dk=αk, -(dke+dk-1e2+…+dek)=-kdk+1=βk,

并結合式(26)知式(28)成立.證畢.

定理2設P∈Ψn,A∈Ωn(P;d,e),f(x)∈[x],f′(x)為f(x)的導數, 則廣義多項式fP(A)滿足fP(A)P=PfP(A)=fP(A), 并且當d≠e時,

fP(A)=(f(e)-f(d))CA+f(d)P；

(29)

當d=e時,

fP(A)=f′(d)A+(f(d)-f′(d)d)P；

(30)

fP(A)∈Ωn(P;f(d),f(e)).

(31)

證明: 如式(7), 設f(x)=amxm+…+a1x+a0∈[x], 由式(19)和AP=PA=A得fP(A)P=PfP(A)=fP(A).當d≠e時, 由式(7),(11),(25)得

即式(29)成立.

當d=e時, 由式(7),(26)得

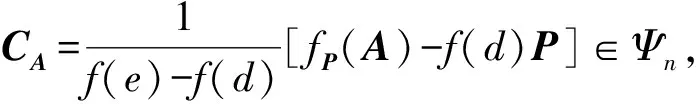
又當d=e時, 由A2=2dA-d2P及命題1和式(30), 得

即(fP(A)-f(d)P)2=0, 再由式(3)得式(31).證畢.

當A∈Ωn(I;dA,eA)時, 由定理2可得二次矩陣多項式的相應結論.

3 主要結果

定理3設P,Q∈Ψn,A∈Ωn(P;dA,eA),B∈Ωn(Q;dB,eB), 其中dAdBeAeB≠0,f(x),g(x)∈[x]滿足f(dA)f(eA)g(dB)g(eB)≠0.如果P-Q可逆, 則fP(A)-gQ(B)可逆.特別地, 當a,b∈且ab≠0,k,t∈+時,aAk+bBt可逆.

證明: 由定理2和式(31)知,

fP(A)∈Ωn(P;f(dA),f(eA)),gQ(B)∈Ωn(Q;g(dB),g(eB)).

再由f(dA)f(eA)g(dB)g(eB)≠0和式(2),(4),(5)得

因此由引理3可知fP(A)-gQ(B)可逆.

設f(1)(x)=axk,g(1)(x)=-bxt∈[x], 由dAdBeAeB≠0知,

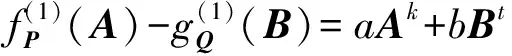
定理3表明,fP(A)-gQ(B)可逆只需滿足f(dA)f(eA)g(dB)g(eB)≠0, 而與多項式f(x),g(x)的選擇無關.當f(x)=g(x)=x時, 由定理3可得引理3.

定理4設P∈Ψn,A∈Ωn(P;dA,eA),B∈Ωn(P;dB,eB),f(x),g(x)∈[x].如果式(20)中ωωf,g≠0, 則廣義多項式fP(A),gP(B)的換位子滿足

r(fP(A)gP(B)-gP(B)fP(A))=r(AB-BA).

證明: 由式(11),(20),(25),(27)知,

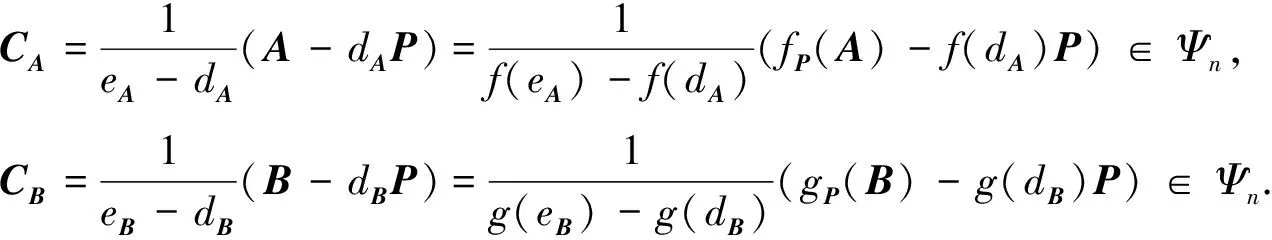
(32)

再由式(20),(32)得

即

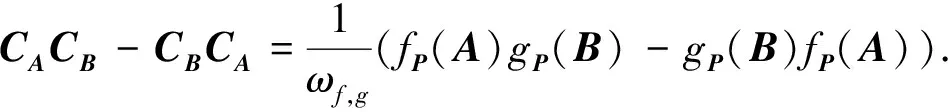
(33)

結合引理4中式(22)可知定理4的結論成立.證畢.

定理4表明, 在約束ωωf,g≠0下, 由同一個冪等矩陣確定的兩個廣義二次矩陣的兩個廣義多項式換位子的秩與多項式選擇無關.

推論2設P∈Ψn,A∈Ωn(P;dA,eA),B∈Ωn(P;dB,eB),f(x),g(x)∈[x].如果式(20)中ωωf,g≠0, 則廣義多項式fP(A),gP(B)的換位子滿足

且當dA=dB=d,eA=eB=e時, 有

當dA=1,eA=0時, 有

r(fP(A)gP(B)-gP(B)fP(A))=r(AB-BA)=r(ABA-AB)+r(ABA-BA);

(36)

當dA=dB=d=-eA=-eB≠0時, 有

r(fP(A)gP(B)-gP(B)fP(A))=r(AB-BA)=r(A-B)+r(A+B)-r(P).

(37)

證明: 當f(x)=g(x)=x時, 由定理4和引理4中式(21)知式(34)成立.再由式(34)分別可得式(35),(36).最后由式(35)知式(37)成立.證畢.

當f(x)=g(x)=x且dA=dB,eA=eB時, 由式(35)可得文獻[11]中的式(23).當P=I,f(x)=g(x)=x且取d=1,e=0(d=1,e=-1)時, 由式(35)(或(37))可得文獻[27](或文獻[28])給出的冪等(或對合)矩陣的秩等式(9)(或(10)).由式(36)可得文獻[11]的結論(式(24)), 表明秩等式(9)也適用于冪等矩陣和廣義二次矩陣； 式(37)表明式(10)也適用于數量對合矩陣[29].

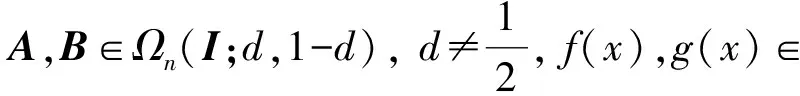
r(f(A)g(B)-g(B)f(A))=r(AB-BA)=r(A-B)+r(I-A-B)-n.

(38)