基于室內供暖溫度調控的數學建模研究
王嗣淇 鄧睿翔 顏志雄 佟東霖
(1、南京信息工程大學 人工智能學院,江蘇 南京 210044 2、南京信息工程大學 自動化學院,江蘇 南京 210044 3、南京信息工程大學 大氣科學學院,江蘇 南京 210044)
1 概述
供暖問題一向被許多人所關注,尤其在某些特殊領域,如醫療行業對室內溫度有嚴格要求。水暖是最流行的一種采暖方式,且在我國北方地區使用非常普遍,針對這種供暖方式,在外界溫度不斷變化的情況下,如何依靠控制進出水流量來控制室內溫度保持在一個合適的位置是一個具有實際意義的問題。由于封閉式內溫度場的測量點不計其數,目前多數的計算方式或是是采用具有代表意義的一個或幾個點代入計算,或是將三維空間轉化為二維求解[1],有或是建立三維熱傳導方程對空間動態溫度進行求解[2],前者可能會因為使用不穩定的數據而對整個溫度場的計算造成影響,第二者則會因維度較低而對空間溫度分布計算不準確,后者又會因維度較高計算復雜。故本文將南北墻面視作面熱源進行計算,減少了選取特征點帶來的誤差,并將整個三維空間節點化,進一步降低了計算難度。
2 模型建立
2.1 問題重述
冬季供暖采取熱水供熱方式的每一戶中有一個進水口和出水口,可以通過控制水流量來使室內溫度維持在一個相對穩定的范圍內。該房間參數如圖1。
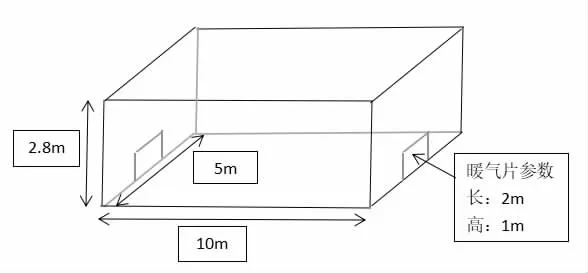
圖1 房間簡單示意圖
本文研究問題可描述為:(1)已知室外溫度為0℃,進水口流量為0.5m3/h,求房間的空間溫度分布。(2)當進水口流量在0.1m3/h-1.0m3/h 范圍內變化,求房間的動態溫度分布。(3)根據一天之內室外溫度變化情況每一小時調整一次進水口量,在保證室內溫度達標的情況下合理調整進水口流量,并使得一天累計耗水量最小。
2.2 問題假設
(1)進水口流量和外界溫度發生變化時,室內溫度達到穩態的時間很短。(2)房間與室外的熱交換只發生在最外圍的熱源節點。(3)內墻散失的熱量忽略不計。
2.3 空間節點溫度分布模型
2.3.1 散失熱量的求解。由于磚面和玻璃的材質和厚度不同,所以兩者傳熱系數也不同,整個墻面(包括窗戶)散失的熱量需要分開求解。查詢材料導熱系數總表可得,墻面磚塊部分導熱系數λ1為1.0W/(m·k),窗戶玻璃的導熱系數λ2為0.78W/(m·k)。根據常見房屋相關參數,假設墻面磚塊部分厚度σ1為30cm,窗戶玻璃的厚度σ2為0.4cm。
墻面磚塊與窗戶部分的傳熱系數Ki為:

公式(2)中負號表示散失,K 為傳熱系數,由于墻面磚塊部分和窗戶部分傳熱系數不同,兩個部分所占面積也不同,整體墻面的傳熱系數K 定義為不同材質部分與其面積的加權值。
2.3.2 產熱量的求解。暖氣片向房間散熱,相當于一個散熱器。暖氣片熱量來源于熱水,所以產生的總熱量與進、出水的溫度、進水口的流量和進水總量有關。在t1到t2的時間內,進水口的流量為G,進水溫度為uin,出水溫度為uout,產生的總熱量為:

其Δu 為溫度在x,y,z 三個方向上的二階導數之和。
2.3.4 空間節點模型
為求解空間溫度分布,本文將三維空間節點化,將房間劃分為51×101×29 的節點集,即把房間劃分為50×100×28 個小立方體區域,一個單位長度對應0.1m,網格的交點為節點,每一個節點都控制本身與周圍六個節點所占有空間,將這個空間稱為控制體,如圖2 所示。

圖2 節點與其控制體
我們將所有節點分為熱源節點與非熱源節點,熱源節點位于空間的邊界,他們的溫度只與自身前一刻的溫度決定,而非熱源節點的溫度受初始環境溫度與熱源節點的控制,由雅可比迭代法求解,對每一個節點分析,根據熱量守恒定律和傅里葉導熱定律,流入的熱量Qin與流出熱量Qout之差為該點熱量的增量Qst,其關系式如下:

2.4 動態流量模型
模型二在模型一的基礎上使進水口流量在0.1-1m3/h 之間變化,而由(4)式可知暖氣片產生的總熱量Q3與進水口流量直接相關,為了滿足基本供暖需求,其出水溫度也會發生變化。用傳熱系數、散熱器相關修正系數[3]和室內溫度表示暖氣片產生的總熱量與(3)式聯立可得如下表達式:

式中β1散為熱器組裝片數修正系數;β2散熱器連接形式修正系數;β3為散熱器安裝形式修正系數。
2.5 最小耗水量模型
問題三要求每隔一小時調整一次進水口流量,在保證室內日均溫度達到21℃且標準差為1.5 攝氏度的條件下,使得一天累計耗水量最小。設Gi(i=1,2,…,24)表示第i 小時內的進水口流量,ui(i=1,2,…,24)表示第i 時的平衡溫度。
進水量與屋外溫度和室內溫度存在函數關系:

3 結果分析
3.1 房間溫度分布
利用MATLAB 軟件畫出高度為0m、0.5m、1.0m、1.5m、2.0m 和2.8m 的溫度空間分布圖。其中選取具有代表性的兩個高度0m、和3m 的分布圖進行具體分析,如圖3 所示。
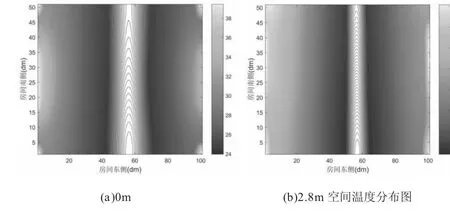
圖3
由圖3 可知,從南北方向來看,每個高度的分布圖都呈現靠近南、北墻兩端溫度相對較高、中間溫度相對較低的分布;而從東西方向來看,通過觀察等溫線可知,每個高度的分布圖都呈現中間溫度相對較高、兩端溫度相對較低的分布。這是因為距離熱源越遠的地方,所獲的熱量越低。另外,每個高度的分布圖四個角落處溫度都相對較低,這不僅與距離熱源的位置有關,也與外墻與外界的熱量交換有關。
再比較0m 和2.8m 的溫度分布圖,發現高度為2.8m所在平面中間低溫帶最窄且等溫線最密集,說明熱量在房間高處更易傳導,這與室內空氣流動快慢有一定關系。
3.2 流量變化時的動態溫度
針對問題二進水口的流量以0.1m3/h 等間隔依次利用雅克比迭代算法,其中進水溫度為40℃,出水溫度根據(13)式求得。利用MATLAB 求解得到進水口流量依次增加0.1m3/h 后房間的平均氣溫如表1 所示。
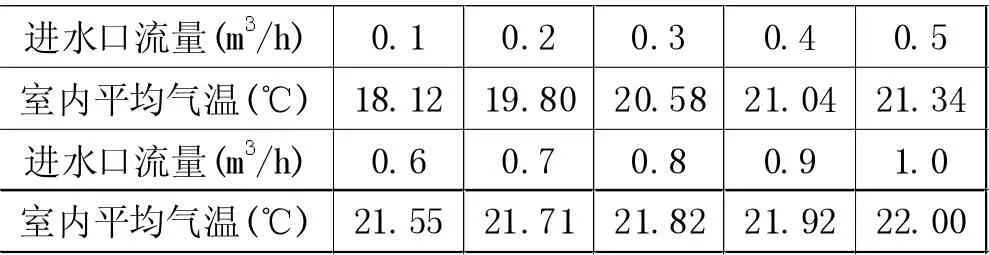
表1 進水口流量所對應的平均氣溫表
取x 為2.5m,z 為1.4m,溫度在y 軸方向(南北方向)變化曲線如圖4 所示。
由表1 和圖4 可知,房間的平均溫度與進水口流量呈現正相關,而進水口流量從0.1m3/h 增加到0.2m3/h 時溫度提高的幅度最大,然后進水口流量每增加0.1m3/h 溫度提高的幅度逐漸變小。所以在滿足室內正常溫度的情況下,進水口流量繼續增大對溫度提升的效果不明顯,且會造成耗水量的浪費。
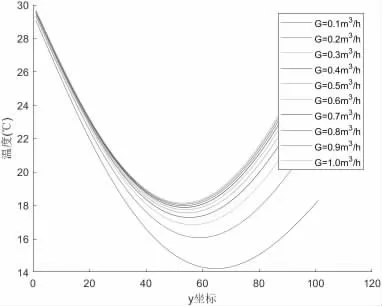
圖4 溫度在南北方向變化曲線
3.3 最小耗水量
利用lingo 軟件求解得到最小累計進水量為13.59m3,每個小時具體的進水口流量如表2 所示。

表2 每個小時的進水口流量(單位:m3/h)
4 結論
本文所研究熱水供暖的模型的目的是為了更好調整房間供暖系統的參數,并對系統的能源利用和溫度分布進行優化,即動態選取最佳的水流量與合適的暖氣片參數及位置來達到達到滿足用戶需求并節約能源的目的,滿足可持續發展的要求,因此這類問題的研究具有一定的實際應用價值。

