“四大理念”下的教學(xué)構(gòu)建

宋璨

[摘 要]“四大理念”是指設(shè)定大目標(biāo)，凝練大概念，用好大問題，形成大結(jié)構(gòu)。構(gòu)建“四大理念”下的教學(xué)，實(shí)施深度教學(xué)，可以培養(yǎng)學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)，樹立學(xué)生的數(shù)學(xué)觀念和數(shù)學(xué)研究意識。

[關(guān)鍵詞]四大理念;教學(xué)構(gòu)建;四點(diǎn)共圓

[中圖分類號]? ? G633.6? ? ? ? [文獻(xiàn)標(biāo)識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2022）11-0019-03

江蘇省特級教師王為峰提出了“四大理念”，即設(shè)定大目標(biāo)，凝練大概念，用好大問題，形成大結(jié)構(gòu)。“四大理念”強(qiáng)調(diào)的是培養(yǎng)學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)，樹立學(xué)生的數(shù)學(xué)觀念和數(shù)學(xué)研究意識。所謂大目標(biāo)，就是對最大限度地發(fā)揮學(xué)科教學(xué)育人功能的預(yù)期，或者說是對學(xué)生學(xué)習(xí)取得最大成果的預(yù)期。凝練大概念，用好大問題，形成大結(jié)構(gòu)是實(shí)現(xiàn)大目標(biāo)的手段和過程。筆者曾有幸開設(shè)了一節(jié)區(qū)公開課，嘗試在“四大理念”下進(jìn)行教學(xué)構(gòu)建，現(xiàn)在整理成文，與大家交流。

一、教學(xué)內(nèi)容及解析

（一）教學(xué)內(nèi)容

四點(diǎn)共圓的條件的探究和證明。

（二）內(nèi)容解析

四點(diǎn)共圓的條件是在學(xué)習(xí)了過一個點(diǎn)的圓、過兩個點(diǎn)的圓、過不在同一條直線上的三個點(diǎn)的圓、三角形與圓的關(guān)系、圓的內(nèi)接四邊形后，對經(jīng)過任意三點(diǎn)都不在同一條直線上的四點(diǎn)共圓的條件的探究。在學(xué)過“圓內(nèi)接四邊形的對角互補(bǔ)”后，相應(yīng)地，會產(chǎn)生這樣的疑問：對角互補(bǔ)的四邊形的四個頂點(diǎn)共圓嗎？ 探究四點(diǎn)共圓的條件是促進(jìn)學(xué)生思維自然生長的需要，也是進(jìn)一步在數(shù)學(xué)活動中培養(yǎng)學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)的需要。

在四點(diǎn)共圓條件的探究過程中，通過對特殊四邊形（平行四邊形、矩形、等腰梯形、共斜邊的兩個直角三角形等）的探究，發(fā)現(xiàn)一般規(guī)律（過對角互補(bǔ)的四邊形的四個頂點(diǎn)能作一個圓），體現(xiàn)了由特殊到一般的思想。同時，從三點(diǎn)共圓入手探究四點(diǎn)共圓的條件，以及把四點(diǎn)共圓的證明轉(zhuǎn)化為點(diǎn)與圓的位置關(guān)系的證明，都體現(xiàn)了轉(zhuǎn)化的思想。學(xué)生經(jīng)歷探究四點(diǎn)共圓的條件這一數(shù)學(xué)活動的全過程，在“做”和“思考”的過程中有效積累了數(shù)學(xué)活動經(jīng)驗(yàn)和形成了幾何直觀。

基于以上分析，確定本節(jié)課的教學(xué)重點(diǎn)是四點(diǎn)共圓條件的探究。

二、教學(xué)目標(biāo)及解析

（一）教學(xué)目標(biāo)

（1）理解過某個四邊形的四個頂點(diǎn)能作一個圓的條件;

（2）通過四點(diǎn)共圓條件的探究和猜想的證明，體會由特殊到一般、轉(zhuǎn)化等數(shù)學(xué)思想，積累數(shù)學(xué)活動經(jīng)驗(yàn)，發(fā)展幾何直觀能力。

（二）目標(biāo)解析

實(shí)現(xiàn)目標(biāo)（1）的標(biāo)志：能通過畫圖操作，發(fā)現(xiàn)一般規(guī)律：過對角互補(bǔ)的四邊形的四個頂點(diǎn)能作一個圓，并能證明結(jié)論的正確性。

實(shí)現(xiàn)目標(biāo)（2）的標(biāo)志：能從三點(diǎn)共圓入手探究四點(diǎn)共圓的條件，并能通過對特殊四邊形的探究，發(fā)現(xiàn)一般規(guī)律：過對角互補(bǔ)的四邊形的四個頂點(diǎn)能作一個圓。在證明猜想的過程中，能將四點(diǎn)共圓的問題轉(zhuǎn)化為點(diǎn)與圓的位置關(guān)系去研究。

三、教學(xué)問題分析

對于四點(diǎn)共圓條件的證明，需要將四點(diǎn)共圓的問題轉(zhuǎn)化為點(diǎn)與圓的位置關(guān)系的問題，即第四個點(diǎn)在不在前三個點(diǎn)確定的圓上，再利用反證法去證明。學(xué)生雖然學(xué)過反證法，但應(yīng)用較少，所以在證明時會存在一些困難。

本節(jié)課的教學(xué)難點(diǎn)是對角互補(bǔ)的四邊形的四個頂點(diǎn)共圓的證明。

四、教學(xué)過程

活動一： 想一想。

問題1.過一點(diǎn)能作幾個圓？

問題2.過兩個點(diǎn)能作幾個圓？

問題3.過三個點(diǎn)呢？

問題4.接下來，你會提出什么問題？

設(shè)計(jì)意圖：從學(xué)生已有的知識經(jīng)驗(yàn)出發(fā)，提出問題，同時滲透將探究四點(diǎn)共圓問題轉(zhuǎn)化成三點(diǎn)共圓的問題，也就是第四個點(diǎn)在不在前三個點(diǎn)已經(jīng)確定的圓上的問題，為后續(xù)猜想的證明做好鋪墊。

活動二：畫一畫。

問題1. 經(jīng)過什么樣的四個點(diǎn)可以作出一個圓，也就是過什么樣的四邊形的四個頂點(diǎn)可以作出一個圓？你準(zhǔn)備用什么想法或者思路去解決這個問題？

問題2. 你覺得過什么樣的四邊形的四個頂點(diǎn)能作出一個圓呢？分組畫一畫，試一試。

問題3. 從小組長展示的研究成果中，你有什么發(fā)現(xiàn)？

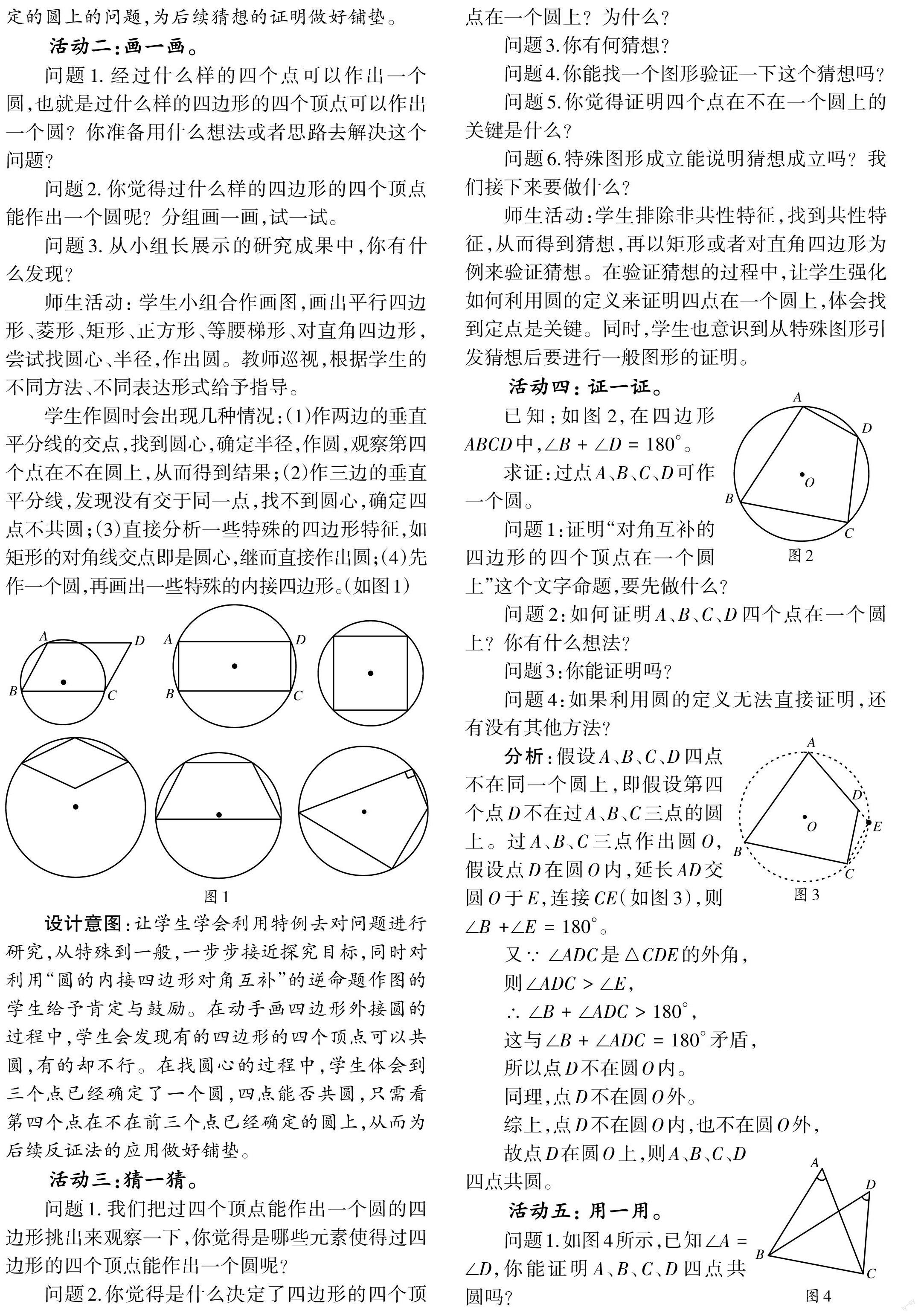
師生活動： 學(xué)生小組合作畫圖，畫出平行四邊形、菱形、矩形、正方形、等腰梯形、對直角四邊形，嘗試找圓心、半徑，作出圓。教師巡視，根據(jù)學(xué)生的不同方法、不同表達(dá)形式給予指導(dǎo)。

學(xué)生作圓時會出現(xiàn)幾種情況：（1）作兩邊的垂直平分線的交點(diǎn)，找到圓心，確定半徑，作圓，觀察第四個點(diǎn)在不在圓上，從而得到結(jié)果;（2）作三邊的垂直平分線，發(fā)現(xiàn)沒有交于同一點(diǎn)，找不到圓心，確定四點(diǎn)不共圓;（3）直接分析一些特殊的四邊形特征，如矩形的對角線交點(diǎn)即是圓心，繼而直接作出圓;（4）先作一個圓，再畫出一些特殊的內(nèi)接四邊形。（如圖1）

設(shè)計(jì)意圖：讓學(xué)生學(xué)會利用特例去對問題進(jìn)行研究，從特殊到一般，一步步接近探究目標(biāo)，同時對利用“圓的內(nèi)接四邊形對角互補(bǔ)”的逆命題作圖的學(xué)生給予肯定與鼓勵。在動手畫四邊形外接圓的過程中，學(xué)生會發(fā)現(xiàn)有的四邊形的四個頂點(diǎn)可以共圓，有的卻不行。在找圓心的過程中，學(xué)生體會到三個點(diǎn)已經(jīng)確定了一個圓，四點(diǎn)能否共圓，只需看第四個點(diǎn)在不在前三個點(diǎn)已經(jīng)確定的圓上，從而為后續(xù)反證法的應(yīng)用做好鋪墊。

活動三：猜一猜。

問題1. 我們把過四個頂點(diǎn)能作出一個圓的四邊形挑出來觀察一下，你覺得是哪些元素使得過四邊形的四個頂點(diǎn)能作出一個圓呢？

問題2.你覺得是什么決定了四邊形的四個頂點(diǎn)在一個圓上？為什么？

問題3.你有何猜想？

問題4.你能找一個圖形驗(yàn)證一下這個猜想嗎？

問題5.你覺得證明四個點(diǎn)在不在一個圓上的關(guān)鍵是什么？

問題6.特殊圖形成立能說明猜想成立嗎？我們接下來要做什么？

師生活動：學(xué)生排除非共性特征，找到共性特征，從而得到猜想，再以矩形或者對直角四邊形為例來驗(yàn)證猜想。在驗(yàn)證猜想的過程中，讓學(xué)生強(qiáng)化如何利用圓的定義來證明四點(diǎn)在一個圓上，體會找到定點(diǎn)是關(guān)鍵。同時，學(xué)生也意識到從特殊圖形引發(fā)猜想后要進(jìn)行一般圖形的證明。

活動四： 證一證。

已知：如圖2，在四邊形[ABCD]中，[∠B+∠D=180°]?

求證：過點(diǎn)[A]、[B]、[C]、[D]可作一個圓。

問題1：證明“對角互補(bǔ)的四邊形的四個頂點(diǎn)在一個圓上”這個文字命題，要先做什么？

問題2：如何證明[A]、[B]、[C]、[D]四個點(diǎn)在一個圓上？你有什么想法？

問題3：你能證明嗎？

問題4：如果利用圓的定義無法直接證明，還有沒有其他方法？

分析：假設(shè)[A]、[B]、[C]、[D]四點(diǎn)不在同一個圓上，即假設(shè)第四個點(diǎn)[D]不在過[A]、[B]、[C]三點(diǎn)的圓上。過[A]、[B]、[C]三點(diǎn)作出圓[O]，假設(shè)點(diǎn)[D]在圓[O]內(nèi)，延長[AD]交圓[O]于[E]，連接[CE]（如圖3），則[∠B +∠E =180°]。

又∵ [∠ADC]是[△CDE]的外角，

則[∠ADC>∠E]，

∴ [∠B+∠ADC>180°]，

這與[∠B+∠ADC =180°]矛盾，

所以點(diǎn)[D]不在圓[O]內(nèi)。

同理，點(diǎn)[D]不在圓[O]外。

綜上，點(diǎn)[D]不在圓[O]內(nèi)，也不在圓[O]外，

故點(diǎn)[D]在圓[O]上，則[A]、[B]、[C]、[D]四點(diǎn)共圓。

活動五： 用一用。

問題1.如圖4所示，已知[∠A=∠D]，你能證明[A]、[B]、[C]、[D]四點(diǎn)共圓嗎？

問題2. 你能用結(jié)論“對角互補(bǔ)的四邊形四點(diǎn)共圓”來證明嗎？

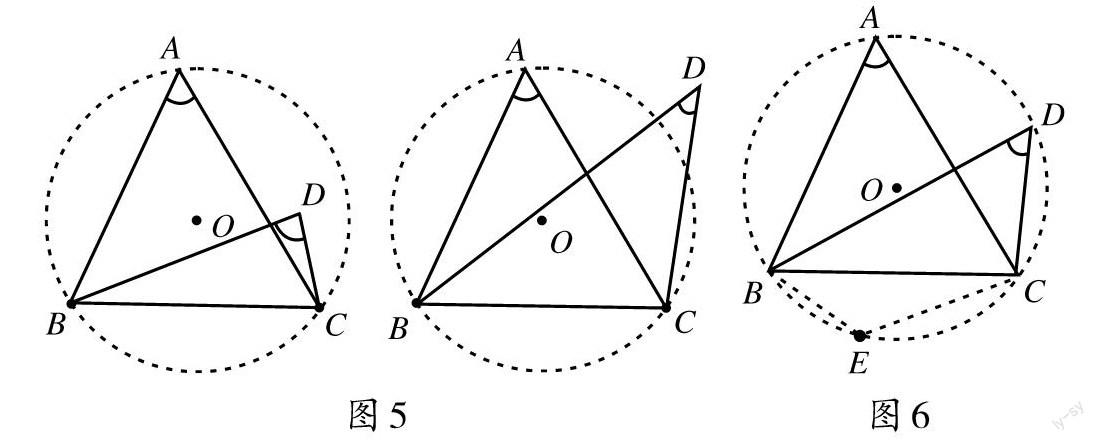
方法一：反證法。

分析：過[A]、[B]、[C]三點(diǎn)作出圓[O]，分別假設(shè)點(diǎn)[D]在圓[O]內(nèi)或圓[O]外（如圖5），推出矛盾，從而假設(shè)不成立，點(diǎn)[D]在圓[O]上。

方法二：利用“對角互補(bǔ)的四邊形的四個頂點(diǎn)共圓”來證明。

證明：如圖6，過[A]、[B]、[C]三點(diǎn)作出圓[O]，在圓[O]上取點(diǎn)[E]，連接[BE]、[CE]。

∵點(diǎn)[A]、[B]、[E]、[C]在圓[O]上，

∴[∠A+∠E=180°]，

又∵ [∠A=∠D]，

∴[∠D+∠E=180°]。

∴點(diǎn)[D]、[B]、[E]、[C]四點(diǎn)共圓，

即點(diǎn)[D]也在圓[O]上，

∴[A]、[B]、[C]、[D]四點(diǎn)共圓。

五、教學(xué)思考

（一）重視活動經(jīng)驗(yàn)積累，培養(yǎng)數(shù)學(xué)核心素養(yǎng)

蘇科版教材中并沒有“探究四點(diǎn)共圓的條件”這一課， 但是在學(xué)習(xí)“不在同一條直線上的三點(diǎn)確定一個圓” 后，學(xué)生積累了豐富的數(shù)學(xué)活動經(jīng)驗(yàn)。

（1）構(gòu)建了經(jīng)過已知點(diǎn)作圓的探索思路，從“經(jīng)過一個點(diǎn)作圓”“經(jīng)過兩個點(diǎn)作圓”到“經(jīng)過三個點(diǎn)作圓”，逐漸增加點(diǎn)的個數(shù)，分別進(jìn)行探究;

（2）明確了作圓需要圓心和半徑，從而確定圓的位置和大小;

（3）“經(jīng)過三個點(diǎn)作圓”需要建立在“三點(diǎn)不在同一條直線上”的前提條件下，這在一定程度上體現(xiàn)了分類討論思想;

（4）具有一定的邏輯推理能力，針對“經(jīng)過同一條直線上的三個點(diǎn)不能作出一個圓”，能應(yīng)用反證法進(jìn)行證明。

積累這些數(shù)學(xué)活動經(jīng)驗(yàn)后，有的學(xué)生自然而然地思考有關(guān)四點(diǎn)共圓條件的問題，尤其是在學(xué)習(xí)“圓內(nèi)接四邊形的對角互補(bǔ)”后，有的學(xué)生開始產(chǎn)生疑問：對角互補(bǔ)的四邊形的四個頂點(diǎn)是否也是共圓的呢？選擇此課題，是學(xué)生思維自然生長的需要，有利于培養(yǎng)學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)。

（二）通過數(shù)學(xué)探究，關(guān)注數(shù)學(xué)素養(yǎng)形成

本節(jié)課通過五個教學(xué)環(huán)節(jié)的設(shè)計(jì)，生成的不僅是四點(diǎn)共圓的條件，而且讓學(xué)生體會到了研究圖形的性質(zhì)就是研究其構(gòu)成要素或其相關(guān)要素之間所具有的位置關(guān)系或數(shù)量關(guān)系。還有從特殊到一般的研究問題思路，將未知問題轉(zhuǎn)化為已知問題的研究方法，運(yùn)用“觀察—猜想—證明”得到一些新的數(shù)學(xué)結(jié)論的過程，這些方面對學(xué)生創(chuàng)新意識的培養(yǎng)和推理能力的提升都有非常重要的作用。

（三）問題是思維的源泉，更是思維的動力

當(dāng)圍繞大目標(biāo)提煉出大概念后，就可以在大概念的引領(lǐng)下提出大問題。大問題可以從兩個方面去認(rèn)識，一是按照問題從大到小的順序進(jìn)行啟發(fā)提問，二是提出能夠觸及數(shù)學(xué)本質(zhì)的問題。如本節(jié)課先后提四個主要問題：通過四邊形四個頂點(diǎn)作圓的結(jié)果如何？如何判斷這四個點(diǎn)共圓或不共圓？如何證明你的猜想？你能用所學(xué)知識判斷四個點(diǎn)在圓上嗎？

（四）基于認(rèn)知沖突與問題解決，設(shè)計(jì)學(xué)生活動

本節(jié)課的研究內(nèi)容既是“過三點(diǎn)的圓”的延續(xù)和拓展，又是“圓內(nèi)接四邊形性質(zhì)”的逆向思維的發(fā)展。本節(jié)課設(shè)計(jì)了“想一想”“畫一畫”“猜一猜”“證一證”“用一用”等活動，喚醒學(xué)生已有的知識經(jīng)驗(yàn)，引導(dǎo)學(xué)生構(gòu)建探究的基本思路，讓學(xué)生體驗(yàn)數(shù)學(xué)發(fā)現(xiàn)的一般過程，感悟數(shù)學(xué)思想方法的獨(dú)特精妙，發(fā)展學(xué)生應(yīng)用與創(chuàng)新的學(xué)科素養(yǎng)。

（五）“四大理念”下的教學(xué)改進(jìn)

（1）畫一畫。從提供部分特殊圖形到不提供任何圖形，讓學(xué)生完全自主作圖。

（2）猜一猜。從有人答出一種猜想即可到鼓勵學(xué)生思維多元化，引導(dǎo)學(xué)生從特殊圖形、逆命題等多角度提出猜想。

（3）想一想。在證明四點(diǎn)共圓的條件時，學(xué)生會基于已有知識經(jīng)驗(yàn)，選擇用圓的定義去證明。教學(xué)設(shè)計(jì)從起初給學(xué)生搭梯子，提示用反證法，改為不做提示，讓學(xué)生的思維自然生長。

[? ?參? ?考? ?文? ?獻(xiàn)? ?]

[1]? 中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)：2011年版[M].北京：北京師范大學(xué)出版社，2012.

[2]? 徐玉慶.初中數(shù)學(xué)教科書中數(shù)學(xué)探究活動的分析：以人教版數(shù)學(xué)教材為例[J].中學(xué)數(shù)學(xué)，2016（2）：35-37.

[3]? 曹廣福，張蜀青.問題驅(qū)動的中學(xué)數(shù)學(xué)課堂教學(xué)[M].北京：清華大學(xué)出版社，2018.

（責(zé)任編輯 黃桂堅(jiān)）