既有拱橋光彩亮化改造后吊索的渦振性能

唐浩俊 鄧周全 王澤文 李永樂

摘 要：為確定既有拱橋亮化改造后柔性吊索的渦激共振性能，結合數值模擬和風洞試驗 開展了研究.針對既有吊索和新增吊索的亮化方案，對典型斷面在不同來流風向下的繞流特 性進行了模擬，并討論了氣動力系數和旋渦脫落行為隨風向角的演變規律.然后，通過節段模型風洞試驗測試了吊索在不同風向角來流作用下的渦振響應，并結合數值模擬的結果對試驗 現象進行了分析.結果表明：在既有吊索上安裝亮化燈具顯著改變了其渦振性能.當來流風垂直于橋軸線時，沿索軸方向兩種典型截面的旋渦脫落頻率、強度有較大差異，減小了吊索整體發生渦激共振的可能;當來流風向角在30°附近時，兩種典型截面的旋渦脫落特性趨于一致，增大了吊索整體發生渦激共振的可能.新增吊索更為輕柔，外包矩形燈罩后發生渦激共振的可能性很大，需要考慮必要的抑振措施.

關鍵詞：拱橋;吊索;光彩亮化;渦激共振;數值模擬;風洞試驗

中圖分類號：U448.22 文獻標志碼：A

Vortex-induced Vibration of Hangers Equipped

with Lighting Fixtures of Existing Arch Bridges

TANG Haojun1，2?，DENG Zhouquan1，WANG Zewen1，LI Yongle1，2 （1.Department of Bridge Engineering，Southwest Jiaotong University，Chengdu610031，China;

2.Wind Engineering Key Laboratory of Sichuan Province，Chengdu610031，China）

Abstract：In order to determine the vortex-induced vibration of the flexible hangers equipped with lighting fix-tures of an existing arch bridge，numerical simulations and wind tunnel tests were carried out.Aiming at the lighting schemes for the existing hanger and the additional hanger，the flow characteristics around typical cross-sections with different yaw angles were simulated.The variations laws of the aerodynamic coefficients and the vortex-shedding be-havior with the yaw angle are discussed.Then，the vortex-induced vibrations of hangers with different yaw angles were determined by segment wind tunnel tests.The experimental phenomena are discussed together with the results of the numerical simulations.The results show that the installation of lighting fixtures significantly changes the vortex-induced vibration performance of existing hangers.When the incoming flow is perpendicular to the bridge axis，the vortices shed from two typical cross-sections along the cable axis are different in frequency and intensity，which decreases the possibility of the vortex-induced vibration of hangers.When the yaw angle of the incoming flowis around30°，the vortex-shedding characteristics of the two typical sections tend to be consistent，which enhances the possibility of the vortex-induced vibration of hangers.The additional hangers，which are enclosed in rectangular lighting fixtures，show more flexible characteristics and are more likely to suffer from vortex-induced vibration，so additional countermeasures need to be considered.

Key words：arch bridge;hangers;lighting fixture;vortex-induced vibration;numerical simulations;wind tunnel tests

隨著城市建設不斷發展和人們精神文化需求日益增長，對既有建筑進行光彩亮化改造已成為一種趨勢.大跨度橋梁是交通運輸的紐帶，亦是一道靚麗的風景線.在亮化改造的趨勢下，它們又被賦予了新的使命，綻放出新的光彩.拱橋和斜拉橋都具有優美的結構外形，通常是一座城市的代表性建筑，也常成為光彩亮化工程的點睛之筆.

景觀設計人員更加關心如何提高光彩照明效果，而科研人員則需要關心如何確保結構的抗風安全.李壽英與陳政清[1]研究了某斜拉橋的斜拉索安裝亮化燈具后的馳振可能性，發現馳振的原因和兩根平行于索軸線、直徑12mm的鋼絲有關.董國朝等[2]提出了一種流固耦合分析方法用以模擬和分析 風致振動現象，在機理上解釋了安裝亮化燈具后馳 振力的形成過程.徐升橋與劉永鋒[3]介紹了京新上 地斜拉橋的亮化方案，為了提高斜拉索的抗風性能，將亮化燈具嵌入了斜拉索的護套內.周傲秋等[4]指 出燈具的存在導致斜拉索有較大概率發生馳振，而 去掉燈具直接安裝 LED點光源則可以降低斜拉索發生馳振的概率.鄧周全等[5]通過風洞試驗發現安裝 燈具后斜拉索的渦激共振現象有較大變化，其鎖定 風速會出現降低，并在較大的風向范圍內具備馳振的可能性[6].由此可見，亮化燈具的安裝改變了索截 面的氣動外形，對索結構的抗風性能產生了很大的影響.相比氣候條件變化對索截面氣動外形的影響，例如覆冰或風雨的影響，亮化燈具造成的影響更加明顯且持久.

亮化改造通常使用投光燈、泛光燈、點光源等.近年來，為了改善燈光效果，在拱橋的吊索或斜拉橋的斜拉索表面安裝集成了LED點光源的燈罩已成為主流趨勢.通常，索截面為圓形，而燈罩截面可近似 看作矩形，內部敷設電纜等設施.圓柱繞流和方柱繞 流都是經典的流體力學問題.但是，這兩種截面的旋 渦脫落特性卻有較大差異.

圓柱繞流的雷諾數效應非常突出，即使在高雷諾數下仍很明顯[7-9].圓形截面看似形狀簡單、規則，實則流場結構復雜、多變，涉及來流的分離、再附著、旋渦的形成等.矩形截面的流動分離點相對固定，流 場特征與自身的寬高比相關[10-12].可以預見，當這兩種氣動性能差異明顯的截面靠近或結合在一起時，圓截面對雷諾數的敏感性，以及矩形截面對來流風向和自身寬高比的敏感性，都將成為影響組合截面 流場結構的關鍵因素，使安裝了亮化燈具柔性索的氣動性能具有更多的不確定性.雖然前述提及的研究工作有助于我們掌握組合截面柔性索的風致振動行為，但目前的研究工作還非常有限，對組合截面氣動特性的認識也還遠不夠.

本文以某座中承式系桿拱橋的亮化方案為背 景.針對既有吊索的改造方案和新增吊索的設計方案，通過二維數值模擬對典型截面的旋渦脫落特性 進行了分析，開展了節段模型風洞試驗測試典型吊索的渦激共振響應，并據此對其余吊索的渦振性能進行了分析.研究結論可為相關的柔性索亮化工程設計和研究提供參考.

1? 工程背景

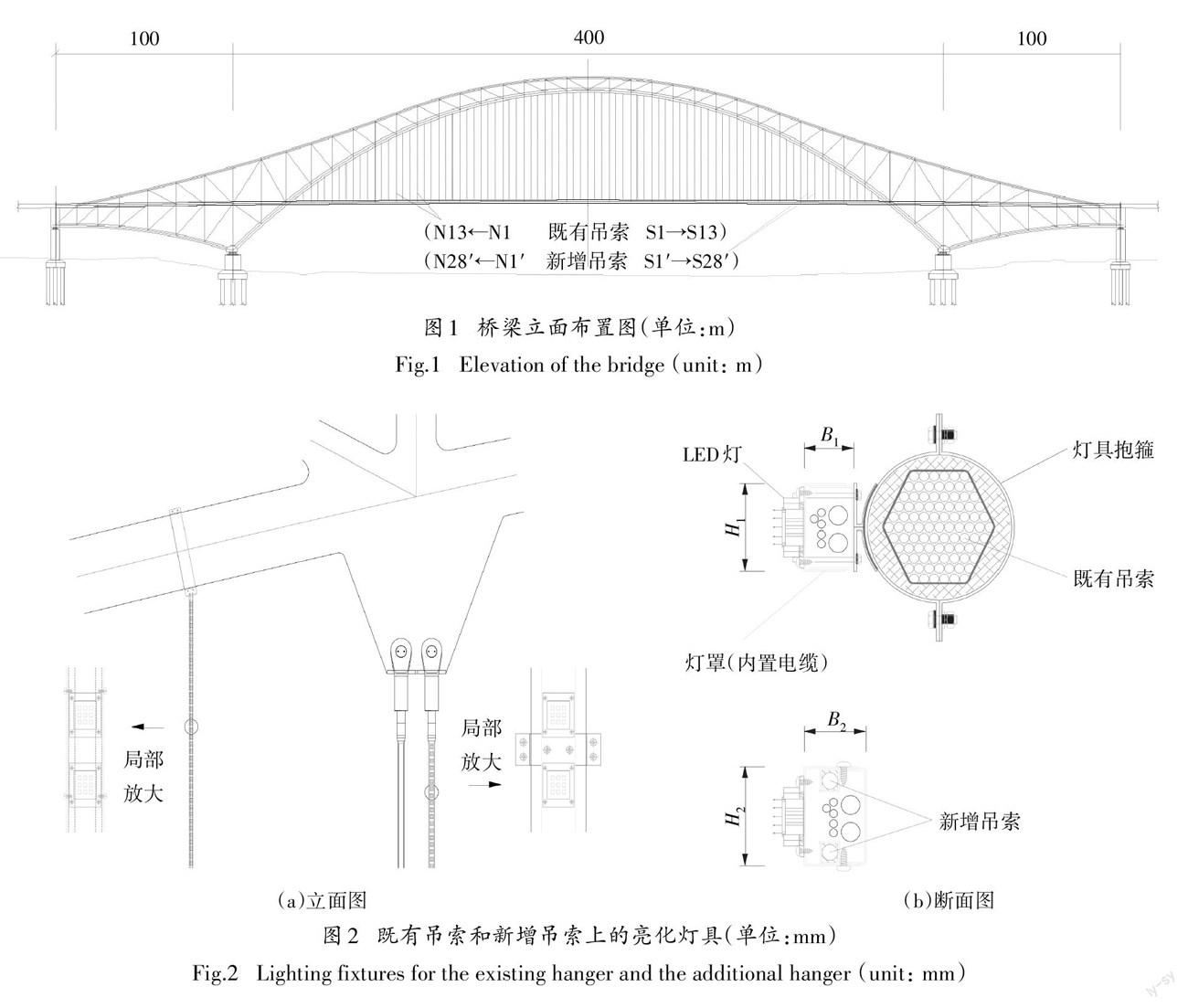
某座中承式拱橋全長600m，跨徑100m+400m+100m，拱頂至橋面69m，如圖1所示.全橋共 54個吊 點，相鄰吊點間距12m.各吊點處有兩根柔性吊索，吊索間距為0.54 m，彼此間無連接，亮化燈具僅安裝于其中一根吊索上.既有吊索內部采用標準強度為1670mPa的鍍鋅平行鋼絲，外部纏繞纖維增強聚酯 帶并設置緊貼的聚乙烯護套，直徑為97 mm.考慮其中一副吊索，跨中處的既有吊索編號為M，其南側吊索從跨中向端部依次編號為S1→ S13，其北側吊索從跨中向端部依次編號為N1→N13.為了達到更好的亮化效果，在既有吊索之間新增兩處吊索，如圖2所示，采用標準強度為1670mPa的鍍鋅平行鋼絲，鋼 絲直徑為11mm，兩支為一組.各組吊索從跨中向南、北兩側分別編號為S1′→ S28′、N1′→N28′.

亮化燈具由燈罩、LED 燈、電纜三個部分組成.其中，燈罩沿索軸向通長布置;LED 燈間隔111mm 嵌于燈罩表面，朝橋面外側凸出;電纜線置于鋁制燈 罩的內部為各 LED 燈供電.對于既有吊索，亮化燈具 通過間隔的抱箍附于其中一根上.燈罩順橋向寬度H1=59.6 mm，橫橋向寬度B1=34.4 mm，燈罩與吊索之 間存在約10mm的間隙.燈罩面積與吊索面積之比達到了27.7%，顯著改變了截面的氣動外形.對于新增吊索，亮化燈具包裹住兩根鋼絲.燈罩順橋向寬度H2=67.6 mm，橫橋向寬度B2=42.9mm.

2? 截面的旋渦脫落特性

2.1數值模型及無關性驗證

本節基于計算流體力學軟件 FLUENT，通過二 維計算模擬了吊索截面的繞流特性.如前所述，既有吊索和新增吊索上的亮化燈罩沿索軸方向通長布 置，但 LED 燈間隔嵌于燈罩表面并向外凸出.為了考慮局部 LED 燈對截面旋渦脫落特性造成的影響，分別建立了有燈罩及其上 LED 燈的計算截面和有燈罩 但不含其上 LED 燈的計算截面.圖3（a）給出了既有吊索計算截面的數值模型，同時包含同一吊點另一根不裝燈具的吊索，縮尺比為1∶1，以避免雷諾數的影響.計算區域為長方形，為減小壁面對圓柱繞流的干擾，上下邊界之間的距離略大于60D，對應的阻塞率約3.3%，圓截面中心距左側入口邊界18D，距右側 出口邊界 50D，其中D為吊索的直徑.圖3（b）給出了新增吊索計算截面的數值模型，同樣按1∶1縮尺比建立.上下邊界之間的距離約為50H2，對應的阻塞率約2%，燈罩中心距左側入口邊界 20B2，距右側出口 邊界 70B2，其中H2為燈罩順橋向寬度，B2為燈罩橫橋向寬度.

采用非定常計算，湍流模型為SST k-ω模型;用SIMPLEC算法解決動量方程中速度分量和壓力的耦 合問題;動量方程、湍動能方程及湍流耗散率方程均采用二階離散式.以無LED 燈的既有吊索截面和新增吊索截面為例進行時間步長無關性計算，取風向角為0°，計算風速為15m/s，采用不同的時間步長進行模擬，提取各截面的平均阻力系數CD-mean和均方根升力系數CL-RMS.對于既有吊索，將安裝了燈具的索截面標記為A，未安裝燈具的索截面標記為B;對于新增吊索，其截面標記為C.計算結果如表1所示，為了便于比較各個截面的氣動力系數，其特征尺寸均 取既有吊索的索徑.

對于這三個計算截面，當時間步長分別達到0.0005s、0.0001s、0.0001s 后，繼續減小時間步長對其氣動力系數的影響較小.為兼顧計算精度與效率，后續計算取時間步長為0.0001s.此時，索B（圓截 面）對應的雷諾數約為105，其阻力系數平均值為1.03，與多篇文獻[8，13-17]通過風洞試驗或數值模擬得到的結果范圍1.0～1.2相符.

基于該時間步長，進一步對網格數量無關性進行驗證.在前述計算中，兩個模型的網格數量分別為18.36 萬和14.90萬（標記為取定工況）.現通過調整 壁面網格寬度、厚度及增長率，將兩個模型的網格數量減少至14.10萬和11.63萬（標記為工況減1），再減 少至10.15 萬和8.21萬（標記為工況減 2）;增加至22.34 萬和18.51萬（標記為工況加1），如表2所示.可以看到，前述計算中網格數量足夠，繼續增加網格對結果幾乎沒有影響，而網格數量減少后計算結果出現了一定程度的變化.

2.2 外附矩形截面的旋渦脫落特性

既有吊索外附矩形燈罩后，其截面的氣動力系數發生了很大變化.表1中僅考慮了來流風垂直于橋軸線，即風向角為0°的情況.考慮到來流風向的不 確定性，進一步計算-30°～+30°風向角時截面的氣動力系數.同一吊點處兩根吊索中僅一根外附有矩形 燈罩，故正、負風向的結果不相同，定義負風向來流在順橋方向先流經有外附燈罩的吊索，正風向來流在順橋方向先流經無外附燈罩的吊索.以吊索圓心 作為氣動力的監控點，有外附燈罩吊索截面（以下簡稱組合截面）的平均阻力、升力系數如圖4所示.其中，氣動力為吊索與燈罩氣動力之和，特征尺寸取吊索直徑，坐標系選用體軸坐標系.組合截面升力系數均方根值如圖5所示，并對升力時程曲線進行了頻譜分析，根據其卓越頻率換算了對應的斯托羅哈數St.

由計算結果可以看到，燈罩上局部 LED 燈對組 合截面的平均氣動力系數產生了較大的影響.當風向角在0°附近時，有、無LED 燈的組合截面的平均氣動力系數相近.當風向角達到±4°時，兩組合截面的平均氣動力系數開始出現差異.隨著風向角的增大，兩者差異也逐漸增大，有LED 燈組合截面的平均阻力系數基本保持不變;而平均升力系數變化更明顯，其斜率大于無LED 燈組合截面.當風向角達到-18°、+16°時，有LED 燈組合截面的平均阻力系數開始增加，而平均升力系數基本不變.隨著風向角進一步增大，兩組合截面的平均氣動力系數趨于一致.

安裝燈罩后組合截面升力系數均方根值在較大的風向角范圍內明顯降低.0°風向角時，有LED 燈組 合截面的降幅更大，達到了89.4%;無LED 燈組合截 面的降幅要小些，也達到了39.6%.此外，LED 燈對截 面的旋渦脫落頻率影響顯著，達到了兩倍的差異，無LED 燈組合截面的St數明顯下降.

圖6給出了0°風向角時，組合截面升力達到最大（方向向上）及最小（方向向下）時流場的渦量云圖.由圖6可知，來流在燈罩兩側的倒角處發生分離 并在吊索表面再附著，這相當于增加了組合截面的順風向寬度.尾流區域內，旋渦被明顯拉長，脫落位置的后移使截面升力系數的波動減小.圖6中還標 出了組合截面尾流區域內的旋渦，從上、下側脫落的旋渦分別標注為“上”“下”，并按脫落先后標注編號.燈罩上有、無LED 燈兩種組合截面的旋渦脫落頻率不同，尾流中旋渦分布及發展規律也存在差異，降低了吊索發生渦激共振的可能性.

當風向角增大至+4°，或減小至-6°時，無LED 燈 組合截面的旋渦脫落頻率突然增大.隨著風向角絕對值進一步增大至10°～14°，有、無LED 燈組合截面的升力系數均方根值與斯托羅哈數均比較接近.隨后，兩組合截面的旋渦脫落特性再次出現差異，直到風向角絕對值接近30°時，它們的升力系數均方根值與斯托羅哈數再次接近.圖7給出了30°風向角時，組合截面升力達到最大及最小時流場的渦量云圖.可以看到，斜向來流風可穿過燈罩與吊索之間的空隙，弱化了LED 燈對流場結構的影響.此時，燈罩上有、無LED 燈兩種組合截面的旋渦脫落頻率相近（見圖5中的斯托羅哈數St），尾流中旋渦分布及發展規 律也更加同步，這增大了吊索結構發生渦激共振的可能性.

2.3 外包矩形截面的旋渦脫落特性

新增吊索外包燈罩后，其截面的氣動外形相當于矩形.考慮到來流風向的不確定性，計算了0° ～ +30°風向角時截面的氣動力系數，并考慮了有、無LED 燈的情況.由于計算區域內僅有一個截面，其氣動力系數的分布具有對稱性，即正、負風向角對應的結果一致.以燈罩形心作為氣動力的監控點，計算結果如圖8、圖9所示.

新增吊索截面的平均阻力系數和平均升力系數如圖8所示.為了便于和上一節的計算結果進行比較，特征尺寸仍取既有吊索直徑，坐標系選用體軸坐 標系.當風向角為0°時，兩截面阻力系數差異較大，LED 燈的存在使 截 面的阻力系數平 均 值降 低了45.9%;兩截面升力系數平均值均接近零.隨著風向角增大，兩截面阻力系數平均值的差異有所減小.但是，當風向角達到14°時，阻力系數的差異又再次增大，且升力系數的差異也逐漸增大.

新增吊索截面的升力系數均方根值如圖9所示.同時，對升力系數時程曲線進行了頻譜分析，根據其卓越頻率換算了對應的斯托羅哈數St.兩截面 升力系數均方根值的差異在0°時最明顯，隨著風向角從0°增大至30°，兩者差異逐漸減小.St數隨風向角的變化呈現相反的規律，當風向角介于0°～5°時，兩截面的旋渦脫落頻率較為接近.隨著風向角增加，兩截面的旋渦脫落頻率的差異增大，但當風向角接 近30°時，差異又逐漸減小.

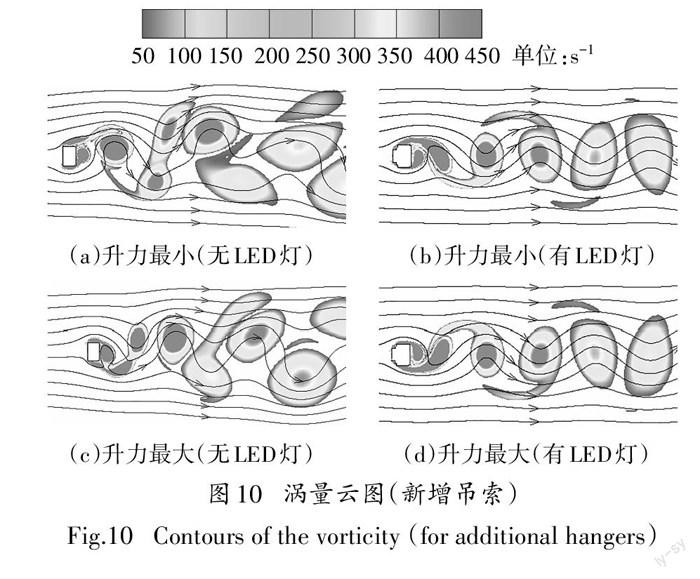
圖10給出了0°風向角時，新增吊索截面升力達到最大（方向向上）及最小（方向向下）時流場的渦量云圖.雖然兩個計算截面的旋渦脫落頻率較為接近，但渦量云圖卻有較大的差異.無LED 燈的截面近似 矩形，來流風在燈罩兩側倒角處發生了分離，使截面 上、下側的渦量較大，即升力系數均方根值較大.同時，來流分離所導致的旋渦具有較大的尺寸和強度，且緊貼截面右側，使阻力系數較大.尾流區域內，脫 落旋渦的分布較為雜亂.有LED 燈時，來流風在LED 燈兩側就發生了分離.LED 燈與燈罩之間形成的凹角起到了一定的導流作用，使截面上、下側的渦量降 低，即升力系數均方根值減小.同時，尾流側旋渦的尺寸和強度有所減小，使截面阻力系數減小.尾流區域內，脫落旋渦的分布也變得規則.

3 吊索的渦振響應分析

上一節通過二維數值模擬研究了亮化燈具對吊索截面旋渦脫落特性的影響，考慮了燈罩上有、無LED 燈兩種組合截面，并定性評價了不同風向角下兩者尾流中旋渦分布及發展規律的異同.實際上，局 部 LED 燈對流場的影響是三維的，還有局部抱箍的影響.本節將通過風洞試驗對前述現象進行驗證，并 進一步評價吊索的渦振性能.

3.1? 既有吊索的渦振響應

結構的渦激共振響應與結構的模態頻率有密切 聯系.既有吊索安裝亮化燈具后，質量的變化，會導 致其模態頻率發生變化.

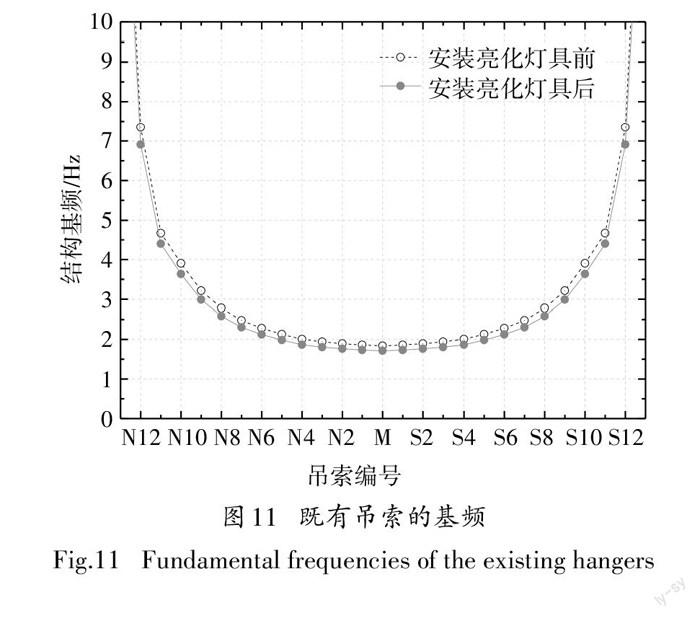
采用通用有限元軟件 ANSYS對各既有吊索的模態頻率進行了計算分析，用LINK10單元模擬吊索，吊索內力通過設置初應變的方式施加.各吊點處含有兩根吊索，但兩根吊索之間沒有相互連接，故建模時只考慮其中一根.亮化燈具的質量需考慮燈罩和電纜兩部分，通過質量點單元進行模擬.安裝亮化燈具前后，各吊索的一階模態頻率如圖11所示.其中，橫軸為吊索的編號.可以看到安裝亮化燈具后吊索的模態頻率略有減小.

試驗在西南交通大學 XNJD-1風洞高速試驗段 進行，通過節段模型動力試驗測試既有吊索安裝亮化燈具后的渦振性能.試驗模型長度2.095m，按照1∶1的幾何縮尺比制作，即吊索直徑為97 mm，燈罩高34 mm，寬60mm，根據實際間隔在模型上布置 LED 燈模型，如圖12所示.以跨中處的吊索為模擬對象，考慮到實際吊索的質量偏大，降低了模型的質量，具體參數見表3.其中，無燈模型為沒有安裝燈具的吊索模型，其測試結果僅作為對比參考，沒有調整 測試系統的阻尼比;有燈模型為安裝燈具的吊索模型，略增大了測試系統的阻尼比，使模型與原型的Sc數（Sc=4πmξ/ρD2，其中m為每延米質量;ξ為阻尼比;ρ為空氣密度;D為橫風向特征尺寸，取圓截面直徑）比值為0.81.

試驗中采用激光位移計測試了安裝亮化燈具的吊索的位移響應.測試風向角包括0°、15°、30°、45°，吊索的豎向振幅隨試驗風速的變化規律如圖13所示.其中，0°風向角時來流風垂直于橋軸線.當風向角為45°時，考慮到同一吊點處兩根吊索相互之間可能產生的氣動干擾，試驗中在測試索的上游設置了另一根未安裝亮化燈具的吊索.

當風向角為0°時，無燈具吊索在風速為1m/s時出現了渦激共振現象，安裝燈具后的吊索在試驗風速范圍內未出現明顯的渦激共振現象.結合上一節數值模擬的結果可知，安裝燈罩后截面升力的均方根值明顯減小，且 LED 燈的間隔布置以及抱箍的設置使得不同截面脫落旋渦的強度、頻率不一致，這些 差異降低了吊索整體發生渦激共振的可能性.

在斜風來流作用下，安裝燈具后的吊索則出現了明顯的渦激共振現象.具體情況如下：當風向角增大至15°時，吊索在風速1.20m/s 左右發生了渦激共振現象，但振幅有限，最大值為3.9mm.當風向角增大至30°時，吊索在風速1.27 m/s 左右發生了渦激共 振現象，且振幅明顯增加，最大值為117.8 mm，達到了吊索直徑的1.21倍.當風向角繼續增大至45°時，受上游側未安裝燈具的吊索尾流的影響，安裝燈具的下游索在風速1.4 m/s 左右發生了渦激共振現象，振幅雖有減小但仍然明顯，最大值為38.1mm，達到了吊索直徑的0.39倍.

試驗中以跨中處最長的吊索為對象進行了測 試，據此換算其余吊索的渦振鎖定風速.以風向角30°為例，試驗索在1.27 m/s 風速下發生了明顯的渦 振現象，其豎向位移時程的卓越頻率為1.750Hz.取 吊索直徑為特征尺寸，可得組合截面的斯托羅哈數St為0.134.基于St相同，可根據其他吊索安裝燈具 后的模態頻率換算對應的渦振鎖定風速，如圖14所示.其中，吊索的各階頻率按照弦理論公式進行計算.由計算結果可知，安裝亮化燈具后，吊索的模態 頻率略有降低，但組合截面的斯托羅哈數明顯減小，故導致各吊索的渦振鎖定風速有所提高.跨中附近 吊索基頻所對應的渦振鎖定風速小于2m/s，此時來 流風能量有限，且通常較紊亂，在一定程度上會弱化渦振響應，但應注意可能的高階渦振.

3.2 新增吊索的渦振響應

新增吊索不參與結構受力，其主要作用是固定 亮化燈具.因此，新增吊索的面積遠小于既有吊索，燈具的安裝方式也不同于既有吊索.如前所述，新增吊索被亮化燈具的外殼所包裹，其剛度由吊索提供，而氣動力由亮化燈具決定.為了保證新增吊索上亮化燈具的正常工作，其抗風穩定性也是需要關注和考 慮的.假設新增吊索的初始應變與鄰近位置處既有吊索一致，由此確定新增吊索的初始張拉力T0.然后，將此張拉力分別折減至0.75、0.50、0.25倍，并通過弦理論公式計算新增吊索的模態頻率，如圖15所示.

新增吊索的模態頻率低于既有吊索，跨中處吊索長度最大、模態頻率最小.較大的初始張拉力可以在一定范圍內提高新增吊索的模態頻率，但其值仍 然小于既有吊索.需要注意的是，雖然張拉力的具體數值不大，但由于新增吊索凈面積較小，過大的張拉力可能導致新增吊索應力過大，且對兩端的約束也會提出更高的要求.

在上一節的分析中，已得到新增吊索截面的斯 托羅哈數St，可根據各新增吊索的模態頻率換算對應的渦振鎖定風速.其中，特征尺寸采用了既有吊索的直徑，即97 mm.在數值計算中，考慮了燈罩上有、無LED 燈兩種情況，當風向角為0°時，無LED 燈截面的St=0.21，有LED 燈截面的St=0.26，據此區間換算得到的渦振鎖定風速如圖16中虛線所包絡的范圍;當風向角為30°時，無LED 燈截面的St=0.23，有LED燈截面的St=0.25，據此區間換算得到的渦振鎖定風速如圖16中實線所包絡的范圍.由前述關于既有吊索的分析可知，在某風攻角來流作用下，若有、無LED 燈這兩種截面的旋渦脫落特性接近，則吊索更 容易發生渦激共振現象.對于新增吊索而言，30°風向角下兩截面的斯托羅哈數更為接近，吊索發生渦 激共振的可能性更高.總體來看，新增吊索的基頻較 低，對應的渦振鎖定風速很小，但需要注意可能出現的高階模態渦激共振現象.此外，由于新增吊索非常 輕柔，除了渦振響應外，其在脈動風作用下的抖振問 題也不容忽視.為了提高其抗風性能，有必要進行氣動優化設計，或增加橫向連接索等結構優化措施，利用相鄰的既有吊索提供一定的約束，如圖17所示，但措施具體效果還有待進一步驗證.

4結論

本文以某座中承式拱橋的亮化方案為背景，研究了吊索渦振性能的改變，得到以下主要結論：

1）亮化改造使既有吊索的氣動外形發生根本性 改變，相當于圓形和矩形構成的組合截面.組合截面的繞流行為受風向角影響明顯，當風向角較小時，來 流在燈罩兩側倒角處發生分離并在吊索表面再附 著，減小了旋渦脫落的強度和頻率.當風向角較大時，來流經過吊索和燈罩之間的間隙并產生加速效應，增強了旋渦脫落的強度.

2）當來流垂直于橋軸線時，安裝燈具后既有吊索發生渦激共振的可能性較小.究其原因，一方面是 組合截面升力均方根值明顯減小，另一方面是燈罩 上間隔設置的LED燈使索軸向不同截面的旋渦脫落 頻率、強度出現了差異.當來流與橋軸線呈現一定夾角時，安裝燈具后既有吊索發生渦激共振的可能性增大.這是因為斜風作用下組合截面升力均方根值較大，且 LED燈對流場的影響有所減弱.

3）因不參與結構受力，新增吊索非常輕柔，其基 頻對應的渦振鎖定風速很小，但吊索在高風速下的高階模態渦振問題及抖振問題不容忽視.增大初拉力對新增吊索模態頻率的提升有限，還可能導致吊索自身及兩端連接件的強度問題.為了提高其抗風 性能，在設計時有必要考慮抑振措施.

4）既有吊索安裝亮化燈具后，兩種計算截面的升力系數在0°風向角附近出現了負斜率，且對應的馳振臨界風速很低，但在試驗中未觀測到模型的馳 振現象.這可能與不同截面旋渦脫落特性的差異有關，使吊索整體的準定常氣動特性與各截面有所差 異，還應該開展三維動態模擬進一步研究.

參考文獻

[1]李壽英，陳政清 .斜拉橋拉索安裝亮化燈具的風致穩定性研究[J].工程力學，2008，25（S1）：94-98.

LI S Y，CHEN Z Q.Aerodynamic stability of cables with lamps of cable-stayed bridge[J].Engineering Mechanics，2008，25（S1）：94-98.（In Chinese）

[2]董國朝，陳政清，羅建輝，等.安裝亮化燈具導致的斜拉橋拉索風致馳振流固耦合分析[J].中國公路學報，2012，25（1）：67-75.

DONG G C，CHEN Z Q，LUO J H，et al.Fluid-structure interac-tion analysis of wind-induced galloping of cables with lamps ofcable-stayed bridge[J].China Journal of Highway and Trans-port，2012，25（1）：67-75.（In Chinese）

[3]徐升橋，劉永鋒.京新上地斜拉橋的技術創新[J].鐵道標準設計，2013，57（3）：29-34.

XU S Q，LIU Y F.Technological innovation on Shangdi cable-stayed bridge on Beijing-Xinjiang highway[J].Railway Standard Design，2013，57（3）：29-34.（In Chinese）

[4]周傲秋，余海燕，許福友.亮化燈具安裝后斜拉索三維氣動性能試驗研究[J].大連理工大學學報，2019，59（4）：379-384. ZHOU A Q，YU H Y，XU F Y.Experimental study of aerody-namic performance of3D stay cables with lighting lamp[J].Jour-nal of Dalian University of Technology，2019，59（4）：379-384.（In Chinese）

[5]鄧周全，唐浩俊，李永樂，等.亮化燈具對既有斜拉索風致振動影響的試驗研究[J].振動與沖擊，2020，39（6）：44-50.?????? DENG Z Q，TANG H J，LI Y L，et al.Experimental research on the wind-induced vibration of stay cables with lighting fixtures[J].Journal of Vibration and Shock，2020，39（6）：44-50.（In Chinese）

[6]DENG Z Q，TANG H J，HU B，et al.Aerodynamic instability of

stay cables with lighting fixtures[J].KSCE Journal of Civil Engi-neering，2021，25（7）：2508-2521.

[7]NORBERG C.Fluctuating lift on a circular cylinder：review and

new measurements[J].Journal of Fluids and Structures，2003，17（1）：57-96.

[8]MA W Y，LIU Q K，MACDONALD J H G，et al.The effect of sur-face roughness on aerodynamic forces and vibrations for a circular cylinder in the critical Reynolds number range [J].Journal of Wind Engineering and Industrial Aerodynamics，2019，187：61-72.

[9]王漢封，鄒超，王啟文，等.均勻流中懸臂圓柱體氣動力雷諾數效應[J].湖南大學學報（自然科學版），2015，42（5）：65-71.WANG H F，ZOU C，WANG Q W，et al.Reynolds number effects on the aerodynamic forces of a cantilevered circular cylinder in uniform flow [J].Journal of Hunan University（Natural Sci-ences），2015，42（5）：65-71.（In Chinese）

[10]BRUNO L，SALVETTI M V，RICCIARDELLI F.Benchmark on

the aerodynamics of a rectangular 5 ∶1cylinder：an overview after the first four years of activity[J].Journal of Wind Engineering and Industrial Aerodynamics，2014，126：87-106.

[11]沈國輝，錢濤，羅蔣皓，等.不同長寬比矩形截面高層建筑的風荷載研究[J].湖南大學學報（自然科學版），2015，42（3）： 77-83.

SHEN G H，QIAN T，LUO J H，et al.Study of wind loading on rectangular high-rise buildings with various length-to-width ratios[J].Journal of Hunan University（Natural Sciences），2015，42（3）：77-83.（In Chinese）

[12]WU B，LI S P，LI K，et al.Numerical and experimental studies on

the aerodynamics of a 5 ∶1rectangular cylinder at angles of attack[J].Journal of Wind Engineering and Industrial Aerodynamics，2020，199：104097.

[13]詹昊，李萬平，方秦漢，等.不同雷諾數下圓柱繞流仿真計算[J].武漢理工大學學報，2008，30（12）：129-132.

ZHAN H，LI W P，FANG Q H，et al.Numerical simulation of the flow around a circular cylinder at varies Reynolds number[J].Journal of Wuhan University of Technology，2008，30（12）：129-132.（In Chinese）

[14]畢繼紅，余化軍，任洪鵬.靜止方柱和圓柱繞流的二維數值分析[J].三峽大學學報（自然科學版），2012，34（1）：41-45.

BI J H，YU H J，REN H P.Two dimensional numerical simula-tion of flow over a static square cylinder and a static circular cylin-der[J].Journal of China Three Gorges University（Natural Sci-ences），2012，34（1）：41-45.（In Chinese）

[15]ROSHKO A.Experiments on the flow past a circular cylinder at

very high Reynolds number [J].Journal of Fluid Mechanics，1961，10（3）：345-356.

[16]SELVAM R P.Finite element modelling of flow around a circular

cylinder using LES[J].Journal of Wind Engineering and Indus-trial Aerodynamics，1997，67/68：129-139.

[17]ADACHI T.Effects of surface roughness on the universal Strou-hal number over the wide Reynolds number range[J].Journal of Wind Engineering and Industrial Aerodynamics，1997，69/70/71：399-412.