基于Boosted-Gold 算法的γ 能譜反演分析*

張雙 賀三軍 廖峰 羅萬 周芷千 高波 劉麗艷 趙修良

(南華大學核科學技術學院,衡陽 421001)

為了利用低能量分辨率探測器γ 能譜分析獲取未知放射性核素的特征信息,提高γ 能譜中重峰及弱峰分析的準確性和有效性,本文開展了基于Boosted-Gold 算法的NaI(Tl)探測器γ 能譜分析研究.采用MCNPX建立NaI(Tl)探測器模擬模型,獲得了維度201×200 的探測器響應矩陣.基于Boosted-Gold 算法開發了γ 能譜反演程序.實驗測量了γ 源22Na,133Ba 和152Eu 的探測器響應能譜,并以不同γ 射線能量、不同能差 (ΔE)、不同相對強度為條件構建了3 組低分辨率模擬γ 能譜,結合響應矩陣及反演程序對實測γ 能譜和模擬γ 能譜進行反演.以IAEA 數據庫核素標準特征信息對反演結果進行分析.結果表明:Boosted-Gold 算法對實測γ 能譜特征能量反演誤差最大為2.17% (133Ba 源0.276MeV),反演強度與標準強度最大差為0.197(152Eu 源1.408 MeV).對模擬γ 能譜核素特征能量均可準確分析,反演強度與標準強度差值保持在0.01 以內;當增強系數p≤14 時,Boosted-Gold 算法有利于γ 放射性核素的定量分析,對于相對強度大于10%的γ 射線,該算法具有更好的分析準確性.

1 引言

隨著γ能譜分析技術在核應急監測、核安全、環境輻射防護等應用領域的深化擴展,對γ能譜分析核素特征信息的準確性和有效性提出更高的要求[1].目前NaI(Tl)探測器因其探測效率高、價格低、易維護等特點,大面積應用于一些實際條件下的γ能譜的測量[2],但受其能量分辨率限制以及測量環境本底等因素的影響,實測γ能譜常常表現為能量相近的射線形成復雜的重峰、強度較弱的核素全能峰完全淹沒于本底及康普頓效應當中[3,4],以上不利性態提高了輻射特征信息的分析難度,目前針對低能量分辨率γ能譜的定性定量分析準確性低[5],尤其針對弱峰的定量分析誤差可達34%以上[6].因此如何實現重峰及弱峰的分離和識別、提高低分辨率γ能譜分析的準確性和有效性是目前急需解決的問題.

能譜反演技術用于γ能譜分析可有效提高其能量分辨率,增強低分辨率γ能譜核素特征信息的易讀性[7,8].現已提出多種γ能譜反演算法,如奇異值分解(singular value decomposition,SVD)算 法[9],最大似然-期望最大化算法(maximum-likeli-hood expectation maximization,ML-EM)[10],Gold 算 法[11],直接解調法(direct demodulate method,DDM)等[12];其中ML-EM 和Gold 算法因具有全局收斂性、解的非負性、收斂速度快等特性,是目前最有效且常用的反演算法[10,11,13];然而Gold 算法相較ML-EM 算法在理解掌握和開發方面更具優勢[14,15];在Gold 算法基礎上提出的Boosted-Gold 算法[16],進一步提高了收斂速度,解決了前者收斂穩定后無法更進一步提升能譜分辨率的問題.

目前國內外學者分別對多種算法在不同探測器、不同領域下的運用做了驗證性研究[9-16],2009 年Rahmand 等[3]將ML-EM 算法用于水下γ放射性核素監測系統的能譜分析,結果表明γ能譜峰總比提高,全能峰計數提高了5.29 倍;2016 年何劍鋒等[17]采用Gold 算法,以實測能譜數據驗證了采用高斯響應矩陣對γ能譜進行分析的可行性;2019 年,趙日等[18]采用Gold 算法運用于全身計數器γ能譜分析,與Genie2000 軟件分析結果比較,表明反演算法優于傳統全能峰法;2021 年張雙佼等[19]將one-fold Gold 算法用于EJ309 液體閃爍體探測器的響應譜反演,驗證了其用于γ能譜分析的可行性以及在n-γ分辨領域的應用潛力.然而更多工作只強調了反演算法用于特定領域γ能譜分析的可行性[17-22],尤其對于Boosted-Gold 算法用于低能量分辨率探測器γ能譜分析的應用研究并未見更多報道.因此,有必要對Boosted-Gold 算法應用于低分辨率探測器γ能譜分析,開展其重峰及弱峰分析的準確性和有效性研究;盡管本研究只針對了較低能量分辨率的NaI(Tl)探測器,但其應用范圍與實用性價值較大.

本文為了提高低分辨率探測器γ能譜重峰及弱峰分析的準確性和有效性,開展了基于Boosted-Gold 算法的NaI(Tl)探測器γ能譜反演研究,以期實現對入射γ射線的準確定性定量分析,為利用低分辨率探測器在未知放射性核素的種類及強度分析中提供技術支撐.

2 理論及算法開發

理論上,某一特征能量的γ射線的能譜表現為線狀譜[23],即只在特征能量存在幅值,能譜反演的目的是由譜儀測量的脈沖響應譜求解γ射線本征譜,實現γ射線的定性定量分析.入射γ射線與脈沖響應譜之間的關系可如(1)式所示[2,11]:

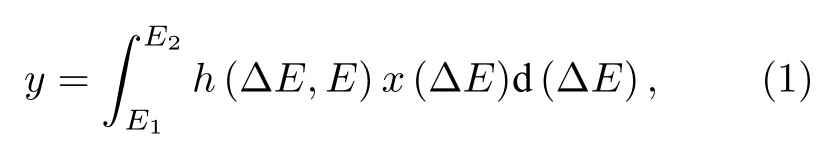
其中x為入射譜;y為脈沖響應譜;h(ΔE,E) 為探測器的響應函數,表示所測能量為 ΔE的單位能量的γ射線對應于脈沖響應譜中能量E處的相應計數.當h(ΔE,E) 與x(ΔE) 均可積條件下,(1)式可進一步離散化為

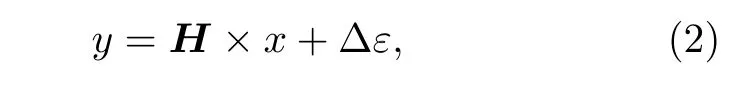
其中 Δε為γ射線測量過程中的誤差;H為探測器響應矩陣,如下所示:

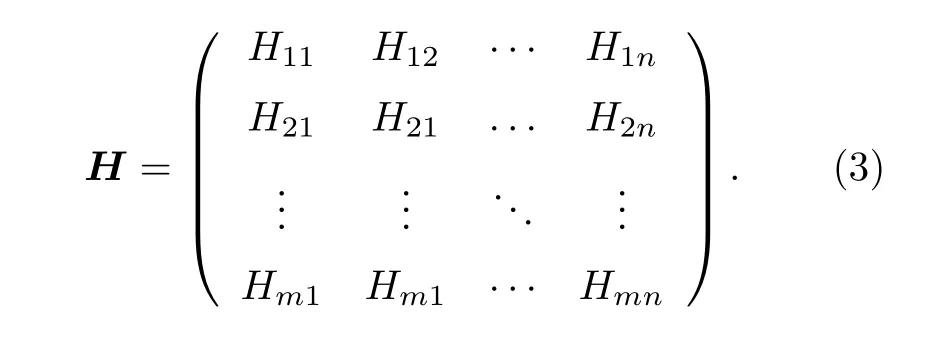
維度m,n分別由響應函數離散化程度與步長確定.根據(2)式和(3)式,函數(1)可離散化為

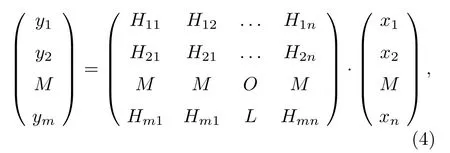
其中誤差項 Δε包涵于響應矩陣H中.由于(4)式中誤差項的存在以及H中各列之間的強關聯性[13],使得該方程組解的問題實際是不適定問題,采用直接求逆方法無法求出有意義的解,通常由特殊反演算法得到待求解.

為了準確求解(4)式,Boosted-Gold 反演算法[16]中以HT左乘(2)式,引入局部松弛系數μ,建立如下迭代過程:

其中n 為構成響應矩陣的響應函數個數,將滿足收斂條件解x 的各分量 進行如(7) 式的冪指數非線性增強,并將其作為迭代初值再一次進入(6) 式迭代計算,最終得到滿足收斂條件的解.

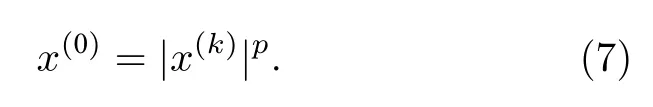
上式中p＞ 1,為冪指數增強系數;根據(6)式和(7)式對算法進行開發,過程如圖1 所示:

如圖1 所示,算法迭代過程如下:

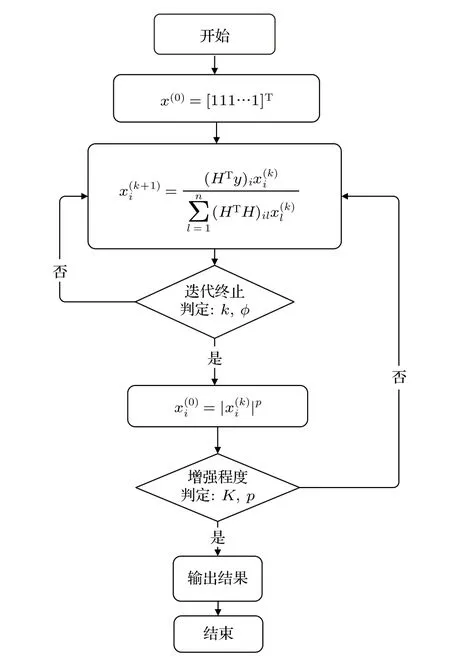
圖1 Boosted-Gold 算法計算過程Fig.1.The calculation process of Boosted-Gold Algorithm.

a) 首先,給定初值x(0)、迭代次數k以及迭代終止判定條件φ.

b) 其次,進入迭代過程并進行迭代終止判定.

c) 再次,設定增強次數K及增強系數p進行再一次迭代并進行迭代終止判定.

d) 最后輸出結果.

其中初值x(0)中的各分量設定為1;迭代判別條件如(8)式所示:

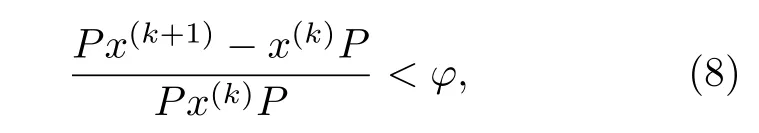
式中,x(k)為第i次迭代結果,x(k+1)為第i+1 次迭代結果;φ為給定的迭代殘差精度.

3 探測器刻度及響應矩陣的獲取

3.1 實驗系統及γ 能譜測量

γ能譜測量實驗系統主要由FJ374 型NaI(TI)閃爍體探測器(40 mm×40 mm),BH1283N 型高壓電源,BH1218 型線性放大器(FH0001A 型 機箱),ADC 多道脈沖幅度分析器以及PC 搭建,如圖2 所示.實驗中γ源到探測器探頭的距離為1.5 cm,高壓電源電壓為420 V,主放放大倍數為20,測量時間120 min,輸出信號由4096 道ADC多道脈沖幅度分析器進行數據采集并在PC 端顯示;最后對標準γ源22Na,60Co,133Ba,137Cs 和152Eu脈沖響應譜進行了測量,并在相同實驗條件下測量了環境本底用于后續數據處理.

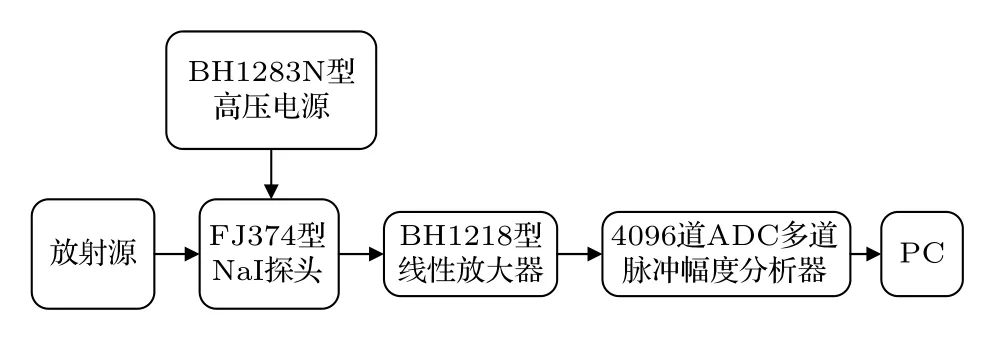
圖2 實驗平臺電子學框圖Fig.2.The electronics block diagram of the experimental platform.

3.2 NaI(Tl)探測器能量刻度和分辨率刻度

探測器的能量刻度和分辨率刻度是γ能譜分析的依據,也為NaI(TI)探測器蒙特卡羅建模提供準確參數.能量刻度函數由γ射線的全能峰峰位與對應的特征能量線性擬合獲得.為了準確獲得標準γ源22Na,60Co,133Ba 和137Cs 全能峰的峰位以及半高寬(FWHM),首先根據實測自然本底對實驗能譜進行了本底計數扣除;然后采用Savitzky-Golay 方法對譜數據進行了3 點平滑濾波,消除探測器對γ射線響應統計過程中統計漲落的影響;最后采用一階導數尋峰方法,獲得所測γ源全能峰峰位及半高寬信息;能量刻度如圖3 所示.

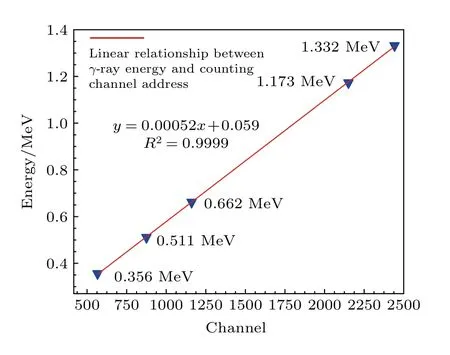
圖3 FJ374 型NaI(Tl)探測器能量刻度Fig.3.Energy calibration of FJ374 NaI(Tl) detector.

圖3 中能量刻度函數表征了全能峰峰位(N)與入射γ射線特征能量(Eγ)的線性關系.如(9)式所示:

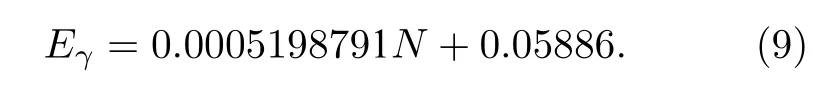
能量分辨率與入射γ射線的能量相關,因此能量分辨率刻度由γ射線特征能量與響應譜對應全能峰半高寬(FWHM)完成,函數表達式如(10)式所示[24]:

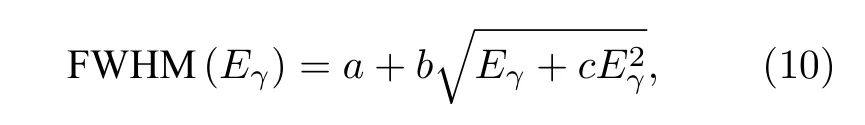
其中a,b,c為待定展寬參數.Eγ為全能峰對應的入射γ射線特征能量,單位為MeV;根據實測標準γ源特征能量及對應全能峰半高寬信息進行非線性待參擬合,獲得(10)式待定參數a=0.01607,b=0.02729,c=1.28065,如圖4 所示.

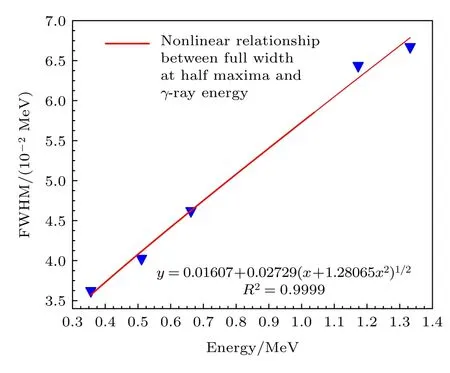
圖4 能量(Eγ)與半高寬(FWHM)對應關系Fig.4.The correspondence between energy (Eγ) and halfmaximum width (FWHM).

3.3 響應矩陣的計算

響應矩陣的準確性和反演算法的穩定性是進一步降低分析偏差的兩方面.為了準確獲得NaI(TI)探測器響應矩陣,采用MCNPX 模擬程序構建了探測器模型,建模參數與實驗條件保持相同,其中入射γ射線源為點源,與探測器探頭距離為15 mm,探測器靈敏體積為厚40 mm、直徑40 mm 的柱型,外層鋁殼厚度為1.5 mm,反光層MgO 厚度為1.5 mm,如圖5 所示.

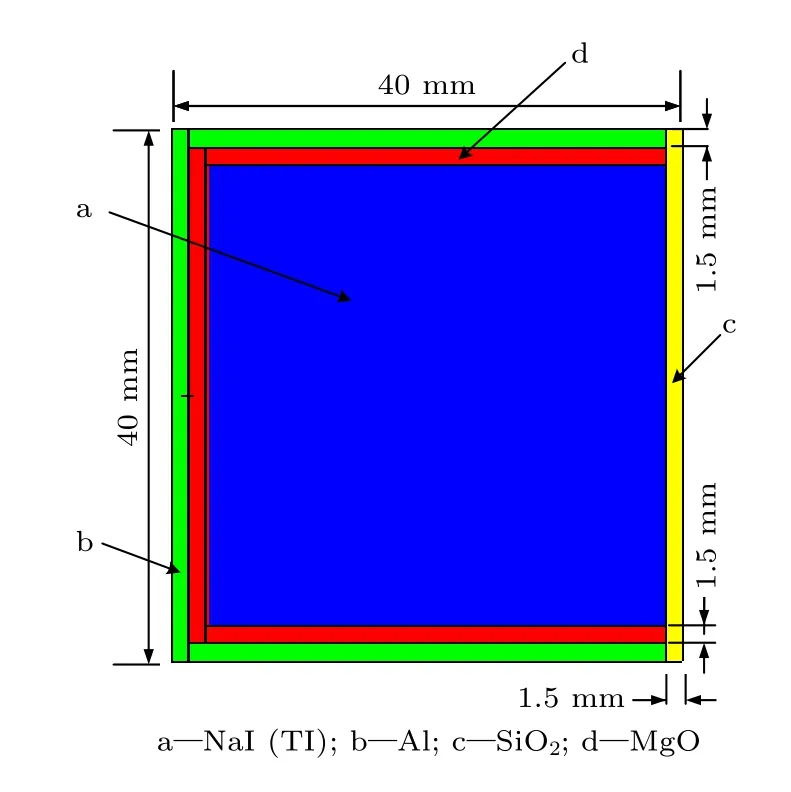
圖5 FJ374 型NaI(Tl)探測器仿真模型Fig.5.The simulation model of FJ374 NaI(Tl) detector.

將每個入射單能γ射線響應函數作為構建響應矩陣一個列向量,共由200 個單能γ射線的響應函數列向量構成;模擬過程采用F8 計數卡進行計數抽樣為200 道,抽樣能量范圍為0—2 MeV;各單能γ射線能量隨步長0.01 MeV,覆蓋能量區間為0.01 至2 MeV;采用(10)式對模擬響應函數進行展寬,最終得到維度為201×200 的響應矩陣,結果如圖6 所示.

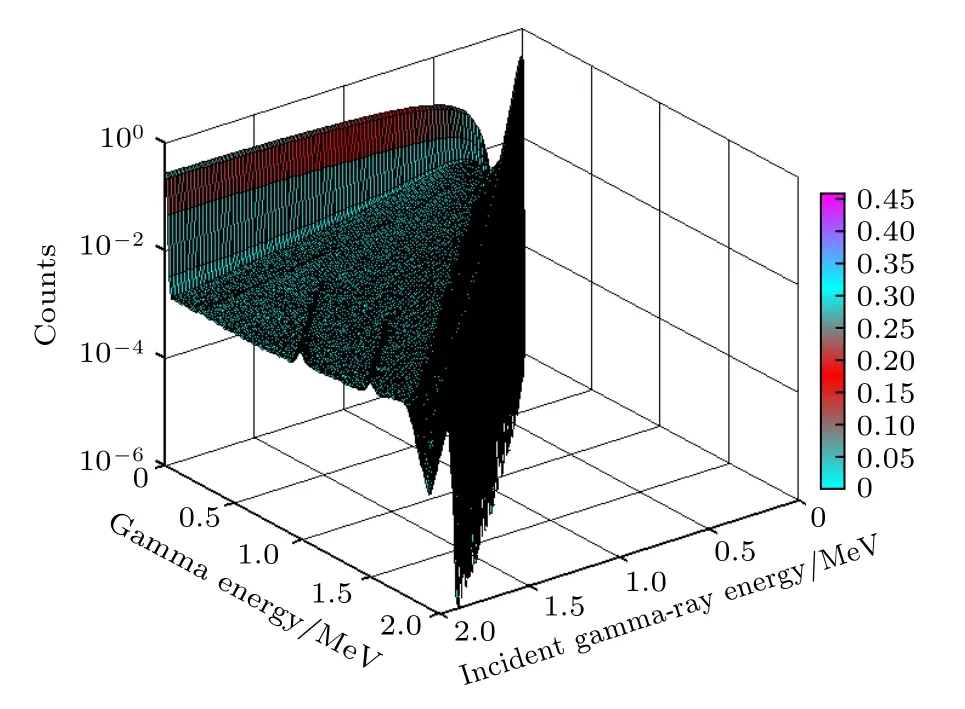
圖6 NaI(TI)探測器響應函數Fig.6.Response matrix for the NaI (TI) detector.

4 γ 能譜反演

4.1 Boosted-Gold 算法反演低能量分辨率γ 能譜的準確性

為了驗證Boosted-Gold 算法反演低分辨率γ能譜重峰和弱峰分析的準確性,根據開發的反演算法程序和計算的響應矩陣,對實驗測量標準γ源22Na,133Ba 和152Eu 脈沖響應譜進行反演,反演前后結果對比如圖7 所示.

由圖7 可見,圖7(a)中22Na 源只能清晰顯現能量為0.511 MeV 的γ射線全能峰,圖7(b)中133Ba源特征能量為0.223,0.303,0.384 MeV 的γ射線全能峰被完全淹沒,而圖7(c)中152Eu 源只有少數全能峰可見,經過反演后γ能譜全譜分辨率均明顯提高,全能峰準確顯現且峰面積計數可讀,對反演結果的準確性進行分析,如表1 所列,其中γ射線特征能量反演結果與標準值誤差由(11)式計算:

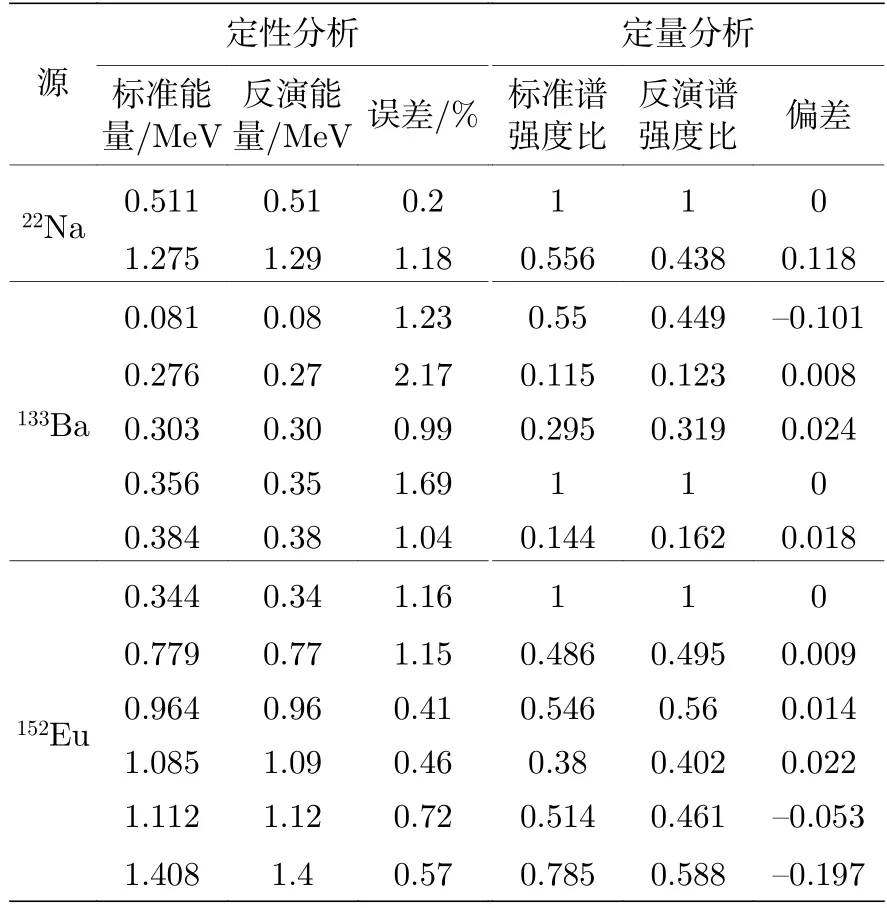
表1 實驗譜與反演譜結果分析對比Table 1.Analysis and comparison of the experimental spectrum and the unfolded spectrum results.

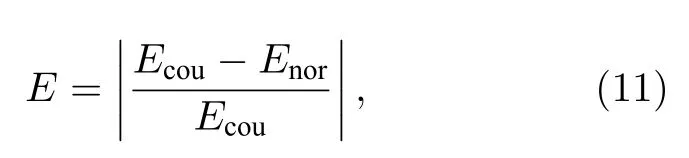
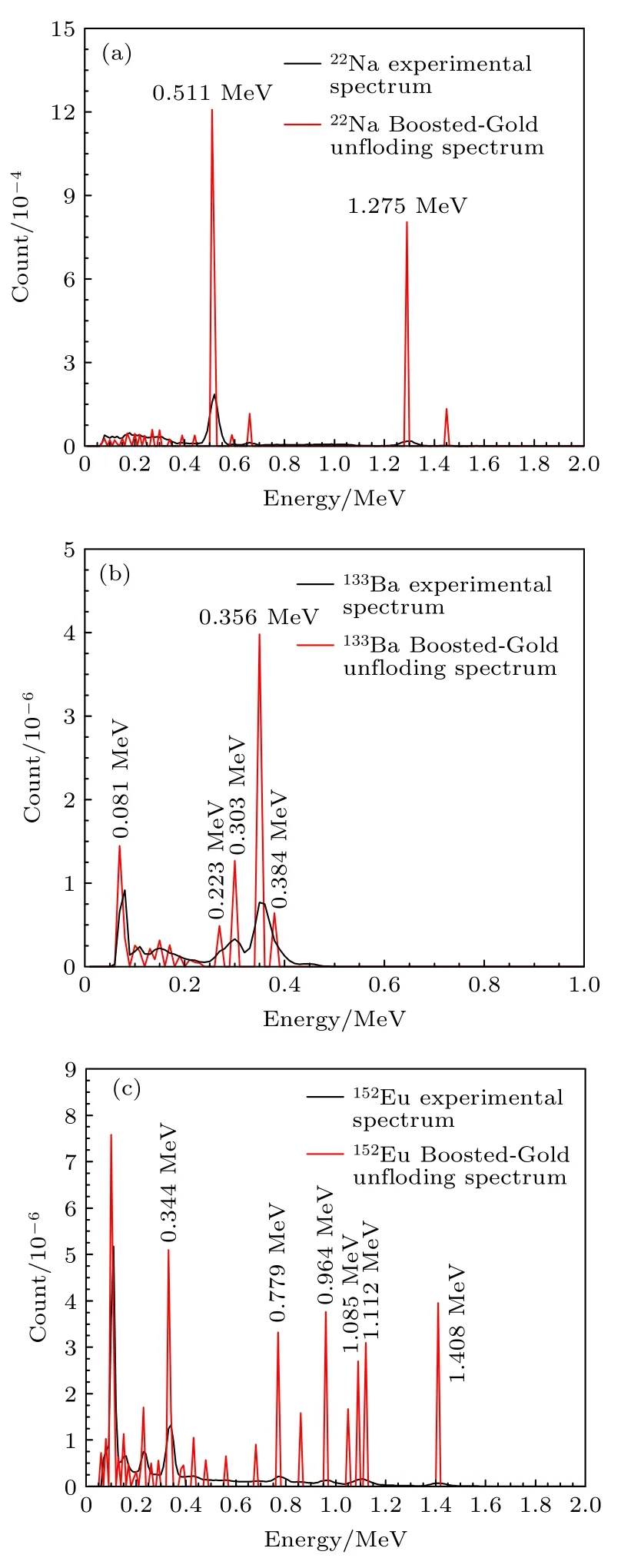
圖7 實測γ 能譜與反演能譜的比較 (a) 22Naγ 源能譜反演前后結果對比;(b)133Baγ 源能譜反演前后結果對比;(c)152Eu γ 源能譜反演前后結果對比Fig.7.The comparison between the measured γ energy spectra and the unfolded energy spectrum:(a) Comparison of the results before and after the unfolded of the energy spectrum of the 22Na γ source;(b) comparison of the results before and after the unfolded of the energy spectrum of the 133Baγ source;(c) comparison of the results before and after the algorithm unfolded of the energy spectrum of the 152Eu γ source.

式中,Ecou表示反演后的特征能量,Enor表示標準特征能量,反演強度分析中采用IAEA 核數據庫γ放射性核素各特征射線間絕對強度之比作為標準數據,用于驗證γ射線全能峰計數收斂結果的準確性.

表1 反演結果表明,γ射線特征能量反演誤差最大為2.17%(133Ba 能量為0.276 MeV).反演強度與標準強度最大偏差為0.197,除特征能量為1.275 MeV(22Na),0.081 MeV(133Ba),1.408 MeV(152Eu)的γ射線強度偏差大于0.1 外,其余γ射線反演強度偏差均小于0.06.

反演偏差主要由于以下原因:首先由于反演結果的準確性依賴于響應矩陣的準確性,因此蒙特卡羅模擬響應函數與實際響應函數的差異是造成反演結果偏差的一方面;其次,當低能區全能峰計數收斂不完全時,強度計算過程中認為γ射線特征能量相鄰道計數也屬于全能峰計數,一定程度上增加了強度計算與標準值的偏差;最后,受限于響應矩陣步長(0.01 MeV),當兩種γ射線能差小于響應矩陣步長時,將無法分析該兩種特征γ射線,強度反演結果將大于標準值,如對133Ba 的特征能量為0.079 和0.08 MeV 的γ射線分析.

4.2 Boosted-Gold 算法反演低能量分辨率γ 能譜的準確性和有效性

實測γ能譜反演結果驗證了Boosted-Gold 算法對低分辨率探測器γ能譜重峰和弱峰分析的準確性,為了進一步研究Boosted-Gold 算法用于低分辨率探測器γ能譜分析的準確性和有效性范圍,以MCNPX 建立的NaI(TI)探測器模型,根據γ射線不同相對強度、不同能量(Eγ)、不同能差(ΔE)模擬獲得了三組低分辨率探測器γ能譜,其中入射γ射線能量由(12)式確定[25]:

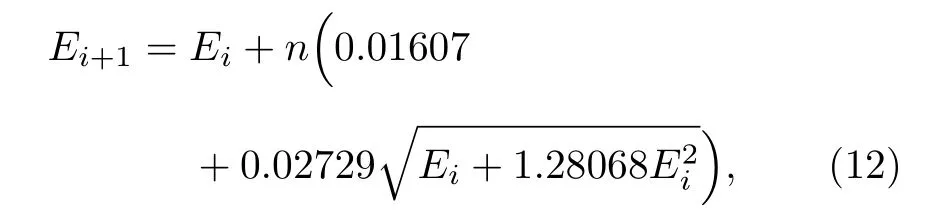
其中n取值為1,Ei為第i種單能射線能量,模擬譜分別有4,6 和8 種不同γ射線能量,獲得γ能譜射線最小能差為0.03 MeV,相鄰γ射線強度最大比為1:0.3;利用開發的反演算法程序和獲取的響應矩陣對模擬γ能譜進行反演;增強因子p=4,進行10 次增強過程,每次進行1000 次迭代,反演前后結果對比如圖8 所示.

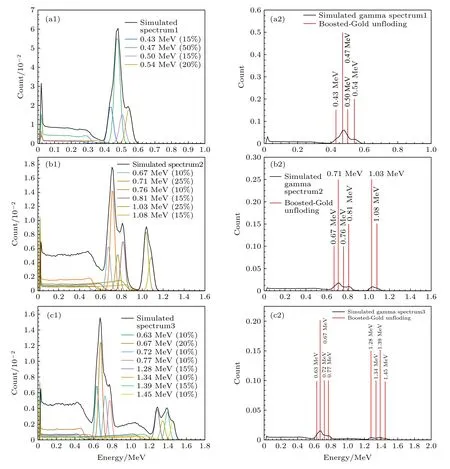
圖8 模擬γ 能譜反演前后結果對比 (a1) 4 種能量γ 射線模擬譜;(a2) 4 種能量γ 射線模擬譜反演前后結果對比;(b1)6 種能量γ 射線模擬譜;(b2) 6 種能量γ 射線模擬譜反演前后結果對比;(c1) 8 種能量γ 射線模擬譜;(c2) 8 種能量γ 射線模擬譜反演前后結果對比Fig.8.The comparison of between the results before and after the unfolding of the simulated γ energy spectrum:(a1) The simulation spectrum of gamma-rays of 4 energies;(a2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 4 energies;(b1) the simulation spectrum of gamma-rays of 6 energies;(b2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 6 energies;(c1) the simulation spectrum of gamma-rays of 8 energies;(c2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 8 energies.

如圖8(a1)、圖8(b1)和圖8(c1)三組混合γ能譜中,強度較弱的γ射線全能峰嚴重重疊甚至被相對強度較高的γ射線全能峰掩蓋,反演結果分別如圖8(a2)、圖8(b2)和圖8(c2)所示,各全能峰清晰顯現且計數均收斂于一道,入射γ射線能量及全能峰計數均可直接讀取,反演譜分析結果如表2 所列.

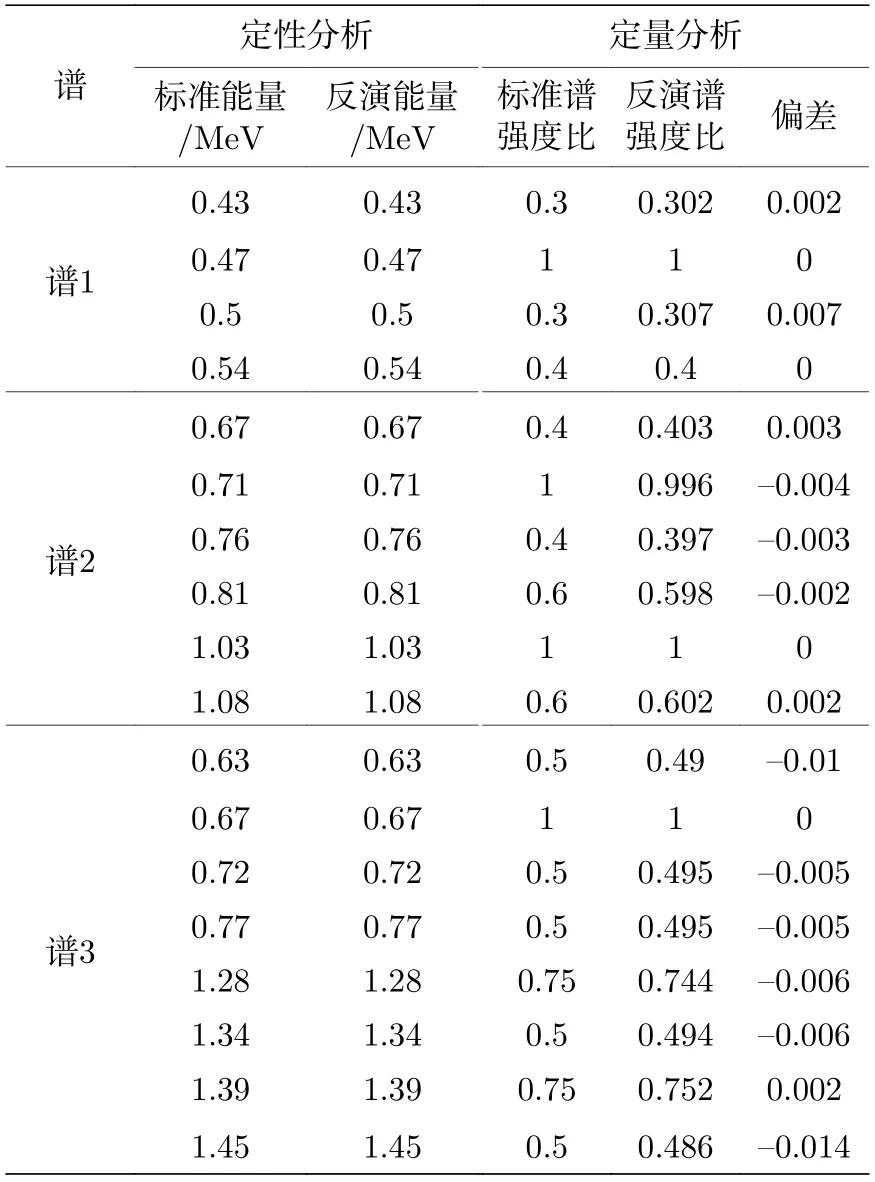
表2 模擬譜與反演譜結果對比Table 2.Comparison of the simulated spectrum and the unfolded spectrum results.

由表2 可知,γ能譜中被淹沒的全能峰均可被準確反演,γ射線反演能量與入射能量一致;反演強度與標準強度最大差為0.014,其余各全能峰反演強度與標準強度偏差均小于0.01.圖8(a1)中能量為0.5 MeV 的γ射線反演強度偏差最大為0.007,其余γ射線反演強度偏差均小于0.002.圖8(a2)中能量為0.71 MeV 的γ射線強度反演結果偏差最大為0.004,而能量為0.67 和0.76 MeV 的γ射線強度反演偏差為0.003.圖8(a3)中能量為1.45 MeV的γ射線強度反演偏差最大為0.014,且能量為1.28,1.34,0.67 和0.72 MeV 全能峰強度與標準強度偏差均大于0.005.可見,隨著入射γ射線增多,γ射線強度反演的準確性變小,且反演準確性與γ射線強度成正比.

當γ射線相對強度小于10%時,反演強度均小于標準強度,且相對強度越小,反演強度與準確強度偏差越大,造成這一結果的原因在于,反演過程中非線性冪指數增強系數p使得譜數據中占比較小的分量相對更小,導致迭代過程該分量更快向0 收斂,表現在反演結果中γ射線強度反演結果偏小,且γ射線相對強度越小偏差將越大.

4.3 增強系數p 對弱峰及重峰結構解析能力的影響

Boosted-Gold 反演算法中非線性冪指數增強系數p的引入是為了克服Gold 反演算法收斂穩定后無法進一步提升能量分辨率的問題;然而實驗發現,增強系數p在進一步提升γ能譜重峰和弱峰分離的同時,分析結果的準確性隨p變化較大,尤其對于相對強度小于10%的γ射線;為了進一步說明增強系數p對弱峰或重峰結構的解析準確性的影響,構建了能量和相對強度分別為0.43 MeV(3%),0.46 MeV(50%),0.5 MeV(5%),0.82 MeV(35%),0.87 MeV(7%)的低分辨率γ能譜,研究在不同p值下相對強度小于10%的γ射線反演結果的準確性,如圖9 所示.

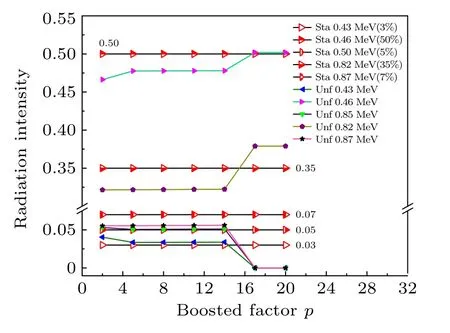
圖9 不同p 值下標準相對強度數據與反演數據的對比Fig.9.The comparison of the standard relative intensity data and the unfolded data at different p-values.

反演結果表明,當p≤14 時各γ射線強度的反演結果基本保持恒定,有利于γ能譜的分析,特別是弱峰;當p＞14 時,反演結果準確性降低,相對強度小于10%的γ射線全能峰計數進一步向0 收斂,相對強度較大的γ射線計數進一步增加,最終全譜只有相對強度較大的γ射線全能峰被保留且保持恒定,將無法完成相對強度小于10%的γ射線的分析識別.

5 結論

為了利用低能量分辨率探測器γ能譜分析獲取未知放射性核素的特征信息,提高γ能譜中重峰及弱峰分析的準確性和有效性,本文開展了基于Boosted-Gold 算法的NaI(Tl)探測器γ能譜分析研究.首先采用蒙特卡羅方法建立了NaI(TI)探測器模型,以此構建了NaI(TI)探測器響應矩陣;其次根據Boosted-Gold 算法理論開發了能譜反演程序;然后根據響應矩陣和開發的反演算法程序對模擬γ能譜和實測γ能譜進行反演;以實測γ源22Na(0.511 和1.275 MeV),133Ba(0.081,0.276,0.303,0.356 和0.384 MeV)和152Eu(0.344,0.779,0.964,1.085,1.112 和1.408 MeV)脈沖響應譜,驗證了Boosted-Gold 算法反演低分辨率探測器γ能譜的準確性;以不同γ射線相對強度、不同入射能量(Eγ)、不同能差(ΔE)構建了三組低分辨率探測器γ能譜,進一步驗證了其反演低分辨率探測器γ能譜重峰及弱峰的準確性和有效性;最后進一步明確了非線性增強系數p對重峰及弱峰結構分析準確性的影響.

實測γ能譜反演結果表明:Boosted-Gold 算法對γ射線特征能量反演誤差最大為2.17%(133Ba 能量為0.276 MeV);反演強度與標準強度最大偏差為0.197(152Eu 能量為1.408 MeV).能譜中γ射線強度最大比為1:0.115(133Ba 特征能量0.276 和0.356 MeV)、最小能差為0.03 MeV(133Ba 特征能量0.356 和0.384 MeV),表明Boosted-Gold 算法反演低能量分辨率探測器γ能譜可實現較準確的分析結果,尤其具有準確的定性分析能力.

模擬γ能譜反演結果表明:最多8 種γ射線能量、γ射線強度最大比為1∶0.3、能差為1 倍FWHM條件下,Boosted-Gold 算法能夠準確分析入射γ射線特征能量,γ射線反演強度與標準強度差值保持在0.01 以內;當γ射線相對強度小于10%時,反演準確性隨之降低,且強度反演準確性與γ射線強度成正比,表明Boosted-Gold 算法對于相對強度大于10%的γ射線具有更好的分析準確性,但分析準確性與增強系數p取值相關,在p≤ 14 時γ放射性核素的定量分析更準確,p＞ 14 時將無法完成相對強度小于10%的γ射線的定性定量分析.由于模擬γ能譜過程更接近理想物理過程,模擬γ能譜反演結果優于實測γ能譜反演結果,說明γ能譜測量過程中誤差對反演結果的準確性影響較大,γ能譜數據誤差校正與反演算法結合,將進一步提升低分辨率γ能譜反演分析精度.