基于光子計數激光雷達的自適應門控抑噪及三維重建算法*
陳松懋 蘇秀琴 郝偉? 張振揚3) 汪書潮3) 朱文華3) 王杰3)
1) (中國科學院西安光學精密機械研究所,中國科學院空間精密測量技術重點實驗室,西安 710119)
2) (海洋觀測與探測聯合實驗室(西安光機所部分),青島海洋科學與技術試點國家實驗室,青島 266200)
3) (中國科學院大學,北京 100049)
4) (山西大學,極端光學協同創新中心,太原 030006)
光子計數激光雷達技術具有極高的探測靈敏度與時間分辨率,是極端條件下高精度目標信息獲取的重要手段.由于該技術通過探測單光子級的回波能量實現對目標信息的三維重建,因此極易受噪聲干擾,導致成像質量嚴重降低.基于高速電子門控的距離選通技術雖然可以有效抑制噪聲,但存在參數設計依靠經驗、目標檢測區間窄等問題.本文提出一種在寬目標檢測區間條件下的目標信息提取及三維重建方法,首先通過對三維回波信息的獲取機理及其概率模型進行分析,獲取目標信息分布范圍并通過算法門控提取有效信息;再采用高效的圖像重建算法進一步提升三維重建的質量,從而具有比基于純硬件的去噪方法更強的抑噪能力.實驗結果顯示,在平均像素光子數僅為3.020,且信號噪聲比僅為0.106 的極端條件下,本文提出的目標信息提取方法可將信號噪聲比提升19.330 倍;再配合高效的圖像重建算法,距離圖像的重建信噪比相比于傳統的互相關算法提升了33.520 dB,大幅提升了強噪聲環境下高精度目標信息獲取的能力.
1 引言
相比于傳統的激光雷達技術,光子計數激光雷達具有單光子級靈敏度、皮秒級時間分辨率與高光子利用率等特點,因此在遠距離三維成像[1]、水下光學成像[2]等極端條件下展現出了遠超傳統技術的成像效果,并成為了近年來光學成像領域研究的熱點.該技術的成像過程如圖1(a)所示,激光器發射的脈沖經由發射光路照明目標區域,非合作目標漫反射的能量則由物鏡收集,再通過中繼透鏡與窄帶濾光片耦合至單光子探測器;探測器的響應信號與激光脈沖發射信號則分別由時間相關單光子計數(time correlated single photon counting,TCSPC)模塊的兩個皮秒級獨立計時通道記錄.根據光子計數原理,通過大量累積回波信息即可恢復出離散的回波波形[3],進而求取離散波形中所蘊含的距離信息;再配合掃描振鏡即可實現目標區域空間分布的信息,從而實現高精度的三維成像.最終獲得的三維回波信號如圖1(b)所示,每個像素均包含圖1(c)中所示的離散波形,其中橫軸由TCSPC離散的計時柵格構成,縱軸則表示每個柵格上的光子數.
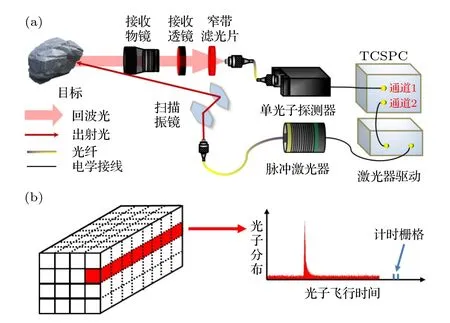
圖1 光子計數激光雷達原理圖 (a) 成像系統示意圖;(b) 三維回波示意圖Fig.1.The schematic diagram of photon counting LiDAR:(a) Description of the imaging system;(b) description of the three dimensional echo.
由于光子計數激光雷達極高的探測靈敏度在一定程度上克服了激光快速衰減特性帶來的挑戰,并可以通過累積的方式提高回波信號的信噪比,因此該技術成為了極端條件下光學成像的重要突破方向[4].但光子計數激光雷達技術同樣面臨著若干挑戰,如該技術的單次回波能量一般僅為單光子量級,故極易受到環境背景光與探測器暗電流等因素的影響,導致成像系統需大量累積回波信號以改善回波的信噪比;而長時間的累積則會大大降低成像速率,使其難以滿足實時化成像的需求.
為解決上述問題,2017 年Pawlikowska 等[5]將高速電子門控技術應用于單光子成像系統,通過控制探測器的開關實現距離選通,即只接收選通范圍內的回波信號,從而大幅抑制了后向散射與背景光等噪聲.該方法簡單易行,抑噪效果良好,因此基于高速電子門控的單光子成像系統被成功應用于水下[2]、濃霧[6,7]等強衰減強散射環境,并實現了超越人眼的成像能力.但為了保證信噪比,該方法的距離選通區間通常較窄,容易造成目標信息丟失,降低了對目標的檢測能力,且該方法依賴于人工選取門控的相關參數,即需大致知曉目標的位置.而未來的實際應用中目標的大致位置往往未知,故該技術在實用化方面仍有諸多限制.另一種思路則是Li 等[8]在2020 年提出的偏振去噪方法,該方法僅接收與發射光偏振態垂直的回波光子,實現噪聲的抑制.該方法無需進行距離選通,但會損失較多的能量,因此需根據具體的成像條件分析該方法的適用性.
除了硬件系統級的改進,通過采用先進的信號處理方法也可以有效改善成像質量.汪書潮等[9]提出了彈性變分模態提取算法,通過對一維的回波信號進行時頻分解實現信號去噪;2020 年,Halimi等[10]則基于非局部分析的思想提出了M-NR3D(multidimensional-nonlocal restoration of 3D) 算法,通過對三維回波的非局部空間聯系進行分析實現了稀疏且含噪信號的三維重建;與之類似的還有Tachella 等[11]在2019 年提出的ManiPoP 算法.相比于彈性變分模態提取等一維信號處理方法,圖像級重建算法功能更強大,效果相對更好,但若直接應用于目標檢測區間較寬的信號則存在重建時間長等問題,故一般先由人工截取目標范圍內的信號再由算法處理,使得該圖像重建算法一般僅扮演后處理的角色.
經過上述分析可知,目前光子計數激光雷達技術需要同時兼顧目標檢測區間寬度、信噪比及圖像重建速率的要求方能滿足未來實用化的需求.針對該問題,本文提出了一種基于自適應門控的光子計數激光雷達回波噪聲抑制及三維重建方法,首先基于對回波中信號與噪聲的統計特性分別建模以提取相關物理參數,并根據參數與統計模型自適應地感知并提取目標分布區間;再采用高效的圖像重建算法對算法門控后的信號進行處理,實現高精度目標信息的快速獲取.本方法不僅兼顧了信噪比、目標檢測區間寬度與重建速率的要求,同時還具有良好的自適應性,可根據不同成像條件與場景智能且穩定地感知目標信息,在水下成像、遠距離成像等極端環境中具有良好的應用前景.
2 目標信息感知
本文提出的自適應門控方法從回波中信號與噪聲的統計特性出發,通過對二者模型進行分析與處理提取特征參數,并根據特征參數與統計模型實現閾值的初始估計;再采用本文提出的基于模型與特征參數的估計方法進一步調整閾值以確定信息提取的范圍.
2.1 回波信號模型
令yi,j,t表示第i,j個像素中t時刻的回波光子數,其中i ∈[1,···,Nr] ,j ∈[1,···,Nc] ,t ∈[1,···,T],Nr,Nc,T分別表示三維回波的行數、列數與計時柵格數(見圖1).根據相關文獻與研究[3,10],yi,j,t具有泊松過程的特性,而根據泊松過程獨立增量與平穩增量的特點可將回波建模為信號與噪聲的加性混合模型,即有
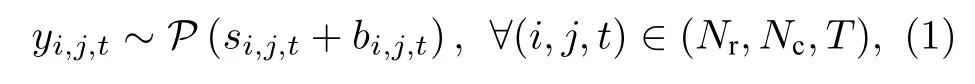
其中si,j,t與bi,j,t分別表示信號與噪聲在第i,j個像素中t時刻分布的期望.
根據光子計數成像機理可知,回波中所有的信號均源自短脈沖激光的照明,因此信號在回波時刻的分布上具有較好的一致性[12],且在較為理想的狀態下具有近似高斯分布的形狀.而噪聲的來源多樣,因此呈現較為隨機的分布.根據上述特點可將第i,j個像素中噪聲的期望bi,j建模為均勻分布,再將目標反射率ri,j與距離信息ti,j納入信號分布模型si,j,即有:

其中λ是一個 1×T且元素均為λ的向量,f表示成像系統的響應函數,一般可在對平板等特殊目標的標定過程中獲取.由于f是通過TCSPC 記錄,因此是若干計時柵格組成的離散波形.目前單光子雪崩二極管(single-photon avalanche diode,SPAD)因易于集成、可在室溫下工作等良好特性成為了主流的單光子探測器,其中SPAD 探測器的載流子在耗盡層中所產生的時間響應符合高斯分布的特性.然而,若光子在產生載流子之前先到達了探測器的中性區,則載流子會因為在耗盡層中的擴散產生具有指數分布特性的畸變,導致高斯分布模型無法準確描述f的波形[13,14].為了平衡模型描述的精確性與簡潔性,本文將f建模為雙指數分布模型,也稱為拉普拉斯分布模型[15,16],即有:
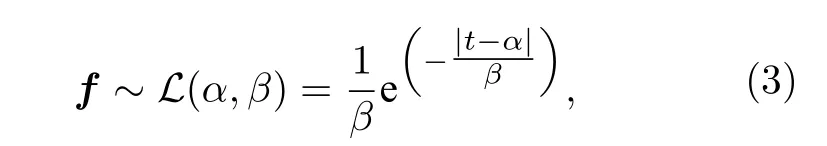
其中 |·| 表示絕對值,α和β分別表示雙指數分布的位置參數與尺度參數.
2.2 特征參數獲取
通過對大量實際場景中目標的分布規律進行歸納分析,可假設
1)在圖像獲取過程中目標在距離上的分布較為集中;
2)成像過程中成像環境并未發生劇烈變化;
3)掃描光斑的尺寸遠小于目標尺寸且每個像素的回波均為單峰信號.
在上述條件成立的情況下可以通過增加空間采樣的方式來彌補時間采樣的不足,即可以通過對三維回波信號在空間域(以下簡稱空域)求和以實現與時間累積后類似的效果.如圖2(a)所示,首先對三維回波直方圖中的N個像素(N=Nr×Nc)的回波在空域進行求和,即可得到一個 1×T的分布不包含空間分布信息,但包含著較為豐富的距離信息,故只需對進行深入分析(如圖2(b)所示)即可得到目標分布的大致范圍.
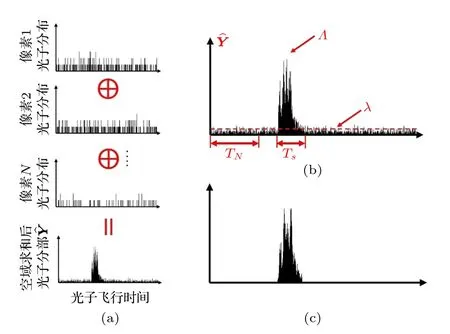
圖2 自適應信息提取過程示意圖 (a) 空域求和示意圖,其中 ⊕ 表示求和;(b) 特 征參數示意圖;(c) 目標信息的分布范圍Fig.2.The schematic diagram of adaptive information extracting:(a) Schematic diagram of the summing process on the spatial domain,where ⊕ stands for summing operation;(b) description of the feature parameters;(c) the distribution interval of the target.
本方法所需的主要特征參數如下:
1) 成像系統響應函數f中峰值的一半對應的寬度(已轉化為計時柵格數)γ.γ主要由發射激光的半高全寬(full width half maximum,FWHM)以及TCSPC 的計時精度(計時柵格的寬度)決定,代表信號模型中的特有屬性,具體則由f峰值的一半在橫軸的投影寬度得出.本文主要針對窄脈沖激光建模,對于γ較大的情況,則通過γ=log10(γ)」對脈寬進行修正,其中Γ表示作為參考的短脈沖的脈寬,則代表向下取整操作.上述兩個參數與(3)式中的尺度參數β相關.
2)噪聲估計區間TN與噪聲的期望λ.由于噪聲具有均勻分布的特性,且在實際環境中目標與成像系統存在一定的距離,故可如(4)式所示,截取中前TN個元素用于估計噪聲的期望λ.TN的選取與目標場景極為相關,一方面可根據系統設計參數或任務要求(如測量范圍)給出合適的值,或可在系統標定校正的時候根據已知場景的強先驗信息給出.
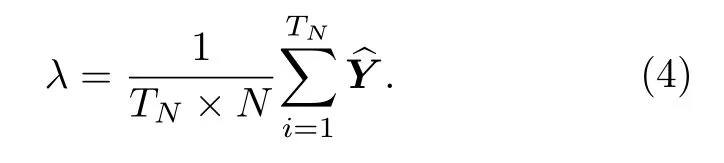
4)平均像素光子數(photon per pixel,PPP)與信號噪聲比(signal to background ratio,SBR).根據(5)式與(1)式可知,PPP 統計回波中信號光子的個數,代表了回波的稀疏程度;而SBR 則通過比例估計了信號與噪聲的差異水平,象征著回波的信噪比.
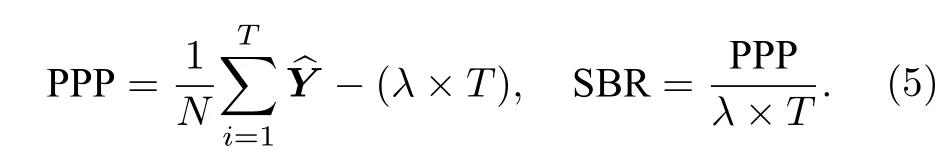
上述特征參數均具有一定的數學或物理意義,因此可以根據系統參數設定或根據回波數據自主獲取,為自適應信息提取奠定了良好的基礎.
2.3 自適應信息提取
本節基于2.1 節中建立的模型與2.2 節設定的參數提出了基于自適應門控的噪聲抑制(adaptive gating based noise reduction,AGNR)算法,通過算法門控的方式自適應地提取目標信息的分布區間.一般情況下,獲取目標信息分布區間的主要瓶頸是強噪聲干擾,因此AGNR 方法從噪聲水平估計與信號模型兩方面入手估計初始門控閾值θ,即有

式中λ×N表示對的每個計時柵格中噪聲期望的估計.根據(1)式與(2)式,可認為縱軸中[λ×N,Λ] 區 間才是信號的分布范圍,且中信號分布的包絡仍具有雙指數分布的性質,即有項;但相比于(3)式,尺度參數β由參數γ替代;位置參數則根據信噪比確定,即采用了 SBR 代替了 |t?α|.(6)式在(3)式的基礎上進一步考慮了特征參數及物理意義,優化了θ的初始估計.


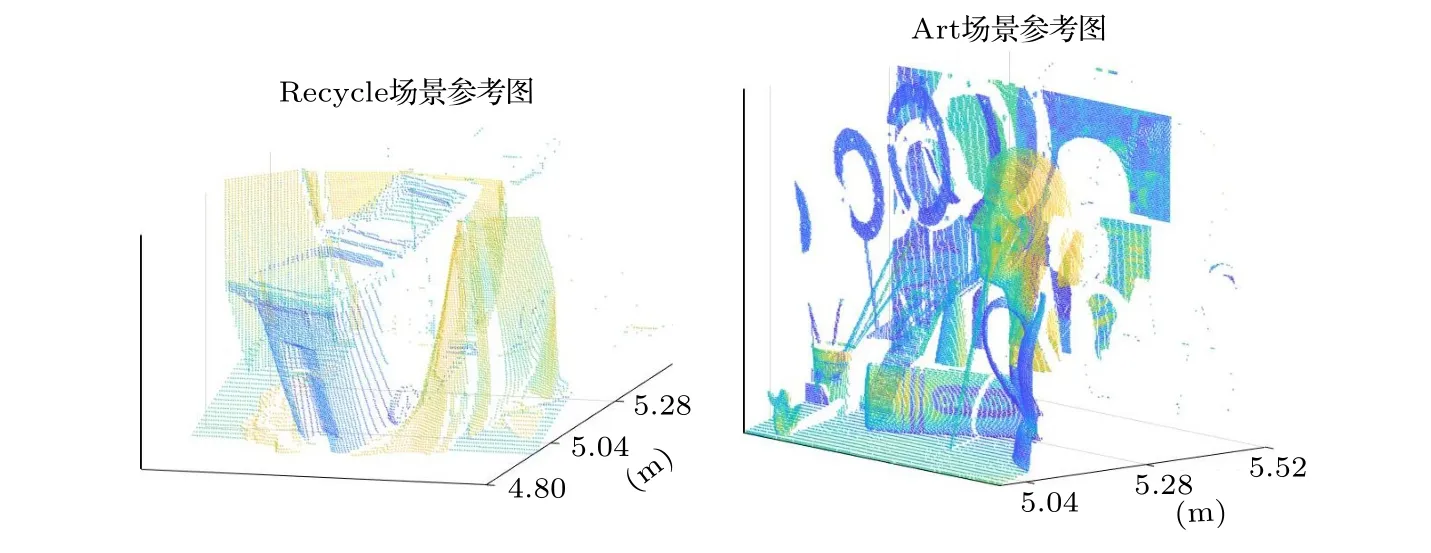
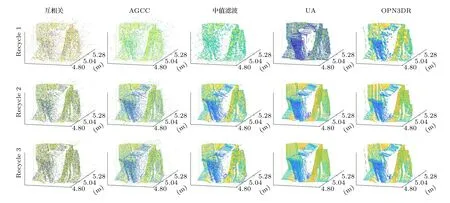
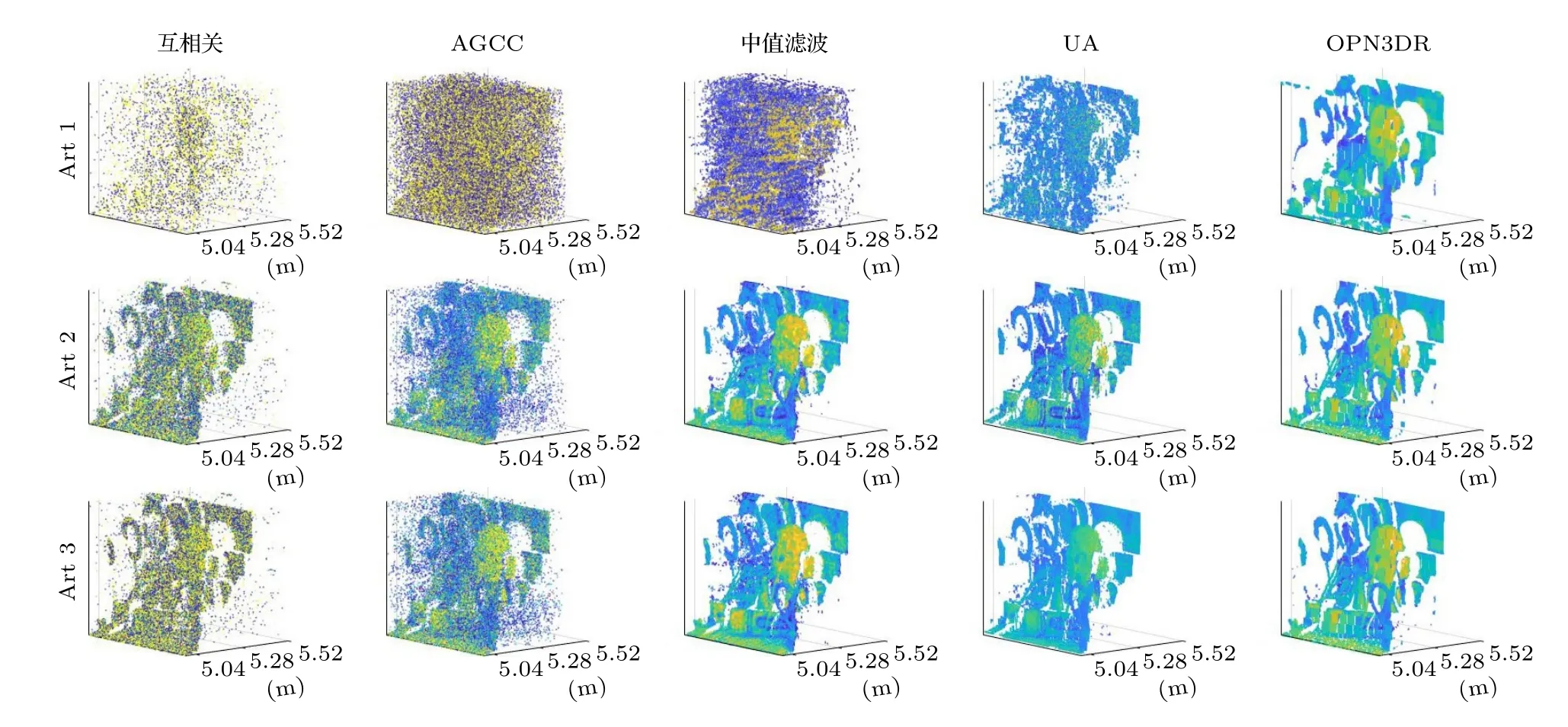
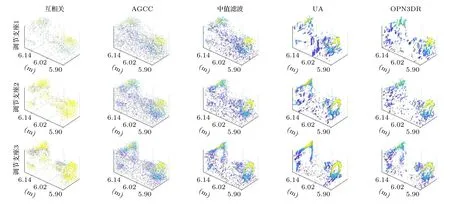
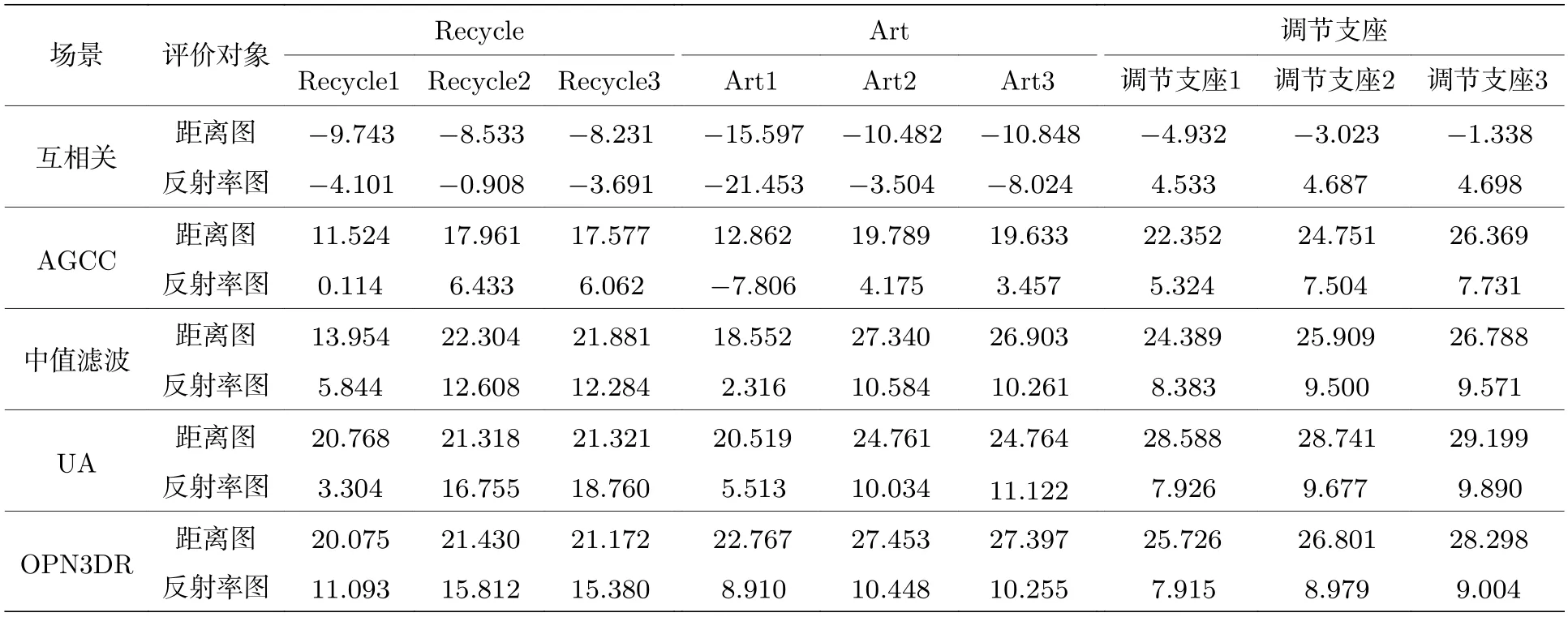
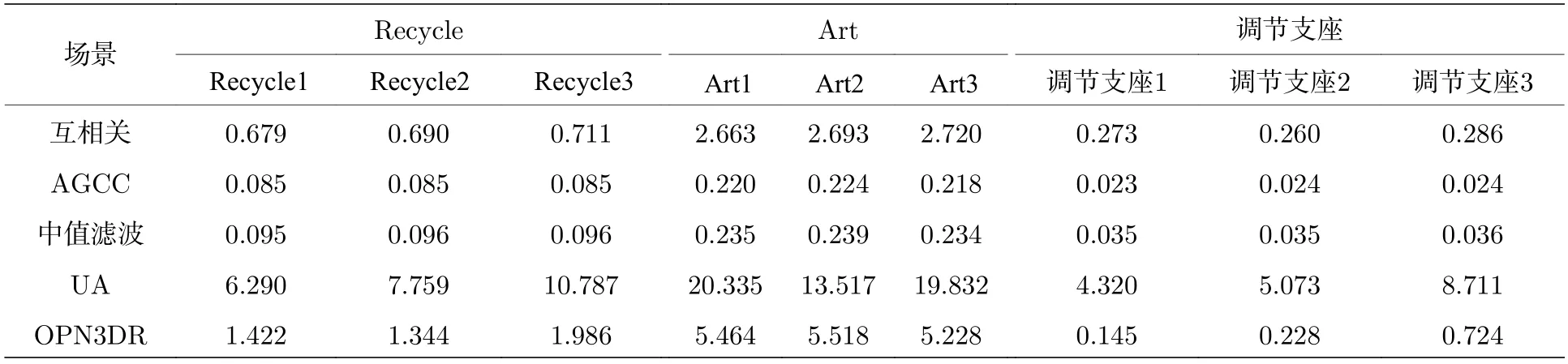
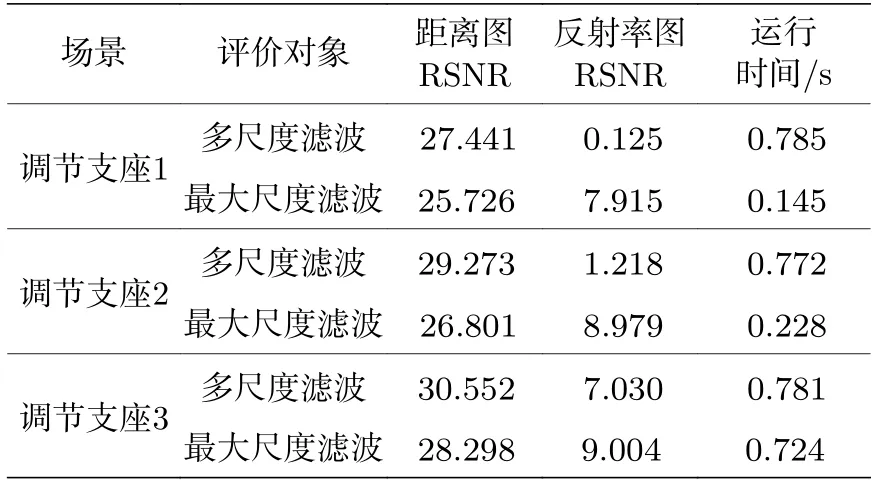
(10)式與高斯分布“ 3σ”法則的形式相近,但積分值為 95% 而非 99.7%.因此本文定義f中(α+3β,α?3β) 區域的寬度為σ,并令ζ={[ζ?σ]∪[ζ+σ},從而以較小的代價增強了信號檢測的能力,(10)式中參數的選取參見(6)式.AGNR 算法的流程見算法1,其中第8 行表示θ1與θ2的獲取過程;第10 行表示若E1 本文提出的AGNR 算法從理論模型出發,在得到門控閾值的初始估計后計算理論計數值與實際計數值的差值,并巧妙地將光子數的差值轉化為對信息提取區間的估計,進而通過迭代逐步確定信息提取區間.最后,根據2.2 節的假設1),本方法濾除了當前信息提取區間內不連續的點和區間以進一步加強抑噪能力,并對區間進行了延拓以加強目標檢測的能力.AGNR 算法實現了與高速電子門控相似的效果,但無需人工預設目標檢測范圍,而是根據數學模型與物理參數自適應地對目標分布區間進行感知與截取,實現了高效且智能的噪聲抑制. 在強衰減、強噪聲等極端的成像環境中,第2 節中介紹的AGNR 算法雖然可以大幅提升信噪比,但由于傳統的圖像重建算法難以克服稀疏與含噪信號重建的問題,因此即使在AGNR 算法的基礎上仍然難以達到較為滿意的成像結果.本文在AGNR 算法的基礎上引入了新型圖像重建算法,通過對回波信號的高效利用進一步提升成像質量,并通過實驗對比分析各算法的性能. 1)互相關算法[17].該方法也稱匹配濾波法,是一種逐點重建算法,也是傳統重建算法的典型代表.令為標定過程中得到的參考信號,yi,j為第(i,j) 個像素的回波,則互相關的結果Ci,j可由(11)式獲得,其中?表示相關操作. Ci,j中峰值在橫軸上的投影即是該像素的距離ti,j;反射率ri,j的估計則由(11)式得出.對所有像素遍歷上述過程即可獲取目標的三維信息. 2)基于自適應門控的互相關(adaptive gating based cross correlation,AGCC)算法.該方法僅對區間ζ內的數據進行處理,即在AGNR 算法的基礎上應用互相關算法.通過與原始的互相關算法對比即可分析AGNR 算法對于重建性能的提升.由于AGNR 算法已經對噪聲水平λ進行了估計,ri,j的估計改由(12)式得出.對于ri,j <0 的像素,均令ri,j=0 以消除無物理意義的反射率值. 與此同時,表5顯示,不同區間范圍內各明細費用對該院費用結構變動的貢獻率是不同的。從總體來看,2012~2016年間引起住院費用結構變動的項目主要有藥品費、手術費、化驗費、檢查費四大項,四者累積貢獻率達69.10%,其中藥品費的結構變動貢獻率高達35.73%,是在各年度中變動最活躍的項目;治療費貢獻率逐年下降,年均減少率為3.74%。具體而言,與2014~2015年相比,2015~2016年間診療費、手術費、護理費、藥品費四項的結構變動貢獻率均有較大幅度增加;床位費、檢查費、化驗費、治療費四項的結構變動貢獻率呈下降趨勢。 3)中值濾波算法.中值濾波是一種典型的圖像去噪算法,本文將其應用于AGCC 算法得到的距離圖t與反射率圖r中,通過圖像處理的手段提升重建質量. 4)解混合算法(unmixing algorithm,UA)[12].該方法被認為是光子計數成像領域中效果最好的圖像重建算法之一.該算法首先通過對三維回波進行降采樣以實現對回波中噪聲信號的抑制,再通過總變分(total variation,TV)正則化方法構建目標函數并求解實現目標信息的三維重建,同時該算法良好的結構也使其具有了并行運算的優點. 5)基于優化的非局部三維重建(optimization based bon-local 3D restoration,OPN3DR)算法[18].該方法通過對回波進行不同尺度的三維低通濾波并融合不同尺度下的信息實現高信噪比的初始估計,再通過非局部重建的思想分析像素間的相關性,并基于此進一步優化成像結果.除此之外,還提出了非均勻采樣算法以降低計算量,從而實現了目標高精度信息的快速獲取,是本領域最新的算法之一.為平衡重建的速率與質量,本文對該方法進行了簡化,僅采用最大尺度進行濾波并得到初始估計,在犧牲少量成像質量的前提下適當加快了重建速率. 為測試本文提出的AGNR 算法的性能,同時分析對比不同重建算法在AGNR 算法的基礎上對成像性能的提升,根據仿真數據與實測數據分別對上述方法展開驗證與分析. 本文基于(1)式與(2)式獲取仿真的回波數據,(2)式中的距離信息t由Middlebury 公開數據集[19,20]中的場景給定,反射率信息r則在原有場景信息的基礎上進行調節以模擬不同的衰減條件與累積時間,λ可人為設定以模擬不同噪聲強度下的回波[21].本文選用了數據集中的Recycle 場景與Art 場景,尺寸Nr×Nc×T分別為96×144×4096與 2 24×256×4096 以仿真較大的目標檢測區間,并參照4.2 節中所述的系統設置物理參數(如計時柵格的寬度設為16 ps).Recycle 場景與Art 場景的參考圖見圖3,其中僅給出了包含目標信息的部分以凸顯目標的細節信息,本文其他章節中的結果也均用該方式展示.為了研究本方法在不同條件下的噪聲抑制能力,Recycle 場景與Art 場景各仿真了3 組回波,其PPP 與SBR 均不相同,具體回波參數見表1. 表1 不同場景下AGNR 算法的抑噪性能對比Table 1.The noise reduction performance of AGNR algorithm under different scenarios. 圖3 仿真場景參考圖.左圖為Recycle 場景參考圖,右圖為Art 場景參考圖Fig.3.The reference image of the simulation scene.The reference image of Recycle scene and Art scene is shown in left and right respectively. 用于數據采集的成像系統原理見圖1,該系統的主要器件型號與參數如下:激光器選用Pico-Quant LDH-D-C-850 型激光器,波段為850 nm,重頻10 MHz,經掃描鏡發射的激光功率約為100 μW;TCSPC 的型號為PicoQuant PicoHarp 300,實驗所用的計時柵格寬度為16 ps.探測器為型號EXCELITAS DTS SPCM-AQRH-16-FC 的SPAD,量子效率可達40%@850 nm,暗計數率<20 cps.接收物鏡型號為KOWA LM25 HC,接收口徑約17.8 mm;帶通濾波片型號為Semrock FF01-850,帶寬為 ± 10 nm.如圖4 中右圖所示,實驗目標為光學系統中常用的調節支座的底部,其外側為圓環狀平面而中心為螺紋孔凹陷,背后則有平板.該場景的參考圖如圖4 中左圖所示,參考圖數據采集于2021 年6 月的夜間,單像素的累積時長為0.5 s,圖像尺寸為 6 4×64×4096.圖4 的左圖僅截取了包含目標信息的部分,由互相關算法直接重建.為營造可控的實驗環境,成像目標與系統均置于遮光布組成的暗室內,因此噪聲水平較低.且在探測器前添加了衰減片以防止探測器被擊穿,參考圖所用衰減片為Thorlab NE10 B-B,實測結果衰減至原信號的16.1%. 圖4 實測場景參考圖及實物圖.左圖為調節支座場景參考圖,右圖為調節支座場景實物圖Fig.4.The reference image and the physical map of the measured scene (i.e.supporting rod scene).The left image is the reference image of the supporting rod scene,and the right image is the physical map of the supporting rod scene. 實驗數據仍由上述系統采集,累積時間同樣為0.5 s,但采集于2021 年6 月的白天,且暗室中一側的遮擋已去除,因此噪聲水平明顯高于參考圖像的采集條件.根據測量結果,暗室內背景光的功率在850 nm 約為1 μW,而發射功率仍為100 μW,經漫反射后回波功率已遠低于背景光的功率.考慮到背景光功率已明顯提升,該實驗在NE10B-B 的基礎上增加了NE30B-B 以保護探測器,組合后實測結果衰減至原信號的0.25%,因此回波相較參考圖也更加稀疏.根據TCSPC 的工作機理,不同累積時間下的回波數據可通過相應軟件從原始數據中提取[3].本文提取了累積時間為5,50 與250 ms的回波數據用于測試,其PPP 與SBR 見表1,其中“調節支座1”、“調節支座2”、“調節支座3”分別對應累積時間為5,50 與250 ms 的回波數據.為方便描述,下文中“調節支座”即對應真實場景圖. 4.3.1 AGNR 算法抑噪性能分析 不同實驗場景的PPP 與SBR 如表1 所列,令SBR′表示經過自適應信息提取后的SBR,并定義噪聲抑制比(noise reduction ratio,NRR)為SBR′與SBR 的比值以衡量噪聲的抑制水平,即有 根據表1 可知,同一場景中NRR 差異較小而不同場景間NRR 差異較大,這主要是因為不同場景之間目標的分布情況差異較大,導致不同場景下區間ζ的寬度Td不同,進而造成了NRR 較大的差異,該結果體現了AGNR 算法對于不同場景的自適應性.但在同一場景中,無論在何種條件下,NRR 均較高且有相近的數值則表明AGNR 算法均能夠穩定地感知并提取目標分布區域的信息.特別是在PPP<1 且SBR<1 的場景(如Recycle1與Art1)中NRR 均可達到較高的值說明該方法具有極端條件下的噪聲抑制能力,取得了與硬件門控相當的效果. 4.3.2 圖像重建算法性能分析 圖5 與圖6 分別給出了第3 節中所述的5 種算法在仿真環境下的重建結果.由于互相關算法直接對含噪的原始回波做處理,且該算法抗噪能力較弱,因此成像效果最差,特別是在回波稀疏且噪聲較強的條件下(如Recycle1 與Art1).AGCC 算法對于噪聲具有一定的抑制效果,例如Recycle1 與Recycle2 中部分受噪聲干擾而不在目標分布范圍內的像素的信息均得到了更優的估計,并且反射率圖(即圖中的顏色)的視覺效果也有了一定的提升;但Art1 場景則顯示在極稀疏且噪聲極強的情況下僅依靠AGCC 算法已不足以完成高質量的重建.中值濾波由于是在AGCC 算法的基礎上進行處理,因此能夠適當提升成像質量,尤其對于Art2與Art3 場景具有較為明顯的效果,但對于極端條件下的重建(如Recycle1 與Art1)仍然難以達到令人滿意的結果.UA 算法相比于前三種方法具有較大的提升,該方法對于所有的場景均能穩定地重建出目標的主要信息,彰顯了其強大的重建能力;但在Recycle1 與Art1 場景中對于反射率的估計偏差相對較大.OPN3DR 算法的效果與UA 類似,對于所有場景的距離信息與反射率信息均有較好的重建能力,但由于該算法對圖像進行了非均勻降采樣,因此圖像存在一定程度的塊效應. 圖5 Recycle 場景重建結果對比圖Fig.5.The comparison of the restoration result of different algorithms under Recycle scene. 圖6 Art 場景重建結果對比圖Fig.6.The comparison of the restoration result of different algorithms under Art scene. 類似地,圖7 給出了上述方法在實測數據上的結果.在三組數據中,互相關算法幾乎無法重建出目標信息,而AGCC 算法雖然有所改善但目標信息仍不夠明晰;中值濾波方法僅在“調節支座3”場景下才能得到較為明顯的目標輪廓.UA 與OPN3DR算法明顯優于前三種方法,在“調節支座2”與“調節支座3”場景中可以獲取較好的目標輪廓,但“調節支座1”的重建結果還不夠理想,這主要是因為圖像尺寸較小,在極端條件下可供分析的數據相對較少. 為了客觀地評價圖5—圖7 中的結果,定義重建信噪比(rconstruction signal-to-noise ratio,SNR)[5]如下: 圖7 調節支座場景重建結果對比圖Fig.7.The comparison of the result of different algorithms under supporting rod scene. 式中 ||·||2表示2-范數,X與分別表示參考圖像與重建圖像,RSNR 的單位為dB. 表2 列出了所有測試場景中距離圖與反射率圖的RSNR.相比于互相關算法,AGCC 算法在所有場景中,對距離圖與反射率圖的RSNR 均有較大的提升,這也體現了表1 中所展示的對SBR 的提升效果.中值濾波的結果也均優于AGCC 算法,且在一些信噪比較高的場景中得到了相對最優的結果,說明了該方法具備一定的抑噪能力,但在極稀疏與極低信噪比的條件下去噪效果不及UA 與OPN3DR.UA 和OPN3DR 算法對于所有場景均能得到較好的RSNR,但二者都存在一定程度的降采樣過程,因此在部分情況下未能得到最高的RSNR.其中UA 在實測數據中均得到了最好的結果,而OPN3DR 算法在Art 場景的距離估計中均獲得了最好的結果,說明UA 在小尺寸圖像的處理方面具有較大的優勢,而OPN3DR 算法能夠更加充分地發掘大尺寸圖像中的信息.UA 算法與OPN-3DR 算法均是在AGNR 算法的基礎上進行處理,通過與AGCC 的對比可以看出兩個算法均優于互相關算法,而通過AGCC 與互相關算法的結果對比則可得到AGNR 算法所起到的關鍵作用. 表2 不同重建算法在不同場景下RSNR 對比(單位:dB)Table 2.The RSNR of different reconstruction algorithms under different scenarios (in dB). 上述算法的運行時間由表3 列出,測試所用計算機的CPU 為i9-10900X,內存為32 G.由于原始回波尺寸較大,因此互相關算法耗時相對較長;而AGCC 算法由于自身具有結構簡單、易于計算的特點,且僅處理有目標信息分布的區域,因此所用時間約為互相關算法的10%,充分體現了本方法的優越性.中值濾波方法所用時間為AGCC 算法耗時與中值濾波算法本身耗時之和,因此略高于AGCC 算法的耗時,但所消耗的時間也遠低于互相關方法所用時間.OPN3DR 算法為了提升成像性能,對回波進行了分析與利用,因此相較于前三者耗時較多,但對于尺寸較小的圖像,其時間成本尚可接受.UA 算法雖然采用了并行計算的方式,但計算復雜度相對較高,因此即使在高性能計算機上也難以實現快速重建的目標.由于OPN3DR 與UA 的結果也是基于AGNR 算法后的信號得到的,因此耗時也是其本身的運行時間與AGNR 算法運行時間之和.而AGCC 算法的時間消耗主要集中于AGNR 算法部分,二者在數值上差異很小,因此本文統一采用AGNR 算法的耗時作為AGCC算法的耗時. 表3 不同重建算法的運行時間(單位:秒)Table 3.The processing time of different reconstruction algorithms (in seconds). 綜上所述,本文提出的AGNR 算法可以大幅抑制回波中的噪聲,取得了與硬件門控類似的抑噪效果,是高質量重建目標信息的關鍵步驟之一.同時該方法還對后續的處理起到了加速的作用.另一方面,圖像重建算法對于圖像質量的提高也起到了較大的作用,其中中值濾波方法抑噪能力有限,適合信噪比相對較高的情況;UA 性能良好但對計算資源要求高,重建速度慢;OPN3DR 相對平衡了重建質量與速率,綜合性能相對最好. 為說明本文采用最大尺度進行濾波得到初始估計的合理性,表4 基于RSNR 和運行時間展示了濾波方式與成像性能對比.通過分析可知采用多尺度濾波可以得到更高質量的距離圖,但由于本文的數據均包含強噪聲,因此在融合不同層級的反射率圖時容易引入噪聲,導致了反射率圖質量的下降.另一方面,由于多尺度濾波涉及多次濾波計算,因此耗時相對較長.綜合來看,多尺度濾波雖然提升了距離圖像的RSNR,但反射率圖像的RSNR下降更多,且耗時相對更長;而“調節支座3”場景中二者的綜合性能相似,考慮到本文主要針對極端條件的成像能力,因此選擇最大尺度濾波的綜合性能更好. 表4 濾波方式與成像性能對比Table 4.The comparison of the performance and the way of filtering. 本文針對光子計數成像技術面臨的強噪聲干擾問題提出了AGNR 算法,該算法可自適應地從回波中感知并提取目標信息分布的區域,從而在大幅提升信噪比的同時保證了較大的目標檢測區間.此外還對圖像重建算法進行了對比分析,其中UA算法與OPN3DR 算法因其充分考慮了圖像的空間聯系,因此對于強衰減強噪聲環境下的重建問題取得了最好的結果.實驗結果表明,在PPP 僅為3.020,SBR 僅為0.106 的條件下,經過AGNR 算法的處理,SBR 相較于原始回波提升了19.330 倍;距離圖的RSNR 相比于互相關算法提升了27.284 dB,在自適應信息提取的基礎上采用OPN3DR 算法與UA 算法后可比互相關算法提升30.658 和33.520 dB.說明在極稀疏且信噪比極低的條件下,本文提出的AGNR 算法是獲取目標高質量三維信息的關鍵步驟,高效的圖像重建算法可在對目標信息分布區間估計的基礎上進一步利用圖像的空間聯系提升重建質量. 本文提出的AGNR 算法不僅兼顧了成像系統的目標檢測能力與噪聲抑制能力,根據成像機理與數學模型實現了對目標信息的自適應感知,還具備計算成本低、運行時間短的特點.因此在未來的實際場景中可與成像系統進行深度融合,在成像過程中實時更新特征參數,以較低的計算成本與時間代價實現對目標分布區間的感知,從而避免人工預設目標檢測范圍,并為后續的圖像重建算法提供有效的先驗信息,推動光子計數激光雷達在復雜環境成像領域的實用化. 感謝中國科學院西安光學精密機械研究所王凱迪博士的討論.
3 圖像重建算法
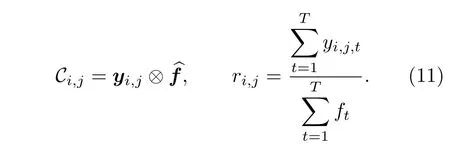
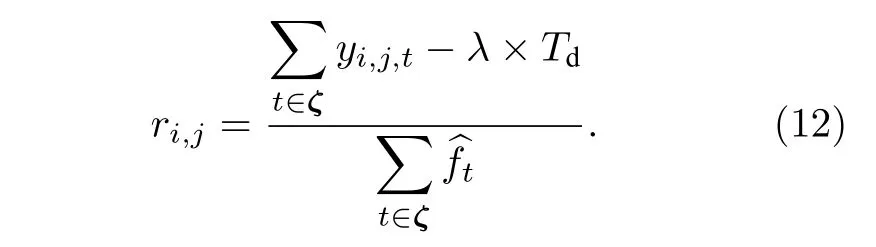
4 實驗結果與分析
4.1 仿真實驗環境

4.2 實測數據獲取

4.3 實驗結果分析
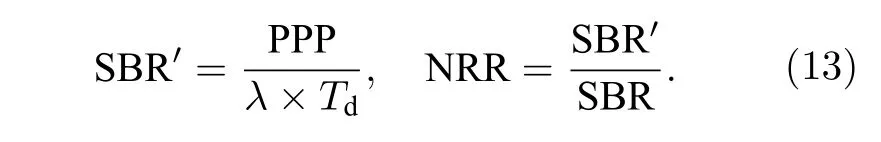
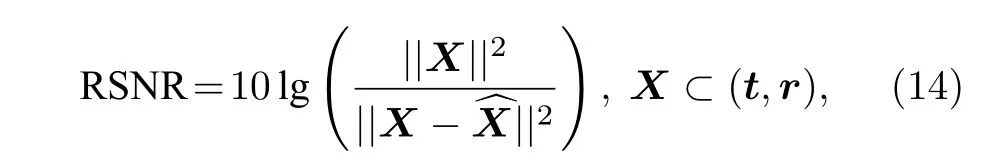
5 結論

