橢圓波束對非均勻手征分層粒子的俘獲特性研究*
白靖 葛城顯 何浪 劉軒 吳振森
1) (西安郵電大學電子工程學院,西安 710121)
2) (中國電子科技集團公司第三十九研究所,西安 710065)
3) (西安電子科技大學物理與光電工程學院,西安 710071)
非均勻手征分層粒子的俘獲特性研究在化學工程、生物醫藥、光鑷、微納米加工等領域都有著重要的應用.為了有效地俘獲及操控手征分層球形粒子,本文對橢圓高斯波束照射下手征分層球形粒子的輻射俘獲力展開研究.從廣義米理論出發,將入射橢圓高斯波束用矢量球諧函數展開,根據波束散射理論及電磁場動量守恒定理,得出橢圓高斯波束對手征分層球形粒子輻射俘獲力的級數表達式,并對橢圓高斯波束入射分層手征細胞時的軸向及橫向俘獲力進行了數值模擬,討論了手征參數、極化狀態、束腰寬度、損耗以及最外層厚度對俘獲情況的影響.研究表明:手征參數的引入會降低非均勻手征粒子的軸向俘獲特性,但是選擇合適的極化態入射時,可以有效地實現對非均勻手征粒子的穩定俘獲.對于內層損耗小的手征多層球形粒子,當內層折射率大于最外層時,最外層厚度大的非均勻手征粒子在光軸上更容易俘獲;反之內層折射率小于最外層時,最外層厚度小的粒子在光軸上有更強的束縛;同時與傳統圓高斯波束相比,橢圓高斯波束的強會聚性更容易實現對非均勻手征分層細胞的三維俘獲,具有良好的應用前景.
1 引言
自從1970 年Ashkin[1,2]報道了激光束對粒子的加速和俘獲以來,光鑷技術就因其可以實現對活體樣品非接觸無損傷的俘獲和操縱,而在物理學、生物學、流體力學等領域引起了廣泛的關注.為了更好地設計光學俘獲系統、理解光鑷技術的物理本質,許多學者對高斯波束照射下均勻球形粒子的輻射俘獲力展開研究,并針對粒子尺寸參數的影響提出了各種不同的計算方法.對于尺寸遠小于入射波長的粒子,瑞利偶極子方法[3]被用來計算作用在粒子上的俘獲力.相反地,幾何光學方法[4]適用于計算粒子尺寸遠大于入射波長的情況.對于尺寸和入射波長相當的粒子,偶極子和幾何光學方法將不再適用.為此,Wu 等[4]、Ren 等[5]與Lock[6]從Maxwell方程的嚴格解析解出發,提出了廣義米理論來研究波束與粒子間的相互作用,并對波形因子的描述給出了詳細的討論[7,8].然而,上述文獻主要研究作用在均勻介質球上的俘獲力,實驗中大多數單核細胞,例如大腸桿菌、紅血細胞、神經細胞和配偶子均可以采用分層球形粒子為模型進行理論分析[9,10],可見對多層球的俘獲力研究在移動、分選及操縱生物大分子上有著深遠影響.許多學者對涂覆多層球的相互作用展開過研究[11?14],Bohren 與Huffman[15]和Kerker[16]最早基于米理論得到了多層球散射系數的解析表達式.Wu 與Wang[17],Li 與Wu[18]分別對多層球散射系數的數值算法提出改進,解決了程序中瑞卡提-貝塞爾函數遞歸引起的誤差.Chen等[19]與Yu[20]等把廣義米理論擴展到波束對多層球的散射研究中并對散射振幅和輻射壓力截面進行了討論.Shore[21]以電磁波理論和微粒極化原理為基礎,分析了任意層數大尺寸粒子的遠場散射特性.汪海賓等[22]討論了不同吸收情況的多層球形粒子在聚焦高斯波束中的聲輻射力影響.然而,以上提到的內容大多只涉及波束與各向同性分層介質球的相互作用研究.
近年來隨著材料技術不斷進步,各種新型電磁介質成為許多學者的研究熱點.手征介質更是憑借其獨特的性能在燃料燃燒、化學工程、遙感通信及生物醫藥等領域[23,24]得到了廣泛的應用.而非均勻手征介質球形微粒的操控特性就是新型手征材料研究的一個重要方向.除了大量基于T 矩陣、矩量法、FDFD 和FDTD 等數值方法研究以外[25?27],解析方法憑借精確解的優勢,使得許多學者對非均勻手征分層球的散射特性開展研究.國外學者較早地開展了有關非均勻手征介質粒子散射的解析理論研究.1993 年,Cooray 與Ciric [28]基于分離變量法推導出分層手征粒子的散射振幅矩陣,數值分析了不同尺寸球粒子的散射特性.1994 年,Ermutlu與Sihvola[25]獲得了雙層手征介質球散射的內場和外場表達式.1999 年,Jaggrad 與Liu [29]建立了瑞卡提矩陣方程來求解多層手征球模型的散射問題.近幾年國內也有學者陸續對非均勻手征介質粒子展開研究.Yan 等[30]研究了高斯波束對涂覆手征介質柱的散射問題,但并未給出散射系數的具體解表達式.Wang 等[31],Gao 與Zhang[32],Zheng 等[33]利用半解析半數值的方法,給出了波束對非均勻手征介質粒子的散射解;李樂偉等[34]提出了研究不連續多層手征介質球的矩陣形式解,然而由于場展開系數用矩陣表示,在大尺寸情況下不方便進行數值計算.為了獲得更直接的表達式,Shang 等[35]研究了在軸入射高斯波束對非均勻手征介質球散射的迭代解析解,并將散射結果擴展到大尺寸手征粒子上.然而,以上提到的內容大多只涉及平面波和圓高斯波束對手征分層粒子的散射特性影響.對于橢圓高斯波束對非均勻手征分層球的俘獲特性研究,文獻很少有提及.
隨著激光探測技術的不斷發展,橢圓高斯波束[36,37]的概念開始在光電測量領域引起了人們極大的興趣,例如在基于柱面波系統進行的探針檢測[38,39]和粒子的虛擬聲速測量[40,41]中,橢圓高斯波束可以克服傳統圓高斯波束對設備引起的誤差和局限,方便測量技術的拓展及應用[42?44].沈建琪等[45,46]詳細討論了橢圓高斯波束對粒子的散射特性,并將橢圓高斯波束的波形因子表達式分別用一維積分簡化和角譜展開方式描述,有效地加快了數值計算速度.李應樂等[47,48]利用Taylor 級數展開方法,研究了橢圓高斯波束對均勻各向同性粒子的散射特性,并提出橢圓波束的腰寬可以有效地改善粒子的識別性能,增強粒子的前后向散射特性.由于對束腰寬度選取的不同,李仁先等[49,50]根據德拜級數的方法,驗證了橢圓高斯波束的強會聚度可以對均勻各向同性多層球形粒子產生很大的俘獲力,從而更容易實現對粒子的捕獲及移動.因此,準確地分析橢圓高斯波束作用在非均勻手征粒子上的俘獲力,將有助于更好地設計光學操縱系統.
本文從廣義米理論出發,對橢圓高斯波束作用下非均勻手征多層球形粒子上的俘獲力展開詳細地討論.將入射橢圓高斯波束用矢量球諧函數展開,研究了手征多層球形粒子對橢圓高斯波束散射的解析解.應用此散射結果,結合電磁場動量守恒定理和麥克斯韋張量積分,推導出橢圓高斯波束對手征多層球粒子的橫向俘獲力及軸向俘獲力的解析表達式,數值分析了手征參數、極化狀態、束腰寬度、損耗及最外層厚度對手征多層球俘獲情況的影響.相關的理論推導均在負時諧因子exp(?iωt)下展開討論.
2 橢圓高斯波束對手征分層球散射的理論分析
圖1 給出了非均勻手征分層介質球對橢圓高斯波束散射的幾何描述,設單色橢圓高斯波束沿z′軸入射,x′軸極化,波束中心的電場幅度為E0,入射波長為λ.橢圓高斯波束在折射率為ng、磁導率為μg的均勻媒質中傳輸,照射到半徑為aj(j=1,2,···,t+1) 的手征分層球上,其中分層區域j內手征介質的介電常數、磁導率、手征參數分別為εj,μj與κj.考慮手征多層球位于坐標系Oxyz下,且球心與坐標原點O重合,設波束中心O′在球坐標系Oxyz下的坐標為 (x0,y0,z0),以波束中心為原點建立與球坐標系Oxyz各軸相互平行的直角坐標系O′x′y′z′,使得橢圓高斯波束的束腰半徑w0x平行于波束極化方向O′x′軸,w0y平行于O′y′軸.
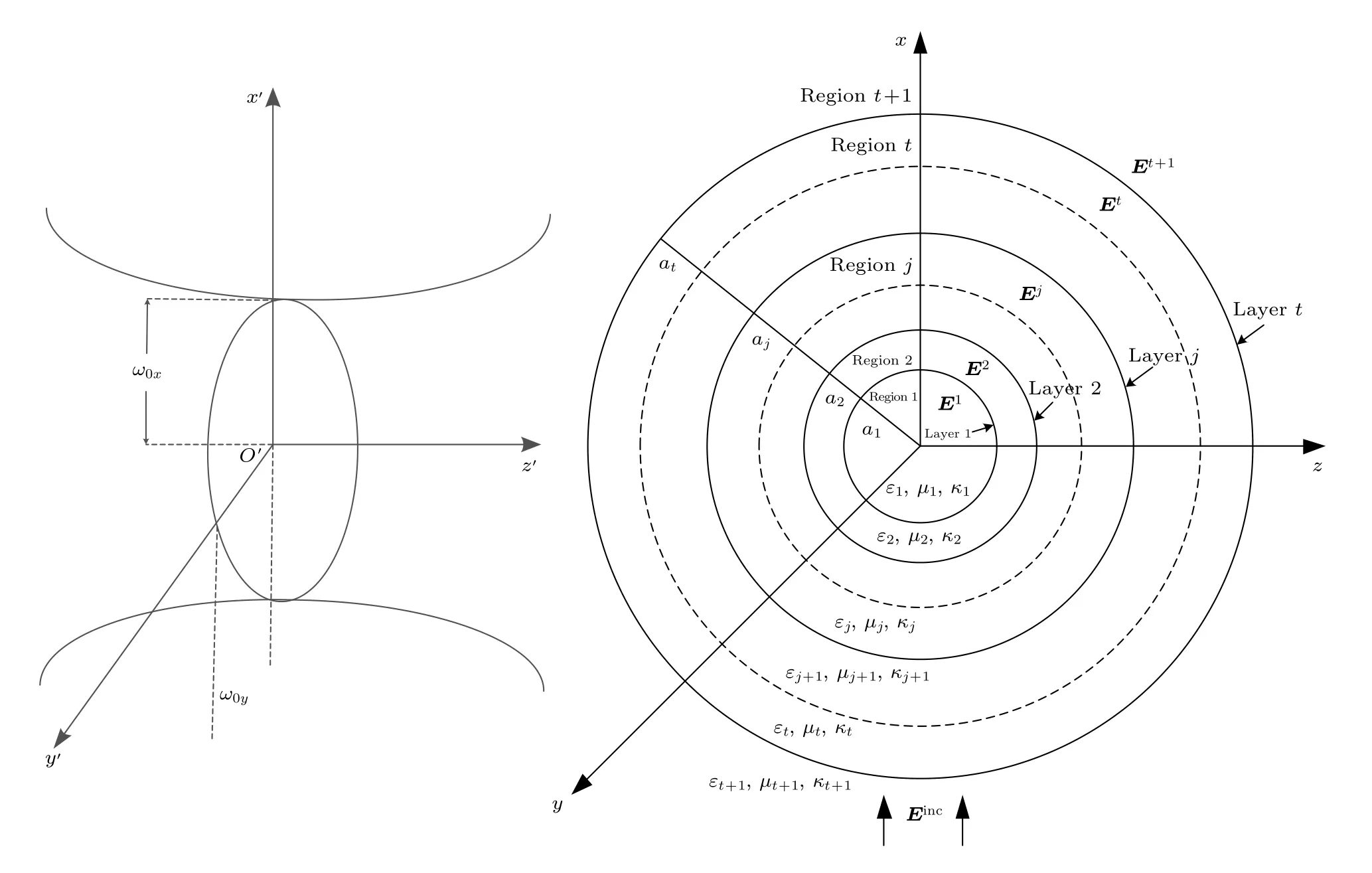
圖1 非均勻手征分層球對橢圓高斯波束散射圖Fig.1.Geometry for scattering of a non-uniform multi-layered chiral sphere induced by laser sheet.
2.1 橢圓高斯波束的展開
一階近似形式下,橢圓高斯波束的電磁場展開式可以表示為

其中E0和H0分別為橢圓高斯波束中心的電磁場幅度;k為橢圓高斯波束在周圍均勻媒質中的波數,一階近似函數可以表示為[36]


根據廣義米理論,以矢量球諧函數的正交完備性為基礎,可以得到入射橢圓高斯波束的一階近似電磁場在坐標系Oxyz下的矢量球諧函數展開式:


2.2 手征分層球的散射理論
將手征分層球的散射場也按矢量球諧函數展開:
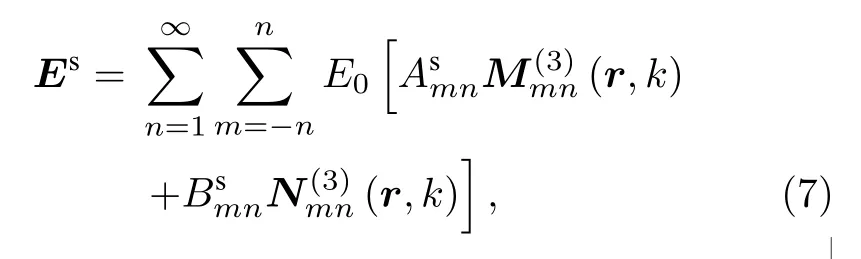




在球外部(區域t+1 中),電磁場表示為入射場和散射場的疊加.入射場展開式選取第一類矢量球諧函數,散射場展開式選取第三類矢量球諧函數.考慮到球外背景介質仍然為手征介質(此目的在于得出背景為手征介質情況下的一般表示方法,當球外背景為各向同性介質時,僅需將背景介質中手征參數退化為κt+1=0,具體形式見后文),區域t+1中的電磁場展開形式如下:






3 橢圓高斯波束對手征分層球形粒子的輻射俘獲力推導
在光鑷系統中會聚到微米量級的激光波束攜帶著很高的能量和動量,經物鏡會聚后的橢圓高斯波束照射到粒子上時,由于光子與粒子的相互作用,使得光束將一部分動量和能量轉移到粒子上,在一段時間內,以粒子受到的輻射俘獲力(梯度力與散射力的合力)表現出來.根據經典電動力學中的電磁場動量守恒定理,波束對被照射粒子的俘獲力等于單位時間內從波束傳遞給粒子的動量,數學上表示為[53]
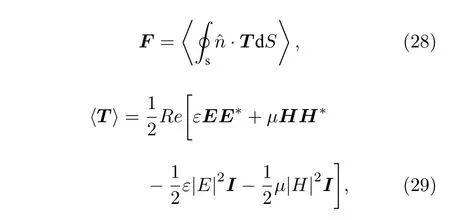
其中ε和μ分別為周圍均勻媒質的介電常數和磁導率;符號 〈〉 代表時間平均;I表示麥克斯韋張量;dS為包圍散射粒子的閉合球面上的面元;n? 為垂直于面元的外向單位矢量;(29)式中的電場E和磁場H均指粒子外部的總場,包括入射場和散射場,即:E=Eip+Es,H=Hip+Hs.
將(29)式代入(28)式,并在大宗量時利用矢量球諧函數的遞推關系和正交關系[54],可以得到手征多層球形粒子在橢圓高斯波束照射下的橫向俘獲力及軸向俘獲力表達式:
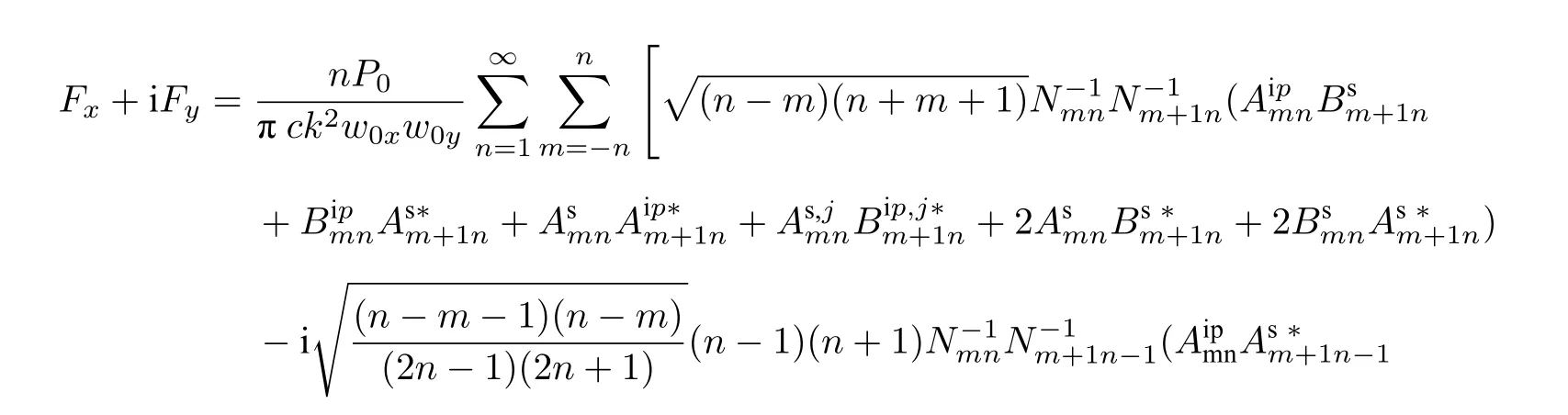
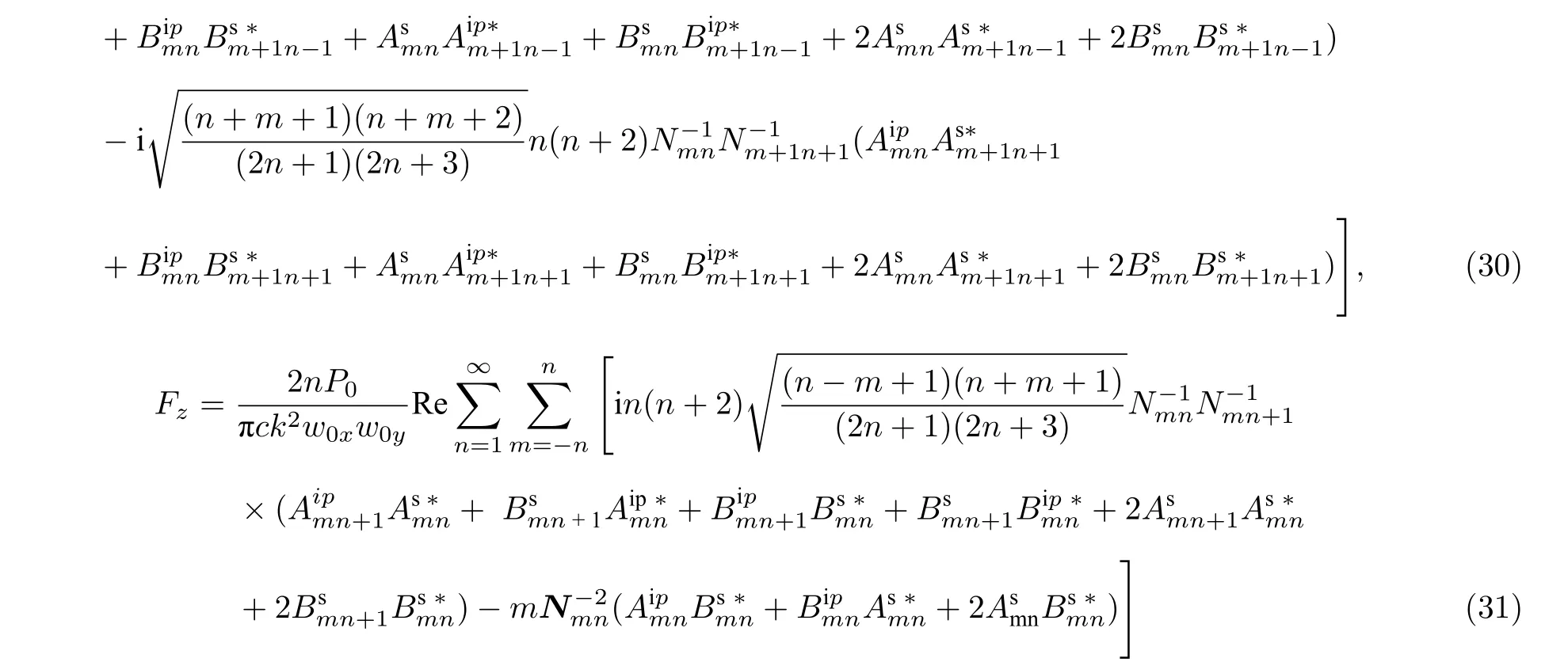

4 數值模擬與結果討論
基于俘獲力的理論表達式,對橢圓高斯波束離軸入射手征多層球粒子時的軸向及橫向俘獲力進行了數值模擬.為驗證本文理論及程序的正確性,取橢圓高斯波束的束腰中心與粒子坐標系Oxyz的原點重合,將離軸入射橢圓高斯波束退化為圓高斯波束,將多層手征介質球(κ=0)退化為非手征各向同性介質球,分別計算其作用在單層球(圖2(a))、雙層球(圖2(b))上的軸向俘獲力及其作用在五層球上的橫向俘獲力截面(圖2(c))隨粒子離軸位置d的變化并與實驗結果及文獻結果進行比較.對于單層球情況,如圖2(a)所示,黑線是本文理論計算軸向俘獲力的結果,“S”和“D”分別為Schut 等[56]給出的靜態和動態實驗測量結果.“Optics”表示文獻[56?58]中有關射線光學的理論結果.其中,橢圓高斯波束的功率P0=100 mW,下面的計算中均取此值.從圖2(a)可以看出,相比于射線光學理論,本文推導的嚴格解析解可以更好地接近實驗結果,特別是軸向俘獲力的峰值與實驗結果非常地吻合.對于雙層球情況,以血紅細胞為例,圖2(b)中線表示本文理論計算軸向俘獲力的結果,點是文獻[9]有關廣義Mie 理論計算的結果.其中,細胞核與細胞質的半徑、折射率分別為:r1=3μm ,r2=3.5μm,n1=(1.3965,0) ,n2=(1.3699,0).從圖2(b)可以看出,當橢圓高斯波束兩個束腰半徑取值相同時,本文退化的結果與文獻結果非常吻合.考慮五層球情況,以淋巴細胞為例,圖2(c)中實線是本文計算橫向俘獲力截面的結果,“Debye”表示文獻[34]有關德拜勢函數的理論結果.其中,淋巴細胞的分層半徑及折射率參數為r1=1.615μm ,r2=2.145μm,r3=2.5μm ,r4=3.085μm ,r5=3.855μm ;n1=1.463 ,n2=1.437 ,n3=1.386 ,n4=1.356 ,n5=1.345.從圖2(c)可以看出,層數發生改變時,本文退化的結果與文獻結果重合地很好,這也進一步驗證了本文理論推導及數值計算的正確性.考慮粒子與光波作用后受到的俘獲力分為兩種:一種是梯度力,是由電磁場對粒子的洛倫茲力引起的,使粒子沿著光場強度的梯度方向運動;另一種是散射力,使粒子沿著光波入射方向運動.利用廣義米理論計算波束作用在粒子上的軸向俘獲力是基于邊界條件進行的,因此是二者的合力.如圖2(b)所示,當橢圓高斯波束w0x=w0y=0.6μm 時,粒子在光軸上束腰中心前方沿光傳播方向運動時,有負的俘獲力出現,此時梯度力大于散射力的作用,粒子將被拉回束腰中心.這是由于小束腰半徑可以形成強聚焦波束,從而實現對光場中粒子的穩定俘獲.隨著束腰半徑的增大,負的俘獲力消失,波束逐漸失去對粒子的俘獲能力.這種現象和均勻介質球被俘獲的現象類似[18].
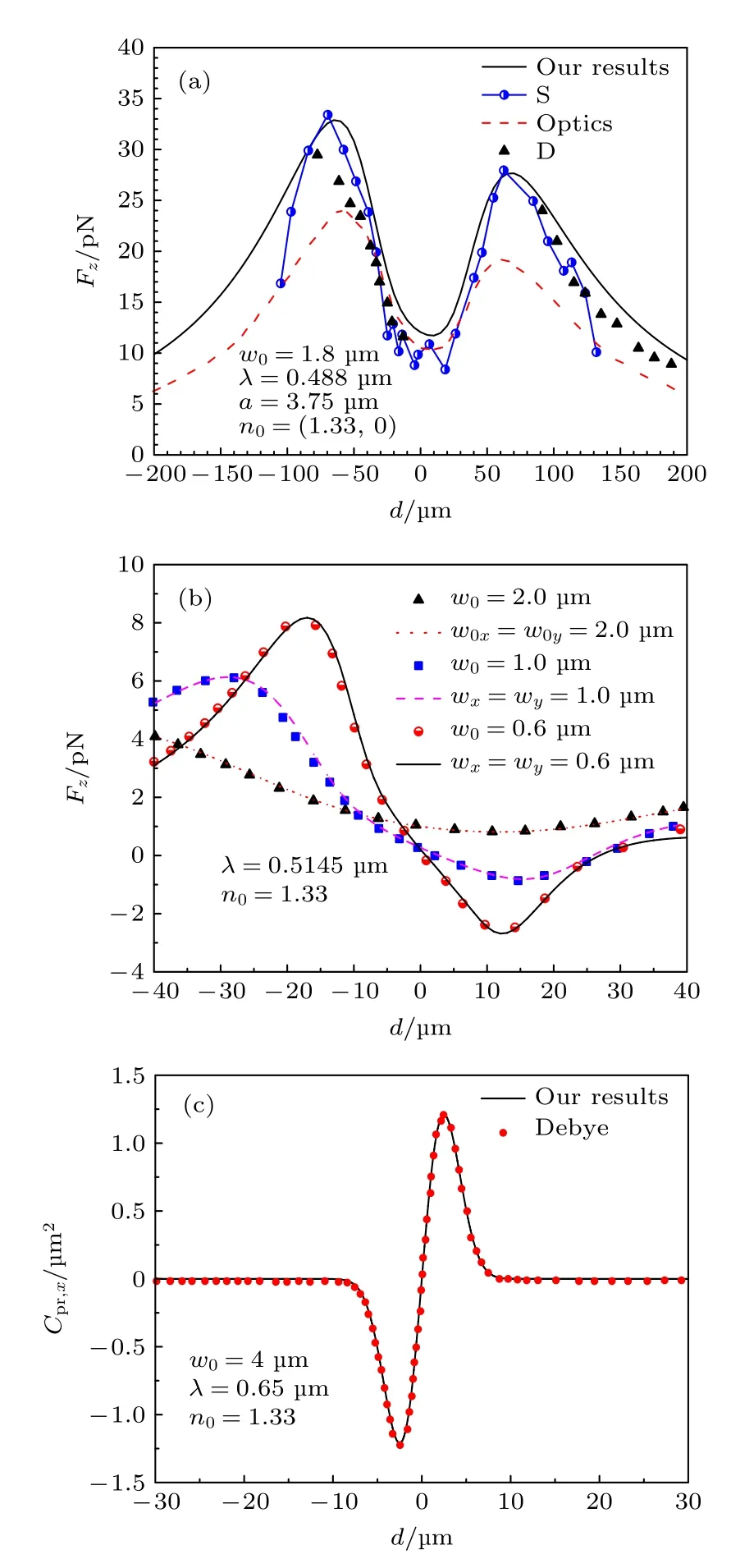
圖2 手征多層球退化為各向同性多層球的輻射俘獲力與實驗及文獻結果進行對比 (a) 單層球對比軸向俘獲力Fz ;(b) 雙層球對比軸向俘獲力 Fz ;(c)五層球對比橫向俘獲力截面Cpr,xFig.2.Comparisons of trapping force (TF) from the theory when multi-layered chiral sphere is degenerated into stratified isotropic sphere with the results from existing references and experiments:(a) Comparisons of axial TF Fz on a single-layered sphere;(b) comparisons of axial TF Fz on a double-layered sphere; (c) comparisons of transverse TF cross section Cpr,x on a five-layered sphere.
圖3 給出不同手征參數下,離軸橢圓高斯波束對雙層手征細胞的軸向俘獲力Fz隨粒子離軸位置d變化的曲線,參照文獻[59]選取雙層手征細胞各部分參數為:r1=1.5μm,r2=3.5μm ,n1=1.39(ε1=1.392ε0,μ1=μ0),n2=1.36 (ε2=1.362ε0,μ2=μ0).背景介質折射率取1.33.激光為x極化橢圓高斯波束,真空中波長取632.8 nm,束腰寬度為w0x=0.6μm,w0y=2μm.雙層球手征參數分四種情況:內核與外層均為非手征介質(κ1=0,κ2=0)、內核與外層分別為手征介質與非手征(κ1=0.5 ,κ2=0)、內核與外層分別為非手征介質與手征介質(κ1=0 ,κ2=0.5)、內核與外層均為手征介 質(κ1=0.5 ,κ2=0.5).入射橢圓高斯波束為x極化波.從圖3 可以發現,四種情況中,內核與外核均為非手征介質球時受到的軸向輻射力最小.此外,內核與外核材質相同時,即均為非手征介質(κ1=0 ,κ2=0)或手征介質(κ1=0.5 ,κ2=0.5)時,軸向輻射力能夠在波束中心附近某一位置范圍內達到負值,即橢圓波束能在此處對手征雙層球實現軸向俘獲.對于另外兩種情況,軸向俘獲力在任何位置都無法實現負值.這說明對于線偏振入射橢圓高斯波束,分層手征參數的引入會減弱波束對手征雙層球的軸向俘獲力特性,使得橢圓波束對非均勻手征粒子的俘獲更加困難.

圖3 不同手征參數對軸向俘獲力 Fz 隨粒子離軸位置d變化的影響Fig.3.Effects of chirality parameter on axial TF with the varying position d of the chiral cell off axis.
圖4 給出不同極化狀態下,離軸橢圓高斯波束對雙層手征細胞的軸向俘獲力Fz隨粒子離軸位置d變化的曲線,球以及波束參數同圖3.圖中雙層手征細胞分兩種情況:內核與外層分別為非手征介質與手征介質(κ1=0 ,κ2=0.5)、內核與外層分別為手征與非手征介質(κ1=0.5 ,κ2=0).入射橢圓高斯波束分別為左旋圓極化(LCP)和右旋圓極化(RCP).從圖4 可以發現,內核為非手征介質,外層為手征介質的時,右旋圓極化的橢圓波束對手征雙層細胞的軸向輻射力遠遠大于左旋圓極化橢圓波束產生的輻射力,并更向束腰中心靠近,使得手征細胞被更快更穩地俘獲在波束中心軸上.因此利用橢圓波束對分層手征細胞球進行軸向俘獲(即實現負軸向輻射力)時,合理地根據粒子的手征參數選擇合適的圓極化入射波,可能更容易實現對非均勻手征介質粒子的軸向俘獲.

圖4 不同極化狀態對軸向俘獲力 Fz 隨粒子離軸位置d變化的影響Fig.4.Effects of polarization states on axial TF with the varying position d of the chiral cell off axis.
圖5 所示為不同束腰半徑的離軸橢圓/圓高斯波束對雙層手征細胞的軸向俘獲力Fz隨粒子離軸位置d變化的對比曲線,圖中波束為右旋圓極化偏振,雙層手征細胞內核與外層分別為非手征介質與手征介質(κ1=0 ,κ2=0.5),其他參數選取同圖3.從圖5 可知,當圓高斯波束的束腰半徑取值為2.0μm時,粒子在光軸上所受的俘獲力恒為正,此時波束在正向光軸上對粒子產生的梯度力小于散射力作用,粒子將遠離束腰中心運動.當入射高斯波束的橫截面由圓形逐漸向橢圓形變化時(即固定圓波束的一個束腰半徑取值不變,改變另一個束腰半徑取值時),由于橢圓高斯波束在空間上具有旋轉對稱性,交換束腰半徑w0x和w0y的取值并不影響在軸橢圓波束對手征細胞的軸向俘獲力,故這里選取w0y不變只討論w0x變化的影響.對于較強會聚的橢圓高斯波束,當w0x≤0.8μm 時,粒子在光束正半軸上將出現負的俘獲力,此時粒子偏離束腰中心時,將受到指向束腰中心的俘獲力被拉回波束中心.這是由于強會聚程度使得波束的能量更集中,從而形成了更大的強度梯度,對粒子產生了更強的軸向俘獲力.隨著束腰半徑的增大,波束會聚程度減弱,軸向俘獲力的最小值在不停的增加.當負的俘獲力消失時,粒子的重力將與正的俘獲力平衡實現粒子的懸浮.此外,可以發現當強會聚的圓高斯波束轉變為橢圓高斯波束入射后,作用在粒子上的軸向俘獲力幅值將出現大幅度的增加.特別是當粒子位于光軸負半軸時,橢圓高斯波束對粒子產生的正向俘獲力將較圓高斯波束有顯著的提高.這是由于橢圓高斯波束在x,y兩個方向上對粒子產生了相對不同的動量改變,當兩側束腰半徑差距越大時,粒子的動量改變越明顯,而物理上波束對粒子照射前后的動量改變決定了波束對其的俘獲力,故橢圓高斯波束產生的軸向俘獲力更強.此時,粒子更容易被橢圓高斯波束俘獲在束腰中心附近.
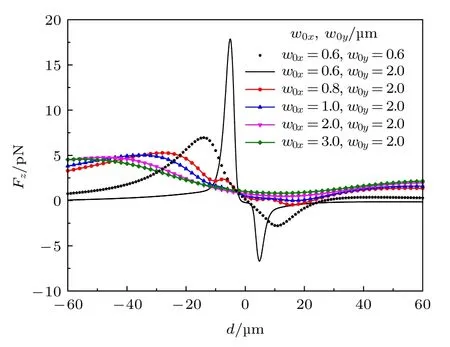
圖5 不同束腰半徑對軸向俘獲力 Fz 隨粒子離軸位置d變化的影響Fig.5.Effects of beam waist widths on axial TF with the varying position d of the chiral cell off axis.
圖6 所示為離軸橢圓/圓高斯波束對不同內層損耗的雙層手征細胞的軸向俘獲力Fz隨粒子離軸位置d變化的對比曲線.其中手征細胞參數為Re(n1)=1.39,n2=(1.36,0),圖中波束為右旋圓極化偏振,其余參數同圖3.由圖6 可知,當粒子內層損耗比較小時,有負的俘獲力出現,粒子將被拉回波束中心.隨著內層損耗增強,粒子在光束正半軸上負的俘獲力開始消失,波束將失去對粒子的束縛,這是由于內層損耗增強,粒子吸收的能量增加,引起散射力遠大于梯度力的影響.對比橢圓高斯波束與圓高斯波束的軸向受力,可以發現當粒子內層損耗相同時,橢圓高斯波束在正向光軸上產生負的俘獲力將更大,且俘獲力取得極值的位置更向束腰中心靠近.這說明相同內層損耗影響下,橢圓高斯波束可以在短時間內產生比圓高斯波束更強的軸向粒子俘獲力,使得粒子更快更穩地俘獲在波束中心軸上.
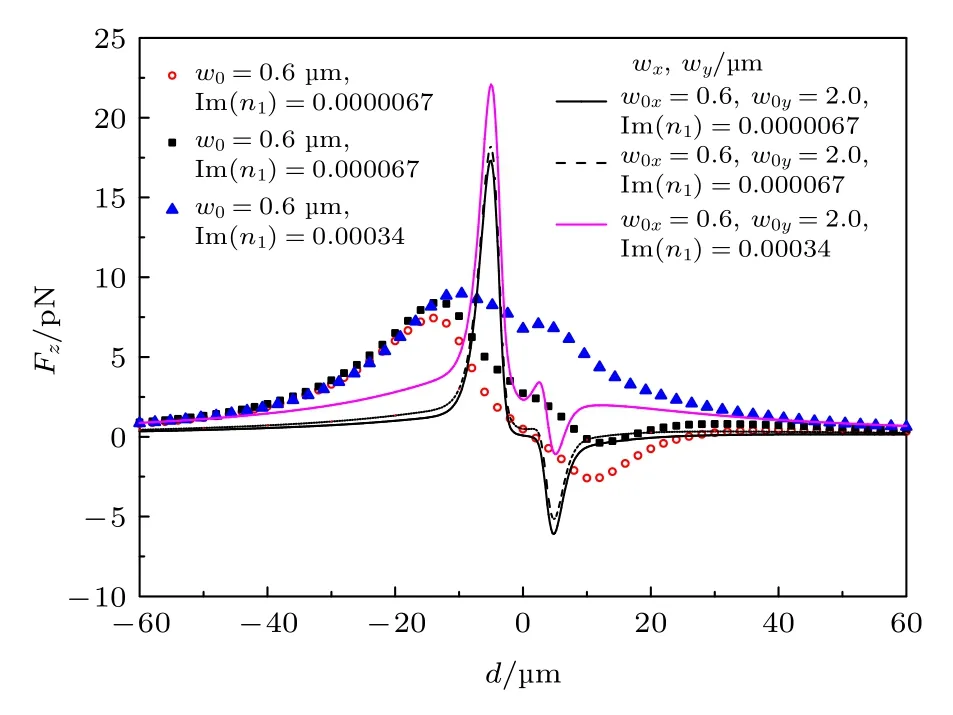
圖6 內層損耗變化對軸向俘獲力 Fz 隨粒子離軸位置d變化的影響Fig.6.Effects of inner material loss on axial TF with the varying position d of the chiral cell off axis.
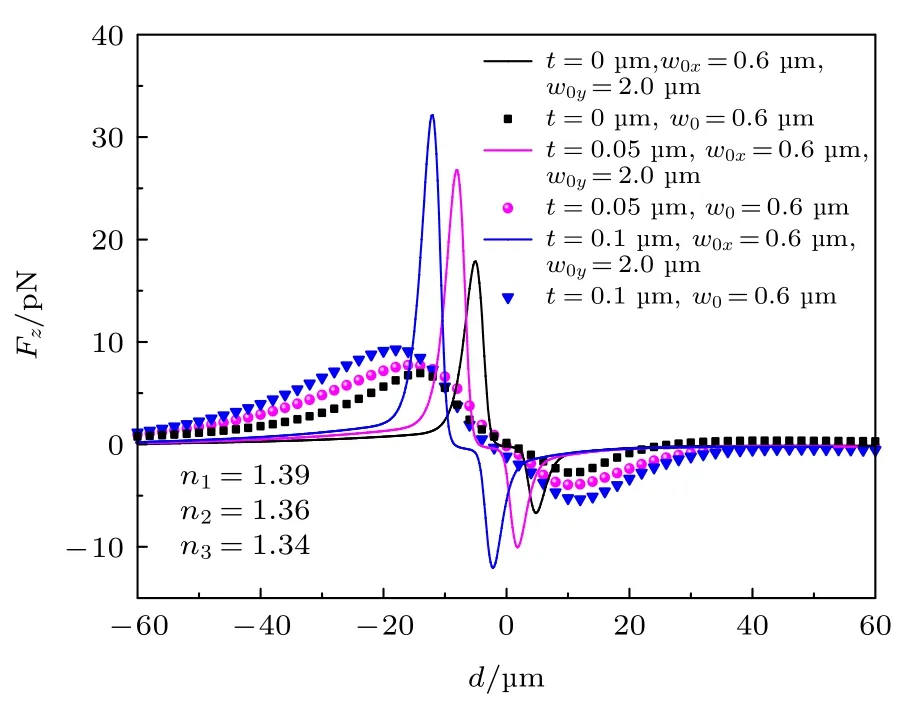
圖7 所示為粒子內層折射率小于外層折射率時,一個三層手征介質球最外層厚度對橢圓/圓高斯波束的軸向俘獲力Fz隨粒子離軸位置d變化曲線的影響.其中,粒子內核半徑r1=1.5μm,折射率為1.39,最外層半徑r2=3.5μm,折射率為1.41,中間層折射率為1.36,中間層半徑分別取3.5,3.45 和3.4 μm,即最外層厚度分別為0,0.05 和0.1 μm;激光為右旋圓偏振波束,真空中波長取632.8 nm,其中圓高斯波束束腰半徑w0=0.6μm,橢圓高斯波束束腰半徑w0x=0.6μm,w0y=2.0μm,背景介質折射率為1.33.手征介質球內核與最外層為手征介質,次外層為非手征介質(κ1=0.05 ,κ2=0 ,κ3=0.05).由圖可知,在最外層厚度t=0 時,橢圓高斯波束的軸向俘獲力在束腰中心附近變化較平坦,但由于周圍液體的外部擾動,粒子不能在這個區域實現固定懸浮.當手征介質球最外層的介質折射率大于內核與次外層折射率時,隨著粒子最外層厚度的不斷減小,俘獲力的極值在不斷地增大,且橢圓高斯波束取得俘獲力的極值一直大于圓高斯波束,并更向束腰中心靠近.特別是當t<0.1μm 時,橢圓高斯波束可以在短時間內更有效地產生比圓高斯波束更強的軸向粒子俘獲力.此外,可以發現當最外層厚度不斷增大時,圓高斯波束在光軸上? 10μm 圖7 最外層厚度變化對軸向俘獲力 Fz 隨粒子離軸位置d 變化的影響(內層及次外層折射率小于最外層時)Fig.7.Effects of outmost particle size on axial TF with the varying position d of the chiral cell off axis (the inner refractive index is less than the outmost refractive index case). 如圖8 所示為粒子內層折射率大于外層折射率時,最外層厚度變化對橢圓/圓高斯波束的軸向俘獲力Fz隨粒子離軸位置d變化曲線的影響,其中,粒子的內層、次外層及最外層折射率分別為n1=1.39 ,n2=1.36 ,n3=1.34,其余參數與圖7 一致.由圖8 可知,當內層與次外層折射率大于最外層時,隨著粒子最外層厚度的不斷增加,橢圓/圓高斯波束的軸向俘獲力極值不斷變大,這與內層及次外層折射率小于外層折射率的情況相反.當粒子在0μm ≤d≤10μm范圍內偏離束腰中心時,都將受到指向波束中心的俘獲力,且力的幅值要大于內層折射率小的情況.可以發現,橢圓高斯波束的軸向俘獲力在過平衡位置時有較大的負斜率,且俘獲力極值大于圓高斯波束,并更向束腰中心靠近,特別是當最外層厚度t>0 時,粒子在短時間內更容易被橢圓高斯波束俘獲在正向光軸上. 圖8 最外層厚度變化對軸向俘獲力 Fz 隨粒子離軸位置d 變化的影響(內層及次外層折射率大于最外層時)Fig.8.Effects of the outmost particle size on axial TF with the varying position d of the chiral cell off axis (the inner refractive index is greater than the outmost refractive index case). 以上討論都是圍繞軸向俘獲力的研究,圖9 給出了單側束腰半徑變化時,離軸橢圓高斯波束對水中手征雙層細胞的橫向俘獲力隨粒子離軸位置d變化的曲線.其中,手征細胞參數取同圖3,當波束中心和球心不重合時,隨著束腰寬度的增加,橫向俘獲力Fx的峰值先增大后減小(如圖9(a)所示),而橫向俘獲力Fy的峰值逐漸增大后保持不變(如圖9(b)所示).這是因為束腰寬度w0x相比于粒子半徑很小時,隨著w0x增加,橢圓高斯波束攜帶的的光子數增多,散射會變大,表現為Fx的峰值增加;但當w0x增大到和粒子半徑相比擬時,橢圓高斯波束在x軸的會聚程度減弱,梯度力變小,表現為Fx的峰值不斷減小.由于束腰寬度w0y固定,橢圓高斯波束在y軸的會聚程度將保持不變.隨著w0x增加,橢圓高斯波束聚集的光子數增多,散射力逐漸變大,Fy的峰值增加.當w0x增大到與粒子半徑接近時,光子數量的增加將失去對y軸散射力的影響,Fy的變化趨勢保持不變.可以發現,盡管橢圓高斯波束的束腰寬度取值不同,手征細胞最終均能在橫向方向被束縛在波束中心上. 圖9 不同束腰半徑對橫向俘獲力隨粒子離軸位置 d 變化的影響 (a) Fx 隨粒子離軸位置 d 變化;(b) Fy 隨粒子離軸位置 d 變化Fig.9.Effects of beam waist width on transverse TF with the varying position d of the chiral cell off axis:(a) Fx changes with the varying position d off axis;(b) Fy changes with the varying position d off axis. 在光鑷技術中經過透鏡高度會聚的激光波束,光場梯度被極大地增強,一定范圍內橫向俘獲力都將把粒子約束在光軸上,實現橢圓高斯波束對粒子的三維操控關鍵在于軸向上對粒子的捕獲;本文從廣義米理論出發,以非均勻分層手征細胞為模型,討論了手征參數、極化狀態、束腰寬度、損耗及最外層厚度對俘獲情況的影響.通過對橢圓波束入射時,軸向俘獲力的數值模擬表明:手征參數的引入會降低非均勻手征粒子的軸向俘獲特性,因此操控非均勻手征粒子要比一般各向同性粒子更加困難.但是不同極化態入射時,非均勻手征粒子的軸向俘獲特性有明顯區別,因此要實現非均勻手征粒子的穩定俘獲,要考慮選擇合適的入射波極化狀態.此外,對粒子的幾何性質及波束參數的數值模擬,可以發現:通過減小橢圓波束的單側束腰寬度將更容易實現對微粒的捕獲和操控.此外減小粒子內層損耗時,橢圓波束對粒子的軸向俘獲能力增強.對于粒子內層及次外層折射率小于最外層折射率時,粒子的軸向束縛隨最外層厚度的減少而變強;反之,對于內層及次外層折射率大于最外層折射率時,粒子的軸向束縛隨著最外層厚度的減少而變弱.在相同數值條件下,橢圓高斯波束可以在短時間內產生比圓高斯波束更強的軸向粒子俘獲力,本文的結論為光鑷技術的改進和實驗測量提供了參考,對多層手征生物細胞的無損檢測研究提供了指導作用.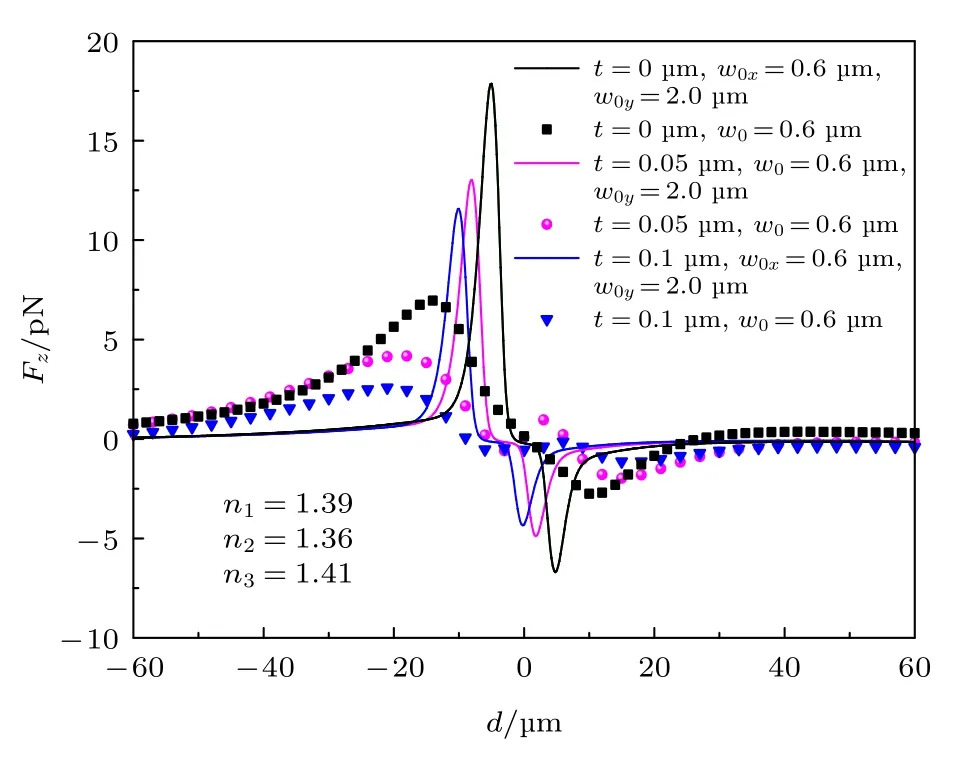

5 結論

