Duffing 振子型結構聲系統中聲能量非互易傳遞的建模和實驗研究*

金江明 謝添偉 程昊 肖岳鵬 D.Michael McFarland 盧奐采?

1) (浙江工業大學機械工程學院,杭州 310014)

2) (浙江工業大學理學院,杭州 310014)

聲能量非互易傳遞機理及聲非互易系統構建是近年來聲學領域的研究熱點.本文開展了由非線性薄膜和兩個不同尺寸聲腔組成的實驗系統中聲能量非互易傳遞的實驗研究.該系統利用簡化為Duffing 振子的薄膜頻響函數的不對稱性,實現了聲能量的非互易傳遞.采用復化平均法獲得系統頻響函數的漸近解,理論計算結果與實驗測量結果吻合.理論計算和實驗結果表明:該系統理論上存在最大9.1 倍的非互易量,實驗測得的最大非互易量為4.3 倍,歸一化跳變區頻率帶寬為0.56.研究結果揭示了實驗系統中聲能量非互易傳遞機理,為實現空氣介質聲系統中聲能量的非對稱傳遞提供了一種新方法.

1 引言

通過在系統中引入具有非線性特性的元件[1,2],實現聲能量的非互易傳遞[3,4],是設計聲二極管[5,6]、聲學斗篷[7,8]、聲單向透鏡[9,10]、隔聲體和拓撲絕緣體[11?16]等新型聲學元件的基礎,是近年來聲學領域[17]的研究熱點.

非線性聲系統具有跳變、隨系統能量變化的共振頻率等線性系統不具有的特性,因而可作為聲能量非互易傳遞的控制元件.按系統非互易產生機理,可分為高次諧波產生[18,19]、分岔[20,21]和非線性共振[22?24]三類非線性聲非互易系統.程建春研究組[18,19]基于非線性介質產生高次諧波產生機理提出了聲二極管,實現了聲能量的單向傳遞.Daraio研究組[20,21]利用一維周期性顆粒鏈結構實現了孤波的整流效應,構建了基于分岔的聲整流器.Vakakis研究組[22?24]利用非線性內共振設計了一系列聲非互易系統.2020 年,汪越勝研究組[25]基于雙原子晶格鏈模型,研究了非線性彈性波超材料的帶隙特性和非互易傳輸特性.近年來,越來越多關于非線性非互易動力系統最新研究成果得到發表.

對于空氣介質聲系統,能量水平低于上述研究中固體、液體介質聲系統3—4 個數量級,同時系統阻尼高、耗散大,缺乏可物理實現的強非線性元件,因此,難以構建空氣介質強非線性實驗系統,至今僅有少數學者開展了相關研究.2010 年,Cochelin 研究組[26]將大振幅非線性振動薄膜與線性聲系統相耦合,構建了非線性能量阱(nonlinear energy sink,NES),實現了聲波的靶向目標能量轉移,并開展了多個類型的NES 系統[27?29]的研究,同時研究了大振幅非線性振動薄膜的寬頻帶吸聲性能[30].這些研究表明利用NES 可以實現聲波的定向傳遞,但對聲波非對稱傳遞還沒有定量的和實驗性的研究.

本文基于Duffing 振子在弱非線性區域的非線性共振和強非線性區的分岔兩種聲能量非互易傳遞機理,構建了由兩個不同尺寸聲腔和簡化為Duffing 振子的薄膜構成的聲非互易實驗系統,并對該系統開展了正反兩個方向上聲能量非互易傳遞問題的建模和實驗研究.首先給出聲非互易實驗系統的設計;然后對非線性聲互易系統的聲腔、薄膜兩類單元進行建模,給出系統理論模型和聲系統的非互易性定義;并對實驗結果與理論結果進行對比分析.

2 聲非互易實驗系統設計

非線性聲非互易系統構成,如圖1 所示.該系統由兩個不同大小的正方體聲腔(邊長分別為0.2 m 和 0.3 m)和一張薄膜組成.不同體積的聲腔使系統具有不對稱性,薄膜的大振幅非線性振動使系統成為強非線性結構聲系統.薄膜固定在分隔兩個空腔的壁面上.薄膜材料為硅膠(polydimethylsiloxane,PDMS),為了獲得具有大非線性的薄膜,在保證薄膜平整、邊界條件均勻的前提下,將薄膜預應力控制到越低越好,本研究中實驗測得的薄膜固有頻率為77 Hz.聲腔材料為PMMA (polymethyl methacrylate,PMMA).

圖1 結構聲非互易系統構成 (a) 實驗系統全貌;(b) 非互易實驗裝置Fig.1.Configuration of the non-reciprocal vibro-acoustic experimental system:(a) The overview of the experimental set-up;(b) the non-reciprocal experimental apparatus.

采用源強可測量的體積速度聲源(型號:Brüel&Kj?r 4295)作為聲系統激勵.采用1/4 inch 傳聲器測量正向、反向激勵下的系統響應,傳聲器安裝在上聲腔和下聲腔的中間位置.采用激光多普勒測振儀(型號:Polytec PSV 400)測量薄膜中心點的振動速度.系統參數和實驗裝置具體參數分別由表1 和表2 給出.

表1 變量和參數表Table 1.Nomenclature.

表2 系統參數Table 2.System parameters.

3 數學模型

3.1 薄 膜

采用Von Karman 非線性板殼模型和Kelvin-Voigt 粘彈性本構模型,由虛功原理,建立薄膜的非線性的運動方程.然后采用拋物線函數作為薄膜一階模態振型函數,通過Rayleigh-Ritz 降階建模方法,獲得簡化為Duffing 振子的薄膜控制方程[22]:

其中ρme為薄膜的密度;υ為薄膜的泊松系數;E為薄膜的楊氏模量;η為薄膜的阻尼系數;h為薄膜的厚度;R為薄膜的半徑;Sme為薄膜的面積;ma為薄膜大振幅運動帶動周邊空氣運動的附加質量,ma值根據實驗結果確定[29];k1和k3分別為薄膜的線性剛度和立方非線性剛度.

3.2 聲 腔

體積速度聲源的輸出可表達為

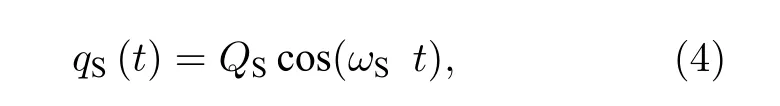
式中,QS為激勵源強幅值;ωS為激勵頻率.

當聲波波長遠大于聲腔尺寸,腔體內不能形成駐波,剛性壁封閉聲腔內的聲壓可認為是均布的.聲腔內聲壓[28]可由下式給出:

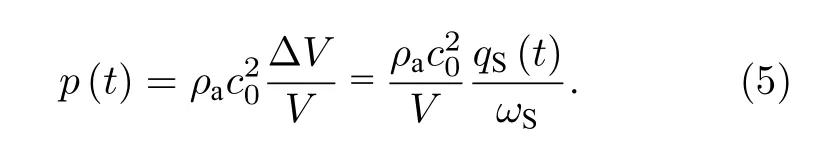
3.3 薄膜控制方程的漸近分析

以薄膜厚度h和線性固有頻率ωm為基準對薄膜控制方程進行歸一化,得到對應的無量綱方程為

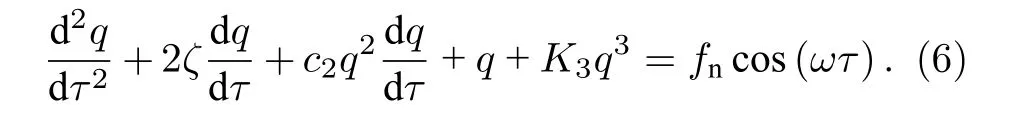
上式中無量綱參數為

采用復化平均法(complexification-averaging method,CX-A) [32],求解頻響函數的漸近解.首先引入:

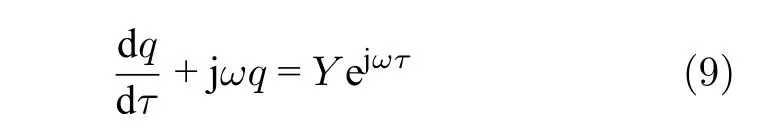
其中Y和 ejωτ分別表示系統響應的慢變分量和快變分量.

通過對快變分量 ejωτ求平均,(6)式可簡化為

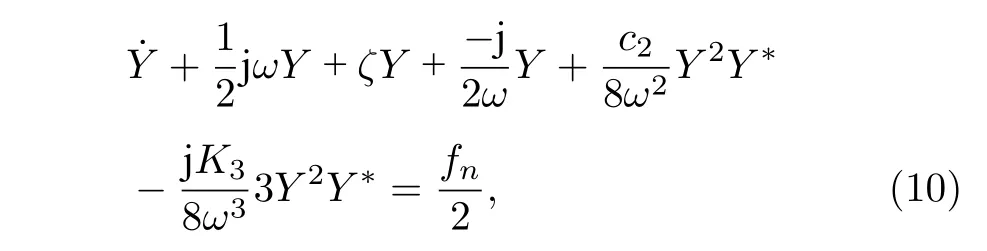
式中,Y*是Y的復共軛.若復振幅Y以極坐標形式表示為

則系統穩態響應有如下特征方程:

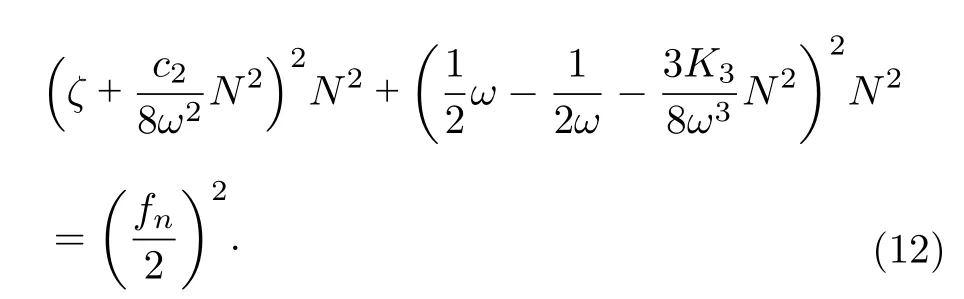
取x=N2,可得到非線性薄膜的頻響函數為:

相對應的背骨曲線公式為

3.4 聲腔響應聲壓及非互易量定義

經Rayleigh-Ritz 簡化,薄膜的平均振動速度與中心點法向振動速度關系可表示為

因此,聲腔響應聲壓可表示為

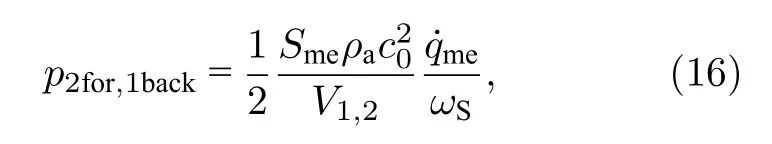
式中,p2for是正向激勵時下聲腔的響應聲壓;p1back是反向激勵時上聲腔的響應聲壓.系統的非互易量NR 可定義為

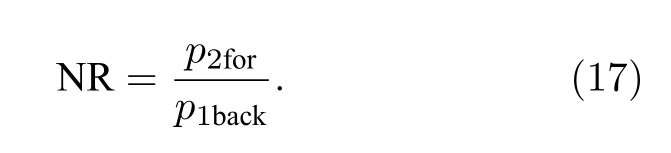
4 理論計算結果與實驗測量結果的對比

薄膜非線性立方剛度的測量實驗系統,如圖2所示.薄膜位移測量采用的是基恩士LK-G 3000激光位移傳感器,量程為–0.1—0.1 m.壓差計型號Extech HD755,量程為2.50 kPa.薄膜一階模態的立方非線性剛度,可以通過多項式擬合實驗測得的薄膜變形與密封腔內壓力變化曲線獲得[33],對于本文采用的100 μm 厚度的PDMS 薄膜,立方非線性剛度k3為3.50×106N/m3.

圖2 薄膜非線性立方剛度測量實驗系統圖Fig.2.Experimental system for measuring nonlinear cubic stiffness of membrane.

實驗中采用體積速度聲源源強為100×10–6m3/s.實驗通過單頻激勵測量聲非互易系統的穩態響應方式進行,測量頻帶范圍為50 至120 Hz,頻率間隔為1 Hz,參考聲壓為 20 μPa.正向激勵時體積速度聲源接入上聲腔中,反向激勵時體積速度聲源輸入下聲腔中.正向激勵和反向激勵下,實驗測得薄膜的頻響曲線如圖3(b)所示.圖3(b)中測量值為由激光多普勒測振儀(Polytec PSV 400)測的薄膜振動平均值,理論值根據非線性薄膜的頻響函數(13)式獲得.

根據頻響函數(13)式和聲腔響應計算(16)式獲得的頻響曲線,如圖3 中的連續曲線所示,其中的計算參數為:ma=1.93×10–5kg,無量綱參數為:ζ=0.019,c2=2.37×10–4,K3=0.0031.

從圖3(b)中可以發現,理論模型計算結果與實驗測量結果基本吻合,說明理論模型和參數準確地描述了實驗系統的動力學響應.在正向激勵下,隨著調節激勵頻率增加,薄膜平均速度從50 Hz 處的0.06 m/s 逐漸增大至91 Hz 處的0.37 m/s,非線性跳變發生在92 Hz.跳變后薄膜平均速度突降至0.09 m/s,跳變后隨著激勵頻率的增大進一步逐漸降低,直至120 Hz 降低到0.02 m/s.

圖3 結構聲非互易系統理論計算與實驗測量結果對比 (a) 激勵聲壓;(b) 薄膜平均速度Fig.3.Comparison of the theoretical and experimental results for non-reciprocal vibro-acoustic system:(a) Excitation sound pressure;(b) average membrane velocity.

由于實驗中存在外界擾動,非線性振動薄膜會從一個分支會突然跳變至另一個分支,越接近理論跳變頻率時越容易發生跳變,因此實驗中沒有獲得臨近理論上的跳變點,即高分支頻率93—99 Hz、低分支89—92 Hz 的實驗數據.

在反向激勵下,隨著調節激勵頻率的降低,薄膜平均速度120 Hz 處的0.008 m/s 逐漸增加至84 Hz 處的0.06 m/s.跳變發生在83 Hz,薄膜平均速度跳躍至0.22 m/s.然后再隨著頻率的降低開始逐漸減少,在50 Hz 處薄膜平均速度降低到0.018 m/s.

在圖3(b)中,108 Hz 處存在小峰值.該頻率是由于體積速度聲源3 m 延長管的一階共振頻率,該峰值由延長管的共振引起.

圖4(a) 給出了正向和反向激勵下響應聲腔內的聲壓,圖4(b)給出了根據聲非互易量計算(17)式獲得的系統的非互易量.圖4(a)測量值是由傳聲器得聲腔內中心點處的聲壓,理論值為由薄膜平均速度(15)式和聲腔響應(16)式計算得.

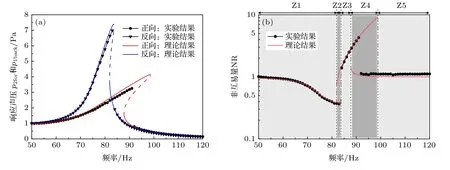
圖4 結構聲非互易系統的系統響應 (a)正向響應聲壓和反向響應聲壓;(b)非互易量Fig.4.Response of non-reciprocal vibro-acoustic system:(a) Forward response sound pressure and backward response sound pressure;(b) non-reciprocal quantity.

從圖4 中可以看出,由于Duffing 振子的頻響曲線在共振區的解不唯一,系統的非互易量曲線可以分為,前跳變區Z1,跳變區域,和后跳變區Z5,其中跳變區又可分為:跳變間隔區Z3,跳變重疊區Z2 和Z4.

在弱非線性的前跳變區Z1,由于薄膜額外存在非線性剛度項,限制了薄膜響應幅值的增加,使得薄膜振幅小于無非線性剛度的等效線性薄膜的響應,薄膜振幅與薄膜激勵聲壓不再成線性比例關系.因此經聲腔體積比例縮放后獲得的系統響應是不同,較高聲壓激勵下的正向響應聲壓小于較低聲壓激勵下的反向響應聲壓,系統非互易量小于1.系統越接近跳變頻率,系統非互易量性越強.

根據背骨曲線(14)式,在非線性跳變頻率處,薄膜振動幅值為

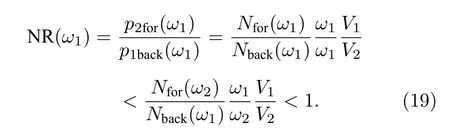
在強非線性的跳變區域,Duffing 振子的頻響函數出現分岔,存在多值解.薄膜頻響函數曲線形成穩定的高分支、低分支及不穩定分支.當系統響應在正向、反向激勵下處于Duffing 振子頻響函數曲線的不同分支,系統存在大的非互易.

在跳變重疊區Z2,正向激勵下Duffing 振子頻響曲線位于高分支.反向激勵下的頻響曲線存在兩個穩態解,由反向激勵下系統初始條件確定.跳變前的非互易量小于1,跳變后,正向響應聲壓大于反向響應聲壓,非互易量大于1.實驗中,在反向激勵下的跳變頻率83 Hz 處之前,非互易量最小值達到了0.37,實驗結果與理論結果相符.

在跳變間隔區Z3,正向激勵下Duffing 振子頻響曲線處于高分支,反向已跳變至低分支,非互易量大于1.

在跳變重疊區Z4,正向激勵下Duffing 振子頻響曲線存在兩個穩態解,由正向激勵的初始條件決定,反向激勵下頻響曲線處于低分支.跳變前Z4 區域的非互易量大于1,跳變后接近1.理論上存在最大9.1 倍的非互易量,由于在實驗中存在干擾,正向激勵下的跳變頻率小于99 Hz 理論值,實驗中跳變頻率為92 Hz,此時系統非互易量為4.3 倍.

在后跳變區Z5,正反向激勵下Duffing 振子頻響曲線都處于低分支.根據頻響函數(13)式,非線性項系數隨激勵頻率增大而快速減小,系統非互易量近似為1.

4.1 輸入能量

圖5 給出了4 個不同激勵源強下系統響應聲壓和系統非互易量的仿真計算結果.從圖5 中可以看到,在1×10–6m3/s 的低源強激勵下,薄膜振動屬于小振幅的近似線性振動,此時,系統是線性互易系統.隨著激勵源強的增加,薄膜振動由小振幅線性振動轉變為大振幅非線性振動,激勵源強越高,薄膜振幅越大,系統非線性越強.對于實驗中采用100×10–6m3/s 源強,薄膜振幅是薄膜厚度的17 倍,系統屬于強非線性系統.

圖5 不同源強輸入下系統響應 (a) 正向響應聲壓(實線)和反向響應聲壓(點劃線);(b) 非互易量Fig.5.System responses under different VVS:(a) Forward response sound pressure (solid line) and backward response sound pressure (dot dash line);(b) non-reciprocal quantity.

隨著系統激勵源強增加,響應聲壓增加,薄膜跳變區變寬,系統最大非互易量的也隨之增加.在高源強激勵下時,線性共振頻率處系統存在一個與激勵源強大小無關的不動點.該不動點數值可根據薄膜頻響函數確定,在線性共振頻率處,頻響函數(13)式可簡化為

從上式可知,系統非互易量的不動點由系統非對稱和立方非線性剛度引起.

其數值為

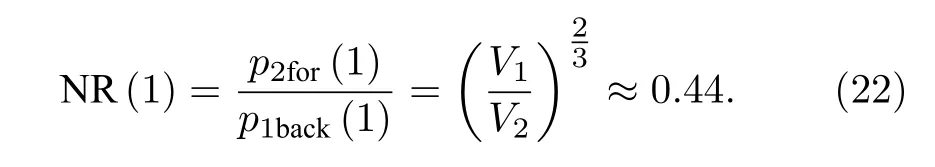
與此相對比的是,與實驗系統相同構型的線性系統在共振頻率處仍是互易的.圖5 中的不動點僅在強非線性聲非互易系統中存在,此現象進一步闡明了系統非線性和不對稱性是聲能量非互易傳遞的必要條件.

4.2 系統不對稱

系統不對稱由兩個聲腔的體積比決定,圖6 給出了聲腔體積比變化對系統非互易的影響的仿真計算結果.圖中,算例1 為實驗系統的聲腔體積比為V1/V2=0.23m3/0.33m3,算例2 體積比為V1/V2=0.253m3/0.33m3,算例3 體積比為V1/V2=0.153m3/0.33m3.以上算例都采用與實驗相同的100×10–6m3/s 源強激勵.

如圖6 所示,反向激勵時,由于激勵聲腔體積相同,聲腔內激勵聲壓幅值相同,薄膜的頻響曲線和跳變頻率不變,此時系統反向響應聲壓與響應聲腔的體積成反比;正向激勵時,由于系統響應聲腔體積相同,系統響應與薄膜振幅成正比.

在前跳變區,正反向激勵下系統響應曲線都處于高分支,在相同源強輸入時,正反向的激勵聲壓與激勵聲腔體積成反比.但由于薄膜控制方程具有立方非線性剛度項和線性剛度項,薄膜響應與激勵聲壓不再是比例關系,薄膜響應幅值的增加比例小于激勵聲壓的增加比例.因此,由正向薄膜響應經系統響應聲腔縮放后獲得的正向系統響應,小于反向激勵下系統響應,系統非互易量小于1.從圖6中也可看出,系統不對稱性越大,非互易性越強.

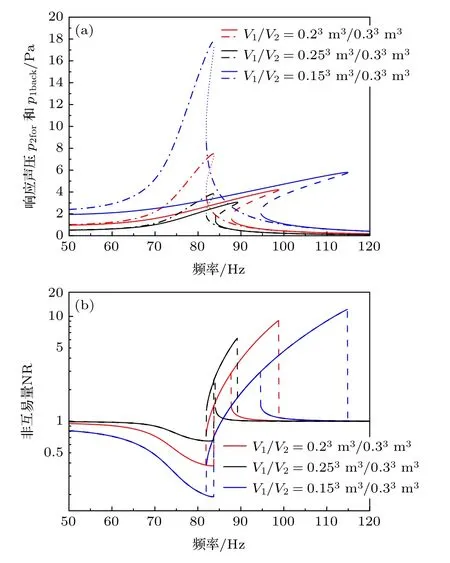
圖6 不同聲腔下系統響應 (a) 正向響應聲壓(實線)和反向響應聲壓(點劃線);(b) 非互易量Fig.6.System responses with different acoustic cavities:(a) Forward response sound pressure (solid line) and backward response sound pressure (dot-dash line);(b) non-reciprocal quantity.

在跳變區,由于系統存在分岔,正向激勵下系統響應曲線處于系統頻響函數的高分支,反向激勵下系統響應曲線處于系統頻響函數的低分支,系統存在大的非互易.隨著系統不對稱性增加,正反向激勵聲壓差異增大,系統頻響函數中兩個分支的區別相應增大,系統非互易量增加,跳變區的頻率帶寬也同步增加.

在后跳變區,正向和反向激勵下系統頻響函數都處于低分支,系統響應幅值幾乎相同,系統可近似認為是互易系統,系統非互易量大小與系統不對稱性無關.

5 結論

為實現研究低能量、高耗散的空氣介質聲系統聲能量的大非互易傳遞,本文基于Duffing 振子在弱非線性區域的非線性共振和強非線性區的分岔兩種聲能量非互易傳遞機理,構建了由兩個不同尺寸聲腔和簡化為Duffing 振子的薄膜構成的聲非互易實驗系統,對該系統正反兩個方向上聲能量非互易傳遞問題進行了建模和實驗研究.

對于系統中大振幅非線性振動的薄膜,采用Von Karman 板殼理論和Rayleigh-Ritz 降階建模方法,將薄膜簡化為具有立方非線性剛度的Duffing振子.由于Duffing 振子頻響函數是非線性的,Duffing 振子響應與激勵不成線性關系,

Duffing 振子響應與激勵大小相反比例縮放后獲得的系統響應是不同的,該系統是聲非互易系統.

采用復化平均法獲得非線性聲非互易系統頻響函數的漸近解,理論計算結果與實驗測量結果相吻合.研究結果表明,該聲實驗系統理論上存在最大9.1 倍的非互易量,實驗中測得的非互易量最大值為4.3 倍,歸一化跳變區頻率帶寬為 0.56.理論模型的參數分析結果表明,隨著輸入能量和系統不對稱性的增加,系統聲非互易幅值和帶寬也隨之增大,同時,在線性固有頻率處系統非互易量不隨輸入能量變化,存在一個由系統非對稱性所確定的不動點.

本文研究結果揭示了非線性剛度和系統不對稱與聲能量非互易傳遞的機理,為聲非互易系統設計提供了一種新方法,在低頻噪聲控制領域有潛在應用價值.