多粒度實值形式概念分析

李金海，鄧小媛，智慧來

(1 昆明理工大學 數據科學研究中心，云南 昆明 650500； 2 昆明理工大學 理學院，云南 昆明 650500； 3 河南理工大學 計算機科學與技術學院，河南 焦作 454000)

形式概念分析提出的本意是希望對哲學上的抽象概念進行數學上的形式化描述與研究，最早從事該研究的是德國數學家Wille教授[1]及其團隊[2]。國內于2000年左右開始關注概念格與關聯規則挖掘等領域的研究[3-5]，主要聚焦國際上比較熱門的基本問題提出新的研究方法。此后10年，國內學者開始對概念格約簡感興趣，給出了各種概念格約簡方法[6-11]。2011年以來，許多學者圍繞決策形式背景上的概念格約簡開展研究[12-17]，這些研究主要基于張文修團隊提出的決策形式背景[18]。與此同時，一些學者又相繼提出了若干新穎的研究課題，比如多粒度形式概念分析[19]、概念認知學習[20-25]、粒描述[26-27]等，這些新興的研究方向大大促進了經典形式概念分析的發展[28]。

一方面，在研究形式概念分析時，實值是描述形式背景的對象與屬性之間關系最為復雜的數據類型之一[29]，它對應的概念格既是區間值概念格的推廣[30-31]，又是模糊概念格的擴展[32-34]，這種推廣或擴展是針對取值范圍的延拓，因其應用廣泛而受到眾多學者的關注[12,14]。此外，實值概念格的并行構造也得到了重視，這類問題主要側重快速計算概念節點[35]。另一方面，粒計算與形式概念分析的結合日漸深入，從最早的粒概念及其約簡開始[8]，到隨后的概念知識粒與概念信息粒[36]，以及近期開展的一系列跨領域、深層次、多角度的融合研究，充分表明這兩個理論有非常好的結合性[37-38]。特別地，自從將粒計算中的多粒度思想[39-40]引入形式概念分析后，很快建立了多粒度形式概念分析理論[41-43]，并成為熱門研究話題[44-45]。為了進一步拓寬實值概念格的應用范圍，還需繼續研究多粒度實值形式概念分析，即如何借助多粒度思想探討實值概念知識發現與規則提取。

鑒于上述分析，本文基于多粒度數據或多粒度關系提出多粒度實值形式概念分析方法，旨在探究多粒度概念知識空間的概念轉移規律以及規則推理的運算關系，具體提出了實值類屬性塊以及多粒度實值形式背景，給出了帶決策的多粒度實值形式背景的知識發現方法，為今后多粒度實值數據的多層次知識發現研究奠定了理論基礎。

1 實值形式背景與實值概念

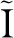
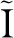
(1)

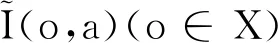
Δ(A)=

是實值屬性集A上的所有實集構成的集合，其中μt(ai)(i=1,2,…,m)是實區間集。算子↑:2U→Δ(A)和↓:Δ(A)→2U定義為

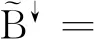
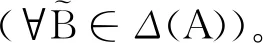
(2)

從(2)式可以看出，

(3)

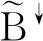
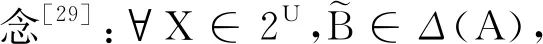
2 多粒度實值形式背景

前文討論了實值形式背景和實值概念，下面再將多粒度思想引入實值形式背景中，提出多粒度實值形式背景。為此，約定來源于同一類別(類型)的實值屬性構成的集合稱為實值類屬性塊。

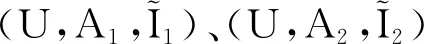
(4)

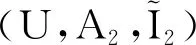
需要指出的是，本文提到的粒度粗細均包含了粒度相等的情況。

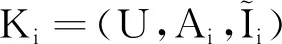
實際上，多粒度實值形式背景刻畫了實區間集賦值之間的一種關系。具體地，對于描述一個對象的問題，可以選擇在粒度粗的屬性下進行統一的籠統描述，也可以選擇在粒度細的多個分屬性下進行具體的描述。當然，在不同的粒度空間下描述對象，其提供的信息是不等價的，細粒度空間中的描述通常比粗粒度空間中的描述給出了更多可供參考的信息。

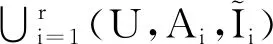
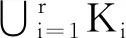
(5)

根據假設，{as}s∈S、{bt}t∈T均為布爾屬性集，且{as}s∈S和{bt}t∈T擁有的對象形成論域U的劃分。那么對于任意對象o∈U，由公式(4)可得fo(ai)=fo(bj1)∪fo(bj2)∪…∪fo(bjk)成立。因此，當fo(ai)=?時，fo(bjt)(t=1,2,…,k)均為?；當fo(ai)={1}時，fo(bjt)(t=1,2,…,k)中有一個為

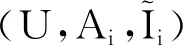
性質1表明多粒度實值形式背景是經典多粒度形式背景的推廣。為了敘述方便，本文討論的多粒度實值形式背景均默認形成特化全序關系，即實值類屬性塊的粒度越來越細；另外，最粗的實值類屬性塊的元素個數均設為1，這是出于畫粒度樹的需要。

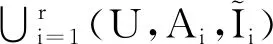
由于前面已約定最粗的實值類屬性塊的元素個數均為1，那么粒度樹的根節點通常只有一個。此外，根據定義5，來自同一粒度空間的屬性要求排在同一層，那么每棵粒度樹的總層數均為r，即與多粒度實值形式背景的粒度層數相同。

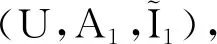
表1 實值形式背景

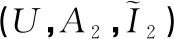
表2 實值形式背景

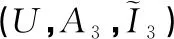
表3 實值形式背景

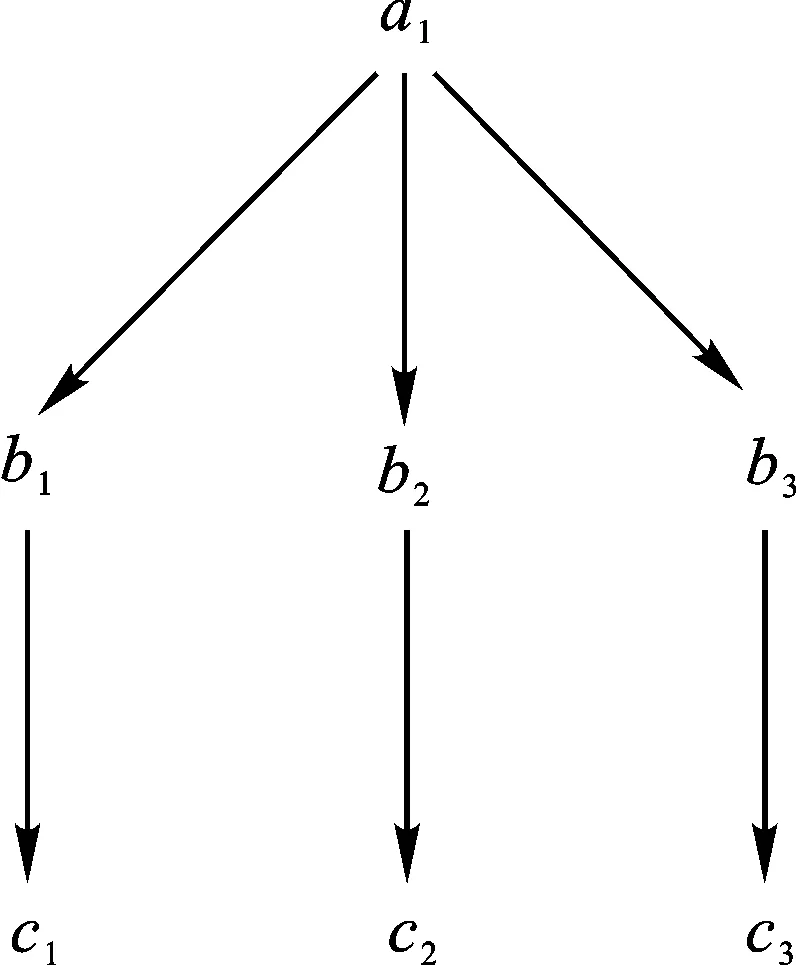
圖1 屬性a1的粒度樹Ta1

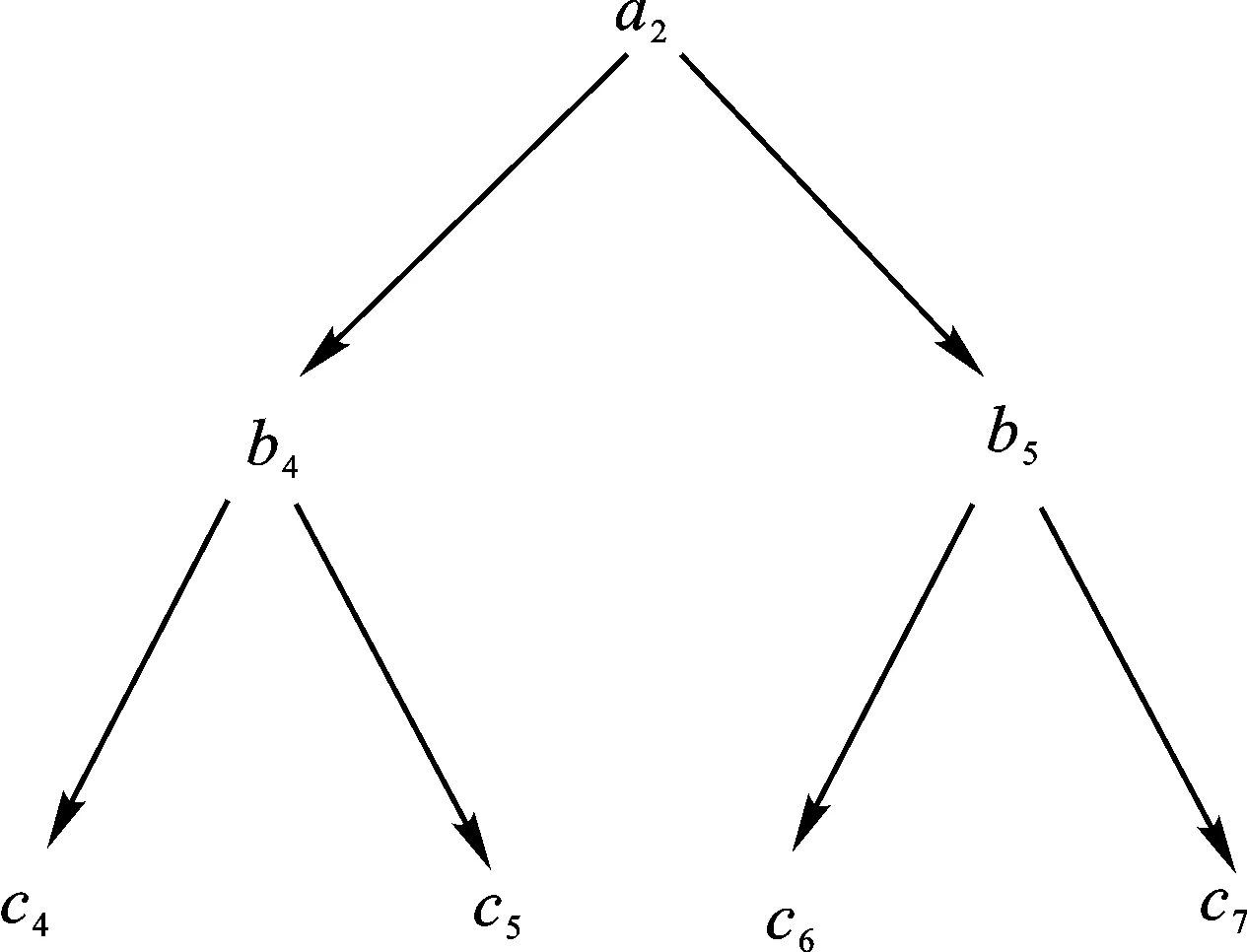
圖2 屬性a2的粒度樹Ta2

容易驗證，對表1～3的實值形式背景并置形成一個多粒度實值形式背景。具體地，由圖1可知表1的類屬性塊{a1}比表2的類屬性塊{b1,b2,b3}粒度粗，表2的類屬性塊{b1,b2,b3}與表3的類屬性塊{c1,c2,c3}粒度粗細相同；由圖2可知表1的類屬性塊{a2}比表2的類屬性塊{b4,b5}粒度粗，表2的類屬性塊{b4,b5}又比表3的類屬性塊{c4,c5,c6,c7}粒度粗。

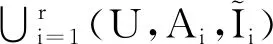
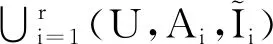
證明設粗粒度實值形式背景的L-實概念的外延為X。一方面，在細粒度實值形式背景中X的每個對象仍屬于X對應的誘導L-實概念(X↑↓,X↑)；另一方面，對于任意對象o∈U-X，它肯定不屬于X對應的誘導L-實概念(X↑↓,X↑)，否則可以推出對象o在粗粒度實值形式背景中也屬于外延X，這與X是L-實概念的外延矛盾。綜上可知，X=X↑↓，即X在細粒度實值形式背景中也是某一L-實概念的外延。

性質2表明，在多粒度實值形式背景中，細粒度實值形式背景的L-實概念的個數比粗粒度實值形式背景的L-實概念的個數多，這是因為在粗粒度實值形式背景中滿足“主要小于”關系的對象在細粒度實值形式背景中可以不滿足“主要小于”關系。即在粗粒度實值形式背景下不能形成L-實概念的序對在細粒度實值形式背景中有可能形成L-實概念。

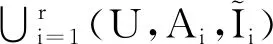
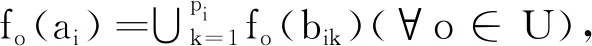
即對于粗粒度實值形式背景的L-實概念，它的每個實值屬性ai的可能取值是細粒度實值形式背景中對應的特化屬性可能取值的并。

性質3表明，多粒度實值形式背景的各個單粒度實值形式背景的L-實概念之間可以相互轉化，即可以由粗粒度空間中的L-實概念拆分得到細粒度層的L-實概念，也可以由細粒度空間中的L-實概念合并得到粗粒度空間的L-實概念。依據上述性質，下面給出一個由細粒度實值形式背景的L-實概念得到粗粒度實值形式背景的L-實概念的算法。

算法1 計算粗粒度實值形式背景的L-實概念

輸出：粗粒度實值形式背景的L-實概念Q。

初始化Q=?；

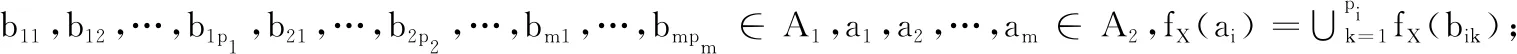
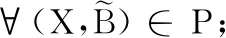
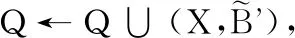
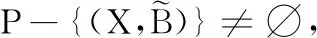
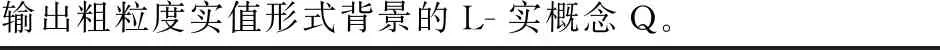
輸出粗粒度實值形式背景的L-實概念Q。

例2對于例1中的多粒度實值形式背景，第1和第2粒度層下的實值形式背景的概念格分別如圖3和圖4所示，其中節點的詳細信息見表4和表5。

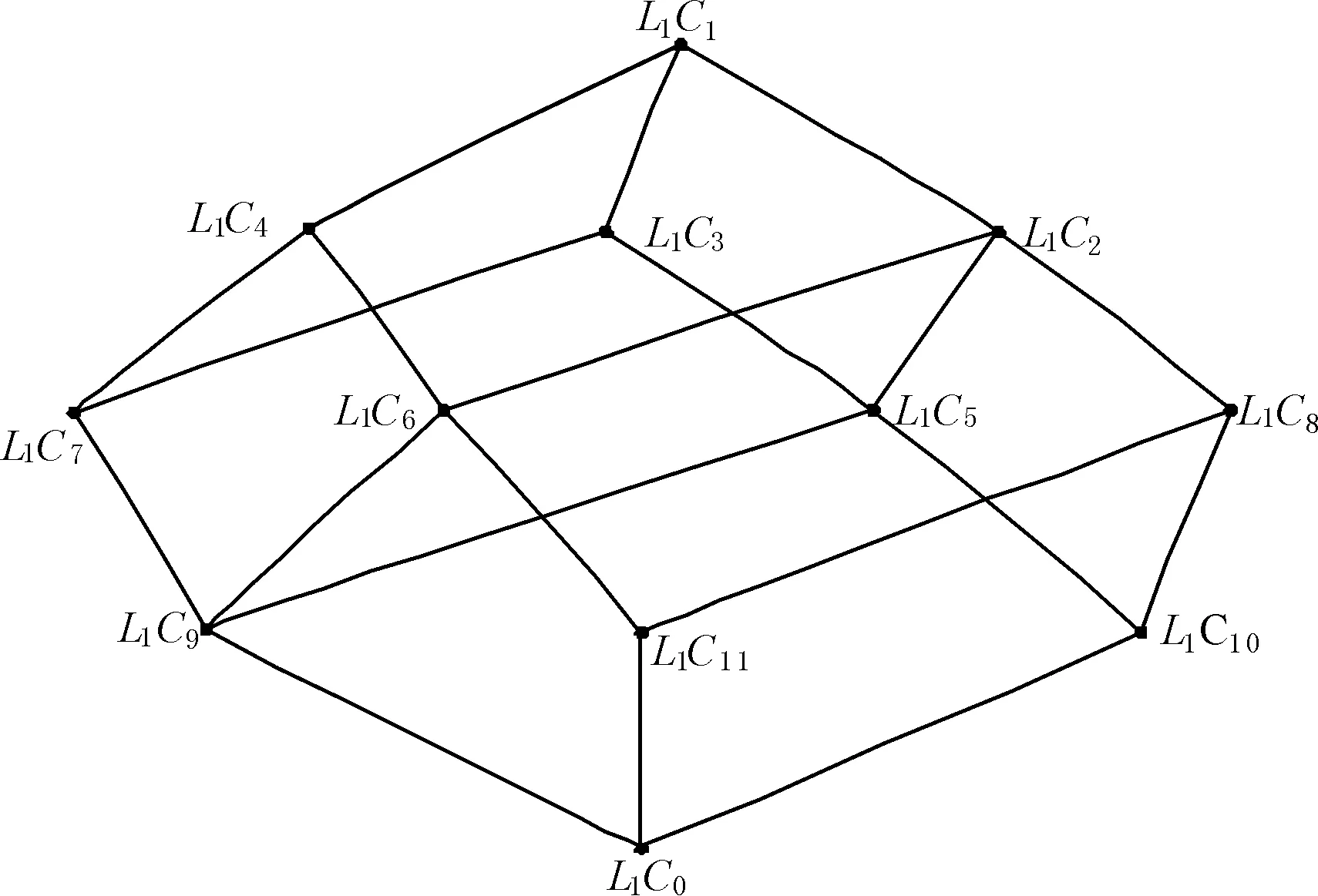
圖3 表1的實值形式背景的概念格

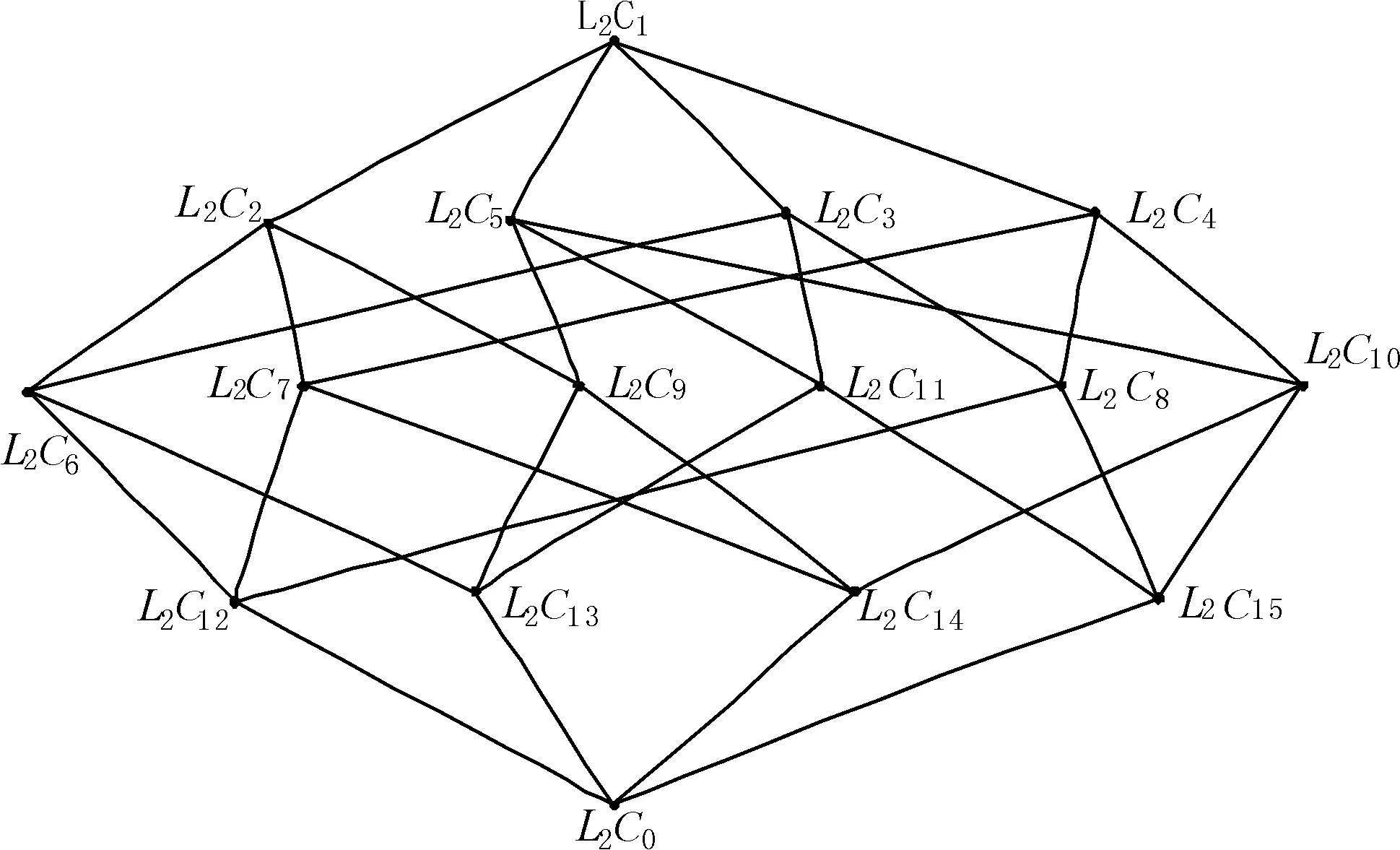
圖4 表2的實值形式背景的概念格

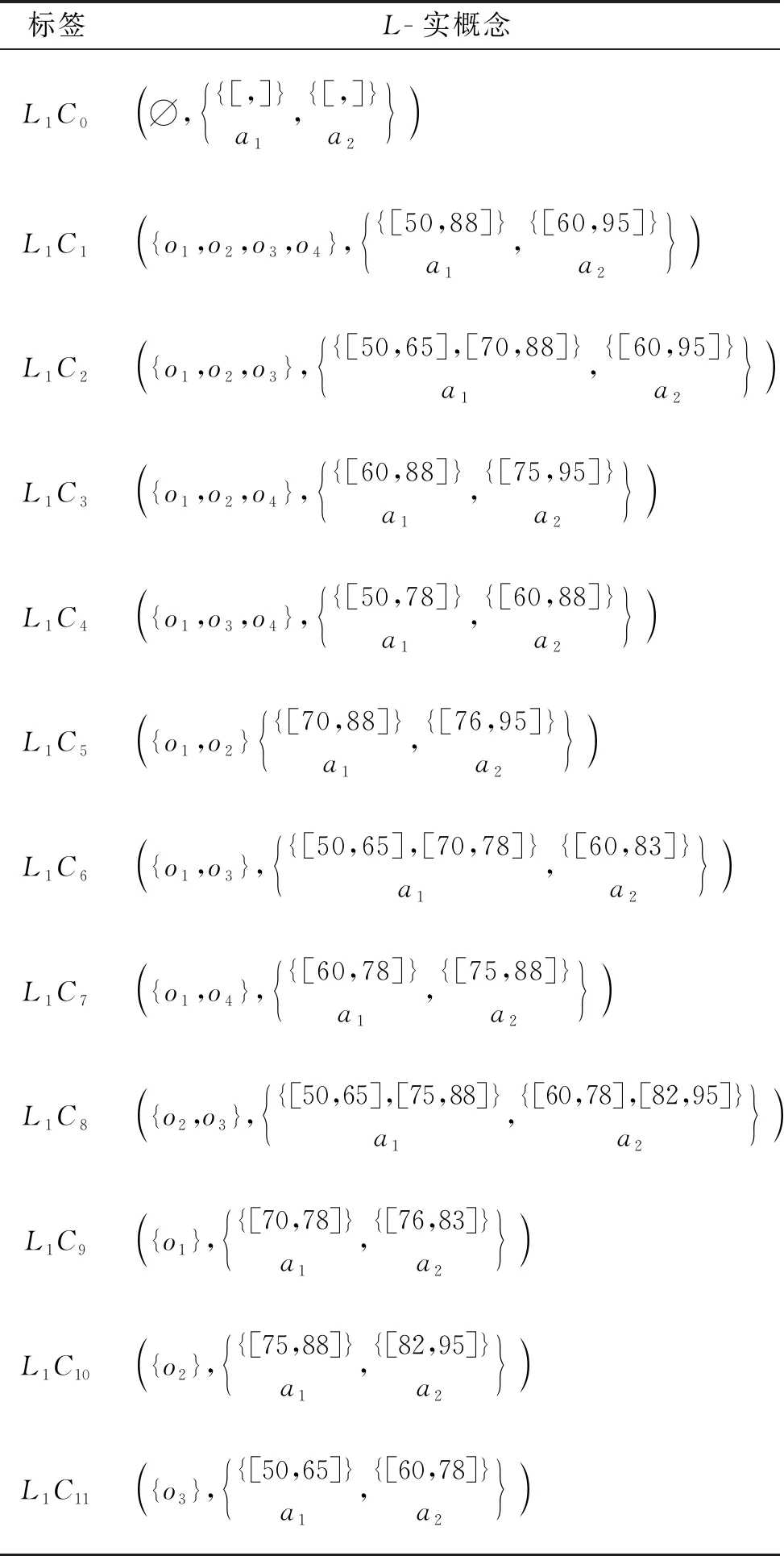
表4 表1的所有L-實概念

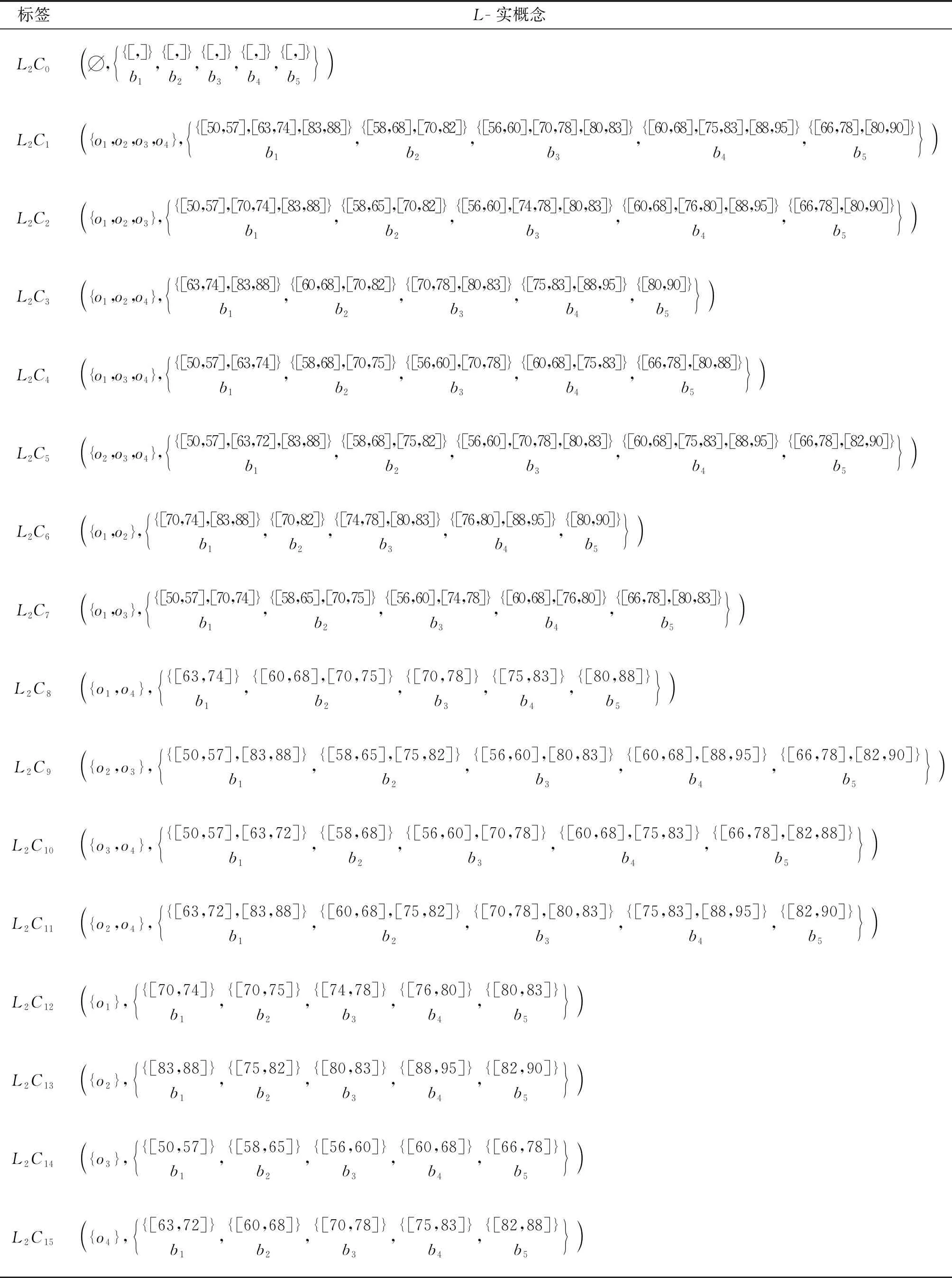
表5 表2的所有L-實概念

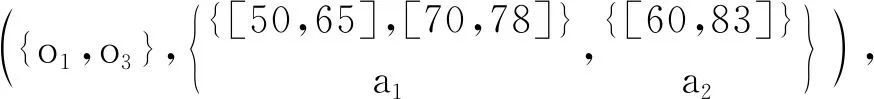
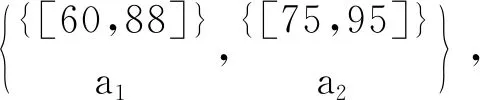
3 多粒度實值決策形式背景的知識發現

本節進一步將決策屬性引入多粒度實值形式背景中，討論多粒度實值決策形式背景各粒度層下決策規則之間的聯系。

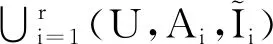
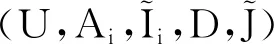
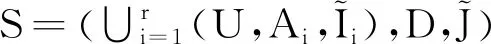
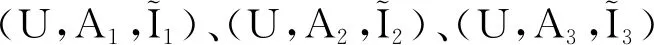
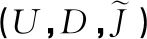
表6 實值形式背景

圖5 表6的實值形式背景的概念格

表7 表6的所有L-實概念

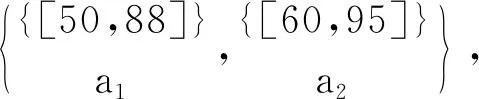
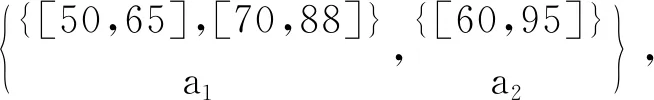
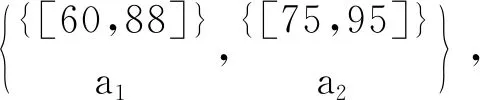
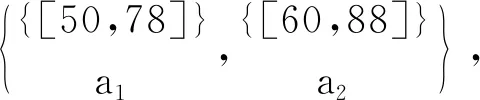
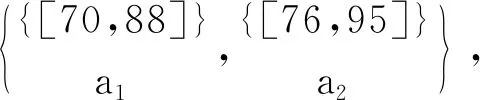
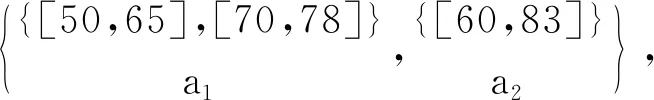
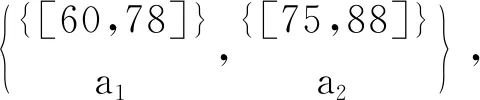
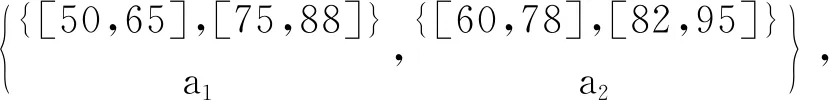
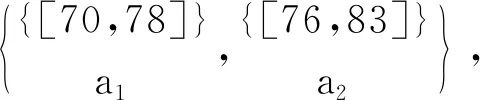
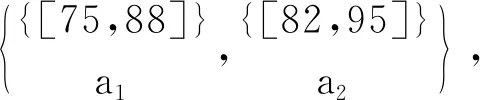
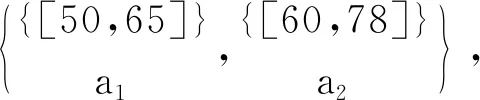
4 結語

本文將多粒度思想引入實值形式概念分析中，提出了多粒度實值形式背景，研究了L-實概念與L-實決策規則隨著粒度空間粗細變化的轉移或演化規律。有關多粒度實值概念與決策規則的結論，既完善了實值概念格理論，又推廣了現有的多粒度形式概念分析方法。

一方面，在粒度空間從粗到細的變化過程中，盡管可以使得數據分析更加具體化，但是計算復雜度也會相應增加，因此需要繼續研究L-實概念與L-實決策規則的演化效率；另一方面，在粒度空間從細到粗的變化過程中，信息會丟失，從而影響L-實概念與L-實決策規則的有效性，所以有待進一步給出多粒度實值形式背景的信息度量方法以及L-實概念與L-實決策規則的有效性評估方法。

另外，為了進一步對多粒度實值形式概念分析理論與方法進行完善，仍需考慮將實值類屬性塊推廣到多粒度實值類屬性塊，即允許條件概念的實值屬性信息來源于不同的粒度空間，從而使得L-實概念與L-實決策規則的知識發現實現深層次的跨粒度層組合。

最后，需要指出的是，本文的討論均針對L-實概念展開。然而，對于實值形式概念分析，除了L-實概念，還有另一種實概念(即S-實概念)，本文未考慮S-實概念的研究情況，主要原因是它將有類似的結論成立，故沒有平推式列出相應的結論。