水平冷凝管在水膜作用下穩態傳熱數值模擬

錢穎燕 周亞素 張恒欽

1 東華大學環境科學與工程學院

2 上海良機冷卻設備有限公司

1 引言

蒸發式冷凝器可以看作是將水冷式冷凝器和冷卻塔結合的高效換熱設備。它利用水膜蒸發將管內制冷劑冷凝時的熱量帶走，再通過空氣強制對流排出熱量，具有節能、節水、冷凝效果好，占地面積小等優[1]。目前，國內外研究人員對蒸發式冷凝器也進行了大量的研究工作。從文獻[2～5]可以知道對于蒸發式冷凝器管外水膜的研究較多。從唐廣棟[6]的研究可以得出，不考慮污垢熱阻，管內冷凝熱阻大約占了總熱阻的25%～35%，水膜熱阻約占了25%～40%，氣液界面熱阻約占23%～40%，而管內冷凝熱阻和水膜熱阻是比較容易通過手段減小的兩個熱阻，因此也有必要對蒸發式冷凝器管內冷凝換熱進行研究。而對于水平管內冷凝，開展的換熱性能研究[7～15]多為一側為制冷劑，另一側為冷卻水或空氣，很少涉及管外降膜蒸發換熱的研究。

基于此，本文運用 EES（Engineering Equation Solver）軟件編程計算，模擬水膜作用下水平冷凝管內換熱性能，研究了冷凝管長度和冷凝溫度對出口干度，換熱量和管內換熱系數的影響，為蒸發式冷凝器的設計及性能優化提供一定的參考。

2 水膜作用下水平冷凝管模型

水平冷凝管在水膜作用下的傳熱過程主要可分為兩個階段，第一階段是管內制冷劑冷凝放出熱量，并通過管壁將熱量傳遞給管外水膜。第二階段則是管外水膜將熱量傳遞給空氣，這是一段復雜的傳熱傳質過程。

制冷劑在冷凝管內一般由過熱區、兩相區和過冷區組成。本文采用分布參數模型對水膜作用下的水平冷凝管進行穩態建模。按制冷劑流動方向沿管程將換熱管劃分為若干個微元段，選這些微元段為控制體進行求解。

2.1 模型假設條件

為了簡化模擬，需要做出以下假設：

1）管內制冷劑沿軸向作一維流動，不用考慮徑向流動。

2）管內制冷劑冷凝溫度為一定值[16]。

3）忽略軸向導熱，只考慮徑向換熱。

4）忽略不凝性氣體影響。

5）忽略管內外污垢熱阻的影響[16]。

6）制冷劑進口蒸汽為對應壓力下的飽和氣體。

7）管外噴淋水和空氣均勻流過冷凝管。

2.2 基本換熱方程

水膜作用下冷凝管段的簡化模型如圖1 所示。按制冷劑流動方向沿管程將冷凝管劃分為若干個微元段，微元段示意圖如圖2 所示。

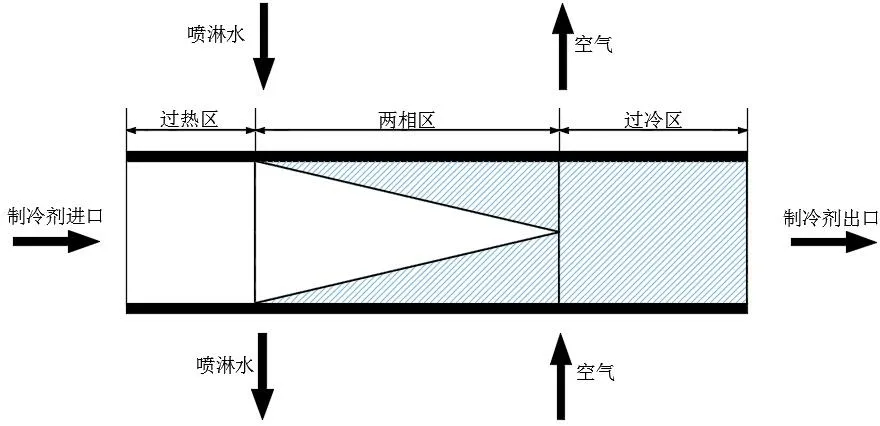
圖1 水膜作用下冷凝管段物理模型示意圖

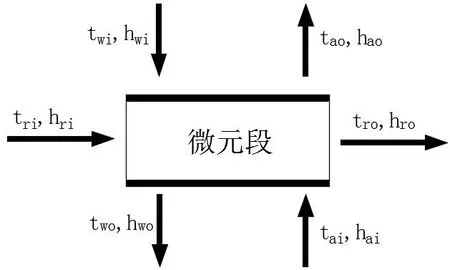
圖2 水膜作用下冷凝管微元段示意圖

1）微元段制冷劑側換熱方程式可表示為：

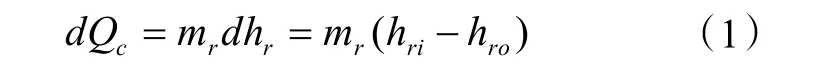
式中：Qc為總換熱量，kW；mr為制冷劑蒸汽流量，kg/s；hri為入口制冷劑蒸汽的比焓，kJ/kg；hro為出口制冷劑液體的比焓，kJ/kg。

2）管內制冷劑換熱量經過管壁傳遞給管外水膜，最終熱量由空氣帶走。

微元段換熱量可表示為：

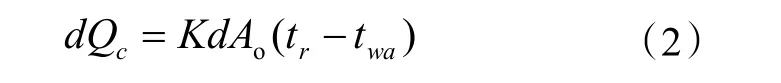
式中：K為制冷劑到管外空氣的總傳熱系數，W/(m2·K)；A0為總的傳熱面積，m2；tr為微元段管內制冷劑側平均溫度，℃；twa為空氣的平均溫度，℃。

忽略污垢熱阻后的制冷劑到管外空氣的總傳熱系數可表示為下式：

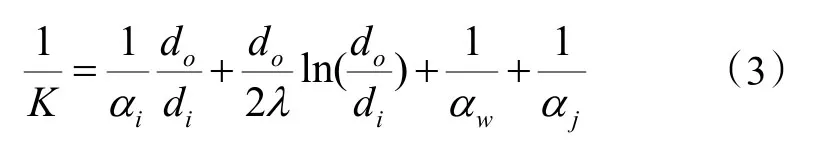
式中：αi為管內流體對流換熱系數，W/(m2·K)；do為換熱管外徑，m；di為換熱管內徑，m；λ為管材的導熱系數，W/(m2·K)；αw為管壁與水膜間的傳熱系數，W/(m2·K)；αj為水膜與空氣之間的當量對流換熱系數，W/(m2·K)。

根據以上公式，由于能量守恒，可以推導出水膜作用下冷凝管微元段長度dL的計算式：

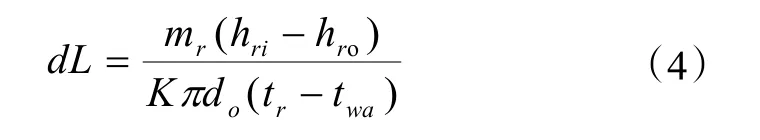
2.3 換熱系數的計算

1）管內制冷劑側換熱系數αi

對于單相區，管內制冷劑側換熱系數采用 Dittus-Boelter[17]公式來計算：

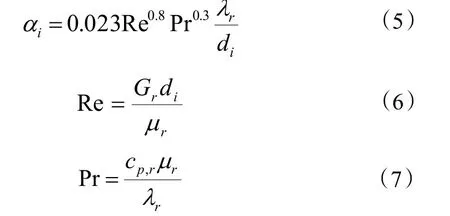
式中：αi為管內流體對流換熱系數，W/(m2·K)；Gr為制冷劑質量流速，kg/(m2·s)；μr為制冷劑動力粘度系數，Pa·s；λr為制冷劑導熱系數，W/(m·K)；cp,r為制冷劑比熱容，J/(kg·K)。

對于兩相區，管內制冷劑側換熱系數則可按下式計算[18]：

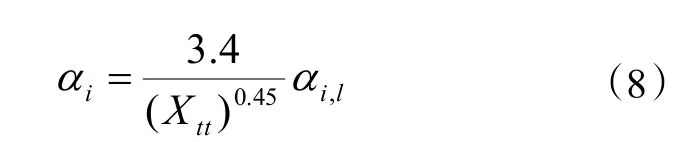
Xtt為兩相區換熱修正系數，計算可按下式：

式中：αi,l為全部為液體時制冷劑的換熱系數，W/(m2·K)，按式（5）計算；x為制冷劑的干度；ρr,v、ρr,l分別是制冷劑氣相和液相的密度，kg/m3)；μr,v、μr,l分別是制冷劑氣相和液相的動力粘度，Pa·s。

2）管壁與水膜間換熱系數αw

Parker 和 Treybal[19]在 McAdams[20]等人得出的管壁與水膜之間的換熱關系式的基礎上，進一步得出了適用于水平管管外水膜與管壁之間的換熱，可如下表所示：

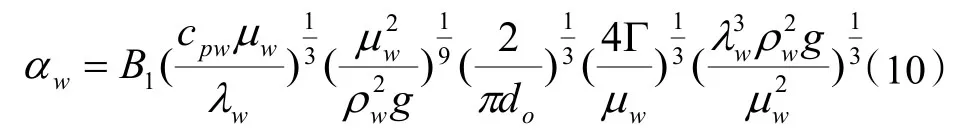
式中：B1為常數，本文取0.332；cpw為噴淋水的定壓比熱容，kJ/(kg·K)；μw為水的動力粘度，kg/(m·s)；λw為水的導熱系數，W/(m·K)；ρw為水的密度，kg/m3；g為重力加速度，m/s2；Γ 為管外噴淋水的噴淋密度，kg/(m·s)。

3）水膜與空氣之間的當量對流換熱系數αj

張祉祐[21]針對管外水膜與空氣間的換熱，把噴淋水與空氣的換熱看成是顯熱交換和潛熱交換兩部分作用，并在此基礎上引入當量換熱系數，以便與管內流體和管外水膜間的傳熱系數統一起來。

水膜與空氣對流換熱系數關聯式為：

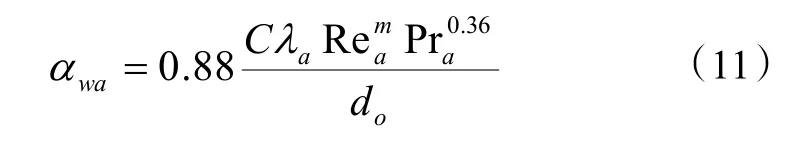
式中：C，m為常數，與空氣流動狀態 Rea和管束排列方式有關，本文C取0.52，m取0.5；Pra則為空氣的普朗特數。

根據文獻[21]可得出當量換熱系數αj表達式為：

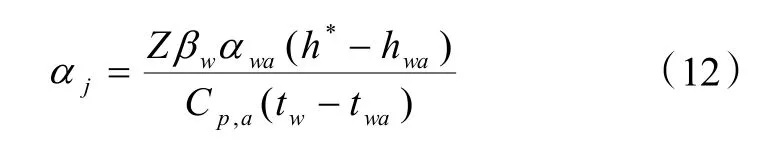
式中：Z為與噴淋水膜有關的系數，本文取0.96；βw是水膜與空氣間接觸面積的修正系數，取1.3～1.5；h*是與噴淋水溫度相對應的飽和空氣的比焓，kJ/kg；hwa為濕空氣的平均比焓，kJ/kg；Cp,a為濕空氣的比熱，kJ/(kg·℃)；twa為空氣的平均溫度，℃。

3 理論計算流程

本文模擬的水平冷凝管相關參數如表1：

表1 水平冷凝管相關參數

計算中給定管外噴淋水噴淋密度為0.047 kg/(m·s)，噴淋水溫21℃，空氣干球溫度25℃，濕球溫度19.5℃，迎面風速2.9 m/s。

模擬計算所用的穩態分布參數模型程序中所用的迭代算法為二分法。具體的算法過程如下：

1）假設制冷劑出口焓值hro。以給定冷凝壓力的制冷劑飽和氣體焓值作為二分法的上限，噴淋水進口溫度下的制冷劑液體焓值作為二分法的下限。取上下限值的算術平均作為制冷劑出口焓值的迭代初始值。

2）從冷凝管出口開始對微元段進行編號計算。

3）將假定的制冷劑出口焓值和冷凝溫度所對應的飽和制冷劑液體焓值比較。如果出口焓值小于飽和液體焓值，則制冷劑處于過冷狀態，計算過冷區長度。反之，制冷劑處于兩相狀態，計算兩相區長度，將過冷和兩相區中每個微元段長度相加得到冷凝管計算管長。

4）將計算管長與實際管長進行比較。如果計算管長大于實際管長，說明假設焓值過小，則以假定焓值取代二分法的下限。如果計算管長小于實際管長，說明假定焓值過大，則把二分法的上限替換成假定焓值，重新計算，即轉向（2），假定焓值根據算數平均值計算。如果滿足要求，則結束計算，輸出結果。

具體計算流程圖如圖3：

圖3 水膜作用下水平冷凝管數值計算流程圖

4 數值計算結果與分析

4.1 冷凝管長度對出口干度，換熱量及管內平均換熱系數的影響

本節在冷凝溫度40℃的條件下，模擬了不同冷凝管長度（4～5.7 m）對出口干度，換熱量及管內平均換熱系數的影響。

對于冷凝器而言，選擇合適的管長使冷凝管出口干度達到0，可以有效降低銅的用量和成本，同時也降低了能耗，提高經濟性。圖4 所示為水平冷凝管長度對出口干度的影響，由圖可知，冷凝管出口干度隨著管長的增加不斷減小。由于冷凝管越長，相同制冷劑質量流量下換熱時間越長，換熱越充分，因此出口干度越小。制冷劑質量流量從0.0044 kg/s 增加到0.0078 kg/s，冷凝管長度增加35.7%，才能使出口干度達到0，在其它參數不變的條件下，當制冷劑質量流量增大時，主流速度也增大，制冷劑蒸汽與管壁之間換熱不充分，出口干度增大，因此需要增加管長來延長換熱時間使制冷劑蒸汽充分冷凝。

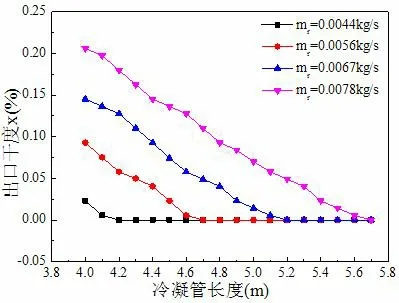
圖4 冷凝管長度對出口干度的影響

圖5，圖6 分別為水平冷凝管長度對管內平均換熱系數和換熱量的影響。從圖中可得知：隨著冷凝管長度增加，管內平均換熱系數基本不變，波動范圍在4 W/(m2·K)內。換熱量隨冷凝管長度增加先不斷增大，后增加趨勢變緩。當管長增到一定長度時，出口干度達到0，管內制冷劑已全部冷凝成液體，繼續增加冷凝管長度，長度增加部分的換熱從潛熱換熱變成顯熱換熱，換熱量較小，因此換熱量增加幅度變小。在制冷劑質量流量為0.0078 kg/s 時，管長從4 m 增加到5.7 m，換熱量增大了26.4%。

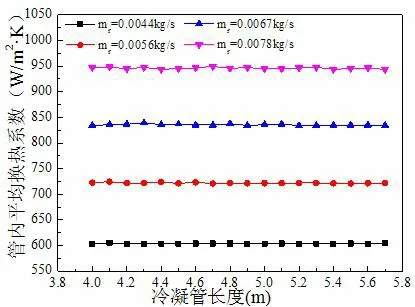
圖5 冷凝管長度對管內平均換熱系數的影響

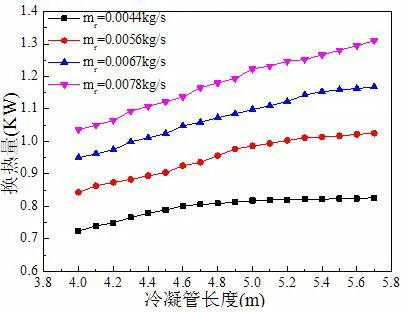
圖6 冷凝管長度對換熱量的影響

4.2 冷凝溫度對出口干度，換熱量及管內平均換熱系數的影響

在管長為4.6 m 的條件下，模擬了不同冷凝溫度（35℃～42℃）對出口干度，換熱量及管內平均換熱系數的影響。

圖7 所示為不同制冷劑質量流量下，冷凝溫度對出口干度的影響。

從圖7 中可以看出，冷凝溫度越高冷凝管出口干度越小，因為冷凝溫度升高導致傳熱溫差變大，增加了傳熱驅動力，加強了換熱效果，所以出口干度減小。在制冷劑質量流量為0.0078 kg/s 時，冷凝溫度從35℃增加到42℃，出口干度減小了88.7%。

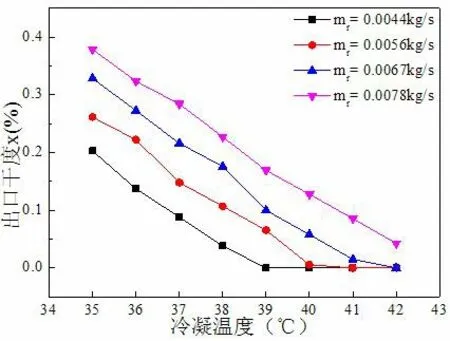
圖7 冷凝溫度對出口干度的影響

圖8 為不同制冷劑質量流量下，冷凝溫度對換熱量的影響。

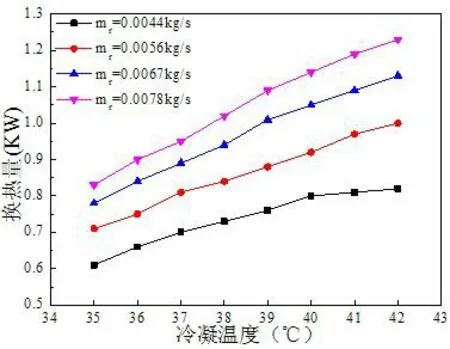
圖8 冷凝溫度對換熱量的影響

從圖8 中可以看出：

1）同一冷凝溫度下，換熱量均隨著制冷劑質量流量的增大而增大。因為質量流量增大使得制冷劑流速增大，氣液界面剪切力變大，液膜變薄，熱阻變小，從而增強了換熱效果。在冷凝溫度為40℃時，制冷劑質量流量從0.0044 kg/s 增加到0.0078 kg/s，換熱量增加了42.5%。

2）制冷劑低質量流量下，冷凝溫度對換熱量的影響比高質量流量下的影響小。當質量流量為0.0044 kg/s 時，冷凝溫度從35℃增至42℃，換熱量增加了34.4%；當質量流量為0.0078kg/s 時，冷凝溫度從35℃ 增至42℃，換熱量增加了48.2%。這是因為隨著冷凝溫度升高，傳熱溫差增大，增大了傳熱驅動力。在低質量流量下，隨著冷凝溫度升高，制冷劑蒸汽密度增大，導致流速降低，冷凝液膜厚度增加，熱阻增大，會減小換熱量，但相對而言，傳熱溫差對換熱量的增加作用更強，因此換熱量隨著冷凝溫度升高而增大。而在高質量流量下，冷凝溫度變化對液膜厚度影響不明顯，所以高質量流量時，換熱量隨冷凝溫度的變化趨勢比低質量流量時明顯。

圖9 是不同制冷劑質量流量下，冷凝溫度對管內平均換熱系數的影響。

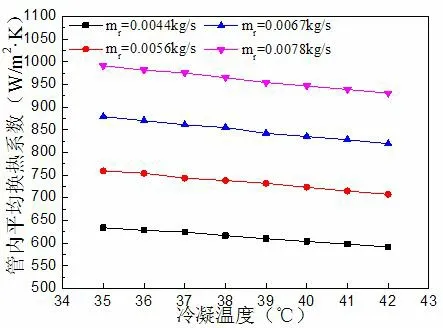
圖9 冷凝溫度對管內平均換熱系數的影響

從圖9 中可以看出：

1）其它參數條件不變時，管內平均換熱系數隨制冷劑質量流量的增大而增大，冷凝溫度為40℃時，質量流量從0.0044 kg/s 增加到0.0078 kg/s，管內平均換熱系數增加了56.8%。

2）與換熱量相反，其它參數不變時，管內平均換熱系數隨冷凝溫度的升高而減小。在制冷劑質量流量分別為0.0044 kg/s，0.0056 kg/s，0.0067 kg/s 和0.0078 kg/s 時，冷凝溫度從35℃增至42℃，管內平均換熱系數分別減小了7.14%，7.30%，7.29%和6.48%。

5 結論

本文利用 EES 軟件模擬計算了在水膜作用下水平冷凝管的換熱情況，得出如下結論：

1）冷凝管出口干度隨著管長的增加不斷減小。當制冷劑質量流量從0.0044 kg/s 增加到0.0078 kg/s 時，冷凝管長度增加35.7%，才能使出口干度達到0。管內平均換熱系數隨冷凝管長度增加基本不變。換熱量隨冷凝管長度增加先不斷增大，后增加趨勢變緩。當制冷劑質量流量為0.0078 kg/s 時，管長從4 m 增加到5.7 m，換熱量增大了26.4%。

2）冷凝溫度越高冷凝管出口干度越小。在制冷劑質量流量為0.0078 kg/s 時，冷凝溫度從35℃增加到42℃，出口干度減小了88.7%。制冷劑低質量流量下，冷凝溫度對換熱量的影響比高質量流量下的影響小。當質量流量為0.0044 kg/s 時，冷凝溫度從35℃增至42℃，換熱量增加了34.4%。當質量流量為0.0078 kg/s 時，冷凝溫度從35℃增至42℃，換熱量增加了48.2%。與換熱量相反，其它參數不變時，管內平均換熱系數隨冷凝溫度的升高而減小。