幾何距離公式的推理與應用
四川師范大學數學科學學院(610068) 勾藝茹
四川省阿壩州茂縣中學(623200) 李述芬
四川師范大學數學科學學院(610068) 邵 利
一、引言
幾何中最基礎的元素為“點”,“點”運動成“線”,“線”運動成“面”,“面”運動成“體”。按空間維度,幾何可歸納為從“點”出發到一維的“線”,再從一維的“線”到二維的“面”,接著從二維的“面”到三維的“體”三類。以上變化可謂是環環相扣。數軸、平面直角坐標系、空間直角坐標系則是按照空間維度的順序展開的。本文從低維進階到高維空間的視角介紹幾何距離相關公式的推導與應用。
二、幾何距離公式
幾何中點、線、面三者之間的距離公式按排列組合方式進行分類,有點與點、點與線、點與面、線與線、線與面、面與面六種類型(注:線、面等相關距離問題,需要平行關系才有意義)。其中最基礎的類型為點與點、點與線、點與面。
(一)兩點的距離公式
數軸、平面直角坐標系、空間直角坐標系中的兩點的距離公式見表1。
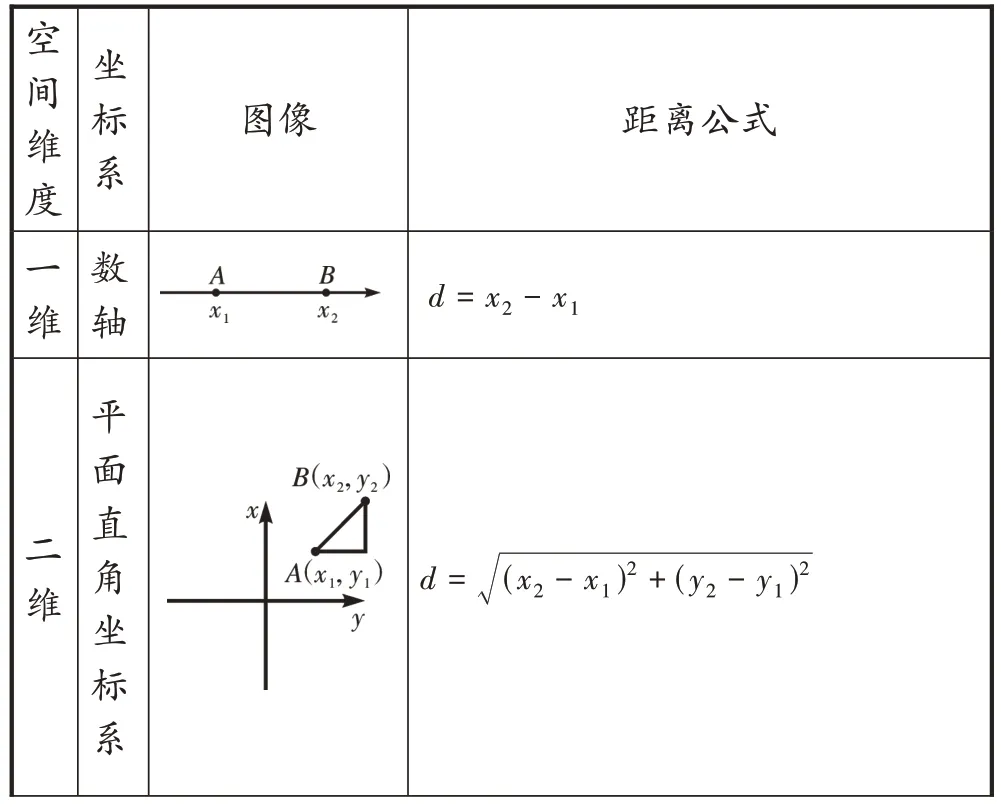
表1 兩點的距離公式

續表
(二)“一生二”——由兩點的距離公式到點到直線的距離公式
(1)定義:過點作目標直線的垂線,這點到垂足的距離。
設直線l的方程為Ax+By+C=0,點P的坐標為(x0,y0),則點P到直線l的距離
(2)公式推導:
如圖1所示,過點P作直線l的垂線,垂足為M。

圖1
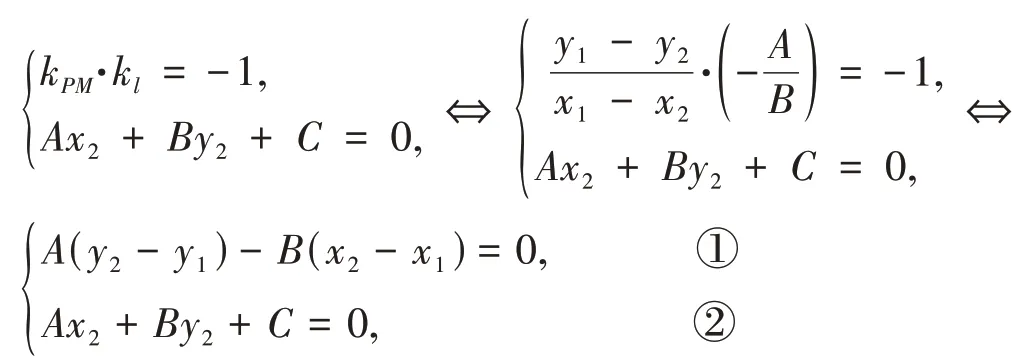
將②兩邊同時減去Ax1+By1+C,得

將①③式兩邊分別平方,得
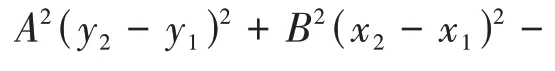

(三)“二生三”——由點到直線的距離公式到點到面的距離公式
高中教材在平面解析幾何中涉及點到直線的距離公式,此公式為點到直線的距離求解提供了便利。然而對于立體幾何中點到平面的距離公式,教材未給出相應的內容。
(1)公式猜想
【點到線的距離】設直線l的方程為Ax+By+C=0,點P的坐標為(x0,y0),則點P到直線l的距離
【點到面的距離】設平面α的方程式為Ax+By+Cz+D=0,點P的坐標為(x0,y0,z0),則點P到平面α的距離d=
(2)公式推導
前提:在點到面的距離公式推導過程中,均要用到平面法向量,因此先對平面法向量進行說明。
設(x1,y1,z1)和(x2,y2,z2)為平面內任意兩個點,由點在面上得:

由⑥-⑦得
A(x1-x2)+B(y1-y2)+C(z1-z2)=0,
即(A,B,C)·(x1-x2,y1-y2,z1-z2)=0。
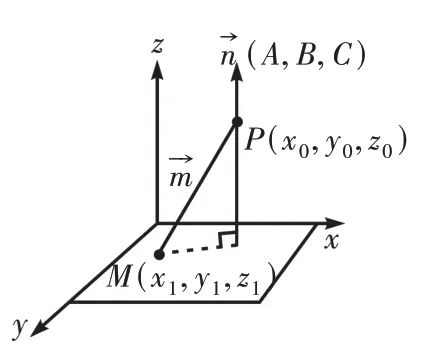
圖2


圖3

(3)學以致用
下面利用點到面的距離公式,解決立體幾何距離問題以及一類不等式問題。
[例1](點面距離)如圖4,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分別是BC,BB1,A1D的中點。求點C到平面C1DE的距離。
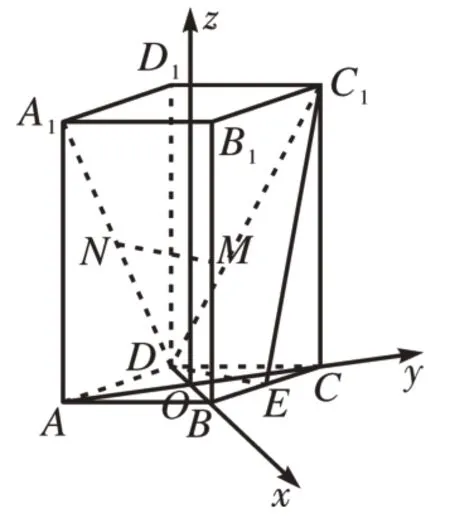
圖4
分析:求點到平面的距離,需要知道點的坐標以及平面方程。首先建立直角坐標系,其次通過C1,D,E三點確定平面C1DE的方程,最后將點與平面數據代入公式求解距離。
解答:如圖4,四邊形ABCD為菱形,則連接AC、BD交點為O,且AC⊥BD。以點O為原點建立空間直角坐標系O-xyz。
∵AA1=4,AB=2,∠BAD=60°,E是BC的中點。∴B(1,0,0),D(-1,0,0),C
設平面C1DE的方程式為:ax+by+cz+d=0,
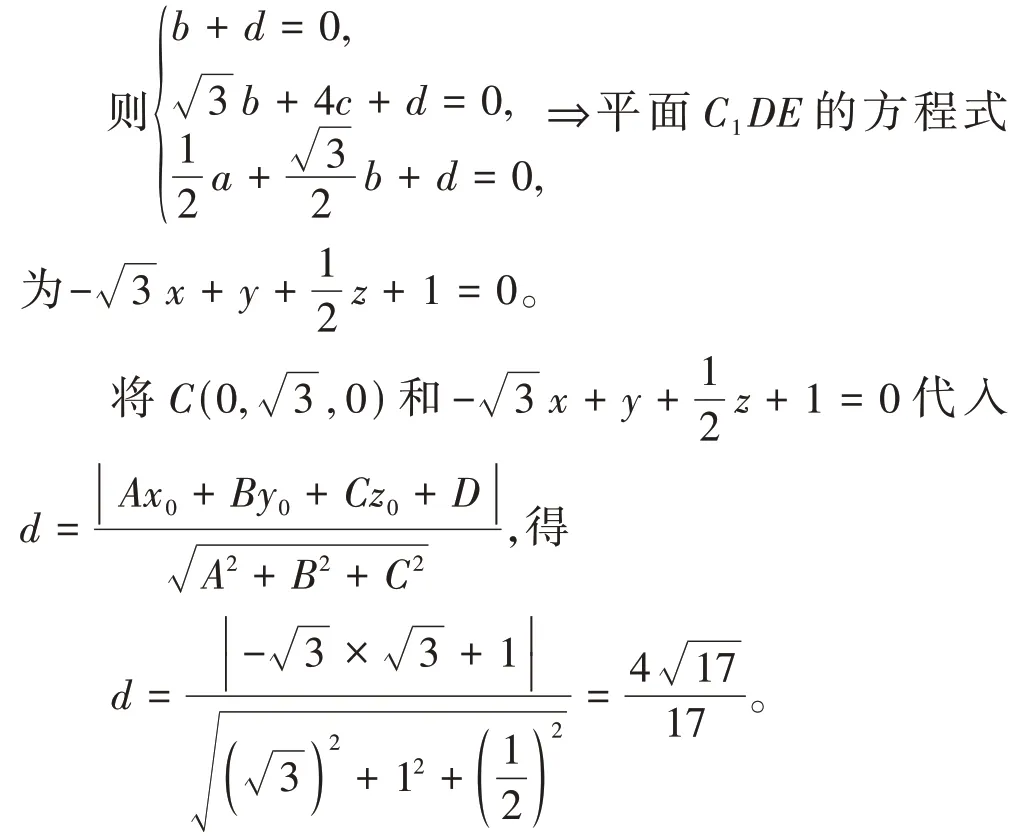
[例2](面面距離)已知平面α:2x+3y+z+5=0,平面β:2x+3y+z+18=0。求兩平面的距離。
分析:求解兩平面之間的距離,可以轉化為求解一平面上的一點到另一平面的距離,因此,在平面α找一點P,求點P到平面β的距離。
解答:設P(x0,y0,z0)為平面α上的一點,則滿足2x0+3y0+z0+5=0,P到平面β的距離為
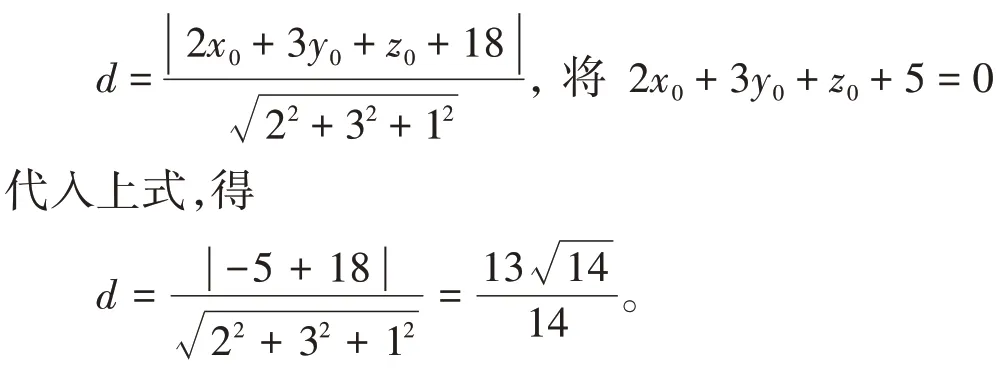
兩平面的距離求解公式:
平面α:Ax+By+Cz+D1=0,平面β:Ax+By+Cz+D2=0,平面α與平面β的距離為

[例3]設x,y,z∈R,且x+y+z=1。
(1)求(x-1)2+(y+1)2+(z+1)2的最小值。
(2)(x-2)2+(y-1)2+(z-a)2≥證明:a≤-3或a≥-1。
分析:將題干與問題進行轉化。
已知平面x+y+z-1=0,第(1)問求平面外一點(1,-1,-1)到平面的距離的平方;
第(2)問要求證明點(2,1,a)到平面的距離的平方為時,a的范圍為a≤-3或a≥-1。
解 答:(1)設平面α為x+y+z-1=0,點P(1,-1,-1)為平面外一點,則點P到平面α的距離的平方為
(2)設平面α為x+y+z-1=0,點Q(2,1,a)為平面外一點,點Q到平面α距離的平方最小值為則-3 或a≥-1。
三、小結

正如《道德經》中的“道生一,一生二,二生三,三生萬物”,幾何也秉承著一定的邏輯不斷衍生變化。學生在學習幾何時可采用先觀察、再猜想、最后證明的方式抓住其中的邏輯規律,借助相似性展開聯想,進行遷移,發展直觀想象核心素養。

