函數問題中常見的轉化思想

廣東惠州市惠陽區第一中學高中部（516000） 劉錦濃

函數是高中數學的基礎，它知識點多，覆蓋面廣，綜合性強，很容易與其他知識建立聯系。解決函數問題所需的轉化思想是重要的數學思維策略，它在數學解題中應用廣泛。運用轉化思想可以將陌生變為熟悉，將復雜變為簡單，將抽象變為直觀，從而有效解決問題。本文主要探討函數問題中常見的轉化思想。

一、數與形的轉化

數形結合，實質上就是將抽象的數學語言與直觀的幾何圖形結合起來，實現抽象概念與具體形象的聯系與轉化。

（一）以形助數

［例1］設方程log3x+x-3=0的根為x1，方程3x+x-3=0的根為x2，求x1+x2的值。

分析：本題若直接解出x1，x2的值，再求x1+x2是不現實的。觀察兩個方程發現，y=log3x與y=3x互 為反函數，可利用反函數的圖像關于直線y=x對稱的性質，輔以圖像解題。

解：將原方程化為log3x=3-x，3x=3-x，方程log3x+x-3=0 的根為x1，實質上是函數y=log3x與y=3-x圖像的交點的橫坐標；方程3x+x-3=0 的根為x2，實質上是函數y=3x與y=3-x圖像的交點的橫坐標。如圖1，設其交點分別為A、B，函數y=x與y=3-x圖像的交點為P。

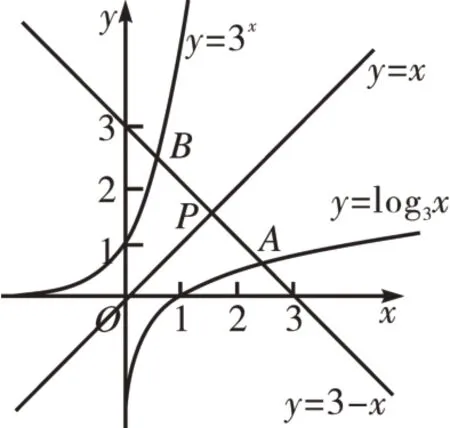
圖1

因為y=x與y=3-x垂直，且函數y=log3x與y=3x的圖像關于直線y=x對稱，所以點A、B關于點P對稱，易得，所以x1+x2=3。

評析：本題主要是把方程轉化為函數的圖像相交求解。由圖形分析數量間的本質聯系，解決數學問題時能做到快、準，解題往往事半功倍。

（二）以數助形

［例2］如圖2，已知OPQ是半徑為1，圓心角為的扇形，C是扇形弧上的動點，四邊形ABCD是扇形的內接矩形。記∠COP=α，當角α取何值時，矩形ABCD的面積最大？并求出這個最大面積。

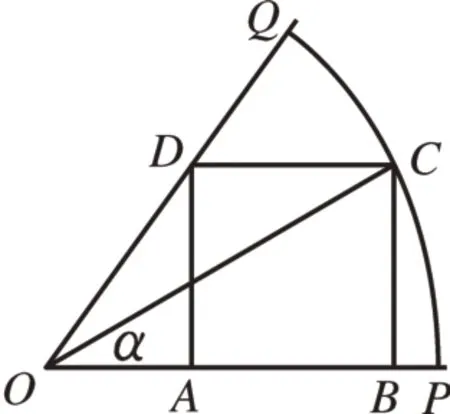
圖2

分析：要求當角α取何值時，矩形ABCD的面積最大，可分兩步進行：（1）找出矩形ABCD的面積S與α之間的函數關系；……