基于量值傳遞的經緯儀檢定裝置不確定度評定方法

陳向榮 梁鈺坤 趙航 姜琳 劉小朋

[摘? ? 要]在建立計量標準的過程中，針對數據樣本進行合理且科學的不確定度評定是保證計量標準技術性能滿足量值傳遞的重要環節。文章介紹了測量不確定度的概念和評定的兩類數據處理方法，又以經緯儀檢定裝置為例，詳細分析了不同數據處理方法產生的誤差，最終采用基于量值傳遞的評定方法對經緯儀檢定裝置這一計量標準進行評定。

[關鍵詞]不確定度;數據處理;經緯儀;計量標準

[中圖分類號]TH761.1 [文獻標志碼]A [文章編號]2095–6487（2022）04–0–03

Uncertainty Evaluation Method of Theodolite Verification?Device Based on Quantity Transfer

Chen Xiang-rong，Liang Yu-kun，Zhao Hang，Jiang Lin，Liu Xiao-peng

[Abstract]In the process of establishing measurement standards， a reasonable and scientific uncertainty assessment for data samples is an important link to ensure that the technical performance of measurement standards meets the transfer of value. This paper introduces the concept of measurement uncertainty and two types of data processing methods for evaluation， and takes the theodolite verification device as an example to analyze the errors caused by different data processing methods in detail. This measurement standard is evaluated.

[Keywords]uncertainty; data processing; theodolite; measurement standard

科學認識客觀世界是逐漸逼近真實的過程，偏離真實時人們會減少認知不足;合理地評估不確定性則尤為重要，計量學將成為科技進步的重要動力。研究科學表示測量結果的可靠程度，是現代科學關注的重點問題[1]。

1 測量不確定度簡介

1.1 理論定義

表示測量結果質量的術語有許多種，實踐中最常用的是測量誤差相關理論。誤差即測量值減去被測量真值，單純用誤差值來表征相關測量精度不夠嚴謹的。測量誤差按可以分為隨機和系統誤差，誤差評定方法不同使其難以作為統一的測量精度指標[2]。

測量不確定度是表征被測量值分散性的非負參數，不存在相關性質上的分類，是以統計學特征參數標準差量化表示標準不確定度;標準u及擴展不確定度U具有對應的包含概率，依據統計學方法得到特征值可以為測量結果給出值得信賴的參考依據，利用統計學的概率意義進行評定是現代測量精度理論的重要指標。測量不確定度在評定過程中圍繞包含概率來量化，符合統計學對具體問題預測評定的指導思想。

1.2 理論的意義

測量不確定度理論是測量科學理論體系重點研究內容，也是保證獲取信息可靠性的重要手段[3]。如何合理科學地對測量數據進行處理，是不確定度評定中最為關鍵的一環。同一組數據，如果評定方法選擇不恰當，會導致最終的不確定度評定與實際不符，影響計量標準的技術性能參考和量值傳遞價值。本文將結合實際工作中進行計量標準不確定度評定時，針對不同的數據樣本分析采用的數據處理方法進行解釋說明，為測量不確定度的評定提供參考。

2 測量數據處理

2.1 測量重復性的數據處理

2.1.1 處理方法簡介

提到數據處理的方法，第一選擇是貝塞爾公式——用于表示單次測量結果的標準不確定度。貝塞爾公式計算得到的是實驗標準差s，當測量次數n較小時，計算得到的實驗標準偏差除了隨機誤差會增大外，還存在較大的系統誤差。

實驗標準偏差也可以用極差法計算，對被測量X做n次獨立觀測，在可以估計被測量X接近正態分布下，單次測量結果的實驗標準偏差可按下式近似地評定：

式中，C為極差系數，由表1給出，其值與測量次數n有關。

國家計量技術規范JJF 1059.1—2012《測量不確定度評定與表示》的4.3.2.3中指出：一般在測量次數較少時，可采用極差法獲得實驗標準偏差。當被測量滿足正態分布時，測量次數不大于9時，極差法將優于貝塞爾公式法。通常使用極差法的測量次數以4～8次為宜。

測量次數較小時，貝塞爾法給出的實驗標準偏差s并不是標準偏差σ的無偏估計，存在較大的系統誤差。故測量次數較少時極差法是首選數據處理方法[4]。

2.1.2 數據處理實例

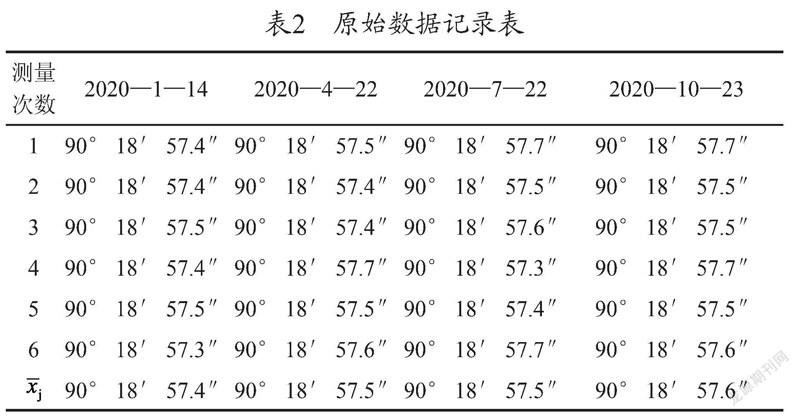
以經緯儀測角架水平方向穩定性考核為例子，在20±10℃下，用經緯儀對測角架1號目標與3號目標之間角度在一年內進行觀測，每季度觀測一次，每次進行6次觀測，取平均值，利用極差法計算sm，見表2。

與擴展不確定度U=0.20″進行對比，依據sm是否小于U進行穩定性判斷，結論是穩定性合格。

如果采用貝塞爾公式法進行計算，結果如下：

此時可以看到，穩定性誤差變成了0.08″，與極差法對比，誤差為20 %;即使此法算出的穩定性誤差較小，但因為測量次數較少結果并不如極差法可靠。這種誤差是十分巨大的，究其原因是貝塞爾法給出的實驗標準偏差sm并不是標準偏差σ的無偏估計，存在較大的系統誤差。29CB9F56-C8DB-4AF1-BD92-CFD383F2406D

以上例子驗證了測量次數較少時，就計算不確定度的標準偏差而言，極差法應作為首選方法。即使在測量次數較少的情況下，極差法也不見得優于貝塞爾法。就方差而言，無論測量次數多少，極差法的自由度均比貝塞爾法小，即貝塞爾法的方差將比極差法更準確。

因此，在測量不確定度評定中，當僅考慮多次測量的實驗標準差或在合成標準不確定度中A類分量占優勢的情況下，測量次數不大于9次時極差法將優于貝塞爾法[4]。

2.2 非測量重復性的數據處理

2.2.1 處理方法簡介

依據其他信息來源進行標準不確定度評定簡稱為B類評定。B類評定中帶有某種主觀的因素，如何恰當并合理地給出B類評定是不確定度評定的關鍵問題之一。

總體來看，B類不確定度評定中，基本處理方法為或，即利用擴展不確定度或半寬度與包含因子的關系求出。不同分布下包含因子k取值不同，這是尤為需要注意的[5]。

2.2.2 數據處理實例

以經緯儀望遠鏡照準時引入的非測量重復性誤差為例，通過查詢設備說明書，經緯儀望遠鏡照準誤差為0.5″，考慮到每照準1次需要讀數2次，則有

如果沒有考慮到每照準一次需要讀數兩次，誤認為望遠鏡照準誤差服從正態分布。此時k=3，則有

通過上述結果，可以看到不同的分布選擇的k不同相關分量也不同，誤差可達50 %。如果在不確定度分析過程中多幾處這樣的誤差，就會導致整個計量標準的不確定度評定出現重大偏差，無法滿足量值傳遞相關要求。

因此，在非測量重復性的數據處理中更須科學合理地進行分析，選擇合適的處理方法;在不確定如何選擇k值時可以參考以往評定示例或者典型示例，在日常工作中也須注意積累經驗。

3 計量標準的數據處理

3.1 合成標準不確定度處理方法簡介

實際使用過程中，若僅考慮無明顯相關性的不確定度分量，則合成標準不確定度由下列公式確定

相關系數的實驗測量需耗費大量時間。測量不確定度評定應盡可能避免由實驗測量相關系數[6]。

3.2 數據處理實例

以經緯儀檢定裝置計量標準的不確定度評定為例，確定測量原理：根據GJB 5073—2004《全站式電子速測儀檢定規程》，電子經緯儀的一測回水平方向標準偏差檢定按照“全圓方向法”測量，利用了平面圓周360°的自然基準;一測回垂直角標準偏差采用常角觀測法。

分析不確定度來源：計算一測回水平方向標準偏差時需要各測回觀測值與平均值之差，不需要標準的水平角度值;計算一測回垂直角標準偏差時也需要各測回觀測值與平均值之差，不需要標準的垂直角度值。一測觀測目標固定，則計量標準的不確定度來源主要是其在檢定過程中水平目標或者垂直目標的定位重復性。

根據分析的不確定度來源進行計量標準的不確定度評定，最后形成計量標準的不確定度報告如下：

（1）經緯儀測角架：水平方向U=0.2″（k=2）;豎直方向U=0.5″（k=2）。

（2）經緯儀全功能檢定儀：水平方向U=0.3″（k=2）;豎直方向U=0.5″（k=2）。

如果在分析過程中錯誤考慮不確定度來源，不僅違背了嚴謹科學的準則，還會高估不確定度，可能導致最終的評定結果不符合量值傳遞的要求。

根據計量標準重復性ua1=0.14″和經緯儀望遠鏡照準目標標準偏差ua2=0.12″進行A類標準不確定度ua的計算，

分析B類標準不確定度ub的來源，主要包括測角架水平角的穩定性、測量誤差和平行光管設計理論誤差;誤差服從正態分布，取置信概率p=90%，查正態分布表得kp=1.645。擴展不確定度取k=2。計算如下：

（1）測角架水平角的穩定性——儀器限差為0.2″，則a=0.2″：

（2）測量誤差——TM5100-A電子經緯儀最小讀數為0.1″，則取半寬度a=0.05″：

（3）平行光管設計理論誤差——根據資料此誤差為0.1″，有a=0.1″：

B類標準不確定度ub：

此時計算合成不確定度：

擴展不確定度U：

U=kuc=0.46″（k=2）

與經緯儀測角架水平方向不確定度U=0.2″（k=2）對比，誤差達130 %，而且因為極大地高估了不確定度數值，導致經緯儀檢定裝置不滿足量值傳遞要求，影響計量標準的使用。這個示例也說明評定不確定度需要具體情況具體分析，針對不同的計量標準選擇合適的方法[7]。

4 結束語

標準不確定度的評定方法是不確定度理論的核心問題，不同的數據處理方法對于評定結果有著巨大影響;上述兩類評定方法難以解決隨機復雜過程的不確定度分析和量化問題，未來應在經典評定方法的基礎上，基于蒙特卡洛原理和貝葉斯統計，建立針對復雜測量任務的動態不確定度評定體系，為有效地預測及評定復雜隨機過程的動態不確定度提供相關原理支持和科學依據[8]。

參考文獻

[1] 葉培德.測量不確定度理解評定與應用[M].北京：中國質檢出版社，2013.

[2] Cox M，Harris P.GUM anniversary issue，Foreword[J].Metrologia，2014（4）：141-143.

[3] 程銀寶，陳曉懷，王漢斌，等.基于精度理論的測量不確定度評定與分析[J].電子測量與儀器學報，2016，30（8）：1175-1182.

[4] 林洪樺.測量誤差與不確定度評估[M].北京：機械工業出版社，2009.

[5] 通用計量術語及定義：JJF 1001—2011[S].

[6] 王中宇，夏新濤，朱堅民.測量不確定度的非統計理論[M].北京：國防工業出版社，2000.

[7] 倪育才.實用測量不確定度評定[M].北京：中國質檢出版社，中國標準出版社，2013.

[8] 程銀寶.現代不確定度理論及應用研究[D].合肥：合肥工業大學，2017.29CB9F56-C8DB-4AF1-BD92-CFD383F2406D