平面轉體施工斜拉橋的索力與主梁線型協調優化分析

白海峰，宋慶

(大連交通大學 土木工程學院，遼寧 大連 116028)

采用平面轉體法施工的斜拉橋，在整個施工過程中，結構內部高次超靜定，經歷多次體系轉換，受力復雜.主梁脫架、大懸臂狀態轉動與懸臂端合龍施工，這些轉體前后的施工作業對橋梁結構施工階段的索力與主梁線型提出了嚴格的限制，常用施工階段計算分析方法確定的施工狀態存在較大的優化空間，因此，對轉體施工過程進行獨立的分析、優化是非常必要的.

目前，斜拉橋的施工階段預演分析方法包括：正裝迭代法[1]、倒拆-正裝迭代法[2]和無應力控制法[3]，這些方法的共同點是由設計成橋狀態反演施工狀態，并滿足施工階段的安全性要求，因為轉體施工的特殊性，直接采用上述方法很難滿足轉體施工的嚴苛要求.謝劍[4]采用零位移法與應力平衡法確定某獨塔斜拉橋轉體前的施工狀態；曾甲華[5]針對不對稱轉體施工獨塔斜拉橋，構思了適用于該類橋式的合理轉體平衡狀態和優化思路，基于非線性空間有限元手段，采用非線性影響矩陣技術，實現了龍巖大橋轉體平衡狀態的優化；孫全勝[6]分析了斜拉橋水平轉體施工主梁脫離支架的影響，采用了在梁體一側加沙袋的方法克服主梁在脫離支架后的不平衡彎矩，在綏芬河斜拉橋轉體施工中證明該方法可行；Liu[7]研究了一座獨塔非對稱混合梁斜拉橋在旋轉施工過程中不同施工階段橋梁的撓度和應力以及塔架的變形，研究的結果為平面轉體斜拉橋的現場精確閉合提供了有價值的參考；Wang[8]提出了一種有效的計算框架，即采用頂推法架設斜拉橋的系統轉換過程(STP)最佳兩階段張緊計劃，為復雜施工過程中斜拉橋的系統轉換過程提供有效的最優張緊策略.

本文以沈陽市昆山西路與304國道連接線高架橋主橋155 m+120 m獨塔單索面斜拉橋為工程背景，采用Midas/Civil 2019軟件建立有限元數值模型，生成結構變形、內力與斜拉索張拉力的影響矩陣，以此建立數學優化函數，求解得到優化后的斜拉橋轉體前懸臂狀態的索力與主梁線型；以此施工狀態作為目標狀態，采用無應力狀態控制法求解斜拉索初次張拉力，分析二次調整索力之前的全部施工工程，驗算施工狀態是否合理.

1 轉體前懸臂狀態的優化方法

1.1 優化函數的建立

影響矩陣是影響向量的所有元素分別發生單位變化時，引起被調向量而產生的變化依次排列形成的矩陣.對于斜拉橋來說，即為在滿足線性疊加原理的基礎上，斜拉索施加單位張拉力時，結構位移、內力、應力、支反力、索力等產生的變化所形成的矩陣[9].影響矩陣法的基本原理可表述為結構線性疊加的調值計算：

[C]{x}={D}

(1)

式中，[C]為影響矩陣，{x}為施調向量，[D]為受調向量[10].

對于斜拉橋平面轉體施工，轉體過程中結構處于兩側大懸臂狀態，主梁線型是優先考慮的控制因素，因此，以主梁截面豎向位移平方和為優化目標函數.

(2)

式中，{μi}為主梁截面豎向位移.

在平面轉體過程中，將結構控制在預定的平衡狀態是實現準確合龍與安全轉體的必備條件.平面轉體、支架脫離與合龍施工對索力的限制條件可作為目標函數的約束條件，使得數學優化模型最終得出滿足施工要求的初張索力，公式可表示為：

(3)

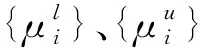
優化目標函數經過變形可得：

minf(t)=0.5×{t}T[H]{t}+{f}T{t}

(4)

式中，f(t)為優化目標函數，自變量{t}為拉索張拉力，[H]、{f}T為算式變形系數矩陣、向量.

1.2 優化計算流程

斜拉橋平面轉體施工狀態的優化流程如圖1所示.其中，無應力狀態法求解施工索力詳見文獻[3].

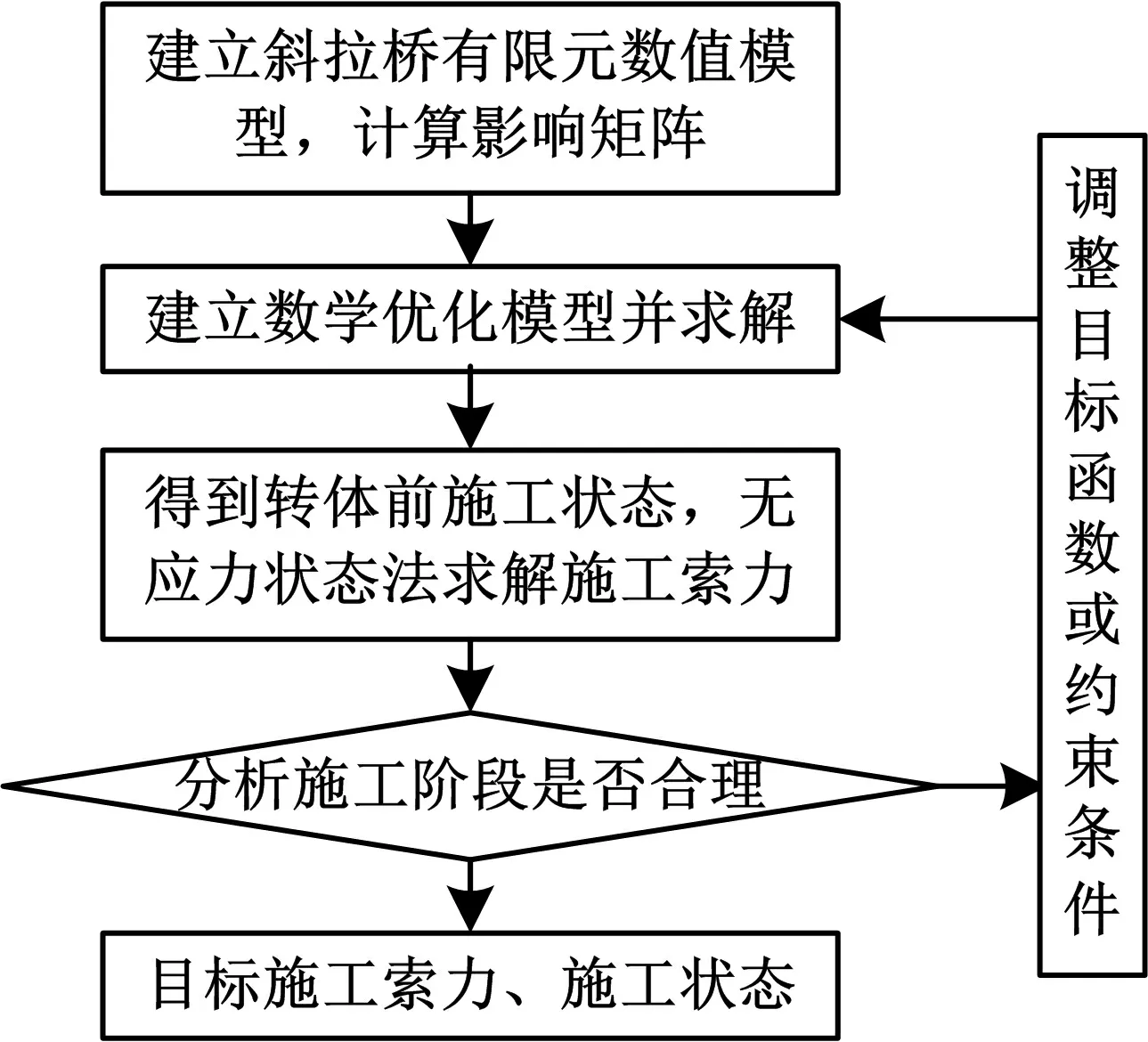
圖1 施工狀態優化流程

2 工程應用實例

2.1 工程概況

沈陽市昆山西路與304國道連接線高架橋主橋結構為155 m + 120 m非對稱獨塔單索面斜拉橋，主梁結構為單箱三室鋼箱梁，全橋鋼主梁劃分成44個梁段，共13種類型；索塔為獨塔鋼箱結構，橋面以上5.4 m范圍內，主塔為等截面，截面尺寸為3.0 m×6.5 m；橋面以上9.0 m到塔頂，主塔為等截面，截面尺寸為3.5 m×6.5 m；5.4～9.0 m主塔截面線性變化；塔梁固結體系，上部結構與橋墩采用支座連接；斜拉索采用平行鋼絲拉索體系，鋼絲采用Φ7 mm環 氧 涂 層 高 強鋼絲， 鋼 絲強度fpk=

1 670 MPa.斜拉索采用定型產品，規格分別為PES7-109、PES7-151、PES7-187.主、邊跨分別布置11對斜拉索；總體布置如圖2所示.

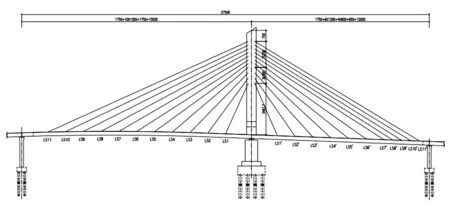
圖2 立面總體布置圖

轉體部分主梁跨徑為149.2 m+115.6 m，邊跨配重為澆筑混凝土塊.施工采用以球鉸中心支撐為主、環道支撐為輔的轉動體系.轉體結構設置在主塔塔柱底部，由轉盤、球鉸、撐腳、環形滑道、牽引系統和助推系統等部分組成，如圖3所示.

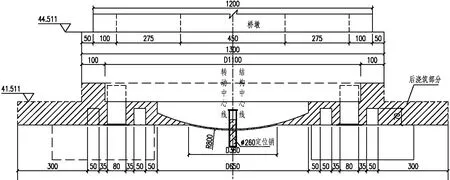
圖3 轉體系統示意圖

2.2 數值模型

根據工程設計圖紙與施工組織文件，使用軟件Midas/Civil2019建立A、B兩個有限元數值模型，模型A用作轉體前懸臂狀態的結構靜力分析，如圖4(a)所示；模型B用作結構施工階段分析，如圖4(b)所示，模型計算參數詳見表1.模型A中，主梁、索塔采用魚骨梁單元模擬，斜拉索采用桁架單元，共有單元235個，節點258個，荷載作用考慮自重、橫隔板等效力以及一期配重，主墩與主梁臨時固結約束全部線位移、角位移.模型B中，結構單元在模型A的基礎上增加兩側合攏段，斜拉索采用索單元模擬(迭代計算處理幾何非線性)，共有單元243個，節點266個；荷載作用在模型A的基礎上增加二期配重與橋面鋪裝，只受壓彈性連接與限制線位移節點模擬滿堂支架，位置選取在主梁節段間隙，塔底節點處支座限制除立面角位移以外其他位移，邊墩支座約束主梁扭轉角位移、橫向與豎向線位移，其余設置與模型A相同.

(a) 模型A

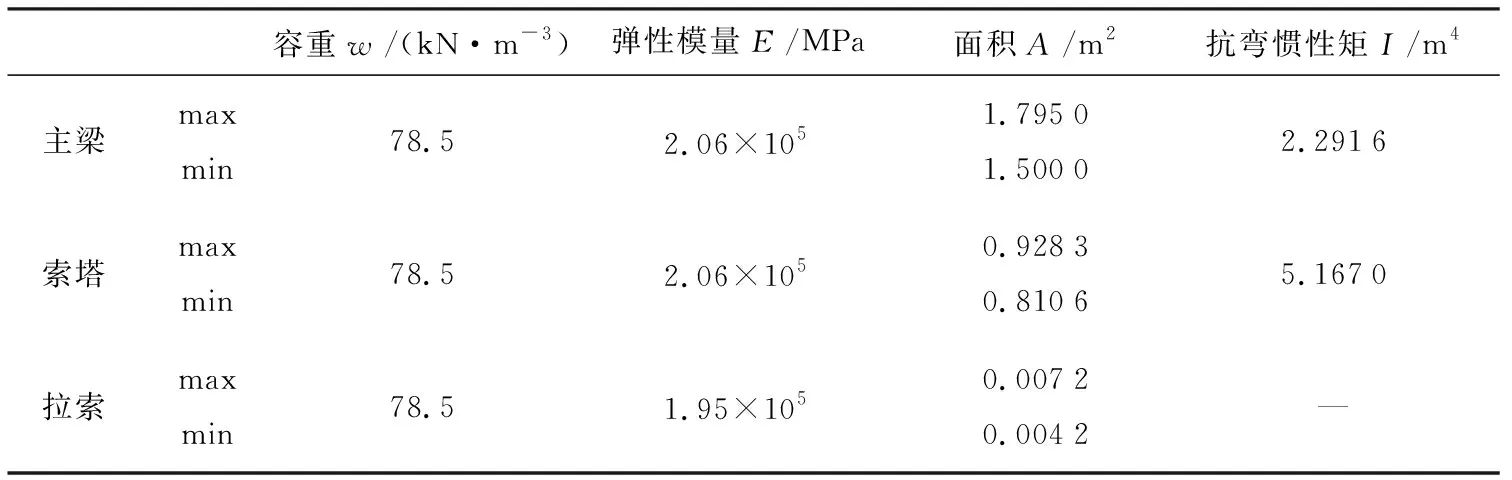
表1 模型計算參數

2.3 計算結果

原設計圖轉體前懸臂狀態、由原設計圖成橋狀態反演得到轉體前懸臂狀態以及本文優化后的轉體前懸臂狀態的主梁線型與索力對比，如圖5所示.

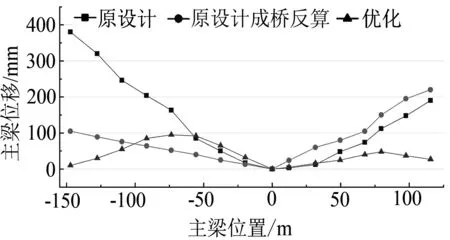
(a) 主梁節點豎向位移

由圖5(a)可知，與原設計轉體狀態、原設計成橋狀態反算得到的轉體狀態相比，優化得到的主梁節點豎向位移更小，且有一定的安全儲備；主梁線型分布均勻，位移最大差值Δμmax﹤100 mm；懸臂端設計高程誤差更小，分別為17.3和26.5 mm，利于轉體結束時主梁懸臂端與臨時轉體輔助墩的精確對接以及后續的合龍施工.由圖5(b)可知，與原設計轉體狀態、原設計成橋狀態反算得到的轉體狀態相比，優化得到的斜拉索內力均勻性下降，但索力均勻性只有在成橋運營期間有要求，在施工階段沒有必要.在整個施工過程中，斜拉索內力都在應力允許范圍以內，且具有足夠的安全儲備.

此外，在二次調整索力之前的整個施工過程中，主梁、索塔的最大節點位移μmax﹤150 mm，υmax﹤122 mm，結構構件的應力狀態都在可控范圍以內，能夠保證安全施工.

3 結論

基于影響矩陣理論，運用Midas/Civil 2019有限元數值分析軟件，通過對比分析原設計圖轉體過程懸臂狀態、由原設計圖成橋狀態反演得到轉體過程懸臂狀態以及本文方法優化得到轉體過程懸臂狀態的主梁線型與索力，得出如下結論：

(1)斜拉橋的平面轉體施工過程是整個施工過程的關鍵，對該轉體前懸臂狀態進行獨立的優化分析是完全必要的.采用影響矩陣與數學優化函數能夠綜合考慮轉體法施工的具體限制因素，實現多目標的結構狀態優化；

(2)優化得到的轉體前懸臂狀態主梁線型更加平順；由該結構狀態控制的斜拉索張拉、主梁逐步脫離支架過程安全、可控；懸臂端設計高程誤差更小，利于轉體精確定位；

(3)優化得到的轉體前懸臂狀態斜拉索內力都在應力允許范圍以內，且具有足夠的安全儲備，相鄰斜拉索的索力值均勻性較優化之前下降，但在短期的施工階段是可以接受的.