加權譜比法Q值估計

楊登鋒 劉 軍 吳 靜 張衛衛 白海軍

(中海石油(中國)有限公司深圳分公司研究院，廣東深圳 518000)

0 引言

品質因子Q值是描述地下介質吸收衰減的重要物理參數。可靠準確地估計出Q值，通過反Q濾波和Q偏移能提高地震資料分辨率[1-5]。此外，Q值還與儲層孔隙度、裂縫發育程度和含流體性質等因素有關，因此Q值也可應用于儲層預測、油藏描述和流體檢測[6-8]。總之，準確地估計Q值在油氣勘探開發中具有重要意義。

為了準確地描述地層的吸收衰減特性，大量的Q值估計方法被提出，如解析信號法[9-10]、譜比法[11]、質心頻移法[12-14]、峰值頻率法[15]、基于衰減和補償的Q值分析方法[16]等。這些方法都有各自的適用條件和優缺點[11]。譜比法是現今很常用的Q值估計方法之一[17-18]，它是通過線性擬合對數譜比值與頻率之間的線性關系估計Q值，具有較高的理論計算精度，但當地震數據存在噪聲時，其穩定性隨噪聲的增強而迅速降低，且Q值估計結果依賴所選取的計算頻段[19-20]。為此，不少學者提出了相應的改進方法：曹思遠等[21]提出對數譜根式法Q值反演，其精度和抗噪性都有所提高； Wang等[22]提出了對數譜面積差法，相較于傳統譜比法增強了算法的穩定性； 劉國昌等通過引入整形正則化算子穩定求解不同時刻的頻譜比值[23]，并通過線性擬合估計出Q值[24]，提高了Q值估計的穩定性； 馮瑋等[25]提出在頻率域和時間域通過匹配方法求取Q值，該方法避免了譜比法中的譜除及線性擬合過程，同時也省去在頻率域估計功率譜的環節，并將時變相位包含的吸收衰減信息加入Q值估計中，有效地提高了Q值估計的抗噪性和精度。郭銳等[26]提出改進的Capon2DQ值估計方法，與常規譜比法相比，改進方法對高頻噪聲不敏感，兼具壓制子波干涉的能力。Blias[27]采用最優化方法對傳統譜比法作了改進，可更穩定地估計Q值； Sangwan等[28]通過非線性反演振幅譜比方法獲得了穩定的Q值估計結果。

迄今為止，力求提高譜比法Q值估算的穩定性依然是Q值反演估算的重要研究內容。基于譜比法Q值估計原理基礎，并參考加權質心頻移法[29]的思路，本文提出加權譜比法Q值估計新方法。該方法首先以高斯函數對對數譜比值進行加權處理，然后借助最小二乘線性擬合實現Q值估計。模型分析和VSP實測數據應用結果表明，該方法不僅具有良好的Q估值穩定性，而且能夠降低對頻段選取的依賴性。

1 基本原理

當地震波在地層中傳播時，由于地層的非完全彈性，地震波會產生衰減。衰減過程可用Futterman常Q模型[30]表示

(1)

式中：A0(f)為震源子波振幅，其中f為頻率；A(f)為接收子波振幅譜； Δt為旅行時；C表示散射衰減，在整個地震頻段內與頻率無關，包括幾何擴散、反射、透射等。

將A(f)與A0(f)相除并取對數，據式(1)可得

(2)

式(2)是關于頻率的線性函數，可改寫為

L(f)=kf+b

(3)

基于式(3)，在一定頻段范圍內做最小二乘線性擬合，目標函數如下

(4)

式中m為頻點個數。由該式即可得到直線斜率k。

根據斜率與Q值關系，得到Q值估計公式

(5)

上述估計Q值方法稱為譜比法。

地震數據中含噪聲時，譜比法穩定性差且估計結果依賴所選取頻段。這是由于譜比法在做最小二乘法擬合直線時采用的是等權重法，導致其擬合結果受低頻和高頻區異常值影響較大。為了提高譜比法的穩定性，降低其對頻段選取的依賴性，本文提出了加權譜比法估計Q值。

由于子波振幅譜低頻成分和高頻成分有效信號強度弱，更容易受噪聲干擾，使遠離主頻成分的振幅譜信噪比較低[14，24]。為了降低低信噪比信號的影響，Li等[29]提出加權質心頻移法提高質心頻移法估計Q值的穩定性。此方法選取高斯函數作為權重因子，其中高斯函數對應的峰值頻率和方差分別為震源子波的質心頻率和方差，這樣在計算過程中可實現高信噪比信號的參與權重大、低信噪比信號的參與權重小。參考加權質心頻移法思路，本文提出的加權譜比法在擬合直線時的權重因子同樣選取高斯函數，其表達式為

(6)

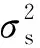
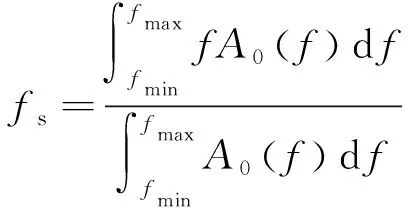
(7)

(8)

式中fmax、fmin分別為頻率上限、下限。基于式(3)做最小二乘線性擬合時，加上權重因子，目標函數為

(9)

取?J/?k=0和?J/?b=0，可得下列方程組

(10)

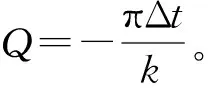
上述估計Q值的方法稱為加權譜比法。

2 模型測試

首先選用無噪聲合成衰減地震記錄(圖1)驗證所提方法的有效性。在合成記錄中震源子波分別選用主頻為45Hz的Ricker子波和可控震源Klauder子波[31](低截頻和高截頻分別為5Hz和85Hz)，置于合成記錄150ms處； 在頻率域計算得到衰減后的接收子波頻譜，然后反傅里葉變換得到時間域的衰減接收子波，位于合成記錄450ms處。合成記錄從左到右Q值分別為25、50、100、200。基于圖1合成地震記錄，分別利用常規譜比法和加權譜比法做Q值估計。加權譜比法選取5～100Hz頻段計算震源子波的質心頻率和方差，用于構建高斯函數權重因子。在估計Q值時，兩種方法頻段同樣選為5～100Hz，估計的Q值相對誤差如圖2所示。

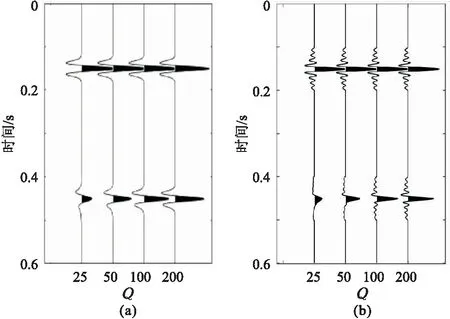
圖1 含衰減的Ricker子波(a)和Klauder子波(b)合成地震記錄

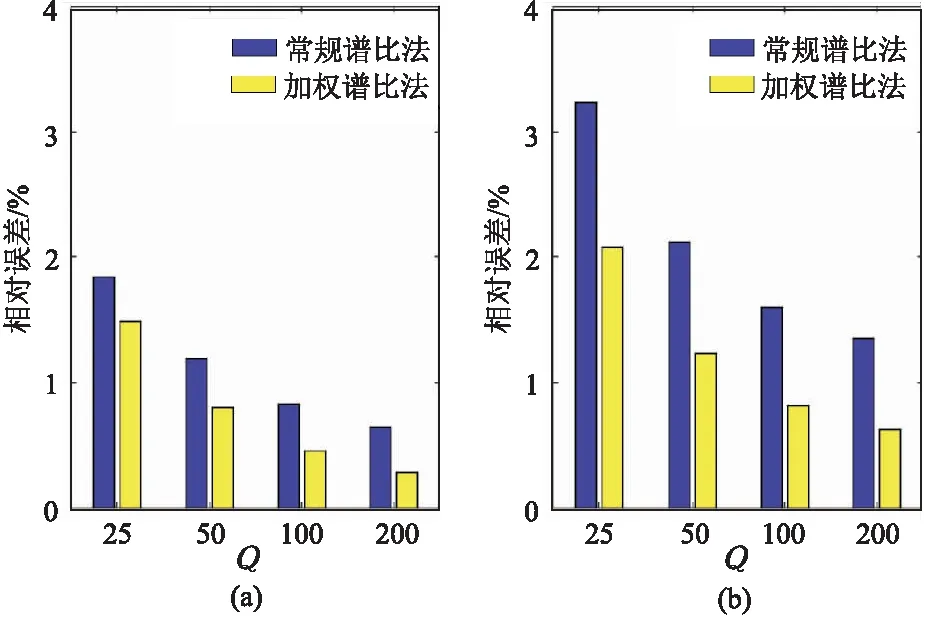
圖2 Ricker子波(a)和Klauder子波(b)的常規譜比法和加權譜比法Q值估計相對誤差

從圖2可看出，不同子波在無噪聲時兩種方法估計結果相對誤差都小于4%，表明兩種方法都能較精確地估算Q值。此外，在不同Q值下加權譜比法相對誤差都小于常規譜比法。測試結果表明：相較于常規譜比法，加權譜比法Q值精度更高。

由于實際地震資料中存在噪聲，會影響Q值估計的穩定性。可利用含隨機噪聲合成地震數據對比分析常規譜比法與加權譜比法對噪聲的敏感程度。每一道中加入10%隨機噪聲(震源子波最大振幅值10%)，如圖3所示。

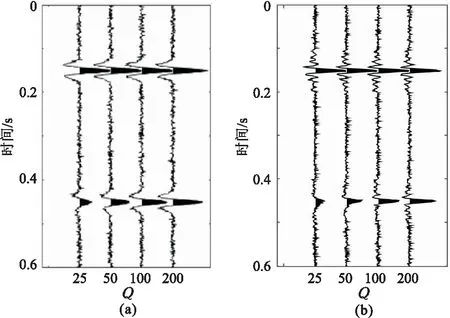
圖3 含10%隨機噪聲衰減的Ricker子波(a)和Klauder子波(b)地震記錄

分別以圖3a和圖3b第3道(Q=100)為例，選取頻段5～100Hz，對比常規譜比法和加權譜比法Q值估計結果。繪出常規譜比法和加權譜比法擬合直線，并疊加理論曲線(Q=100)與實際對數譜比曲線(圖4)。從圖4a(震源子波對應Ricker子波)和圖4b(對應Klauder子波)中都可看出：實際對數譜比曲線(綠線)在噪聲影響下存在擾動，且在低頻端和高頻端擾動表現得更劇烈，與無噪聲情形的譜比曲線(黑線)差異較大。基于實際對數譜比曲線，常規譜比法和加權譜比法擬合的直線分別用藍線和紅線表示； 可發現加權譜比法擬合直線與理論直線更接近，常規譜比法擬合結果與理論直線差異明顯。

通過擬合直線的斜率估計Q值。基于Ricker子波(圖4a)的常規譜比法估計的Q值為121，加權譜比法估計的Q值為104； 基于Klauder子波(圖4b)的常規譜比法估計的Q值為163，加權譜比法估計的Q值為102。在不同子波類型下，加權譜比法結果都更接近理論值100。該測試結果表明，加權譜比法估計結果更接近真值，Q值估計穩定性明顯好于常規譜比法，且不受子波形態影響。

隨機噪聲對地震數據的干擾具有隨機性，通過多次試驗，對常規譜比法與加權譜比法進行統計對比分析。基于圖3含噪聲衰減地震記錄，同樣選取5～100Hz頻段，進行2000次獨立試驗。每次試驗重新生成隨機噪聲，將重新生成的隨機噪聲按震源子波最大振幅值10%的比例加入無噪聲衰減地震記錄中，從中估計Q值，從而得到2000個Q值估計結果，然后對其進行統計分析。

圖5和圖6分別為基于圖3a中Ricker子波和圖3b中Klauder子波估計的Q值概率分布圖。從該概率分布圖的形態看，加權譜比法聚焦性都明顯好于常規譜比法，且其峰值對應的Q值更接近理論值。表1為統計的均值μ和標準差σ，可見加權譜比法的均值更接近于理論值，標準差都更小。同時，從概率分布圖和均值、標準差統計表中都可看出基于Ricker子波的概率分布特征與基于Klauder子波概率分布特征相似。該統計分析結果表明加權譜比法抗噪性更好，穩定性更強，同樣適用于振幅譜為“門”形的地震子波。

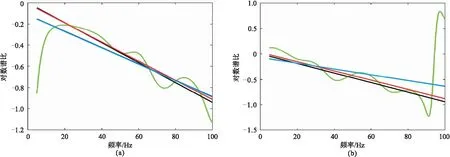
圖4 Ricker子波(a)和Klauder子波(b)的對數譜比曲線及不同方法擬合的直線綠色：實際對數譜比曲線； 黑色：理論Q值(Q=100)對應直線； 藍色：常規譜比法擬合直線； 紅色：加權譜比法擬合直線

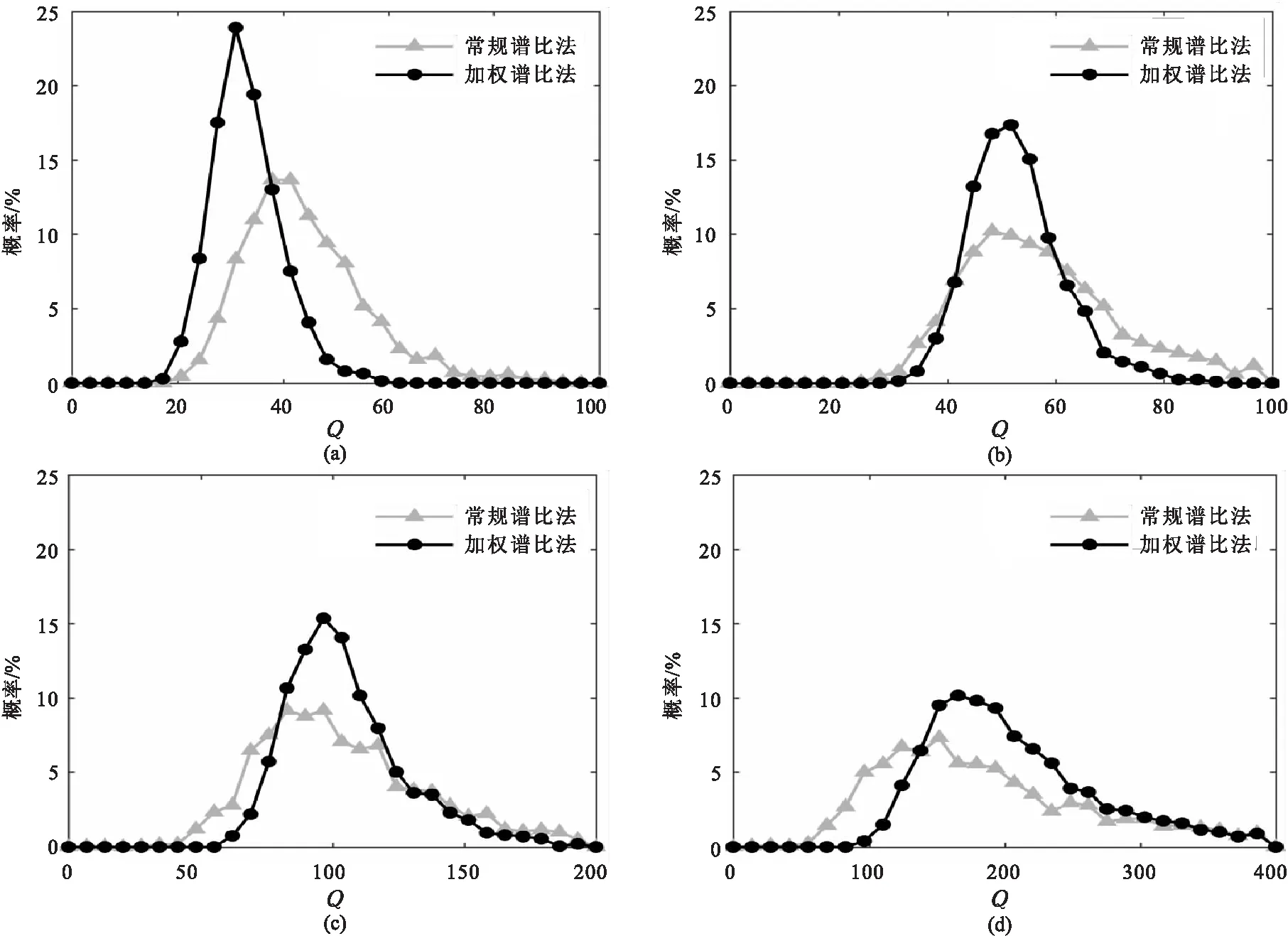
圖5 基于Ricker子波估計的Q值概率分布(a)Q=25； (b)Q=50； (c)Q=100； (d)Q=200

為分析不同等級噪聲對常規譜比法和加權譜比法的影響，做了進一步測試。以圖1a和圖1b中第3道(Q=100)為例，加入不同等級的隨機噪聲，噪聲占比的變化范圍是0～21%。在5～100Hz頻段內，進行2000次獨立試驗，在不同子波條件下兩種方法估計的均值和標準差分別如圖7和圖8所示。從均值圖(圖7a、圖8a)上可看出，噪聲占比越低，Q值估計結果越精確。如在噪聲占比為0時，兩種方法估計結果都接近于理論值，對應的標準差為0。當噪聲占比達到21%時，圖7中常規譜比法和加權譜比法估計的均值(圖7a)分別為169和120； 圖8中常規譜比法的均值(圖8a)達到146，而和加權譜比法只有116。在不同等級噪聲下，常規譜比法所得Q估值與理論值的差異都大于加權譜比法； 且隨著噪聲逐漸增大，兩種方法均值和標準差曲線斜率都逐漸增大，但常規譜比法斜率變化速率明顯大于加權譜比法。也就是說，常規譜比法對噪聲更敏感，即加權譜比法的抗噪聲能力更強。

另外，由于實際地震資料普遍存在噪聲，使Q估值的穩定性依賴于所選取頻段。同樣基于圖3a和圖3b中第3道(Q=100)含噪衰減地震記錄，分別應用兩種方法在不同頻段內估計Q值，計算其相對誤差(圖9和圖10)。將坐標橫軸和縱軸對應設定為頻段下限、上限，如坐標(5，90)對應的點即表示選擇的頻段為5～90Hz時Q估值的相對誤差。從圖9a可看出，常規譜比法對頻段的選取非常敏感，尤其是頻段選取較寬時，會嚴重影響估計Q值的可靠性。如頻段上限超過104Hz時，Q估值的相對誤差大部分大于50%； 選取的頻段低截止頻率越高，誤差越大。然而，加權譜比法在選擇相應的不同頻段時，Q估值的相對誤差都較小(圖9b)。當頻段上限高達120Hz時，大部分Q估值的相對誤差不超過30%；即使選取的積分頻段為20～120Hz，其相對誤差同樣低于30%。加權譜比法的最大優勢是在選取很寬頻段時，Q估值的差異非常小，即穩定性較好。

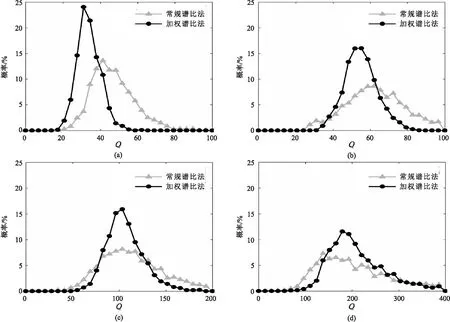
圖6 基于Klauder子波估計的Q值概率分布(a)Q=25； (b)Q=50； (c)Q=100； (d)Q=200

表1 估計Q值的均值μ及標準差σ

比較圖9與圖10，可見在不同子波條件下兩種Q值估算法表現出類似結果。該測試證實，加權譜比法對頻段的依賴性明顯弱于常規譜比法。

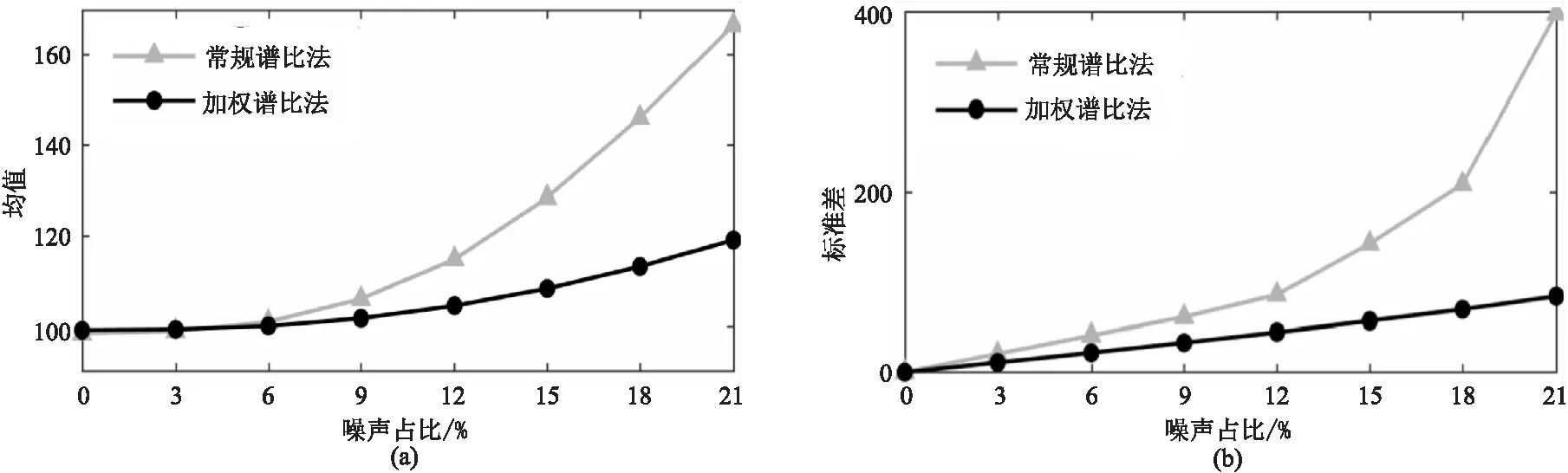
圖7 基于Ricker子波不同噪聲條件下常規譜比法與加權譜比法估計Q值的均值(a)和標準差(b)

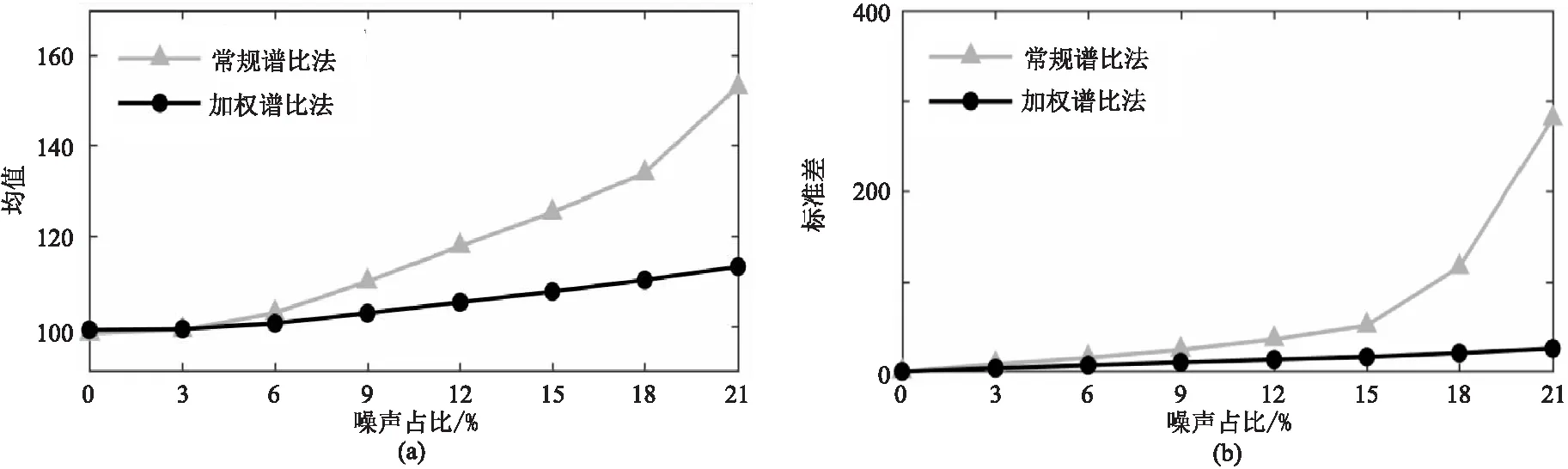
圖8 基于Klauder子波不同噪聲條件下常規譜比法與加權譜比法估計Q值的均值(a)和標準差(b)

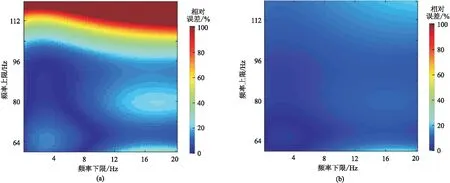
圖9 基于Ricker子波不同頻段的常規譜比法(a)和加權譜比法(b)估計Q值的相對誤差

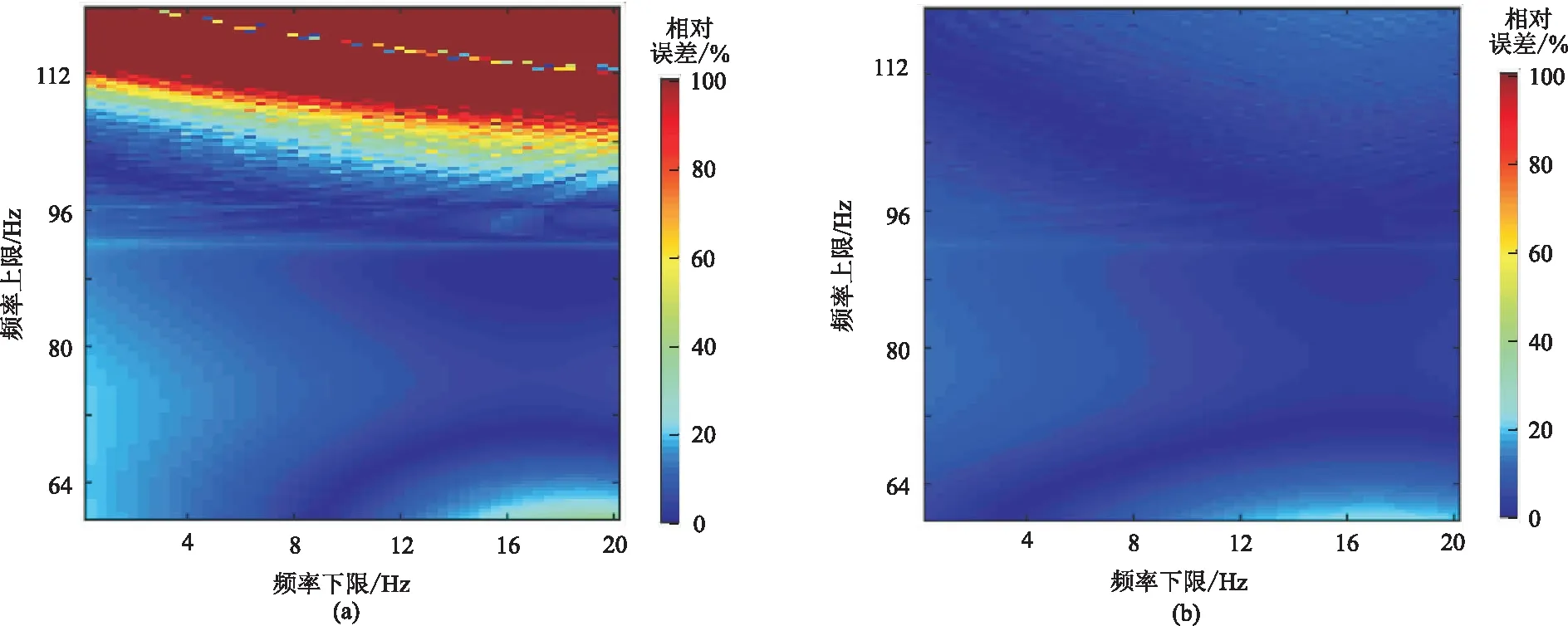
圖10 基于Klauder子波不同頻段的常規譜比法(a)和加權譜比法(b)估計Q值的相對誤差

3 實際資料應用

選用實際零偏VSP地震資料對比分析常規譜比法和加權譜比法的適用性。圖11為南海東部M油田實測零井源距VSP記錄，采用氣槍震源激發，檢波器排列放置深度為1500～2500m，道間距為20m，總共51道。對原始零井源距VSP資料做波場分離得到下行波并從中截取直達初至波(圖12a)。圖12b為通過傅里葉變換得到的初至波振幅譜。在估計Q值過程中分別選取5～100Hz和10～90Hz頻段用于對比。

圖13是在不同頻段內兩種方法估計的Q值。從該圖可看出，在相對較寬的頻段(5～100Hz)內兩種方法估計的Q值存在明顯差異，常規譜比法(淺灰線)波動明顯，穩定性較差； 在較窄頻段(10～90Hz)內兩種方法估計的Q值的差異減小。

將兩種方法在不同頻段內估計的Q值相減，得到二者之差ΔQ(圖14)。從圖中可看出，常規譜比法在不同頻段內估計的ΔQ值差值明顯大于加權譜比法，因其Q估算值受所選取頻段范圍的影響較大； 加權譜比法在不同頻段內估計的Q值幾乎無變化，即穩定且可靠，受頻段影響較小。實際VSP資料的應用效果再次證明了加權譜比法的實用性和可靠性。

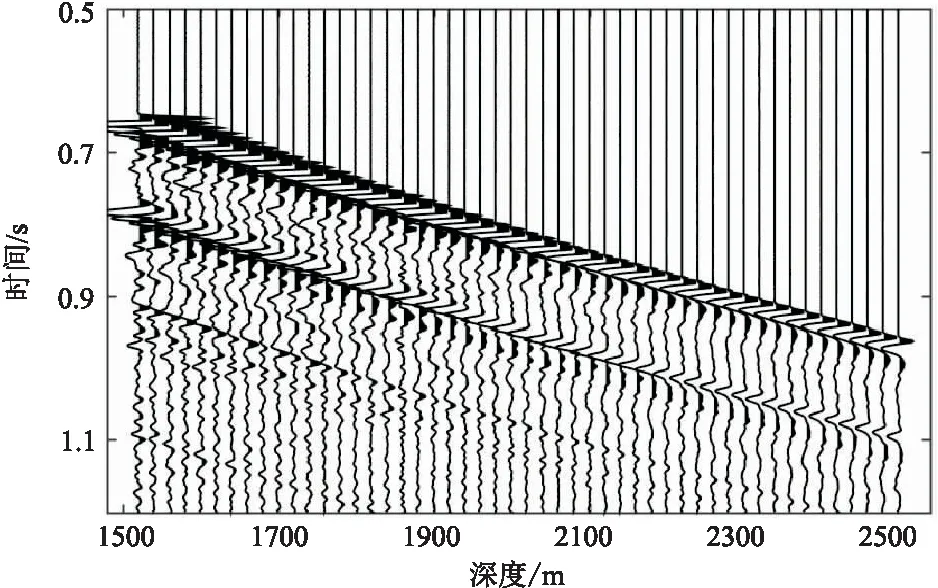
圖11 M油田實際零偏VSP地震記錄

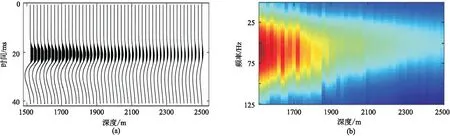
圖12 VSP下行直達波初至(a)及其振幅譜(b)

圖13 兩種方法在5～100Hz(a)、10～90Hz(b)頻段內的Q值估計結果

圖14 不同頻段內估計的ΔQ值

4 結束語

(1)加權譜比法Q值估計新方法在無噪聲干擾情況下，能更精確估計Q值，估計精度優于常規譜比法。

(2)與常規譜比法相比，加權譜比法對噪聲的敏感性減弱，對頻段選取的依賴性較低，Q值估計結果更加穩定可靠。