FRP材料動態本構模型綜述
郝仙娟, 許有純, 舒營
(1.西京學院,西安 710000;2.安徽理工大學,安徽 淮南 232001)
0 引言
纖維增強復合材料(FRP)在各個領域的應用得到頗多關注,但是FRP材料在使用期間,可能會受到不同程度的沖擊荷載作用。例如,飛機在起飛或降落過程中遭受的荷載沖擊,此沖擊如同超速運動的石塊或是碎片撞擊機身;冰雹風暴天氣中,飛機所受損害與受到物體沖擊帶來的傷害無區別。不同的沖擊荷載作用下,FRP材料不僅受到顯而易見的外部損傷,還有不可估量的內部損傷。內部損傷會嚴重影響材料的強度和剛度,還會導致材料內部裂紋延伸。
隨著經濟的快速發展和計算機技術的日益成熟,數值分析成為較多研究者的首選方法,它不僅節約資金,還可以使物體破壞過程再現,以獲取在試驗中不易獲得的相關物理量。材料的本構模型是開展數值分析的前提。在應變率作用下,復合材料的破壞形態復雜多樣,本構模型比較難以表達。為攻破這一難關,學者們紛紛開展探討。文中從細觀力學方法和宏觀唯象方法兩個方面展開敘述FRP材料動態本構模型。細觀力學常用的方法有Eshelby等效夾雜理論、自洽理論、Mori-Tanaka方法等[1-3]。
1 細觀力學方法
細觀力學[4]是從微觀角度對復合材料進行結構分析,揭示宏觀材料的有效性能。研究不同材料組合產生不同性能的原因,才能有針對性的設計出最佳的復合材料結構,滿足實際工程需求。
1.1 粘彈性本構模型
在動態破壞過程中,不會看到復合材料出現塑性變形,也不會出現跟金屬材料相似的屈服強化過程。因此,復合材料的黏彈性本構模型得到較多關注。
粘彈性本構模型[6]的統一形式是:任意時刻t粘彈性介質的應變為彈性部分和流變部分之和,即:
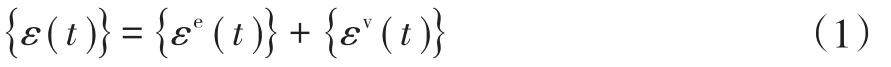

Wang等[7]用1個線彈性單元與多個Maxwell體平行連接方法,創建了復合材料粘彈性動態本構模型。該模型用于單向復合材料在高應變率作用下的力學性能研究,其中的相關參數是由不同應變率試驗數據擬合而來。
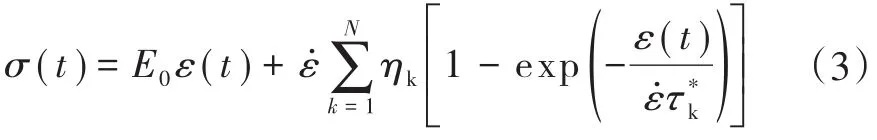
式中,E0為彈性模量通常稱為松弛時間。
Karim[8]是假設碳纖維和基體分別為線彈性材料、線性粘彈性材料,并把經典層合板理論和復合材料粘彈性動態本構模型(1個線彈性單元與多個Maxwell體平行連接)相結合,得到復合材料動態本構模型。
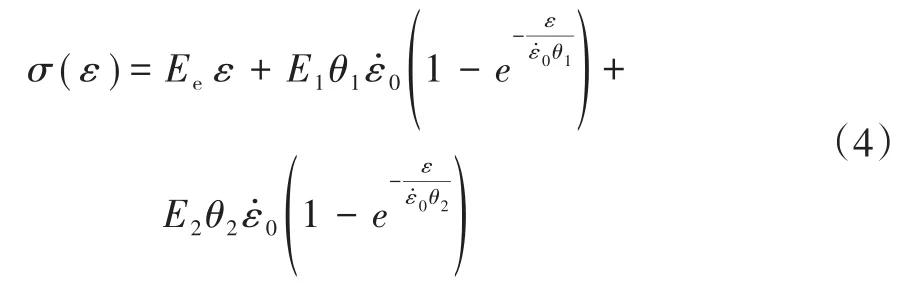
式中,Ee為平衡模量;E1和E2是與時間有關的模量;θ1和θ2是特征松弛時間;為恒定應變率。
古興瑾在 Kairm[8,9]的動態本構關系研究基礎之上,采用1個線性彈性單元與2個Maxwell體平行連接的方法,對復合材料與應變率相關的三維本構關系進行推導。
1.2 橋聯模型
橋聯模型[10-13]中的纖維組分應力和基體組分應力之間用一個矩陣來連接,它的纖維應力和基體應力是由總應力來確定的。橋聯模型可用于分析纖維增強復合材料的彈性和非彈性問題。
纖維、基體以及復合材料所滿足本構方程如式(5)所示:
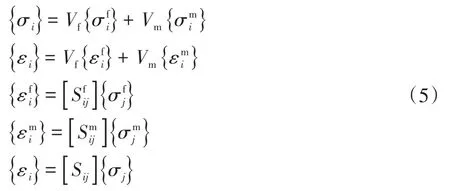

橋聯矩陣中所涉及的計算參數公式如下:
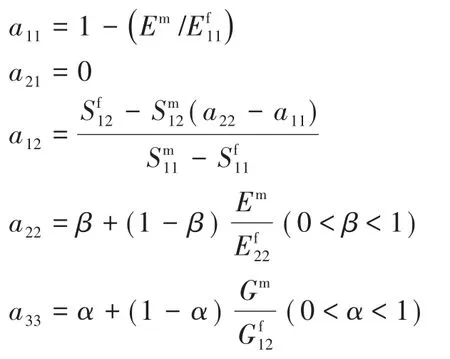
式中,稱α和β為橋聯參數,它們能通過試驗測得的橫向模量和剪切模量來調節,從而取得最佳參數值。若沒有試驗結果進行對比,α和β可在0.3~0.5和0.35~0.5之間取值。
由以上公式可以得到單向復合材料3個基本力學性能公式:
(1)纖維中的內應力為:
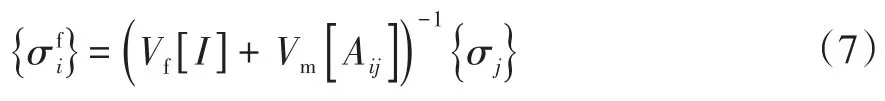
(2)基體中的內應力為:
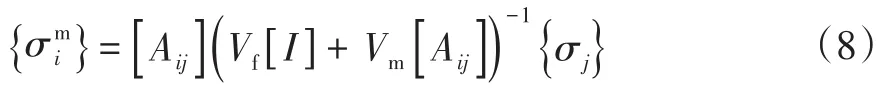
(3)單向復合材料的柔度矩陣為:

復合材料的其他一些力學參數可以根據這3個基本公式得出。由此可以導出的橋聯模型等效彈性常數:
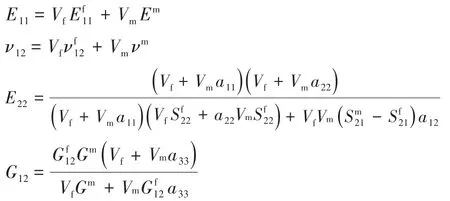
劉柳假定纖維是彈性體材料,基體是均質的各向同性材料。在動態荷載作用下,它們表現出粘彈性性質。考慮應變率的影響,把整體本構模型進行修正。CFRP材料的應變率強化效應在改進的橋聯模型中得到了大致的體現。
2 宏觀唯象方法
宏觀唯象方法[15]是用宏觀上的應力、應變對復合材料力學性質描述。形式簡單,工程應用十分方便。
2.1 正交各向異性材料本構模型
參考朱濱[16]彈性力學中關于廣義Hooke定律知識,把它和宏觀唯象理論相比,最終把正交各向異性材料本構模型用宏觀唯象方法研究。
典型的CFRP屬于正交各向異性材料,根據廣義的Hooke定律[16,17]可以知道,正交各向異性體的本構關系可以表述為:

式中,C為剛度系數矩陣,具有對稱性,可表示為:

同樣,S為柔度矩陣具有對稱性,S=C-1。
方盈盈[18]用動態增強因子修改正交各向異性材料本構模型中的柔度矩陣和剛度矩陣,得到復合材料三維動態連續損傷本構模型:

2.2 含損傷率相關本構模型
許沭華[19]在Kevlar纖維復合材料的動態壓縮試驗的基礎上,列出有關含損傷率的本構模型,并得出與應變率相關參數n的擬合關系式。
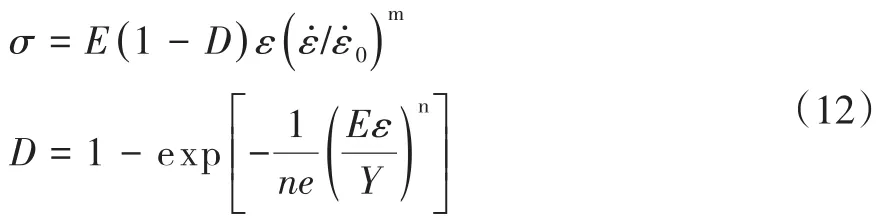
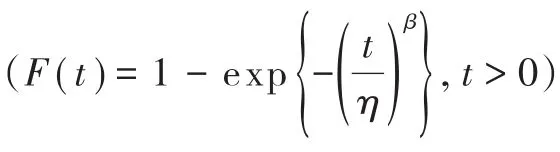
劉明爽[21]在2D-C/Si C復合材料動態壓縮試驗結果的基礎上,對彈性模量進行動態修正,建立模量與應變率的對數呈線性的關系式,并提出一種率相關的損傷本構模型。


式中,E為彈性模量;Y為屈服強;e為自然對數底數;n為曲線形狀的影響參數;m為應變率系數;Es為參考彈性模量;A為待定系數為加載應變率為參考應變率。
Salas P A和Benson D J等[22]以力學性能參數與應變率對數的關系表達式為基礎,對本構模型中的彈性模量進行修正:
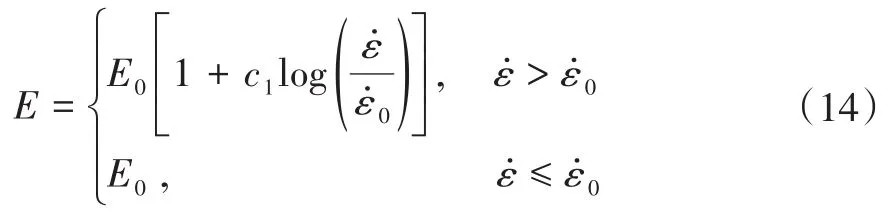
式中,c1為縮放參數(用以控制應變率)。
2.3 其他本構模型
在中等應變率作用下,材料會呈現應變率強化效應和溫度軟化效應現象。韓小平[23]在這一現象基礎上,參考金屬材料動態本構模型-Johnson-Cook模型[24-26],得出具有溫度耦合效應的復合材料率相關動態本構模型:
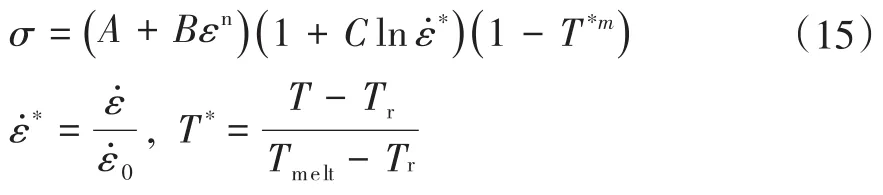
式中,ε為等效塑性應變;A、B、C為材料強度的相關參數;n為應變強化指數為無量綱變化量;為塑性等效應變率為參考應變率;m為溫度軟化指數;Tmelt為材料熔化溫度,K;Tr為參考溫度,K。
TAY等[27]得出的本構模型是一個經驗形公式。它的待定參數少,形式簡單,大致上可以描述材料的動態特性。公式中的參數是通過動態試驗獲得,其中動應力σd確定存在諸多困難,q1的物理含義尚不確切,它只能通過擬合大量實驗數據結果來獲得。

Xia和Wang等[28,29]在沖擊拉伸試驗結果和單參數的Weibull函數兩者的基礎上,提出強度的統計分布函數,與試驗結果相比較,此應力-應變曲線計算結果吻合度較高,核驗了該模型的準確性。
Harding J[30,31]等提出,應變率對單向CFRP的影響是可以忽略的。而Al-zubaidy等不認同應變率對CFRP材料性能無影響這一觀點。Al-zubaidy等[32]提出了一系列經驗性公式,用于評估不同應變率下CFRP可能的響應。該公式描述碳纖維布在不同應變率下的抗拉強度、彈性模量和破壞應變。這些方程如下:
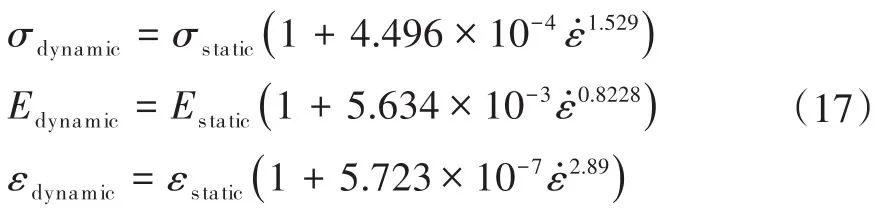
3 模型對比
從細觀力學方法角度看,在經典的處理法中,粘彈性本構模型一般是由一個線彈性單元與一個Maxwell體并聯的形式組成。但復合材料采取此經典方法需要多組線彈性單元與Maxwell體并聯的形式。Wang、Karim和古興瑾學者們采用一個線彈性單元與多個Maxwell體并聯的方式,建立復合材料粘彈性動態本構模型。采用多個Maxwell體能得到一個更精確的模型,同時計算會變得復雜。
復合材料在外荷載作用下沒有達到破壞時,橋聯模型用一個矩陣來表達組分材料內應力之間的關系。但是橋聯模型中的粘結假設是復合材料只要不破壞,纖維和基體就不發生分離和位移。理想的粘結假設沒有復合材料的應變率效應和材料的力學性能。劉柳將應變率考慮在橋聯模型之中,改進的橋聯模型大致體現了應變率強化效應。其中一些應變率參數是通過試驗數據擬合才可得出,因此修正后的橋聯模型需進一步改進。
從宏觀角度來闡明復合材料動態本構模型,大多是通過宏觀的應力應變及大量的試驗結果擬合得出復合材料的相關動態本構。這些本構模型形式相對簡單,廣泛應用。
4 結語
數值結果的真實還原度取決于復合材料動態本構模型選取的合理性。材料結構決定材料性質,在充分了解材料結構的基礎上所做的假設,得出的材料本構模型才更加合理。文中通過總結FRP動態本構得出以下結論:
(1)從細觀力學角度看,專家學者們采用一個線彈性單元與多個Maxwell體并聯的方式,建立復合材料粘彈性動態本構模型。采用的Maxwell體越多,得到的模型更精確,但是計算會變得復雜。復合材料中,組分材料界面之間的相互作用極其復雜且難處理,所以得出的動態本構模型形式復雜,在工程中難以展開應用。
(2)從宏觀角度看,大多的復合材料相關動態本構是通過宏觀的應力應變及大量的試驗結果擬合得出的。它的形式簡單,非常適合工程應用。

