猴子分桃問題的Python求解方法

王德貴

1979年著名美籍物理學家李政道教授來華講學時， 訪問了中國科技大學，會見了少年班的部分同學（科大少年班的設立，就源自李政道1974年向毛澤東、周恩來的建議）。在會見時，給少年班同學出了一道題：有五只猴子，分一堆桃子，可是怎么也平分不了。于是大家同意先去睡覺，明天再說。夜里一只猴子偷偷起來，把一個桃子扔到山下后，正好可以分成五份，它就把自己的一份藏起來，又睡覺去了。第二只猴子爬起來也扔了一個桃子，剛好分成五份，也把自己那一份收起來了。第三、第四、第五只猴子都是這樣，扔了一個也剛好可以分成五份，也把自己那一份收起來了。問一共有多少個桃子？這道題，小朋友們可能算不出來，如果我給增加一個條件，最后剩下1020個桃子，看誰能算出來？

這是個經典問題，也有很多求解方法，如純數學分析方法和各種編程語言求解方法等，但不管用什么方法，我們都可以從兩個角度來分析，一個是根據剩余數目來反推總桃子數目，另一個是從桃子總數順序推出剩余數目。下面我們就通過這兩個思路，利用Python來研究求解問題的過程和方法。

程序設計涉及的是中國電子學會等級考試四級內容。

設剩余為x個桃子，則第5個猴子來的時候看到的桃子數目為：x*5//4+1，第4個猴子未分時的數目為：（x*5//4+1）*5//4+1，……，這樣我們就可以利用遞推關系求出第1個猴子未分時的數目，即桃子的總數目（圖1）。

這個思路也可以用遞歸法求解（圖2）。

兩種方法測試結果相同（圖3）。

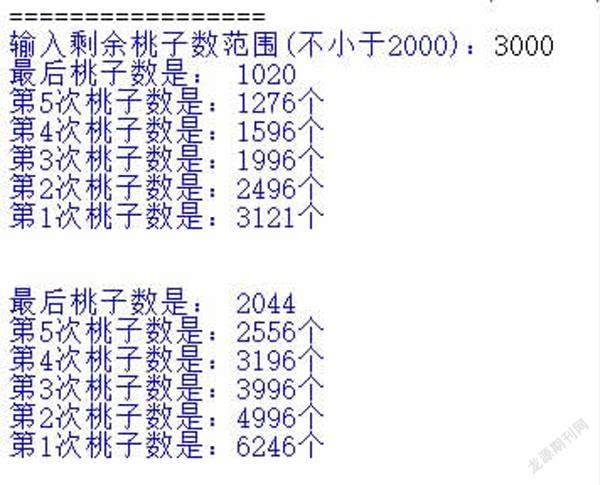
這是根據李政道教授說剩余1020個桃子，如果不知道剩余多少，是不是可以隨意輸入剩余多少個呢？我們先看程序和運行結果（圖4）。

比如隨意輸入剩余個數是2000、1200，結果如下（圖5）。

發(fā)現結果是錯誤的！桃子總數不能滿足減1后能被5整除。為什么？

因為在運算的過程中，我們是直接取整商（//）運算，而實際上沒有被整除，所以有些數值是不滿足條件的。

因此每個猴子取走桃子后，剩余數目必須是4的倍數，而每個猴子在未分桃子之前，桃子數目減1后一定能被5整除。

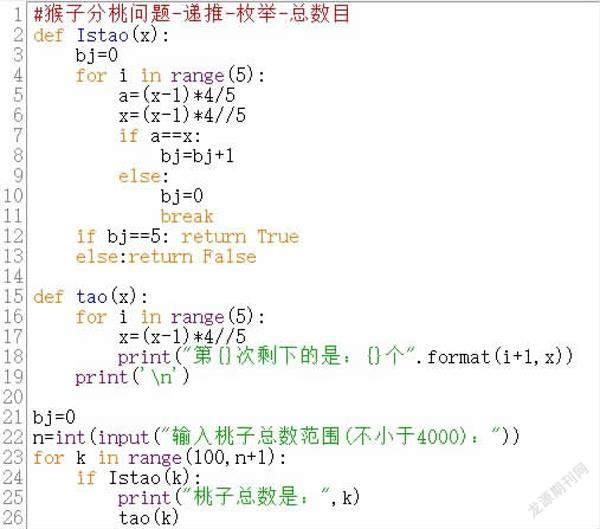
修改程序，采用枚舉法，將剩余數目在一定范圍內枚舉，并一一進行驗證，滿足條件的值才是問題的解（圖6）。

自定義兩個函數，Istao函數判斷數值是否滿足條件，tao函數是對滿足條件的數值進行求解計算，并輸出每個猴子未分之前的桃子數目。主函數是輸入范圍后，枚舉出可滿足條件的剩余數目，并輸出（圖7）。

范圍大，滿足條件的剩余數目就會增加。

我們并不知道桃子總數是多少，所以要設定一個范圍n，從前面分析可知，這個范圍應該不小于3121，否則無解。

根據前面分析，枚舉桃子總數，要滿足條件：減1后能被5整除。于是還需要先判斷是否滿足條件，再順推到最后剩余桃子數目，程序與上類似，輸入的范圍為桃子總數目，關系式變?yōu)閺目倲甸_始計算。倒推是乘以5/4，那么從總數開始計算，就是丟掉1個后的4/5（圖8）。

運行結果如下（圖9）：

遞歸方法這里不再敘述，有興趣的同學可以自己設計程序。

前面我們的分析都是假設有5只猴子，那么要是6只、7只，…n只猴子，在同樣條件下，如何求解呢？

如果其他條件不變，只是猴子數目變化了，在前例中將5個猴子的條件修改為n個猴子。看下面程序（圖10）。

運行結果如下（圖11）。

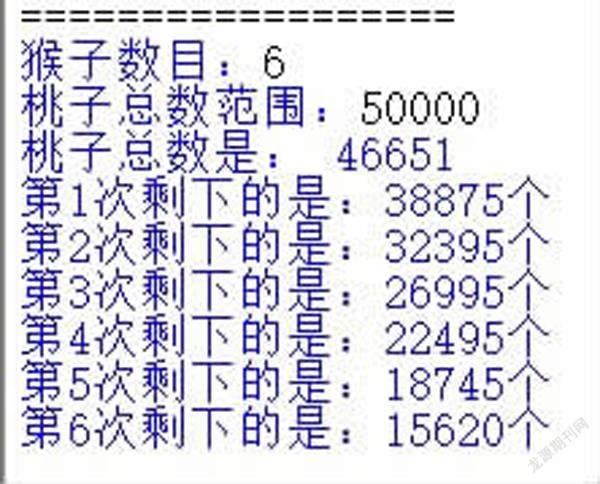
上述情況中，如果范圍輸入小了，則會無解，所以可以加個語句，提示一下（圖12）。

比如輸入8，范圍100000，則顯示無解（圖13）。

那么猴子多了，在多大范圍內才有解呢？并不好判斷！

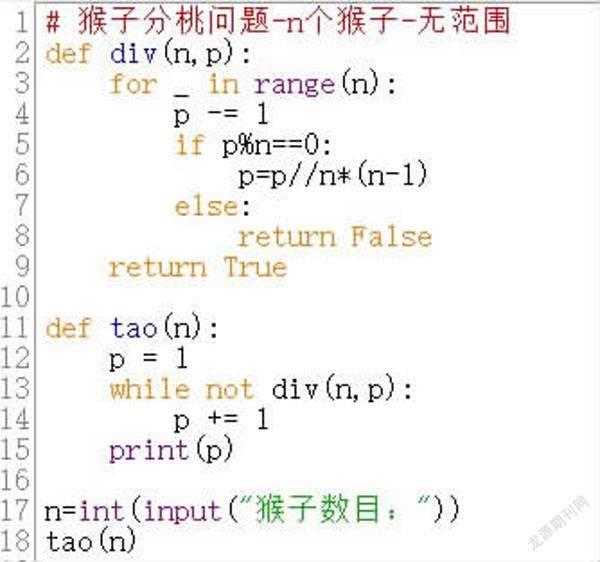
換個角度，我們可以不管什么范圍，只要沒找到滿足條件的解，就繼續(xù)查找，就不用確定數據范圍了。修改程序如下。

tao函數中，由于循環(huán)次數不確定，因而采用while循環(huán)。首先在p值增加的過程中，判斷div函數返回值，如果為假，就將p加1，否則則輸出p。

div函數是判斷桃子數目減1是否能被n整除，即被n個猴子平分，不能平分返回“假”，否則返回“真”，即是滿足條件的值（圖14）。

再次輸入8，則結果顯示如下。由此可以看到，在100000范圍內，確實無解。輸入4，結果為253（圖15）。

如果條件稍微變化一下，比如，第1個猴子發(fā)現分成5份，恰好少1個，于是他自己就拿走了少1個桃子的那份，回去睡覺了。后邊的猴子都是這樣，自己拿走了少一個桃子的那份，問，原來桃子最少有多少個？

這個問題的分析，就是每個猴子未分之前的桃子數目，加上1個，正好是5的倍數，而分完取走之后，一定是4的倍數。筆者給出一個從總數遞推的程序（圖16、圖17）。

本文從簡單方法入手，循序漸進地講解了猴子分桃問題，需要說明的是，我們只是從Python解法入手，來分析簡單的求解問題。其實在Python中還有很多方法，這里不一一介紹，有興趣的老師和同學可以自行研究一下。

本文難免有不當之處，請各位同仁、朋友斧正。