考慮輪換更新的應急物資政企協同預置儲備優化研究*

林 勇，張 立，汪貽生，肖 驊

(1.陸軍勤務學院 軍事物流系，重慶 401311；2.重慶財經學院 科研處，重慶 401320)

0 引言

應急物資政企協同預置儲備因能有效破解政府單方面預置儲備存在的供應風險高、財政負擔重、輪換更新難等問題[1-3]，被認為是高效應對災害的必然出路。有關應急物資政企協同預置儲備優化的研究已經引起學者們的關注，但研究成果主要集中在災前預置量、災后采購量和災后運輸量的聯合決策方面且研究成果較少[4-13]。同時，現有研究均未考慮預置儲備過程中的輪換更新環節，即默認預置儲備期間不會進行應急物資輪換更新。但實際輪換更新是應急物資預置儲備實踐中必不可少的環節[14-15]。鑒于此，本文在分析輪換更新環節基礎上，構建計及輪換更新費用的應急物資政企協同預置儲備優化模型，并通過數值算例驗證模型的有效性。

1 問題描述

1)應急準備階段。政府救災部門與應急物資生產企業(以下簡稱“企業”)達成協議，承諾采購不低于約定數量的應急物資，并儲備至政府下屬的儲備庫。協議同時約定，企業必須預置一定規模的庫存物資以備災后應急所需。為確保應急物資長儲常新，儲備庫和企業都需要定期對應急物資進行輪換更新。

2)應急響應階段。政府救災部門可通過應急調撥儲備庫物資和應急采購企業庫存物資2種方式進行應急救援。應急物資輪換更新涉及折舊出售和補充更新2步操作：儲備庫與企業將擬輪換的應急物資折舊出售給零售商(如大型超市)；儲備庫與企業通過協議采購以及組織生產的方式補充更新因輪換而產生的應急物資空缺。在輪換更新周期內，受外部環境等因素影響，應急物資價值通常隨儲備時間推移不斷下降，且不同類型應急物資的價值損失變化率存在差異[16]。應急物資價值與預置儲備時間函數關系如式(1)所示：

(1)

式中：C0為應急物資初生產出來時的價值，當應急物資預置儲備達到保質期T0時，其價值為0；T0為保質期，a；t為預置儲備時間，a；n為形狀參數。

2 模型構建

2.1 模型假設

為明確研究邊界，作如下假設：

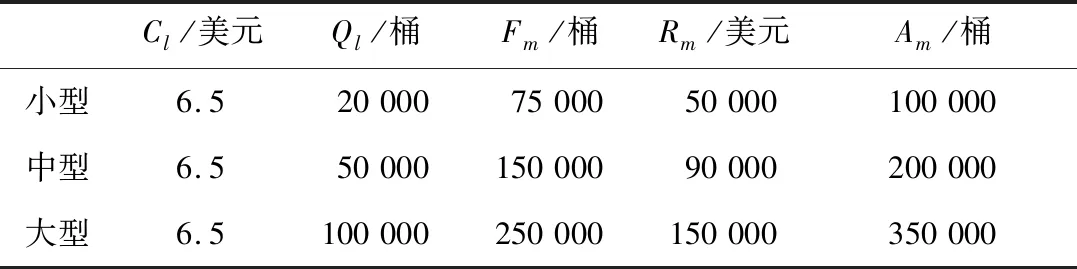
1)應急物資的保質期T0以及輪換更新周期Tg已知，且Tg

2)應急物資輪換產生的勞務費以及運輸費由零售商承擔。

3)儲備庫與企業每次輪換更新過程中補充更新的應急物資為剛生產出來的全新物資。

4)協議期T內，無災害事件發生。

2.2 數學模型

構建考慮輪換更新的應急物資政企協同預置儲備優化模型。模型目標函數如式(2)所示：

(2)

式中：f表示總成本，美元；fc為儲備庫設立成本，美元；pc為初次儲備采購成本，美元；tc為采購以及輪換更新產生的運輸成本，美元；hc為儲備庫以及企業預置應急物資產生的庫存維持成本，美元；dc為儲備庫和企業進行R次輪換更新產生的差價(折舊)補貼，美元；pcs為災后應急采購成本，美元；tcs為災后運輸成本，美元；S為災害情景集合；ωs為情景s的發生概率。各項成本如式(3)～(9)所示：

(3)

式中：Fm為m型儲備庫的設立成本，美元；xim為0～1變量，若在候選點i設立m型儲備庫，則xim為1；I為儲備庫候選點集合，i∈I；M為儲備庫大小類型，m∈M。

(4)

式中：Cl為l型企業的應急物資單位采購成本，美元；pikl為候選點i的儲備庫向候選點k的l型企業進行災前采購的應急物資量；K為企業的候選點集合k∈K；L為企業大小類型，l∈L。

(5)

式中：R為協議期內應急物資的輪換更新次數，次；TC為單位物資量、單位距離的運輸成本，美元；Hik為候選點i的儲備庫與候選點k的企業之間的距離，km。

(6)

式中：eim為候選點i的m型儲備庫應急物資儲備量；HC為單位應急物資的年庫存維持成本，美元；T為政府與企業的合同協議期限，a；gkl為候選點k的l型企業需要預置的庫存量。

(7)

式中：J為需求點集合，j∈J。

(8)

式中：ε為災后應急采購單價補償系數；rkjls為情景s下，候選點k的l型企業發售給需求點j的應急物資量。

(9)

式中：qijs為情景s下，候選點i的儲備庫調撥給需求點j的應急物資量；Hij為候選點i的儲備庫與需求點j的距離，km；Hkj為候選點k的企業與需求點j的距離，km。

模型約束條件如式(10)～(21)所示。其中，儲備庫和企業類型數量限制如式(10)～(11)所示：

(10)

(11)

最低采購量和有效采購量約束如式(12)所示：

(12)

式中：ykl為0～1變量，若選擇候選點k的l型企業，則為1；Ql為政府向l型企業進行災前采購的最低協議訂購量；B為較大的正數。儲備庫容量限制如式(13)～(14)所示：

(13)

eim≤xim·Am?i∈I，m∈M

(14)

式中：Am為m型儲備庫的最大儲備容量。災后儲備庫的調撥量不能超過其有效儲備量的限制，如式(15)所示：

(15)

式中：αis為災害情景s發生后，候選點i的儲備庫可用應急物資比例。災后采購量不能超過企業的有效預置庫存量的限制如式(16)所示：

(16)

式中：αks為災害情景s發生后候選點k的企業可用應急物資比例。企業預置庫存量不能超過企業的庫存容量限制，如式(17)所示：

gkl≤ykl·Vl?k∈K，l∈L

(17)

式中：Vl為l型企業的預置庫存最大容量。需求滿足限制如式(18)所示：

(18)

式中：Djs為情景s下需求點j的應急物資需求量。0～1決策變量約束如式(19)～(20)所示：

xim∈{0,1} ?i∈I，m∈M

(19)

ykl∈{0,1} ?k∈K，l∈L

(20)

變量的非負整數約束如式(21)所示：

pikl，gkl，qijs，rkjls，eim∈N，?i,j,k,m,l,s

(21)

式中：N為自然數集合(非負整數集)。

3 算例分析

3.1 算例設置

以美國東南部墨西哥灣颶風災害為背景[13]，選取3種代表不同價值損失變化率和輪換更新周期的應急物資為研究對象，研究計及輪換更新費用的應急物資政企協同預置儲備優化問題。假定3種代表性的應急物資分別為E1，E2，E3。E1代表方便面，設其n=0.5，Tg=0.8 a，T0=1 a；E2代表桶裝水，設其n=1，Tg=1.5 a，T0=2 a；E3代表應急燈，設其n=4，Tg=2.6 a，T0=3 a。儲備庫和企業分為大、中和小3種類型，各類型儲備庫和企業的參數見表1。其余參數設置如下：ε=0.5，TC=0.003美元，HC=0.65美元，T=3 a。

表1 與儲備庫和企業相關的模型參數設置Table 1 Setting of model parameters related to reserve warehouses and enterprises

3.2 結果分析

考慮模型為線性整數規劃模型，本文借助Anaconda平臺的Spyder集成開發環境，采用Python語言進行編碼，并調用Gurobi求解器進行求解。經計算得到以上3種應急物資對應政企協同預置儲備優化結果，見表2。

表2 3種應急物資對應的政企協同預置儲備優化結果Table 2 Optimization results of government-enterprise collaborative preset reserve corresponding to three kinds of emergency supplies

優化結果驗證本文模型的有效性，能夠對具有不同輪換更新周期的應急物資政企協同預置儲備問題進行優化求解。由表2可知，3種應急物資E1，E2，E3的輪換更新次數R分別為3，2，1次，但3種應急物資在儲備過程中需要花費的差價(折舊)補貼普遍較高，3者差價(折舊)補貼與總成本的占比分別為71.48%，69.43%，60.34%。由此可見，在應急物資政企協同預置儲備過程中，由于輪換更新環節的存在，差價(折舊)補貼是不可忽視的成本支出。另一方面，從庫存維持成本來看，盡管3種應急物資的輪換更新次數存在差異，但3者的庫存維持成本是一樣的。這是因為庫存維持成本由預置儲備量、單位應急物資的年庫存維持成本以及合同期限共同決定，與輪換更新次數無關。在本文算例中，3種應急物資的儲備期限相同，即T=3 a。

此外，由式(5)可知，在應急物資政企協同預置儲備過程中，輪換更新次數除對差價(折舊)補貼有直接影響外，還對災前運輸成本有著直接的影響。在差價(折舊)補貼成本較高的情況下，為實現總成本最小，模型優化結果勢必會對其它成本進行折中，這也是本例中3種應急物資的災前運輸成本普遍較低的主要原因。災前運輸成本較低，意味著應急物資的災前儲備采購以及補充更新主要通過與就近企業對接完成，例如對于應急物資E1而言，其災前運輸成本為0，表示各儲備庫全部通過儲備庫所在地的企業進行災前儲備采購和輪換更新過程中的補充更新。

由此可見，輪換更新次數通過影響災前運輸成本，對優化結果中儲備庫與企業的協同關系產生影響。在合同期內，對于輪換更新較為頻繁的應急物資，選擇與儲備庫較近的企業完成災前儲備采購以及輪換更新是政企雙方開展協同預置儲備的最佳方式。相反，對于輪換更新頻次不高的應急物資，可以選擇離儲備庫有一定距離的企業完成災前儲備采購與輪換更新。

4 結論

1)合同期內，無論輪換更新次數多少，應急物資政企協同預置儲備需要支出的差價(折舊)補貼普遍較高。算例中，3種應急物資因輪換更新產生的差價(折舊)補貼大于總成本的60%。

2)輪換更新次數不會影響庫存維持成本，但會影響儲備庫與企業的協同關系。合同期內，對于輪換更新較頻繁的應急物資，政府最好選擇離儲備庫較近的企業完成災前儲備采購以及輪換更新；對于輪換更新次數不多的應急物資，政府可以選擇離儲備庫有一定距離的企業完成災前儲備采購與輪換更新。