瑞利衰落信道下基于USRP的實測信號識別算法

李 佩，王 偉

（1.中國人民解放軍陸軍工程大學，江蘇 南京 210007；2.江蘇華紅科教投資集團有限公司，江蘇 南京 210007）

0 引 言

調制信號識別是信號正確解調的關鍵技術之一，在非協作通信應用中發揮了重要作用。近幾年，調制信號識別研究主要集中在基于特征提取和深度學習方面。基于特征提取的識別方法簡單方便，實時性高，但受信道環境及噪聲的影響較大；基于深度學習的識別方法具有區分能力強，識別率高等優點，但需要大量的已標注數據集支撐且計算復雜度高。文獻[1]利用八階累積量特征解決六階累積量特征參數無法識別16PSK信號的問題，實現了6種調相信號的識別。文獻[2]利用信號的瞬時特征參數和高階累積量特征參數，實現了擴頻信號和常規調制信號的識別。文獻[3]提出了一種可部署于資源受限邊緣設備上的高效智能電磁信號識別模型，該模型在運行時間、模型大小以及識別準確率上具有不同程度的提升。文獻[4]將調制信號轉換為星座圖并經過處理得到灰度圖像、增強灰度圖像以及三通道圖像，使用訓練后的卷積神經網絡對其進行識別，該方法可以有效對8種調制信號進行分類。

上述研究都是在理想高斯噪聲信道環境下進行，對衰落信道下的調制信號識別研究較少。文獻[5]提出了一種基于高階累積量和DNN模型的井下信號識別方法，在Nakagami-m衰落信道下有出色的調制識別性能。文獻[6]利用信號的四階累積量作為特征參量，研究了低信噪比下的調制識別率。文獻[7]分析了衰落信道對四階累積量的影響，并利用支持向量機的方法實現信號識別。文獻[8]針對瑞利衰落信道下調制信號識別進行研究，提出基于高階累積量比值的方法完成3種MQAM信號的識別。文獻[9]提出了一種基于高階累積量組合的調制識別方法，在瑞利信道下能夠實現OFDM信號與常見單載波信號類間識別及不同階數之間的單載波信號類內識別。文獻[5-7]使用基于高階累積量的特征參數需要已知發送信號功率的大小，從而確定其理論值并以此設置閾值進行判決分類。然而在實際非協作通信中，發送信號經過信道和噪聲的影響發生了較大的變化。接收端通過信道參數估計處理后得到的信號功率存在一定誤差，如果簡單利用信號功率歸一化后的特征參數理論值進行不同調制信號的分類，必將對識別性能造成較大影響。此外，文獻[7-9]針對平坦瑞利衰落信道展開研究，在理論分析和算法設計中均假設監測時間內接收信號經過遍歷瑞利信道。這在實際應用中將導致監測時間過長，嚴重影響調制識別的實時性。

本文針對上述文獻中存在的問題，研究了平坦瑞利衰落信道下基于高階累積量的4QAM、16QAM、32QAM和64QAM四種調制信號的識別分類。首先計算瑞利衰落信道下MQAM信號各階累積量的理論值，采用各階累積量比值的方法作為特征參數對信號進行分類，消除了發送功率和信道系數未知帶來的影響，并分析不同特征參數和符號數下的信號識別性能。仿真結果表明，聯合特征參數可以結合單特征參數的優點，達到提升整體信號識別性能的目的。本文進一步利用軟硬件結合的方式，在實際信道環境中對算法進行驗證。實驗結果表明，當信噪比為10 dB時，信號平均識別率接近90%，故具有一定的實用價值。

1 信號模型和高階累積量理論

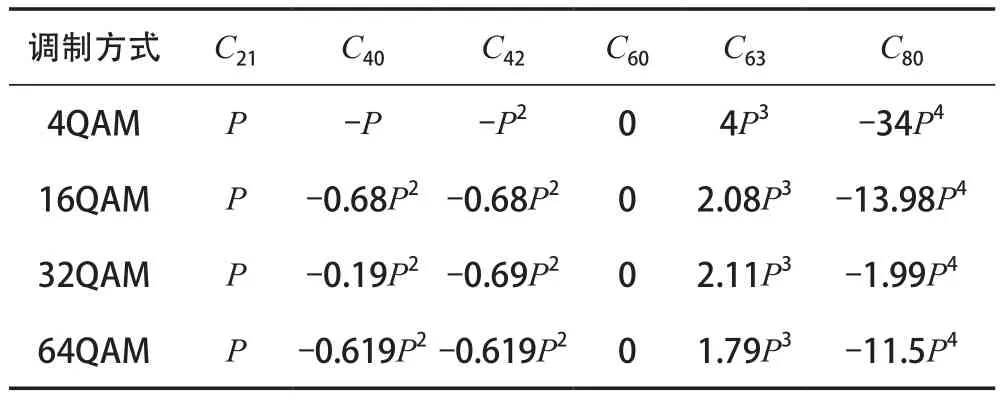
表1 4種MQAM信號的累積量理論值

在非協作通信中，由于接收信號的數據長度有限，因此只能通過有限長的數據來估計出信號的高階累積量，如式（4）所示：

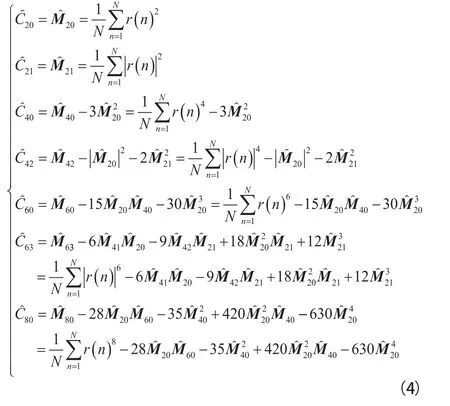
2 特征提取和決策分類

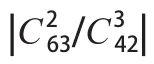
根據準靜態平坦瑞利衰落信道的傳輸特性，本文中假設接收端在一次信號監測時間內信道系數不變。在表1的基礎上，可以計算出平坦瑞利衰落信道下每個接收時間間隔內信號各階累積量的理論值。以4QAM信號為例，其二階累積量為：

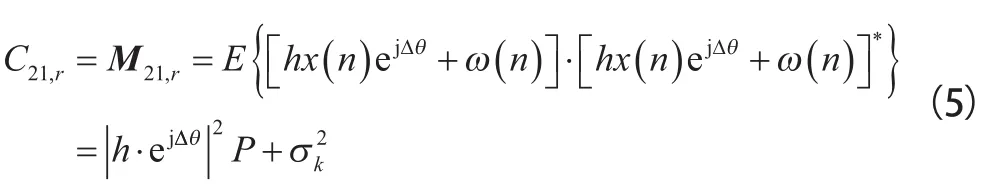
式中：表示接收信號的二階累積量；表示接收信號的二階矩；表示信道系數，服從瑞利分布；表示高斯白噪聲的方差；為信號平均功率。

2.1 單特征參數的信號識別分類

為消除信號平均功率、相位偏差Δ和未知信道系數帶來的影響，采用各階累積量比值的方法構造特征參數。根據4QAM、16QAM、32QAM和64QAM信號的各階累積量理論值，分析后構造出如下3個特征參數：

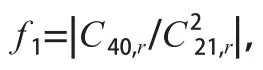
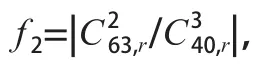
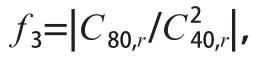
理論上，特征參數和可以完全消除高斯白噪聲的影響。實際信號處理中，由于接收信號的符號數有限，計算信號高階累積量時會存在一定的誤差。當累積量階數越高或者信噪比越低時，產生的誤差就越大。4種MQAM信號的特征參數理論值見表2所列。

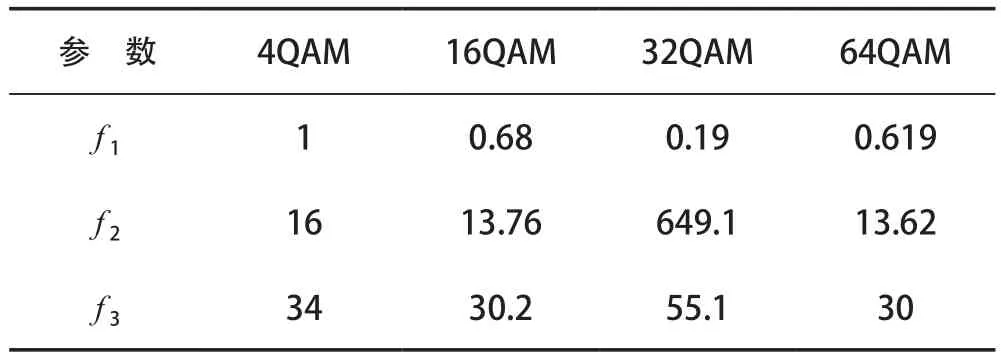
表2 4種MQAM信號的特征參數理論值

根據計算得到的特征參數理論值，閾值的確定采取相鄰特征參數求平均的方法。例如特征參數的3個閾值分別為：th=(1+0.68)/2≈0.84，th=(0.68+0.619)/2≈0.65和th=(0.619+0.19)/2≈0.41，同理可得特征參數的閾值th=332.5，th=14.9和th=13.7以及特征參數的閾值th=44.5，th=32.1和th=30.1。

2.2 聯合特征參數的信號識別分類

由于單個特征參數在識別性能上存在局限性，提出聯合特征參數的方法進行信號識別。利用特征參數和形成聯合特征參數，記為+。結合不同特征參數的優點，期望整體識別性能有所提高。聯合特征參數的閾值沿用各單特征參數確定的閾值，具體信號識別流程如圖1所示。

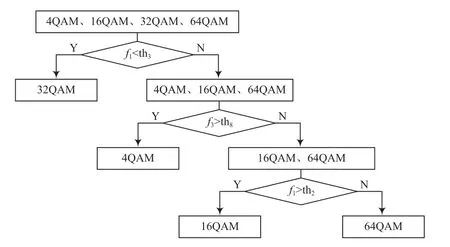
圖1 聯合特征參數f1+f3的信號識別流程

2.3 算法仿真與性能分析

采用MATLAB軟件進行仿真，隨機產生長度為的符號序列，噪聲為零均值高斯白噪聲。在平坦瑞利衰落信道下分別利用3個單特征參數和聯合特征參數+識別4種MQAM信號，分析不同特征參數的識別性能以及符號數對信號識別性能的影響。

2.4 不同特征參數的信號識別性能對比

圖2是利用不同特征參數下4種MQAM信號的平均識別性能對比圖。實驗中假設接收符號數=5 000，對各特征參數分別進行1 000次蒙特卡洛實驗。從圖中可以看出，隨著信噪比的提高，不同特征參數的信號識別性能也在提升并逐漸收斂。高信噪比條件下，特征參數以及聯合特征參數+的信號識別率超95%，明顯優于特征參數和的信號識別性能。低信噪比條件下，聯合特征參數+的信號識別性能十分接近特征參數的信號識別性能，遠優于特征參數的信號識別性能。

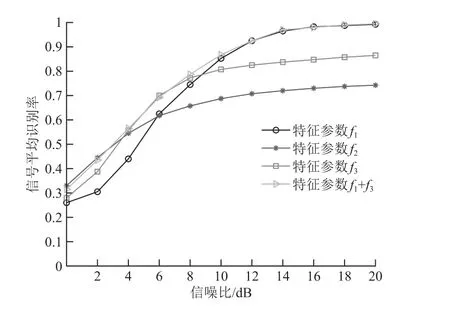
圖2 不同特征參數下4種MQAM信號的平均識別性能對比

通過分析得出結論：聯合特征參數能夠結合不同單特征參數的優點，較好地彌補單特征參數在識別性能上存在的局限性，達到提升MQAM信號平均識別性能的目的。

2.5 不同符號數下的信號識別性能對比

圖3比較了聯合特征參數+在不同符號數下的識別性能。實驗中假設接收符號數=500, 1 000, 5 000和10 000，分別進行1 000次蒙特卡洛實驗。從圖中可以看出，在相同正確識別率前提下，符號數越大，算法的信噪比適應能力越強。當符號數=5 000、信噪比大小為11 dB時，4種信號的平均識別率達90%。因此在實際應用中，可以通過增加接收符號數的方法彌補接收信號信噪比較低帶來的不足。

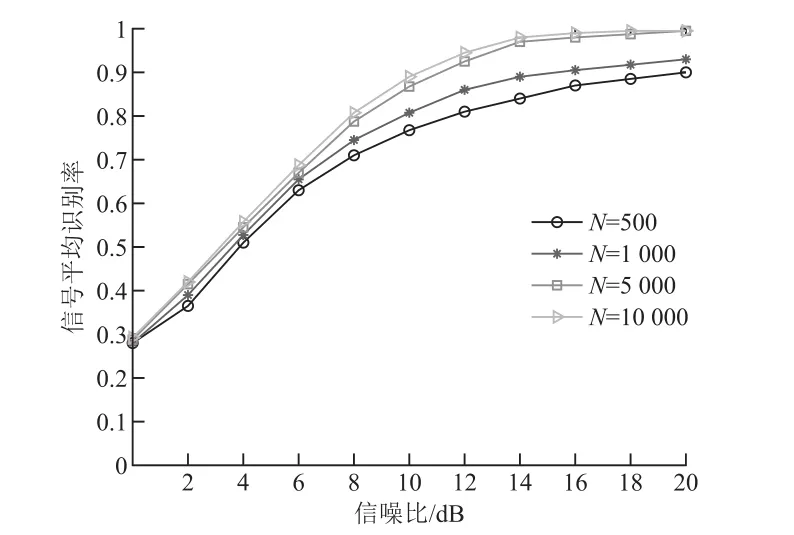
圖3 不同符號數下4種MQAM信號的平均識別性能對比

3 基于USRP的數字調制信號自動識別方案實現及性能分析

為了在真實信道環境中驗證上述方案的可行性，本文進一步利用LabVIEW平臺和軟件無線電設備NI USRP-2920搭建調制信號識別系統，實測基于高階累積量的數字調制自動識別方案的性能。識別系統實物如圖4所示。

圖4 調制信號識別系統實物

調制信號識別系統由信號源子系統、射頻信號收發子系統及特征參數提取和分類器識別子系統構成。以16QAM信號的生成為例，如圖5所示。利用Random Number.vi模塊隨機生成符號序列，設置Filter Coefficients.vi模塊中調制類型、脈沖成型濾波器以及每個符號的采樣數等參數。將符號序列、系統參數和符號速率等參數輸入Modulate QAM.vi模塊，將輸出的復基帶信號（IQ數據）上變頻到帶通信號。

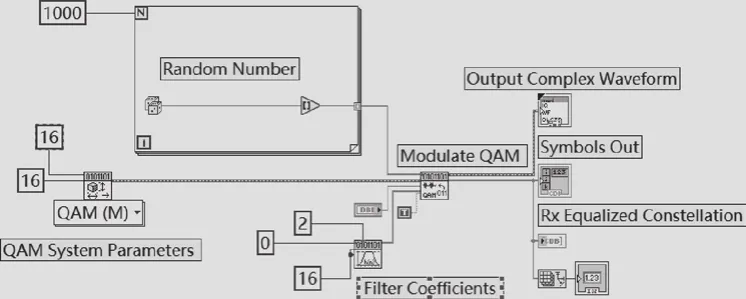
圖5 16QAM信號生成示意圖

利用LabVIEW自帶的調制工具包產生調制信號，通過兩臺USRP對生成的調制信號進行發送和接收。本實驗設置IQ速率為1 MHz，載波頻率為900 MHz，天線增益為15 dB，噪聲為加性高斯白噪聲和設備自身產生的底噪。發送端主要用到的內置函數庫有Open Tx Session.vi、Configure Signal.vi、Write Tx Data（poly）.vi和 Close Session.vi。接收端天線接收到發送端傳來的信號后，經過模數轉換、下變頻等處理得到IQ數據。接收端主要用到的內置函數庫有Open Rx Session.vi、Configure Signal.vi、Initiate.vi、Fetch Rx Data.vi和Close Session.vi，這里不再展示。

將接收到的信號數據利用本文算法進行識別，識別結果見表3所列。從表3中可以看出，基于USRP的實測信號識別性能與基于MATLAB的仿真信號識別性能非常接近。當信噪比為10 dB時，信號平均識別率接近90%，表明本算法對實際信道環境下的信號識別具有較好的適用性。

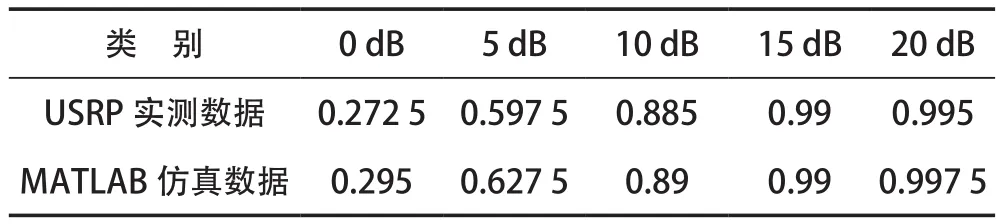
表3 基于USRP實測信號數據的識別性能

4 結 語

本文首先闡述和分析了平坦瑞利衰落信道下基于高階累積量進行調制識別的原理，利用各階累積量比值的方法構造出3個單特征參數和1個聯合特征參數，實現了4種MQAM信號的識別，并分析了不同條件下算法的識別性能。利用軟硬件結合的方式，在實際信道環境中對本文算法進行驗證。實驗結果表明，本文算法對實際信道環境下的信號識別具有較好的適用性。