基于鄰域粗糙集和帝王蝶優化的特征選擇算法

孫林，趙婧，徐久成，2，王欣雅

（1.河南師范大學 計算機與信息工程學院，河南 新鄉 453007；2.教育人工智能與個性化學習河南省重點實驗室（河南師范大學），河南 新鄉 453007）（?通信作者電子郵箱sunlin@htu.edu.cn）

基于鄰域粗糙集和帝王蝶優化的特征選擇算法

孫林1，2*，趙婧1，徐久成1，2，王欣雅1

（1.河南師范大學 計算機與信息工程學院，河南 新鄉 453007；2.教育人工智能與個性化學習河南省重點實驗室（河南師范大學），河南 新鄉 453007）（?通信作者電子郵箱sunlin@htu.edu.cn）

針對經典的帝王蝶優化（MBO）算法不能很好地處理連續型數據，以及粗糙集模型對于大規模、高維復雜的數據處理能力不足等問題，提出了基于鄰域粗糙集（NRS）和MBO的特征選擇算法。首先，將局部擾動和群體劃分策略與MBO算法結合，并構建傳輸機制以形成一種二進制MBO（BMBO）算法；其次，引入突變算子增強算法的探索能力，設計了基于突變算子的BMBO（BMBOM）算法；然后，基于NRS的鄰域度構造適應度函數，并對初始化的特征子集的適應度值進行評估并排序；最后，使用BMBOM算法通過不斷迭代搜索出最優特征子集，并設計了一種元啟發式特征選擇算法。在基準函數上評估BMBOM算法的優化性能，并在UCI數據集上評價所提出的特征選擇算法的分類能力。實驗結果表明，在5個基準函數上，BMBOM算法的最優值、最差值、平均值以及標準差明顯優于MBO和粒子群優化（PSO）算法；在UCI數據集上，與基于粗糙集的優化特征選擇算法、結合粗糙集與優化算法的特征選擇算法、結合NRS與優化算法的特征選擇算法、基于二進制灰狼優化的特征選擇算法相比，所提特征選擇算法在分類精度、所選特征數和適應度值這3個指標上表現良好，能夠選擇特征數少且分類精度高的最優特征子集。

帝王蝶優化；特征選擇；鄰域粗糙集；鄰域依賴度；二進制

0 引言

特征選擇是數據挖掘與機器學習領域中一個必不可少的數據預處理步驟［1-2］。特征選擇一般分為啟發式和窮舉式搜索兩種策略。當使用窮舉式搜索對特征數非常大的數據集進行特征選擇時，將所有特征子集列出是不現實的。為避免這一問題，許多研究者轉向研究啟發式搜索策略，如元啟發式算法。當前，已經有許多學者結合元啟發式算法解決特征選擇優化問題，例如：Hu等［3］提出了一種二進制灰狼算法并應用于特征選擇；Tubishat等［4］基于對立學習的樽海鞘群算法設計了一種局部搜索的特征選擇算法。因而，元啟發式特征選擇是目前流行的數據分類策略。

粗糙集理論是特征選擇的一種有效數學工具［5-6］。盡管粗糙集模型具有能夠去除不相關、冗余的特征，并保留原始特征的特性，但也是一種NP-Hard問題，很難找到最優解，而這正好被元啟發式算法彌補。Zaimoglu等［7］提出了基于粗糙集和拔河優化算法的特征選擇策略；Huda等［8］構建了基于粒子群優化和粗糙集的特征選擇算法；Tawhid等［9］提出了基于粗糙集和二進制鯨魚優化的特征選擇算法；Wang等［10］運用量子對蝗蟲優化算法進行改進，設計了基于互信息和粗糙集的動態種群量子二進制蝗蟲優化算法；Abd等［11］考慮到還原集中特征的數量和分類質量，將布谷鳥搜索結合粗糙集理論來構建適應度函數，提出了基于粗糙集的布谷鳥搜索算法。但是，上述基于粗糙集的特征選擇算法僅適用于符號型數據，若需要處理連續型數據，則必須進行離散化處理，這將不可避免地丟失一些重要信息［12］。為了解決這個問題，研究人員對粗糙集理論進行擴展研究，提出了鄰域粗糙集（Neighborhood Rough Set， NRS）模型、模糊粗糙集、公差近似模型等［13］。鄰域粗糙集不僅可以處理連續型數據，而且也能處理符號型和數值型的混合數據［14］。Zou等［12］通過引入自適應函數來控制人工魚的視覺和步長，結合魚群算法和鄰域粗糙集理論構建特征選擇算法。基于鄰域粗糙集的特征選擇旨在從鄰域決策系統中獲取最優/最小的特征子集［15］。截至目前，將鄰域粗糙集與群智能優化算法結合是數據挖掘領域中特征選擇的最重要的研究方向之一。

群智能優化算法是受生物群體間的智能協作過程啟發而設計的一類算法，具有實現容易、并行性好、連續和離散區間問題適應性強等優點，已經成為當前各類優化問題尤其是組合問題的求解方法［16］。受美國帝王蝶遷徙行為的啟發，Wang等［17］提出了帝王蝶優化（Monarch Butterfly Optimization， MBO）算法。該算法模擬帝王蝶利用兩個算子進行種群更新的行為，具有計算簡單、參數較少、收斂迅速、易于程序實現等優點，于是該算法在許多領域得到了廣泛的應用，例如：Dorgham等［18］采用MBO算法尋找最優閾值，使用質量結構相似指數矩陣評價分割后的圖像精度，提高圖像分割性能。Soltani等［19］開發了一種基于MBO算法高效的神經網絡模擬系統。截止到目前，利用MBO算法解決特征選擇優化問題的應用研究較少。孫林等［20］基于柯西變異的差分自適應MBO算法，結合K近鄰分類器提出了特征選擇算法。但是該算法仍存在一些問題：不能處理連續型數據，可搜索位置有限，容易陷入局部最優等。

為彌補這些局限性，利用鄰域粗糙集模型既能分析連續型數據，又能處理符號與數值的混合型數據的優勢，且二進制算子比連續算子具有更強的擬合性的特點，提出了基于鄰域粗糙集和帝王蝶優化的特征選擇算法。首先，為了使帝王蝶個體在尋找最優解時有更強的搜索能力，以避免過早陷入局部最優，在MBO算法上加入局部擾動，并結合群體劃分策略，在到目前為止找到的最優解的位置生成了解的二進制形式，構造出二進制MBO（Binary MBO， BMBO）算法；且為了進一步增強BMBO算法的搜索能力，引入突變算子增強探測階段，設計了基于突變算子的BMBO（BMBO based on Mutation operator， BMBOM）算法。然后，使用鄰域粗糙集的鄰域依賴度和所選特征子集的加權值構造新的適應度函數，對選出的特征子集進行評估并排序。最后，結合新的適應度函數，設計了基于鄰域粗糙集與BMBOM的特征選擇算法（Feature Selection algorithm based on Neighborhood rough set and BMBOM， FSNB），尋找最優特征子集使其在優化問題空間中具有更強的搜索能力，有效獲取最優/最小特征子集。在6個基準函數和14個UCI數據集上的實驗結果表明，本文算法能夠選擇分類精度較高且數量規模較小的特征子集。

1 基礎知識

1.1 鄰域粗糙集

1.2 帝王蝶優化算法

將帝王蝶優化（MBO）算法用于解決全局優化問題，性能優于其他先進的典型優化算法［17］。MBO算法搜索過程由兩種機制主導：遷移算子和調整算子，具體流程如算法1所示。

算法1 MBO算法。

輸入 初始化所有參數，適應度函數f（x），群體的規模N，空間維度D，最大迭代次數T；

輸出 最優帝王蝶個體的位置及相應的適應度值。

1） While 不滿足最大迭代或停止條件 do

2）計算適應度值并排序，找到最優帝王蝶位置和其對應的適應度值；

11） else

14） end if

15） end for

16） end for

21） else

27） end if

28） end if

29） end for

30） end for

31）將新生成的子種群合并為1個整體種群；

33） End while

2 本文特征選擇算法

2.1 改進的MBO算法

一般來說，MBO算法能找到全局最優解，但在某些時候，它可能會陷入局部最優解。在調整算子中，每只帝王蝶的步長是由dx和a決定，通過Lévy飛行完全識別搜索過程，但不能根據實際搜索情況進行調節，當步長過大時，MBO算法無法獲得最優解。為了使步長向著最好的帝王蝶去改變，嘗試擴大步長參數a的調節范圍，進行局部擾動，以幫助MBO算法跳出局部最優解。因此將步長參數a改進為：

其中：Smax表示帝王蝶的最大步長；t表示當前迭代次數；tmax表示最大迭代次數；m表示步長參數a的調整因子，隨著迭代次數的改變而改變。

接下來，對帝王蝶群體實施群體劃分策略。設當前的帝王蝶群體為N，利用適應度函數計算群體中各個帝王蝶的適應度值Fit，并得到N中最佳適應度值Fitbest和最差適應度值Fitworst。利用分別計算帝王蝶個體i和最優個體的適應度差值di，best以及和最差個體的適應度差值di，worst。若di，best和di，worst滿足，則帝王蝶個體i被劃分到精英子群中，并直接保留到下一次迭代中；否則被劃分到普通子群中，繼續迭代更新。

依據上述思路改進MBO算法，獲取分類結果，然后構建傳輸機制獲得二進制表示：

結合MBO算法和式（11），本文構建二進制MBO（BMBO）算法。為了使解決方案朝著目前為止最佳的解決方案演化，可以通過適當的突變率對普通子群中的帝王蝶個體進行局部搜索來進行突變，從而生成新的解決方案。為了避免過早收斂，可以使用具有適當突變率的突變算子來增強算法的多樣性，其中突變率是控制突變算子的關鍵因素［21］。過高的突變率會增加在搜索空間中搜索更多區域的概率，從而阻止種群收斂到任何最優解；太小的突變率可能導致過早收斂，降低局部最優而不是全局最優。因而，使用的突變率r3表示為：

其中tmax表示最大迭代次數。根據迭代次數i，參數r3從0.9線性遞減到0。于是，利用突變率r3代替式（11）中的r2，形成突變算子增強搜索能力，進而設計BMBOM算法。

2.2 適應度函數

在特征選擇的過程中，讓每個帝王蝶分頭并行地尋找最優特征子集，結合鄰域依賴度與特征子集長度的加權值，構造新的適應度函數，并將其作為啟發式信息引導算法進行迭代尋優。由此，基于鄰域依賴度的適應度函數描述如下。

其中：|B|為所選特征子集的長度；|C|為特征總個數；表示鄰域依賴度；λ和μ分別表示分類質量和子集長度的重要程度，兩個參數和的設置參照文獻［3］。

2.3 算法描述

依據鄰域粗糙集模型和MBO算法原理，用BMBOM算法選出特征子集，通過適應度函數評估特征子集的適應度值，排序選出最優特征子集，則特征選擇算法的偽代碼如算法2所示。

算法2 基于鄰域粗糙集與BMBOM的特征選擇算法（FSNB）。

輸出 最優特征子集。

1） While 不滿足最大迭代或停止條件 do

2） 根據式（13）計算適應度值并排序，找到最優的帝王蝶位置和其對應的適應度值；

11） else

14） end if

15） end for

16） end for

21） else

27） end if

28） end if

29） end for

30） end for

31） 將新生成的子種群合并為1個整體種群；

33） End while

35）計算所有特征在測試集上的分類精度；

36）輸出最佳解決方案的位置（選中的最優特征子集）。

下面給出算法2的時間復雜度分析：假設帝王蝶群體規模為N、子群1為N1、子群2為1、最大迭代次數為T、空間維度為D。由文獻［22］可知，計算正域和鄰域依賴度的時間復雜度為。FSNB的復雜度由每次迭代循環確定，具體分析如下：步驟2）使用鄰域依賴度計算適應度函數，其時間復雜度為；步驟3）～4）的時間復雜度都為O（N）；步驟5）～16）的時間復雜度為O（N1D）；步驟17）～30）的時間復雜度為；步驟31）～33）的時間復雜度為O（N）；步驟34）～36）的時間復雜度為常數項。因此，FSNB在最壞情況下的總時間復雜度為O（TN2）。

3 實驗與結果分析

3.1 BMBOM算法性能分析

為驗證BMBOM算法的優化性能，選取文獻［20］中典型的6個基準函數（如表1所示），與MBO算法［17］、粒子群優化（Particle Swarm Optimization， PSO）算法［8］進行測試與比較。表1中，單峰函數主要測試算法的尋優精度；多峰函數具有多個局部最優點檢驗算法的全局搜索性能和避免局部收斂的能力。這些函數的理論最優值為0。為了確保實驗的公平性，依據文獻［20］，這3種算法在30維上設置相同的參數。同時，為防止產生隨機的實驗結果影響對算法的評估，這3種算法在6個基準函數上獨立運行30次。表2給出了3種算法在6個基準函數上30維的最優值、最差值、平均值、標準差和運行時間的測試結果。從表2測試結果可以看出，在上，BMBOM算法的最優值、最差值、平均值以及標準差都優于MBO算法和PSO算法；尤其在f1和f5上，BMBOM算法的5項指標遠領先于其他2種算法；在f6上，PSO算法在標準差上是最優的，BMBOM算法在f6的最優值、最差值和平均值都是最優的。從運行時間上來說，BMBOM算法次于其他2種對比算法，其原因是：BMBOM算法中的局部擾動、群體劃分策略以及突變算子在提高了優化性能的同時增加了運行時間。因此，這3種算法在6個基準函數30維上的實驗結果表明，BMBOM算法獲得的優化能力和穩定性是相對優異的。實驗環境設置為64位Window 7、Intel Core i5 2.2 GHz CPU、4 GB RAM和Matlab 2016b，且文中所有實驗結果中的加粗都表示最佳值。

表1 六個基準函數信息Tab. 1 Information of six benchmark functions

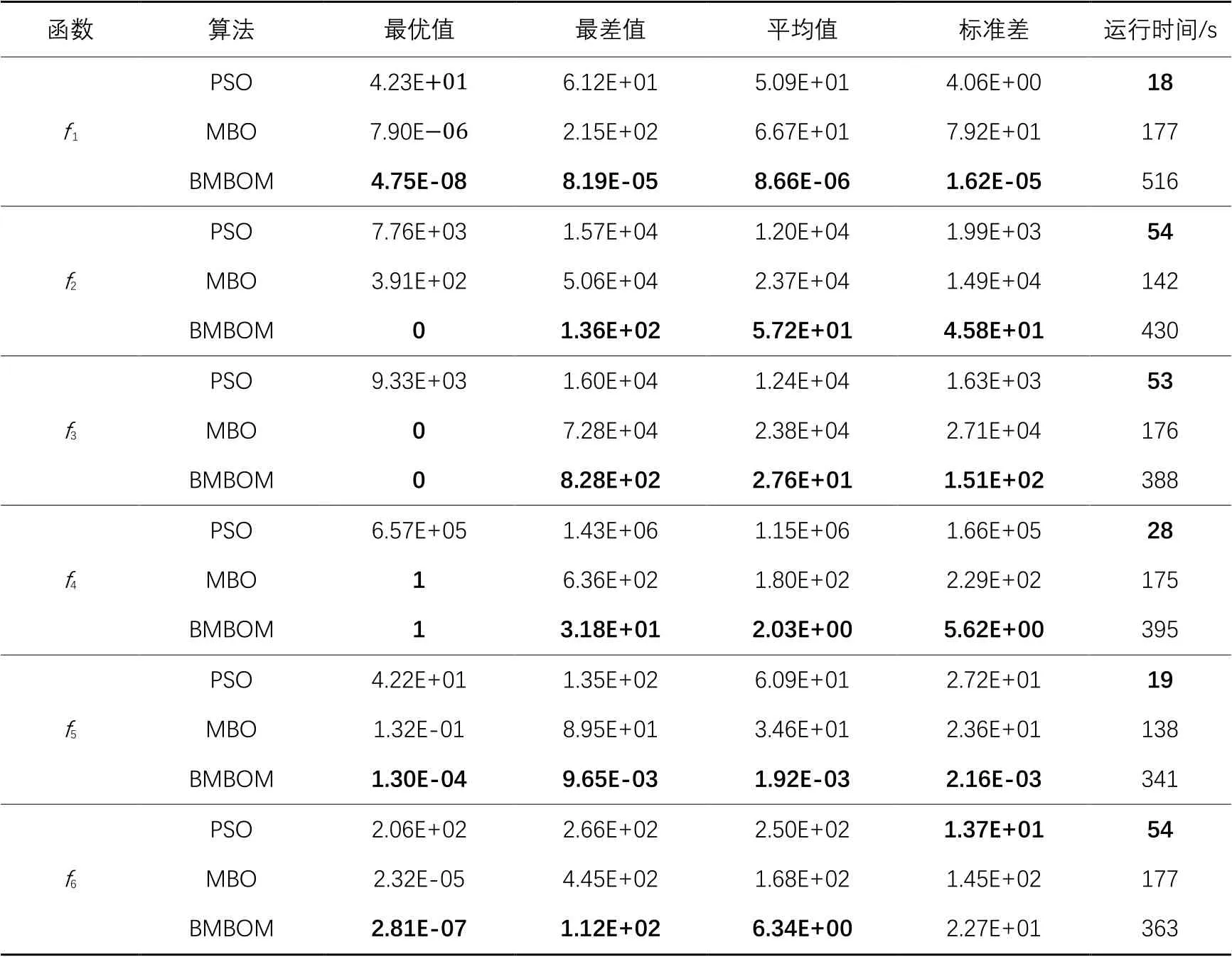
表2 三種優化算法在6個基準函數30維上的實驗結果Tab. 2 Experimental results of three optimization algorithms on 30-dimensions of six benchmark functions

3.2 FSNB性能分析

為驗證FSNB的特征選擇效果，選用14個UCI數據集［21］進行測試。表3給出了所選數據集的信息。FSNB的種群數設置為20，最大迭代次數設置為100，依據文獻［3］，設置適應度函數中且。實驗采用3類評價指標［21］：分類精度、所選特征數和適應度值。為了驗證結果的最優性并確保比較算法的公平性，參照文獻［21］使用K最近鄰分類器（），將每個數據集分為訓練集占80%和測試集占20%。為了避免算法的隨機性，每種算法獨立運行20次，因而統計測量是20次獨立運行的總體能力和最終結果。

3.2.1 與基于粗糙集的優化特征選擇算法的比較

為了驗證算法的有效性，首先將所提的FSNB與5種基于粗糙集的優化特征選擇算法進行比較，分別包括：ARRSFA（Attribute Reduction based on Rough Sets and the discrete Firefly Algorithm）［23］、PSORSFS（Feature Selection algorithm based on Rough Sets and Particle Swarm Optimization）［24］、FSARSR（Rough Set Reducts with Fish Swarm Algorithm）［25］、QCSIA_FS（Cooperative Swarm Intelligence Algorithm based on Quantum-inspired and rough sets for Feature Selection）［26］、DQBGOA_MR（Dynamic population Quantum Binary Grasshopper Optimization Algorithm based on Mutual information and Rough set）［10］。這些算法使用對應文獻中的最佳實驗參數，對比的實驗數據與結果選自文獻［10］。表4給出了FSNB與其他5種特征選擇算法在10個UCI數據集上的分類精度的實驗結果。從表4可以看出，在Vote數據集上，FSNB比最優的FSARSR略差1.3個百分點；在其他9個數據集上，FSNB的分類精度都是最優的，尤其是在Wine數據集上，FSNB的分類精度比其他5種算法遠高出23.3～29.9個百分點。同時，FSNB在分類精度平均值上是最優的，提升了11.6～14.0個百分點。由此可以說明，FSNB能夠獲得最優的分類精度。

表5給出了FSNB與其他5種特征選擇算法所選擇的特征數的實驗結果。在Spect、Tic-tac-toe和Vote這3個數據集上，FSNB比其他5種算法具有顯著優勢。在Lungcancer數據集上，FSNB獲取的特征數略遜于DQBGOA_MR，但是結合表4的分類精度綜合分析可知，FSNB的分類性能遠優于DQBGOA_MR。同樣的，在其余6個數據集上，盡管FSNB所選的特征數不如其他5種算法，但是它們之間的差值較小，同時FSNB獲得了具有明顯優勢的分類精度。綜合考慮表4～5的實驗結果可知，FSNB的分類能力優于其他5種算法。

表3 14個UCI數據集信息Tab. 3 Information of fourteen UCI datasets

表4 FSNB與5種基于粗糙集的優化特征選擇算法的分類精度實驗結果 單位： %Tab. 4 Experimental results of FSNB and five optimized feature selection algorithms based on rough sets on classification accuracy unit： %

表5 FSNB與5種基于粗糙集的優化特征選擇算法的所選特征數實驗結果Tab. 5 Experimental results of FSNB and five optimized feature selection algorithms based on rough set on number of selected features

接下來，為了進一步評估FSNB的分類性能，選用當前流行的8種優化算法：IRRA（Improved Runner-Root Algorithm）［27］、GA（Genetic Algorithm）［28］、PSO（Particle Swarm Optimization）［29］、ABC（Artificial Bee Colony）［30］、FA（Firefly Algorithm）［31］、SSO（Social Spider Optimization）［32］、CS（Cuckoo Search）［33］和HS（Harmony Search algorithm）［34］，與粗糙集 （Rough Set）模型結合，構造8種特征選擇算法進行對比，分別簡寫為IRRARS、GARS、PSORS、ABCRS、FARS、SSORS、CSRS和HSRS。上述8種優化算法使用對應文獻中的最佳實驗參數，對比的實驗數據與結果選自文獻［27］。表6給出了FSNB與上述8種特征選擇算法在7個UCI數據集上的分類精度的實驗結果。從表6的比較結果可知，在Breastcancer數據集上，FSNB的分類精度比IRRARS略低了2.3個百分點，但是優于GARS、PSORS、FARS、SSORS和CSRS這5種算法；在Lungcancer數據集上，FSNB的分類精度比其他8種算法高出了13.2～29.2個百分點；在Heart、Ionosphere、Waveform和Zoo這4個數據集上，FSNB也明顯優于其他8種算法，同時也獲得了相對最好的分類精度；而在Congress數據集上，FSNB的分類精度并沒有其他8種算法好，但是在選擇的特征數上來講，FSNB占據了絕對的優勢。盡管FSNB在Breastcancer和Congress數據集上的分類精度不是最優的，但相較于其余8種算法，FSNB還是具有較好的優勢。同時，FSNB在分類精度平均值上是最高的，提升了3.9～13.2個百分點。表7中給出了FSNB和其他8種算法所選特征數。與這8種結合粗糙集的元啟發式特征選擇算法相比，FSNB在7個數據集上表現出了優越的性能，所選特征數遠少于其他8種算法。詳細來說，在Waveform數據集上，GARS所選特征數是FSNB的606倍；在Breastcancer和Congress這2個數據集上，FSNB雖然沒有獲得最高分類精度，但是選擇的特征數取得了最小值，尤其是IRRARS和SSORS這2個算法選擇的特征數分別是FSNB的57倍和30倍，表明FSNB的分類性能是最優的。

總的來說，從表4～7的實驗結果可以看出，與粗糙集和優化算法結合的特征選擇算法相比，FSNB在選擇較少的特征的同時能夠保持良好的分類精度。這表明FSNB選出的特征子集具有較少的數量和較高的分類精度，驗證了FSNB的有效性。

表6 FSNB與8種結合粗糙集與優化算法的特征選擇算法的分類精度實驗結果 單位： %Tab. 6 Experimental results of FSNB and eight feature selection algorithms combining rough set and optimization algorithm on classification accuracy unit： %

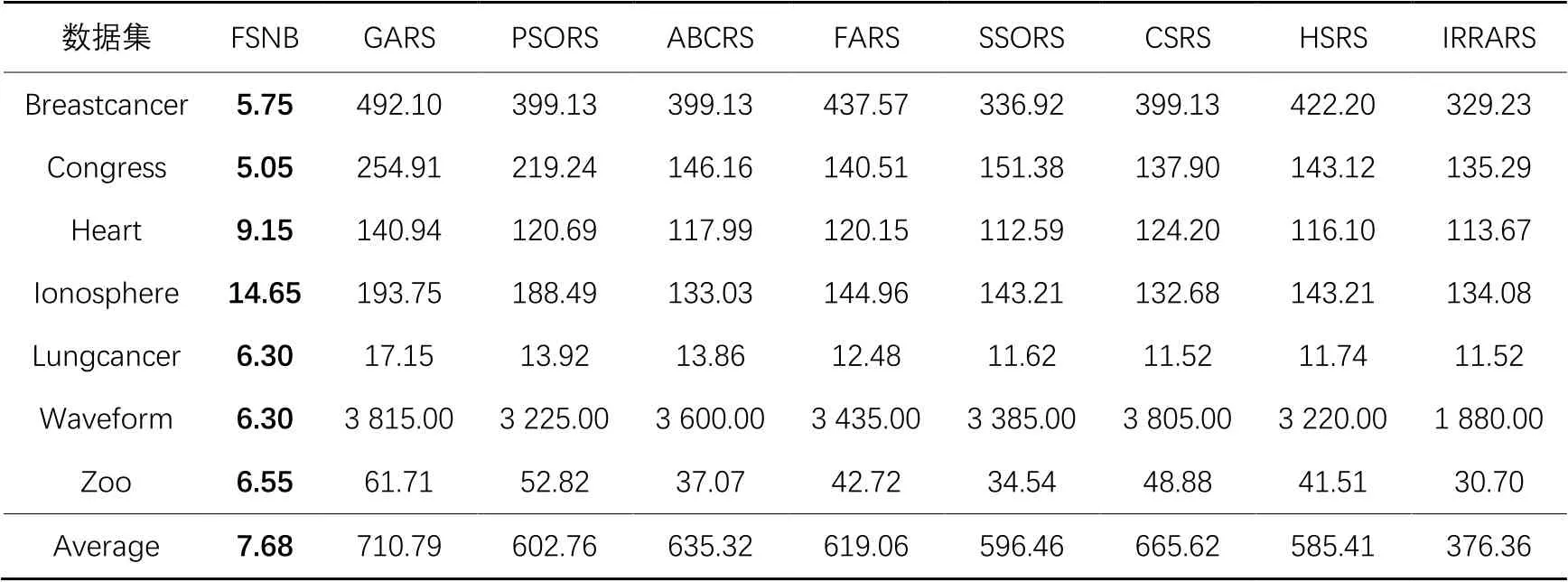
表7 FSNB與8種結合粗糙集與優化算法的特征選擇算法所選特征數實驗結果Tab. 7 Experimental results of FSNB and eight feature selection algorithms combining rough set and optimization algorithm on number of selected features

3.2.2 與基于鄰域粗糙集的優化特征選擇算法的比較

首先將鄰域粗糙集與文獻［17］的MBO算法相結合，構建新的特征選擇算法FSNM（Feature Selection algorithm based on NRS and MBO），在選定的14個UCI數據集上，比較FSNM和FSNB的性能，驗證BMBOM算法的優化性能。表8給出了3類指標的實驗結果。

從表8可以看出，在14個UCI數據集上，FSNB獲得了最優的分類精度和最少的特征數。詳細來說，在Wine數據集上為最高分類精度97.53%；在Zoo、Waveform和Breastcancer這3個數據集上次之，分別為97.14%、96.89%和95.67%。在Congress和Heart這2個數據集上，FSNB的適應度值略低于FSNM，但是在分類精度和特征數上都優于FSNM。此外，在Waveform數據集上，FSNB選擇的特征數最少，即為6.30。

同時，從表8可以看出，在Breastercancer、Hepatitis、Ionosphere等12個數據集上，FSNB獲得了最優的適應度值，同時，在適應度值上，FSNB的平均值也是最優的。從運行時間上看出，在Breastcancer、Hepatitis、Ionosphere、Lungcancer、Lymphography、Waveform和Zoo這7個數據集上，FSNB優于FSNM，尤其是在Lymphography數據集上，FSNB的運行時間不到FSNM的6%；在Congress、Heart、Sonar和Wine這4個數據集上，FSNB與FSNM的運行時間是一樣的；在Spect、Tic-tac-toe和Vote這3個數據集上，FSNB的運行時間次于FSNM；在平均值上，FSNB仍然優于FSNM。

從表8的4個評價指標總體結果來說，FSNB的分類結果優于FSNM。也就是說，BMBOM算法具有較好的優化分類性能。

接下來，為了驗證FSNB的分類性能，選用當前流行的8種優化算法：IRRA［27］、GA［28］、PSO［29］、ABC［30］、FA［31］、SSO［32］、CS［33］和HS［34］，與鄰域粗糙集模型結合構造8種特征選擇算法進行對比，分別簡寫為IRRANRS、GANRS、PSONRS、ABCNRS、FANRS、SSONRS、CSNRS和HSNRS。對比的實驗數據選自文獻［27］。表9給出了FSNB與其他8種算法在分類精度上的實驗比較結果。表10描述了FSNB與其他8種算法所選特征數的對比結果。

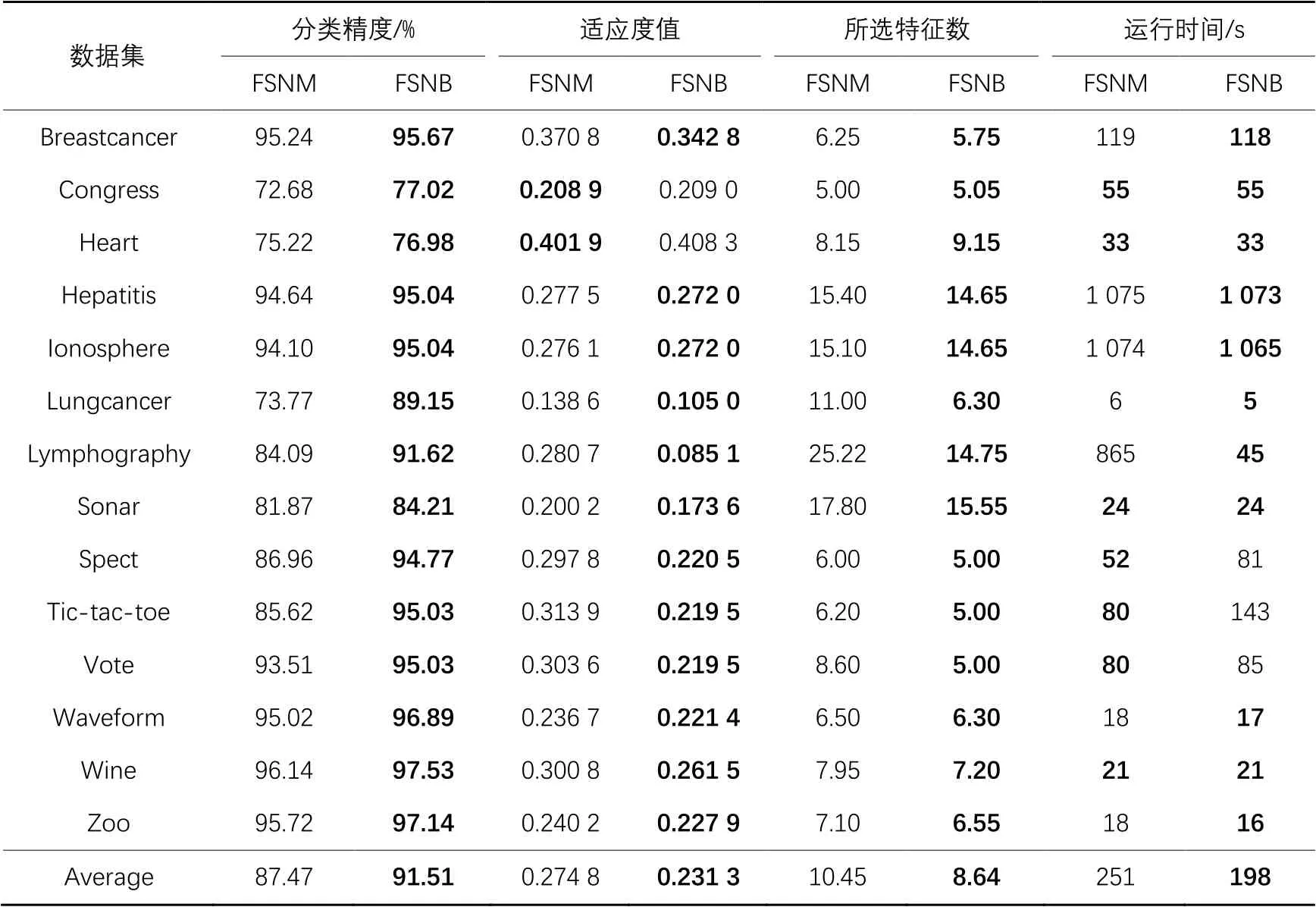
表8 FSNB與FSNM在分類精度、適應度值和所選特征數上的實驗結果Tab. 8 Experimental results of FSNM and FSNB on classification accuracy， fitness value and number of selected features

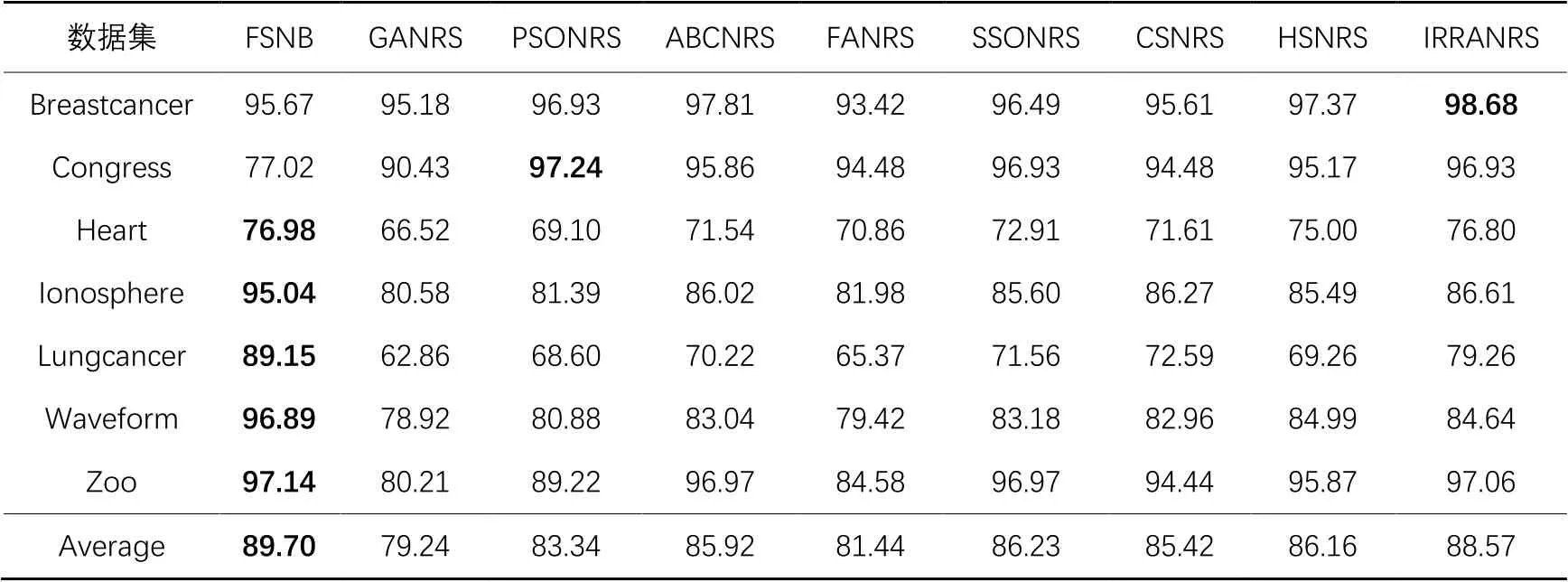
表9 FSNB與8種結合鄰域粗糙集與優化算法的特征選擇算法的分類精度實驗結果 單位： %Tab. 9 Experimental results of FSNB and eight feature selection algorithms combining NRS and optimization algorithms on classification accuracy unit： %

表10 FSNB與8種結合鄰域粗糙集與優化算法的特征選擇算法所選特征數實驗結果Tab. 10 Experimental results of FSNB and eight feature selection algorithms combining NRS and optimization algorithms on number of selected features

從表9可以看出，對于Heart、Ionosphere、Lungcancer、Waveform和Zoo這5個數據集，FSNB的性能最優。FSNB在除了Congress以外的6個數據集上都優于GANRS、FANRS和CSNRS這3個算法。值得一提的是，在Lungcancer數據集上，FSNB的分類精度明顯優于其他8種算法。此外，在Zoo數據集上，FSNB的分類精度高達97.14%；而在Congress數據集上，FSNB的分類精度略低于其他8種算法，這可能是FSNB在迭代的過程中丟失了一些重要的特征，導致分類精度降低。

根據表10可知，在7個數據集上，FSNB選擇的特征數依舊是最少的。尤其在Waveform數據集上，GANRS的特征數是FSNB的588倍。在Breastcancer和Congress這2個數據集上，FSNB雖然沒有獲得最高的分類精度，但是選擇的特征數是最少的，并且IRRANRS和PSONRS這2個算法選擇的特征數分別是FSNB的54倍和41倍。

總的來說，在Heart、Ionosphere、Lungcancer、Waveform和Zoo這5個數據集上，FSNB的分類精度是穩定的，而GANRS、ABCNRS、FANRS、CSNRS和HSNRS這5種算法的分類性能是不穩定的。同時，FSNB在分類精度和特征數上總的平均值都是最優的，即在分類精度平均值上提升了1.1～10.5個百分點，在所選特征數的平均值上比其他算法少了347～678。因此，FSNB能夠有效消除冗余特征并顯著提高算法的分類精度，優于其他8種算法，也就是說FSNB在解決特征選擇問題上具有明顯的優勢。

3.2.3 與基于二進制灰狼優化的特征選擇算法的比較

為了更好地展示FSNB的有效性，從文獻［3］中選擇6種基于二進制灰狼優化（Binary Grey Wolf Optimizer）的特征選擇算法，具體包括：BGWO、ABGWO、ABGWO-V1、ABGWO-V2、ABGWO-V3和ABGWO-V4，與本文提出的FSNB進行實驗比較。上述6種算法使用文獻［3］中對應的最佳實驗參數，對比的實驗數據與結果也選自文獻［3］。表11給出了FSNB與6種基于二進制灰狼優化的特征選擇算法的分類精度比較結果。

從表11可以看出，在Congress數據集上，FSNB的分類精度略低于最優的ABGWO。但是，在其余8個數據集上，FSNB獲得最優的分類精度，尤其是在Zoo數據集上的分類精度最高，即為97.14%；在Lymphography數據集上，FSNB的分類精度明顯比其他6種算法高出44.1～45.4個百分點。同時，FSNB在分類精度的平均值上是最優的，即提升了13.5～14.3個百分點。

表12給出了FSNB與其他6種算法所選特征數比較結果。從表12可以看出，FSNB表現最優，其次是ABGWO-V2和ABGWO-V3這2種算法。在Congress、Sonar、Spect、Tic-tac-toe、Waveform和Zoo這6個數據集上，FSNB選取的特征數為最小值。在Breastcancer和Ionosphere這2個數據集上，雖然FSNB的特征數都不如ABGWO-V2算法，但FSNB的分類精度值分別比ABGWO-V2算法高出15.4個百分點和8.1個百分點；而在Lymphography數據集上，FSNB的特征數少于ABGWO-V3算法，但FSNB的分類精度是7種算法中最高的。總體來說，綜合考慮分類精度和所選特征數這2個評價指標，FSNB明顯優于這6種基于二進制灰狼優化的特征選擇算法。

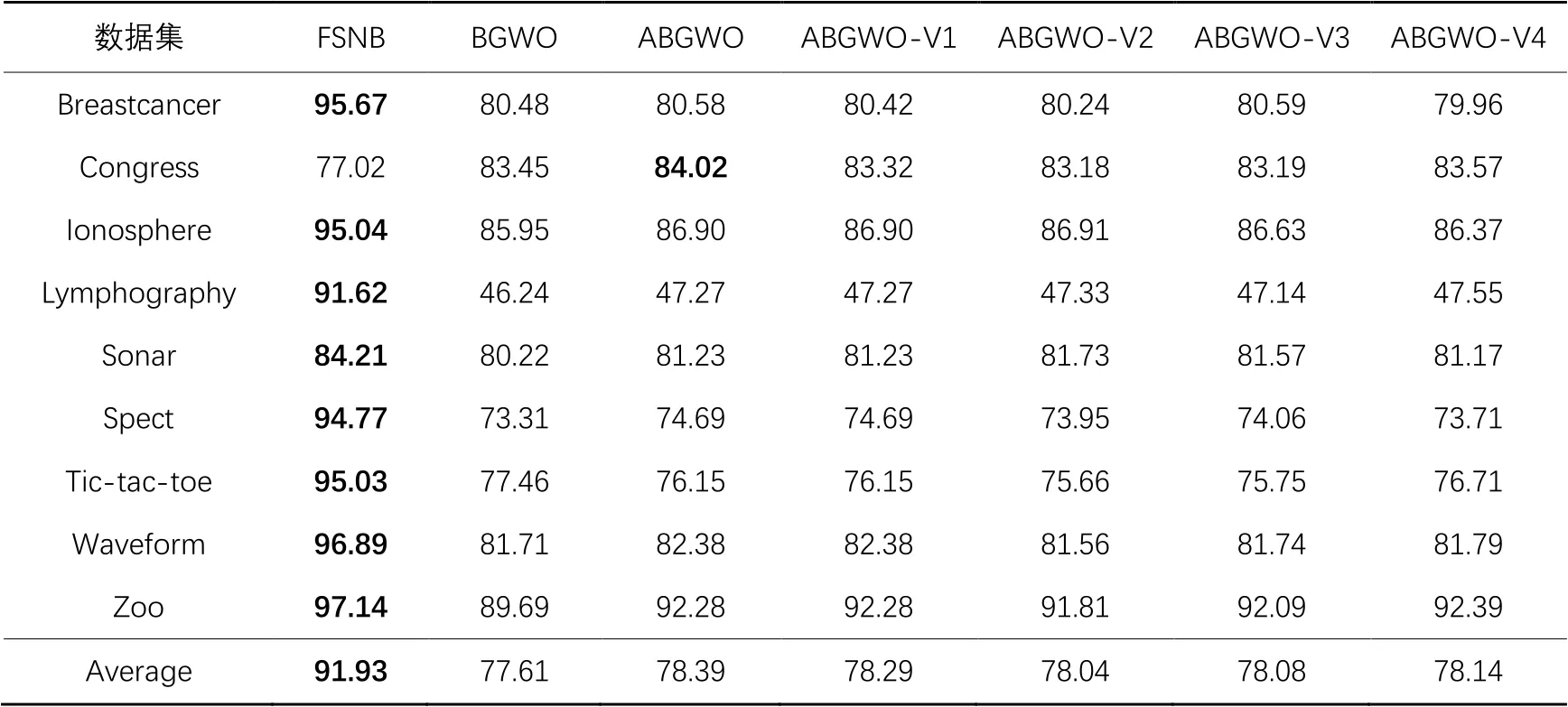
表11 FSNB與6種基于二進制灰狼優化的特征選擇算法的分類精度實驗結果 單位： %Tab. 11 Experimental results of FSNB and six feature selection algorithms based on binary grey wolf optimizer on classification accuracy unit： %

表12 FSNB與6種基于二進制灰狼優化的特征選擇算法所選特征數實驗結果Tab. 12 Experimental results of FSNB and six feature selection algorithms based on binary grey wolf optimizer on number of selected features

3.3 統計分析

使用Friedman和Bonferroni-Dunn測試［35］來分析所有實驗結果的統計意義，計算式為：

其中：k是算法數量；N是數據集數量；Ri是k個算法在N個數據集上的平均排名。依據測試結果可知，如果平均距離水平超出臨界距離，則算法性能有顯著差異。臨界距離定義為：

其中：qα是測試的關鍵列表值；α表示顯著水平。

依據表5、7、9、11的分類精度實驗結果，分別對所有比較的算法進行Friedman檢驗，驗證所有算法在分類性能上是否存在顯著性差異，表13～16分別給出了在KNN分類器下的排序結果和2個評價指標（和）的值。

為了直觀地顯示FSNB與其他對比算法的相對性能，圖1給出了比較的算法在分類精度下的值，其中每個算法的平均排序沿數軸繪制。軸上的最小值位于左側，因此，左側排序的算法更好。表13給出了FSNB與5種基于粗糙集的優化特征選擇算法的平均排序和值，其中，的零假設被拒絕。如圖1所示，在顯著性水平下，，，其中且，由此可知，FSNB明顯優于其他5種算法。表14給出了FSNB與8種結合粗糙集與優化的特征選擇算法的平均排序和值，其中的臨界值為，時拒絕零假設。圖2顯示了在顯著性水平下，，，其中且，由此可以看出，IRRARS結果最優，FSNB次之，但是FSNB優于其他7種算法。表15給出了FSNB與8種結合鄰域粗糙集與優化的特征選擇算法的平均排序和值，其中的臨界值為1.802，時的零假設將被拒絕。如圖3所示，在顯著性水平下，，其中且。因而可知，IRRANRS最優，FSNB次之，但是FSNB優于其他7種算法。表16給出了FSNB與6種基于二進制灰狼優化的特征選擇算法的平均排序以及值，其中的臨界值為1.901，時的零假設被拒絕。圖4顯示了在時，，其中且。因此，FSNB的Bonferron-Dunn檢驗優于其他6種算法。

總的來說，通過上述統計結果的分析可知，FSNB的性能優于其他比較算法，并在所有數據集上實現了良好的泛化性能。

表13 FSNB與5種基于粗糙集的優化特征選擇算法的統計檢驗Tab. 13 Statistical test of FSNB and five optimized feature selection algorithms based on rough set

表14 FSNB與8種結合粗糙集與優化算法的特征選擇算法的統計檢驗Tab. 14 Statistical test of FSNB and eight feature selection algorithms combining rough set and optimization algorithms

表15 FSNB與8種結合鄰域粗糙集與優化算法的特征選擇算法的統計檢驗Tab. 15 Statistical test of FSNB and eight feature selection algorithms combining NRS and optimization algorithms

表16 FSNB與6種基于二進制灰狼優化的特征選擇算法的統計檢驗Tab. 16 Statistical test of FSNB and six feature selection algorithms based on binary grey wolf optimizer

圖1 FSNB與5種基于粗糙集的優化特征選擇算法的Bonferroni-Dunn檢驗結果Fig. 1 Bonferroni-Dunn test results of FSNB and five optimized feature selection algorithms based on rough set

圖2 FSNB與8種結合粗糙集與優化算法的特征選擇算法的Bonferroni-Dunn檢驗結果Fig. 2 Bonferroni-Dunn test results of FSNB and eight feature selection algorithms based on rough set and optimization algorithms

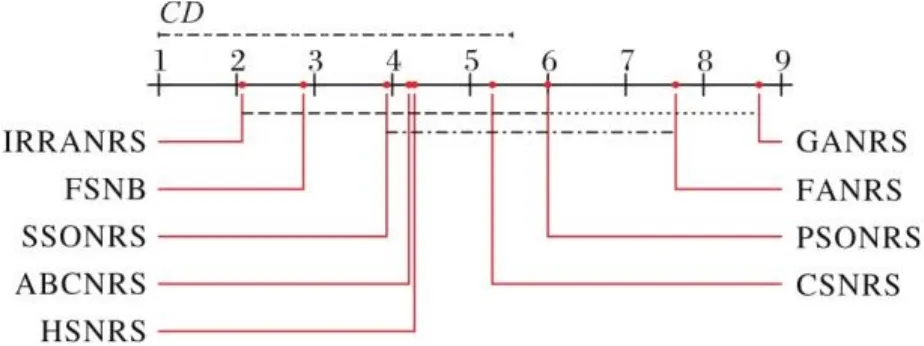
圖3 FSNB與8種結合鄰域粗糙集與優化算法的特征選擇算法的Bonferroni-Dunn檢驗結果Fig. 3 Bonferroni-Dunn test results of FSNB and eight feature selection algorithms based on NRS and optimization algorithms

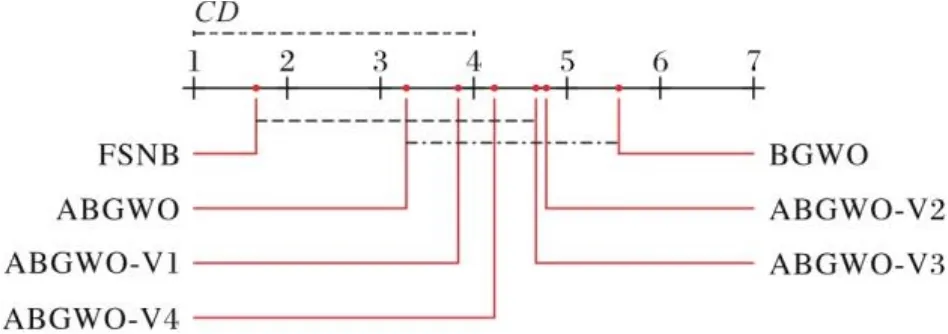
圖4 FSNB與6種基于二進制灰狼優化的特征選擇算法的Bonferroni-Dunn檢驗結果Fig. 4 Bonferroni-Dunn test results of FSNB and six feature selection algorithms based on binary grey wolf optimizer

4 結語

本文利用MBO算法的計算簡單、所需計算參數較少、收斂迅速等優點，提出了一種基于鄰域粗糙集與改進的MBO的特征選擇算法。首先，針對獲取的數據構建鄰域決策系統，設計了BMBOM算法；然后，基于鄰域粗糙集構造適應度函數，評估初始化的特征子集的適應度值并排序；最后，使用BMBOM算法搜索最優特征子集，設計了一種元啟發式的特征選擇算法。在6個基準函數和14個UCI數據集上的實驗結果表明，所提算法是有效的。究其原因是在MBO算法上加入了局部擾動和群體劃分策略，促使MBO算法能夠最大化地搜索特征空間達到最優，加入突變算子使改進的MBO算法的多樣性增強，進而更容易收斂到最優/接近最優解。將鄰域粗糙集模型與改進的MBO算法相結合，使該特征選擇算法更快地找到最小特征子集，特別是在處理高維數據時效果更加明顯。但是，在算法運行時效上，本文所提算法的改善效果不夠顯著，在下一步研究工作中需繼續改進。

[1] 吳信東，董丙冰，堵新政，等.數據治理技術［J］.軟件學報，2019，30（9）：2830-2856.（WU X D， DONG B B， DU X Z， et al. Data governance technology ［J］. Journal of Software， 2019， 30（9）： 2830-2856.）

[2] 鄧威，郭釔秀，李勇，等.基于特征選擇和Stacking集成學習的配電網網損預測［J］.電力系統保護與控制，2020，48（15）：108-115.（DENG W， GUO Y X， LI Y， et al. Power losses prediction based on feature selection and Stacking integrated learning ［J］. Power System Protection and Control， 2020， 48（15）： 108-115.）

[3] HU P， PAN J S， CHU S C. Improved binary grey wolf optimizer and its application for feature selection ［J］. Knowledge-Based Systems， 2020，195： Article No.105746.

[4] TUBISHAT M， IDRIS N， SHUIB L， et al. Improved salp swarm algorithm based on opposition based learning and novel local search algorithm for feature selection ［J］. Expert Systems with Applications， 2020， 145： Article No.113122.

[5] 劉艷，程璐，孫林.基于K-S檢驗和鄰域粗糙集的特征選擇方法［J］.河南師范大學學報（自然科學版），2019，47（2）：21-28.（LIU Y， CHENG L， SUN L. Feature selection method based on K-S test and neighborhood rough sets ［J］. Journal of Henan Normal University （Natural Science Edition）， 2019， 47（2）： 21-28.）

[6] 劉琨，封碩.加強局部搜索能力的人工蜂群算法［J］.河南師范大學學報（自然科學版），2021，49（2）：15-24.（LIU K， FENG S. An improved artificial bee colony algorithm for enhancing local search ability ［J］. Journal of Henan Normal University （Natural Science Edition）， 2021， 49（2）： 15-24.）

[7] ZAIMOGLU E A， CELEBI N， YURTAY N. Binary-coded tug of war optimization algorithm for attribute reduction based on rough set ［J］. Journal of Multiple-Valued Logic and Soft Computing， 2020， 35（1/2）： 93-111.

[8] HUDA R K， BANKA H. Efficient feature selection and classification algorithm based on PSO and rough sets ［J］. Neural Computing and Applications， 2019， 31（8）： 4287-4303.

[9] TAWHID M A， IBRAHIM A M. Feature selection based on rough set approach， wrapper approach， and binary whale optimization algorithm ［J］. International Journal of Machine Learning and Cybernetics， 2020， 11（3）： 573-602.

[10] WANG D， CHEN H M， LI T R， et al. A novel quantum grasshopper optimization algorithm for feature selection ［J］. International Journal of Approximate Reasoning， 2020， 127： 33-53.

[11] ABD EL AZIZ M， HASSANIEN A E. Modified cuckoo search algorithm with rough sets for feature selection ［J］. Neural Computing and Applications， 2018， 29（4）： 925-934.

[12] ZOU L， LI H X， JIANG W， et al. An improved fish swarm algorithm for neighborhood rough set reduction and its application ［J］. IEEE Access，2019， 7： 90277-90288.

[13] 薛占熬，龐文莉，姚守倩，等.基于前景理論的直覺模糊三支決策模型［J］.河南師范大學學報（自然科學版），2020，48（5）：31-36，79.（XUE Z A， PANG W L， YAO S Q， et al. The prospect theory based intuitionistic fuzzy three-way decisions model ［J］. Journal of Henan Normal University （Natural Science Edition）， 2020， 48（5）： 31-36， 79.）

[14] HU Q H， YU D R， LIU J F， et al. Neighborhood rough set based heterogeneous feature subset selection ［J］. Information Sciences， 2018， 178（18）： 3577-3594.

[15] 彭鵬，倪志偉，朱旭輝，等.基于改進二元螢火蟲群優化算法和鄰域粗糙集的屬性約簡方法［J］.模式識別與人工智能，2020，33（2）：95-105.（PENG P， NI Z W， ZHU X H， et al. Attribute reduction method based on improved binary glowworm swarm optimization algorithm and neighborhood rough set ［J］. Pattern Recognition and Artificial Intelligence， 2020， 33（2）： 95-105.）

[16] SUN L， CHEN S S， XU J C， et al. Improved monarch butterfly optimization algorithm based on opposition-based learning and random local perturbation ［J］. Complexity， 2019， 2019： Article No.4182148.

[17] WANG G G， DEB S， CUI Z H. Monarch butterfly optimization ［J］. Neural Computing and Applications， 2019， 31（7）： 1995-2014.

[18] DORGHAM O M， ALWESHAH M， RYALAT M H， et al. Monarch butterfly optimization algorithm for computed tomography image segmentation ［J］. Multimedia Tools and Applications， 2021， 80（20）： 30057-30090.

[19] SOLTANI P， HADAVANDI E. A monarch butterfly optimization- based neural network simulator for prediction of siro-spun yarn tenacity ［J］. Soft Computing， 2019， 23（20）： 10521-10535.

[20] 孫林，趙婧，徐久成，等.基于改進帝王蝶優化算法的特征選擇方法［J］.模式識別與人工智能，2020，33（11）：981-994.（SUN L， ZHAO J， XU J C， et al. Feature selection method based on improved monarch butterfly optimization algorithm ［J］. Pattern Recognition and Artificial Intelligence， 2020， 33（11）： 981-994.）

[21] MAFARJA M， ALJARAH I， FARIS H， et al. Binary grasshopper optimisation algorithm approaches for feature selection problems ［J］. Expert Systems with Applications， 2019， 117： 267-286.

[22] SUN L， WANG L Y， DING W P， et al. Feature selection using fuzzy neighborhood entropy-based uncertainty measures for fuzzy neighborhood multigranulation rough sets ［J］. IEEE Transactions on Fuzzy Systems， 2021， 29（1）： 19-33.

[23] LONG N C， MEESAD P， UNGER H. Attribute reduction based on rough sets and the discrete firefly algorithm ［M］// BOONKRONG S， UNGER H， MEESAD P. Recent Advances in Information and Communication Technology，AISC 265. Cham： Springer， 2014： 13-22.

[24] WANG X Y， YANG J， TENG X L， et al. Feature selection based on rough sets and particle swarm optimization ［J］. Pattern Recognition Letters， 2007， 28（4）： 459-471.

[25] CHEN Y M， ZHU Q X， XU H R. Finding rough set reducts with fish swarm algorithm ［J］. Knowledge-Based Systems， 2015， 81： 22-29.

[26] ZOUACHE D， BEN ABDELAZIZ F. A cooperative swarm intelligence algorithm based on quantum-inspired and rough sets for feature selection ［J］. Computers and Industrial Engineering， 2018， 115： 26-36.

[27] IBRAHIM R A， ABD ELAZIZ M， OLIVA D， et al. An improved runner-root algorithm for solving feature selection problems based on rough sets and neighborhood rough sets ［J］. Applied Soft Computing， 2020，97（Pt B）： Article No.105517.

[28] JING S Y. A hybrid genetic algorithm for feature subset selection in rough set theory ［J］. Soft Computing， 2014， 18（7）： 1373-1382.

[29] ZHANG Y， GONG D W， HU Y， et al. Feature selection algorithm based on bare bones particle swarm optimization ［J］. Neurocomputing， 2015， 148： 150-157.

[30] SUGUNA N， THANUSHKODI K G. An independent rough set approach hybrid with artificial bee colony algorithm for dimensionality reduction ［J］. American Journal of Applied Sciences， 2011， 8（3）： 261- 266.

[31] 汪春峰，褚新月.基于精英鄰居引導的螢火蟲算法［J］.河南師范大學學報（自然科學版），2019，47（6）：15-21.（WAND C F， CHU X Y. A firefly algorithm based on elite neighborhood guide ［J］. Journal of Henan Normal University （Natural Science Edition）， 2019， 47（6）： 15-21.）

[32] ABD EL AZIZ M， HASSANIEN A E. An improved social spider optimization algorithm based on rough sets for solving minimum number attribute reduction problem ［J］. Neural Computing and Applications， 2018， 30（8）： 2441-2452.

[33] 徐小琴，王博，趙紅生，等.基于布谷鳥搜索和模擬退火算法的兩電壓等級配網重構方法［J］.電力系統保護與控制，2020，48（11）：84-91.（XU X Q， WANG B， ZHAO H S， et al. Reconfiguration of two-voltage distribution network based on cuckoo search and simulated annealing algorithm ［J］. Power System Protection and Control， 2020， 48（15）： 108-115.）

[34] INBARANI H H， BAGYAMATHI M， AZAR A T. A novel hybrid feature selection method based on rough set and improved harmony search ［J］. Neural Computing and Applications， 2015， 26（8）： 1859-1880.

[35] SUN L， WANG L Y， DING W P， et al. Neighborhood multi- granulation rough sets-based attribute reduction using Lebesgue and entropy measures in incomplete neighborhood decision systems ［J］. Knowledge-Based Systems， 2020， 192： Article No.105373.

Feature selection algorithm based on neighborhood rough set and monarch butterfly optimization

SUN Lin1，2*， ZHAO Jing1， XU Jiucheng1，2， WANG Xinya1

（1.College of Computer and Information Engineering，Henan Normal University，Xinxiang Henan453007，China；2.Key Laboratory of Artificial Intelligence and Personalized Learning in Education of Henan Province（Henan Normal University），Xinxiang Henan453007，China）

The classical Monarch Butterfly Optimization （MBO） algorithm cannot handle continuous data well， and the rough set model cannot sufficiently process large-scale，high-dimensional and complex data. To address these problems， a new feature selection algorithm based on Neighborhood Rough Set （NRS） and MBO was proposed. Firstly， local disturbance， group division strategy and MBO algorithm were combined， and a transmission mechanism was constructed to form a Binary MBO （BMBO） algorithm. Secondly， the mutation operator was introduced to enhance the exploration ability of this algorithm， and a BMBO based on Mutation operator （BMBOM） algorithm was proposed. Then， a fitness function was developed based on the neighborhood dependence degree in NRS， and the fitness values of the initialized feature subsets were evaluated and sorted. Finally， the BMBOM algorithm was used to search the optimal feature subset through continuous iterations， and a meta-heuristic feature selection algorithm was designed. The optimization performance of the BMBOM algorithm was evaluated on benchmark functions， and the classification performance of the proposed feature selection algorithm was evaluated on UCI datasets. Experimental results show that， the proposed BMBOM algorithm is significantly better than MBO and Particle Swarm Optimization （PSO） algorithms in terms of the optimal value， worst value， average value and standard deviation on five benchmark functions. Compared with the optimized feature selection algorithms based on rough set， the feature selection algorithms combining rough set and optimization algorithms， the feature selection algorithms combining NRS and optimization algorithms，the feature selection algorithms based on binary grey wolf optimization， the proposed feature selection algorithm performs well in the three indicators of classification accuracy， the number of selected features and fitness value on UCI datasets，and can select the optimal feature subset with few features and high classification accuracy.

Monarch Butterfly Optimization (MBO); feature selection; Neighborhood Rough Set (NRS); neighborhood dependence degree; binary

TP181

A

1001-9081（2022）05-1355-12

10.11772/j.issn.1001-9081.2021030497

2021?04?02；

2021?09?15；

2021?09?22。

國家自然科學基金資助項目（62076089，61772176，61976082）；河南省科技攻關項目（212102210136）。

孫林（1979—），男，河南南陽人，副教授，博士，CCF會員，主要研究方向：粒計算、數據挖掘、機器學習、生物信息學； 趙婧（1996—），女，河南洛陽人，碩士研究生，主要研究方向：數據挖掘、機器學習； 徐久成（1963—），男，河南洛陽人，教授，博士生導師，博士，CCF高級會員，主要研究方向：粒計算、數據挖掘、機器學習； 王欣雅（1997—），女，河南平頂山人，碩士研究生，主要研究方向：數據挖掘、機器學習。

This work is partially supported by National Natural Science Foundation of China （62076089， 61772176，61976082）， Key Scientific and Technological Project of Henan Province （212102210136）.

SUN Lin， born in 1979， Ph. D.， associate professor. His research interests include granular computing， data mining， machine learning， bioinformatics.

ZHAO Jing， born in 1996， M. S. candidate. Her research interests include data mining， machine learning.

XU Jiucheng， born in 1963， Ph. D.， professor. His research interests include granular computing， data mining， machine learning.

WANG Xinya， born in 1997， M. S. candidate. Her research interests include data mining， machine learning.