不同飽水強度灰巖應變特性及劣化損傷本構模型研究
趙恕軻,侯付闖,趙明誠,楊偉瑋,
(1.山東省調水工程運行維護中心平度管理站,山東 平度 266700;2. 陜西中凱恒瑞工程項目管理有限公司,陜西 西安 710055;3. 西安科技大學建筑與土木工程學院,陜西 西安 710055)
0 引 言
隨著地下工程的快速發展,地下滲透水引發的圍巖失穩問題異常突出,特別是我國西南地區,地下水儲存豐富且巖溶分布較為普遍。巖溶區具有“高水壓、多溶洞”的特點,導致地質構造特別復雜,這給富水巖體工程的安全和高效施工帶來困擾。水-巖作用環境下,巖體內部會因水溶蝕作用伴隨微裂隙的萌生、擴展、貫通,使巖體力學穩定性被弱化,最終導致圍巖體失穩破壞[1-2]。然而,高壓滲透水作用又會加劇巖體強度的劣化速度,增加富水隧道的施工風險。因此,探究不同飽水強度下的巖體應力-應變特性和損傷本構模型具有重要意義。
地下巖體賦存于水-巖或水-力耦合環境中,地質構造或外界開挖擾動作用下,經常伴隨著應力的重新分配及變形破壞的發生[2-3],因此飽水作用或滲流作用是影響巖體強度和穩定性最活躍的因素之一。為滿足實際巖體工程需求,國內外學者開展了水-巖或高水壓作用下巖石力學及損傷特性的試驗和理論研究。文圣勇等[3]對不同飽水紅砂巖進行了單軸壓縮試驗并分析了水-巖作用下的力學和聲發射特征;陳再謙等[4]分析了不同滲透壓下灰巖的應力-應變、峰值強度、特征應力、破裂和聲發射特性以及劣化機制;康紅普等[5]通過水力壓裂試驗研究了水力裂縫擴展規律;Vasarhely和Van[6]、Yilmaz[7]開展了相關水-巖耦合試驗,分析了含水率對巖石峰值強度和彈性模量的影響。傅晏等[8]、姚華彥等[9]、Hale等[10]、Apollaro等[11]開展了涉水邊坡巖體在水-巖作用下的物理力學試驗。在理論研究方面,眾多研究[12-13]將統計理論引入到強度模型中,通過建立巖石損傷與微元體強度間的定量關系,提出了多種模擬巖石變形過程的本構模型。為更好地反映巖石全變形過程的損傷規律,楊明輝等[14]、曹文貴等[15]將Weibull分布模型引入到巖石統計損傷本構模型中,從理論方面揭示了巖石軟化過程的損傷演化規律。隨著研究深入,基于Weibull分布的巖石統計損傷本構在模擬巖石壓縮破壞過程的不適用性逐漸凸顯,理論模擬結果與試驗壓密、彈性階段的真實變形特性存在一定差異,如何建立考慮壓密階段對巖體應力-應變特性影響的本構模型是解決該問題的關鍵。
眾多學者通過室內試驗和理論研究對水-巖作用下巖石力學特性進行了探討并建立了本構模型,對本文的試驗設計與模型建立具有重要指導作用。但目前對于水-巖力學特性的問題研究多是基于不同滲透水壓、不同含水率、干濕循環作用下的巖石力學特性展開,對于強制飽水作用下沉積巖的應力-應變特性和本構模型研究較少涉及。為此,本文基于對不同飽水強度處理的灰巖進行的單軸壓縮試驗,分析了灰巖典型的應力-應變特征,并基于損傷力學理論建立損傷本構模型,研究飽水強度對灰巖的物理力學和損傷特性的影響,可為深部富水巖體工程中的水-巖損傷問題的研究提供參考。
1 灰巖力學試驗研究
1.1 試驗材料
試驗材料采用致密性較好的灰巖,主要礦物成分為碳酸鈣、二氧化硅、其他黏土物質,平均含量分別為91%、6.74%和2.26%。巖樣取自廣西柳州地區,巖性均一,多為次生孔隙,屬于低孔隙巖石。干燥狀態下灰巖的電鏡掃描圖像見圖1。

圖1 灰巖電鏡掃描圖像
為滿足試驗需求,根據國際巖石力學測試標準,通過現場取樣、切割、打磨后,制作成直徑50 mm、高100 mm的圓柱體巖樣,端面不平行度小于0.02 mm。試驗考慮了0、3、6 MPa和9 MPa等4種強制飽水狀態,共制作了12個巖樣。由于飽水強度為手動操作,4種實際飽水強度分別為0、2.98、6.04 MPa和9.08 MPa。為保證灰巖材料具有相同的初始含水率,試驗前對所有巖樣常溫下風干24 h。然后,測試試驗灰巖物理力學參數,見表1。

表1 灰巖物理力學參數
1.2 試驗設備及方法
采用RMT-150C巖石力學試驗系統對不同飽水強度下的4組灰巖進行單軸壓縮試驗。試驗設備包括力學試驗機、強制飽水設備。力學試驗機的最大試驗力為600 kN,可實現不同加載速率下的軸向加載試驗;強制飽水設備可對灰巖進行不同強度的飽水試驗,以模擬不同富水環境下巖體的飽水狀態。
試驗方法:①將風干24 h的灰巖試樣分別置于飽水設備中,不同飽水強度下強制飽水12 h,取出后用保鮮膜包裹密封以防止水分散失。②將飽水灰巖試樣兩端磨平,利用毛刷清除兩端面雜物,涂抹耦合劑,然后安裝于力學試驗機上。③在試樣表面安裝應變計,以測試加載過程中的應力-應變曲線。調整好試樣使其處于加載軸線上,為獲得穩定的應力-應變曲線,力學試驗機的應力加載速率為0.25 MPa/s,直到灰巖破壞。
2 試驗結果分析
將試驗數據進行處理,得到不同飽水強度下灰巖的應力-應變曲線。灰巖的典型應力-應變曲線見圖2。從圖2可知,不同飽水強度下的灰巖試樣應力-應變曲線發展趨勢基本相似,總體均經歷了壓縮密實階段(OA階段)、彈性變形階段(AB階段)、裂隙萌生與擴展階段(BC階段)和破壞變形階段(CD階段)。由于強制飽水作用,灰巖強度被顯著弱化,峰值強度隨飽水強度增加而逐漸減小。以9.08 MPa的應力-應變曲線為分析對象,灰巖的階段應力-應變特性如下:
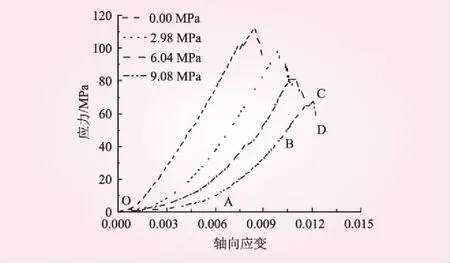
圖2 灰巖的典型應力-應變曲線
(1)壓縮密實階段(OA階段)。隨著軸向應力加載,灰巖內部原生孔隙以及部分新生裂隙逐漸被壓縮至密實,應力-應變曲線表現為緩慢上升。由于灰巖平均干密度為2.68~2.75 g/cm3,故孔隙度相對較小。對于0 MPa的灰巖,其內部孔裂隙很快被壓密,導致壓縮密實階段相對較短。隨著飽水強度的增加,水-巖作用引起內部孔隙數量及尺寸逐漸增大、礦物成分散失,軟化效應使得壓縮密實階段相對延長,灰巖進入彈性變形階段的應變值逐漸滯后。這表明飽水強度對應力-應變曲線的壓縮密實階段具有顯著影響,飽水強度越大,灰巖的壓密階段下凹越明顯,應變路徑越長。
(2)彈性變形階段(AB階段)。隨著軸向應變逐漸增大,內部孔裂隙進一步被壓縮,灰巖的應力-應變曲線開始呈線性增長,隨著飽水強度的增加,應力-應變曲線的線性增長減緩,彈性模量減小。此外,相比較小飽水強度下的彈性變形,飽水強度越大,其彈性變形路徑相對縮短。這是由于經過不同強度的飽水處理后,灰巖內部裂隙水壓加劇了礦物剝離速率,孔隙度增大,不穩定裂隙的擴展規模顯著提高,進而導致灰巖的應變能提前釋放[3]。
(3)裂隙萌生與擴展階段(BC階段)。相比彈性變形階段,該階段的應力-應變曲線表現出上凸特點,且飽水強度越大,應力-應變曲線上凸越明顯。這是由于隨著飽水強度的增加,孔隙水壓加劇了灰巖的劣化,新生裂隙與原生孔隙貫通形成了破壞裂紋,巖石結構逐漸發生塑性變形。隨著軸向應變的發生,灰巖逐漸屈服達到破壞強度。飽水強度越大,灰巖峰值強度越小,相比干燥灰巖,飽水強度為2.98、6.04 MPa和9.08 MPa下的峰值強度分別降低了12.95%、27.56%和38.75%。灰巖峰值強度σc與飽水強度n呈線性關系,即
σc=-4.86n+112.14
(1)
(4)破壞變形階段(CD階段)。隨著應變增大,灰巖內部的大量微裂隙快速交匯貫穿,逐漸形成微裂縫。而隨著軸向荷載的增加,灰巖裂縫快速貫穿形成可見裂紋(見圖3),主裂紋的出現預示著試樣破壞(由于應變計鏈條的遮擋,部分貫穿裂紋未完全顯示)。
對于0 MPa的灰巖,靠近試樣下端面處多處巖塊飛出,試樣表面呈多處巖塊缺失區;而較大飽水強度下的灰巖試樣較少或未出現此現象,這表明飽水強度弱化了灰巖的脆性破壞特性。試驗表明,灰巖試樣破壞形式包括剪切破壞和鼓狀破壞,剪切破壞占總試樣的91.67%,說明飽水強度對灰巖的破壞類型未造成較大影響。
3 不同飽水強度下灰巖劣化損傷特性
3.1 劣化損傷本構方程
Lemaitre應變等效假說[12-13]認為,巖石材料在變形前后應變等價。基于此,建立巖石損傷本構關系為
σ=Eε(1-D)
(2)
式中,σ為有效應力;E為彈性模量;ε為應變;D為損傷變量。
假設巖石為各向同性材料,微元體強度參數F滿足Weibull分布,則巖石材料微元體強度的概率密度函數為
(3)
式中,m和F0為Weibull分布參數。
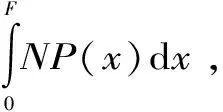
(4)
由式(3)和(4)可知,巖石損傷變量D為微元體強度參數F的函數。對于單個微元體的破壞準則,將式(3)代入式(4)可得Weibull分布的損傷變量D為
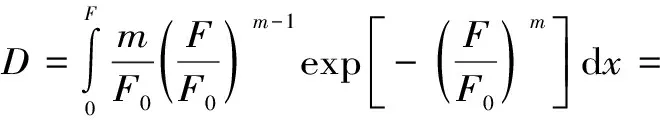
(5)
由式(5)可以看出,巖石損傷本構模型的建立與Weibull分布參數m、F0以及微元強度參數F有關。
3.2 微元強度參數以及損傷本構方程
Drucker-Peager破壞準則具有參數形式簡單、廣泛適用于巖石介質等特點[16]。選擇Drucker-Peager破壞準則作為判斷微元體破壞的判斷準則,則有
(6)
式中,φ為巖石內摩擦角;I1為應力張量的第1不變量;I2為應力張量的第2不變量。I1、I2分別表示為
(7)
(8)
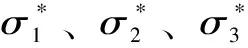
(9)
式中,E、ν分別為巖石彈性模量、泊松比;ε1為應變;σ3為圍壓。
2009年版和2017年版《國家基本醫療保險、工傷保險和生育保險藥品目錄》對比及發展研究 ……………… 沈怡雯等(9):1153
將式(9)代入式(5)后,可得灰巖損傷變量方程
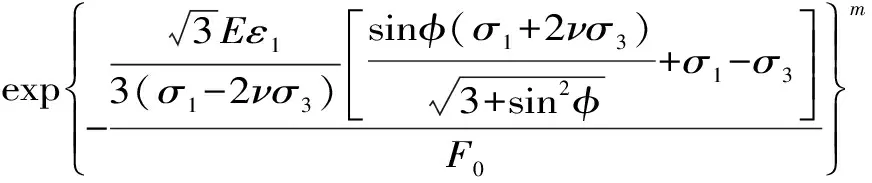
(10)
將式(10)代入式(2),灰巖損傷本構方程為
(11)
3.3 損傷本構方程的求解與驗證
3.3.1 損傷本構方程的求解
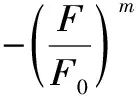
(12)
對式(12)兩邊取對數,可得
ln[lnEε1-ln(Eε1-σ1+2νσ3)]=mlnF-mlnF0
(13)
式(13)表明,本構方程依然包含眾多未知參數。為獲得損傷本構方程的理論解,參考文獻[12]中的研究方法對其進行求解。
假定y=ln[lnEε1-ln(Eε1-σ1+2vσ3)],x=lnF,n=mlnF0,將假定函數y,x,n代入式(13)可得
y=mx-n
(14)
式(14)表明,y為x的一次線性函數,m,n值為與飽水強度相關的參數變量。假設灰巖應力-應變曲線的壓縮密實階段與彈性階段的分界應力為σd,則應力-應變曲線的σ<σd階段和σ≥σd階段對應的表達式為
(15)
通過式(15)分別對應力-應變曲線進行數值擬合,即可得到與飽水強度相關的參數變量m,n值。再將m,n值代入,即可求得宏觀強度參數F01、F02
(16)
3.3.2 損傷本構模型驗證
基于上述分析,利用式(15)分別對應力-應變曲線分段擬合,可得到m,n值;利用式(16)求得參數F01和F02,結果見表2。基于試驗測試,E、ν的平均值分別為18.96 GPa和0.32。
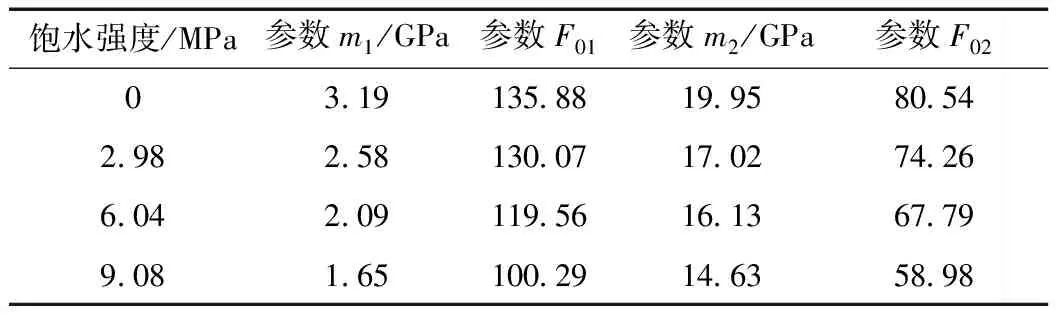
表2 參數m1、m2、F01、F02值
從表2可知,隨著飽水強度的增加,σ<σd階段和σ≥σd階段的參數m1和m2均逐漸降低。相比飽水強度為0 MPa時,2.98、6.04、9.08 MPa條件下的m1分別降低了19.12%、34.45%和48.28%,m2分別降低了14.69%、19.15%和26.67%。隨著飽水強度的增加,參數F01、F02值也呈逐漸減小趨勢,這是由于參數F0反映了巖石的宏觀平均強度[17],這與式(1)和圖2中分析結論一致。
灰巖應力-應變曲線的σ<σd和σ≥σd階段的參數m1、m2、F01、F02隨飽水強度P0的變化趨勢以及數值關系見圖4。從圖4可知,函數參數m1、m2、F01、F02隨飽水強度的增加呈二次或三次函數變化。這是由于飽水強度增大了灰巖含水率,加劇了灰巖成孔速度,導致脆性降低和強度弱化,張二峰等[18]
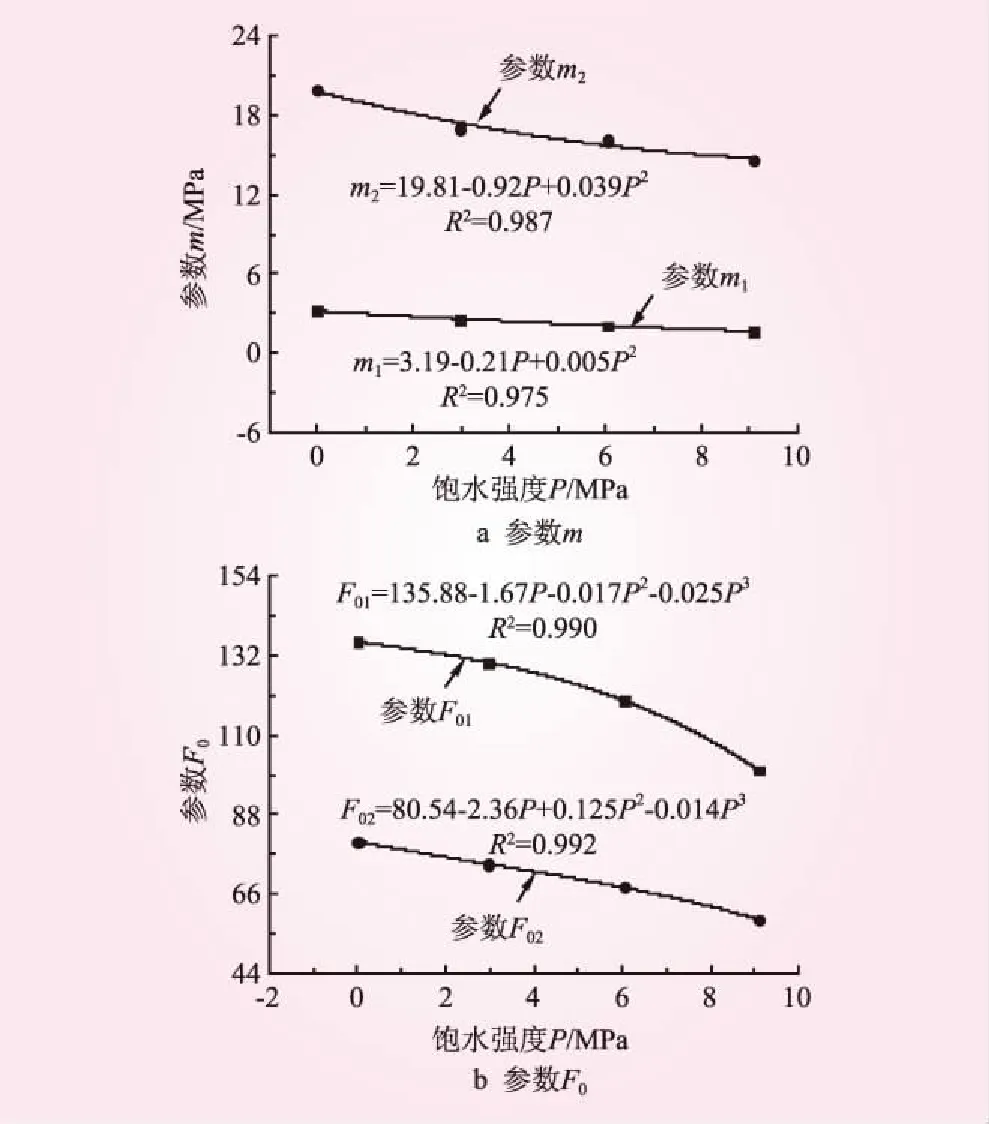
圖4 模型參數m和F0的變化趨勢
也得到過類似結論。結合式(14)和表2中m1和m2可以發現,m1、m2值與應力-應變曲線的瞬態彈性模量具有相同的物理意義。這是由于隨著灰巖飽水強度的增加,巖石內部溶蝕孔隙的數量、尺寸逐漸增加,強度劣化也逐漸明顯。隨著m的降低(飽水強度增加),巖石軟化越明顯。因此,參數m可反映巖石脆性特征以及內部微元強度分布特性,這與何志磊等[19]研究結果具有一致性。
結合式(9)、式(12)及表2可得到不同飽水強度下的灰巖損傷本構關系,不同飽水強度下灰巖應力-應變曲線與模型曲線見圖5。圖5中從左至右4組曲線的實線和虛線分別為0、2.98、6.04、9.08 MPa試驗值與模擬值。從圖5可以看出,不同飽水強度下應力-應變曲線與模型曲線的發展趨勢基本相似,表明所建立的損傷本構模型較好模擬了灰巖的應力-應變特性。飽水強度為0 MPa時,應力-應變曲線與模型曲線重合度較高,這是由于無飽水對灰巖的物理力學特性影響較小,本構模型能夠很好反映灰巖的應變規律。隨著飽水強度的增加,灰巖應力-應變曲線與模型曲線出現較大的偏差,這主要與灰巖內部新生孔隙的分布狀態以及采用分段擬合求解本構參數所產生的誤差有關。由于建立本構模型時充分考慮了壓縮密實階段對灰巖應力-應變特性的影響,應力-應變曲線的σ<σd階段試驗值與模型值具有很好的一致性。
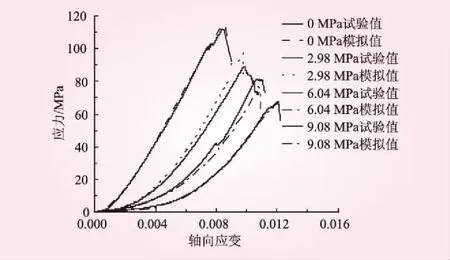
圖5 灰巖應力-應變曲線與模型曲線對比
4 結 語
本文對不同飽水強度的灰巖進行單軸壓縮試驗,研究飽水強度對灰巖力學特性的影響。基于試驗結果分析了典型應力-應變曲線特征,并根據損傷力學理論建立了損傷本構模型。得出以下結論:
(1)灰巖應力-應變曲線經歷了壓密階段、彈性變形階段、裂隙萌生與擴展階段及破壞變形階段;相比低強度飽水灰巖,高強度飽水灰巖的壓密階段相對延長,彈性變形階段相對縮短。飽水強度加劇了灰巖軟化效應,灰巖峰值強度呈線性函數衰減。
(2)飽水作用弱化了灰巖的脆性特征而未對破壞類型造成較大影響。灰巖的破壞類型包括剪切破壞和鼓狀破壞,剪切破壞為灰巖的主要破裂形式。
(3)隨著飽水強度的增加,模型參數m和F0分別呈二次和三次函數降低。模型參數m和F0對揭示灰巖的脆性和強度特征具有重要意義。
(4)對比不同飽水強度下灰巖的應力-應變曲線與模型曲線表明,模型曲線和試驗曲線的吻合度較高,表明建立的損傷本構模型具有可靠性。

