RC框架結構倒塌地震易損性評估

鄭山鎖 溫桂峰 董立國 楊威 劉巍 張藝欣

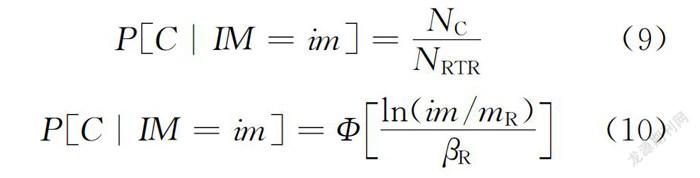
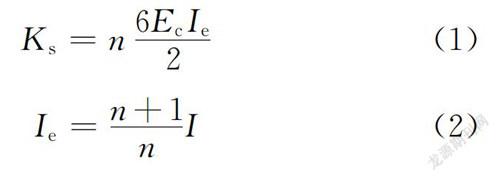
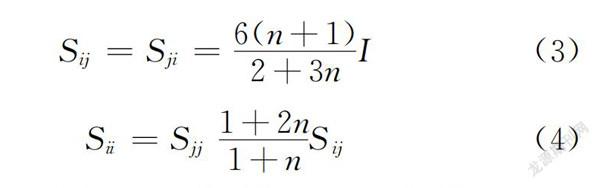
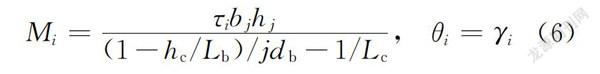
摘 要：為系統評估RC框架結構的抗地震倒塌能力，按照中國現行規范設計了66個典型RC框架結構，基于OpenSEEs平臺建立了考慮節點剪切變形的典型RC框架結構集中塑性鉸模型，并采用IDA分析方法得到各典型結構的IDA曲線與倒塌點;分析設防烈度、層數及跨度對倒塌儲備系數的影響，評估RC框架結構在大震及特大地震下的抗地震倒塌能力。結果表明：按中國現行規范設計的RC框架結構的抗倒塌儲備系數CMR與設防烈度和層數存在負相關關系，而與跨度的相關性較弱;符合現行規范設計的RC框架結構滿足大震不倒的設防要求，但其抵御特大地震作用的能力明顯不足，其中，7.5度設防RC框架結構的抗倒塌能力最弱。

關鍵詞：集中塑性鉸模型;框架結構;倒塌儲備系數;抗倒塌能力;易損性曲線

中圖分類號：TU375.4 文獻標志碼：A 文章編號：2096-6717（2022）05-0177-12

收稿日期：2020-09-02

基金項目：國家重點研發計劃（2019YFC1509302）;國家自然科學基金（51678475）;西安市科技計劃（2019113813CXSF016SF026）;陜西省教育廳產業項目（18JC020）

作者簡介：鄭山鎖（1960- ），男，博士，教授，主要從事工程結構抗震研究， E-mail：zhengshansuo@263.net。

Received：2020-09-02

Foundation items：National Key R & D Program of China（No. 2019YFC1509302）; National Natural Science Foundation of China（No. 51678475）; Science and Technology Program of Xi'an（2019113813CXSF016SF026）; Industrialization Project of Shaanxi Education Department （No. 18JC020）

Author brief：ZHENG Shansuo （1960- ）， PhD， professor， main research interest： earthquake resistance of engineering structure， E-mail： zhengshansuo@263.net.

Seismic collapse fragility estimation of RC frame structures

ZHENG Shansuo， WEN Guifeng， DONG Liguo， YANG Wei， LIU Wei， ZHANG Yixin

（1. School of Civil Engineering; Key Lab of Structural Engineering and Earthquake Resistance， Ministry of Education （XAUAT）， Xi'an University of Architecture and Technology， Xi'an 710055， P. R. China; 2. RBS Architectural Engineering Design Associates Shanghai Office， Shanghai 2000063， P. R. China; 3. Tong Yuan Design Group Co.， Ltd.， Jinan 250101， P. R. China）

Abstract： In order to systematically evaluate the seismic collapse resistance of RC frame structures in China， 66 typical RC frame structures were designed in accordance with the current codes. Based on OpenSEES platform， the lumped plastic hinge model of typical RC frame structures considering shear deformation of joints was established. IDA curves and collapse points of typical structures were obtained by IDA analysis method. Furthermore， effects of building seismic fortification levels， storeys and span on the collapse margin ratio （CMR） were analyzed， and the seismic collapse resistance of the RC frame structure under major earthquakes and severe earthquakes was evaluated. The results show that， the CMR of the RC frame structure designed according to China's current codes has a negative correlation with the seismic fortification levels and stories， but has a weak correlation with the span; the RC frame structure designed in accordance with the current code can meet the fortification requirements of major earthquake， but its ability to withstand the effects of severe earthquakes is obviously insufficient. Among them， the 7.5 degree fortified RC frame structure has the weakest ability to resist collapse.

Keywords：lumped plastic hinge model; frame structure; collapse margin ratio; ability to resist collapse; fragility curves

21世紀初，蘇門答臘地震后，全球進入了地震高發期，中國作為典型的地震多發國家，同樣進入了新的地震活躍期，這為中國防震減災工作帶來了嚴峻考驗。據統計，2008年汶川地震中死亡人數超過6.94萬，受傷人數超過37.4萬;2013年玉樹地震中，死亡人數超過2 600，受傷人數達到9 000多。房屋建筑的倒塌破壞是造成震時人員傷亡的主要原因，因此，控制和預測建筑結構在地震作用下的倒塌是當前防災減災工作的重中之重。

結構倒塌易損性分析方法作為結構性能化抗震理念的重要組成部分，近年來逐步發展成為評估結構抗倒塌能力的主流方法。2009年，美國應用技術委員會（ATC）頒布了第一部結構抗倒塌性能評估標準FEMA P695，建立了基于IDA分析的結構倒塌易損性分析方法。此后，基于該分析方法，Elshear等、錢凱等、Huang等分別對某一RC框架結構進行了抗地震倒塌性能數值模擬分析;Lu等研究了構件尺寸及配筋對RC框架結構抗倒塌能力的影響;蘇佶智等討論了軸壓比、梁柱線剛度比變化對RC框架結構抗倒塌能力的影響;羅開海等對不同設防烈度和不同層數RC框架結構的抗倒塌能力進行了研究;鄧穎婷對不同跨度和不同層數的RC框架結構的抗倒塌能力進行了數值模擬;范萍萍等討論了不同設防烈度和抗震等級對RC框架結構抗倒塌能力的影響;周洲等對中國近年來關于建筑結構地震倒塌易損性方面的研究成果進行了整理和分析，發現現階段中國建筑結構的倒塌風險尚不具有一致性。綜合上述研究結果可以看出，目前學者們雖然已經對建筑結構的抗地震倒塌能力開展了大量研究，但其研究主要集中于探討某一設計參數對結構抗倒塌性能的影響，缺乏對一類建筑結構抗倒塌性能的系統性評價，不利于從整體角度科學認識一類建筑結構的抗倒塌性能。

鑒于此，筆者以符合中國現行設計規范的RC框架結構為研究對象，考慮設防烈度、結構層數及跨度變化對抗地震倒塌能力的影響，設計了66個典型RC框架結構，基于IDA分析方法，分別對其進行抗倒塌性能評估，并剖析了該類結構抗倒塌能力的概率分布，以期為總體認識中國RC框架的抗倒塌性能提供參考。

1 典型結構的設計

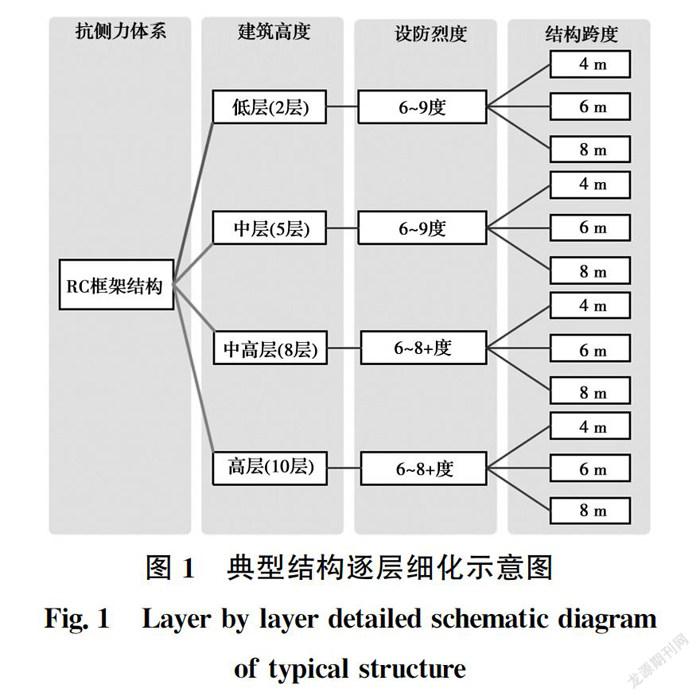
結構設計參數的離散性和所處場地的多樣性是研究結構抗地震倒塌能力時不可忽視的兩個重要因素。ATC-63提出可通過引入體現某一類抗側力體系主要倒塌特征的代表結構，即典型結構來解決結構設計參數的離散性問題。Haselton等指出，典型結構消除了單個建筑物和一類群體結構抗震性能預測間的隔閡。因此，為了研究依中國規范設計的RC框架結構的抗地震倒塌能力，筆者基于ATC-63^[13和Syner-G中關于典型結構的建立方法，結合中國現行設計規范，并綜合考慮設防烈度、建筑高度和跨度3種因素對結構倒塌性能的影響，建立了66個不同設計參數的典型RC框架結構，各典型結構的層數、跨度、設防烈度分布如圖1所示。

針對各典型結構，依據中國現行設計規范，以彈性層間位移角限值為目標，通過反復迭代設計得到各典型結構中構件的幾何尺寸與詳細配筋。為使設計的結構具有典型性，按照如下規則確定結構設計參數及梁柱構件的幾何尺寸：

1）梁截面尺寸：認為每層梁的截面不變，但不同層數梁的截面有所不同，基于規范規定，并滿足工程模數要求及最少截面類型要求，將梁寬取為250 mm，梁高取梁跨的1/10～1/18，同時，考慮到梁截面的實際配筋和施工情況，部分梁的截面寬度可由250 mm增至300、350、400 mm。

2）柱截面尺寸：對于不超過10層的結構，其框架柱應符合規范規定的最小截面尺寸要求，并盡量減少截面類型。

3）結構荷載信息：對于樓面和屋面荷載，參考文獻[16-17]中恒載的簡化取值方法，對樓板、裝修、隔墻、外墻等恒載均折算為樓板恒載輸入，折算后的樓面及屋面恒載取為8 kN/m、活載取為2 kN/m，并考慮周期和樓面活荷載折減;結構的設計地震分組為第二組，場地類別為Ⅱ類;基本風壓為0.4 kN/m、地面粗糙度為C類，基本雪壓為0.3 kN/m。

4）構件設計信息：梁、柱縱筋采用HRB400鋼筋;箍筋采用HPB300鋼筋;2層、5層結構的混凝土強度等級采用C30;8層、10層混凝土強度等級采用C40;樓面及屋面板厚分別取120 mm（跨度6 m和8 m）和100 mm（跨度4 m）;梁、柱構件的保護層厚度取20 mm，板保護層厚度取15 mm。其詳細配筋信息見文獻[18]。

基于上述設計信息，采用PKPM軟件設計了各典型RC框架結構。其中，不同層數6 m跨度典型RC框架結構的PKPM模型如圖2所示。

2 RC框架結構塑性鉸模型的建立

目前，針對RC框架結構的數值模擬方法主要有基于材料本構關系的纖維模型與實體元模型，以及基于截面彎矩轉角關系的集中塑性鉸模型。

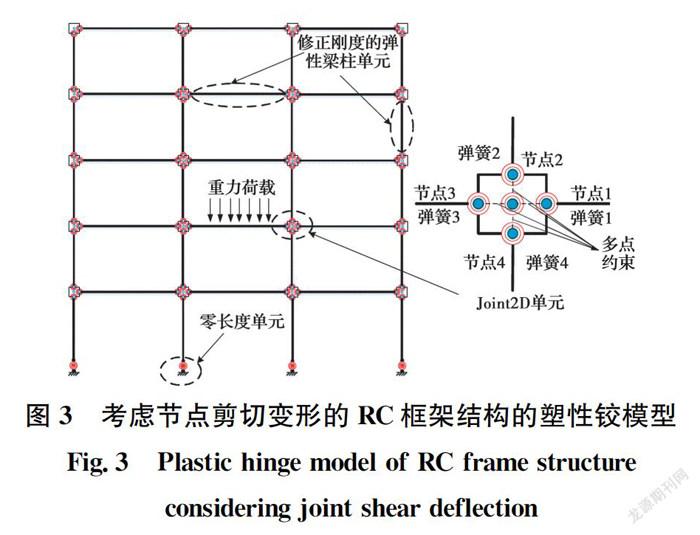
考慮到結構倒塌易損性分析通常以大量IDA分析為基礎，而基于材料本構關系的纖維模型和實體元模型在強非線性條件下計算耗時巨大的現狀，以及在地震作用下RC框架結構構件一般在梁、柱構件端部形成塑性鉸，發生破壞，而構件中部通常保持彈性的特性，采用基于集中塑性鉸模型的RC框架結構的數值建模方法。相對纖維模型和實體元模型，集中塑性鉸模型僅需確定構件端部非線性彈簧單元的力與變形關系就可以較準確地模擬構件的非線性行為，且能夠在保證精度的同時大大降低數值計算成本。鑒于此，基于OpenSEEs平臺建立考慮節點剪切變形的RC框架結構集中塑性鉸模型（如圖3所示），并對該結構模型進行倒塌分析。

2.1 RC框架梁、柱構件數值模型

RC框架結構集中塑性鉸模型將框架梁柱單元簡化為彈性桿單元和端部零長度塑性鉸單元的串聯體系，準確建立梁柱單元集中塑性鉸模型的關鍵是確定中部彈性桿單元和端部塑性鉸單元的力學性能參數。

2.1.1 中部彈性桿單元

由于力學模型的簡化，采用一般的彈性梁柱單元對梁柱集中塑性鉸模型中部的彈性桿進行模擬時，所得到的梁柱塑性鉸模型的剛度將與構件的實際剛度不符，從而導致結構動力特性產生較大誤差，得出錯誤的結構地震反應分析結果。Zareian等針對這一問題，提出了保證集中塑性鉸具有正確剛度的修正方法，該方法通過修正內部彈性單元的截面慣性矩、單元剛度系數和端部塑性鉸單元的剛度予以實現。采用Zareian等建議的修正方法，對梁柱單元集中塑性鉸模型的相關參數進行修正，具體修正方法為

K=n6EI2（1）

I=n+1nI（2）

S=S=6（n+1）2+3nI（3）

S=S1+2n1+nS（4）

式中：E為彈性模量;I為構件的截面慣性矩;L為構件長度;K為彈簧單元初始剛度;I為修正后內部彈性單元（ModElasticBeam2d）的截面慣性矩;S、S、S、S為修正后內部彈性單元的剛度系數;n=K/K，K（K=6EI/L）為內部彈性單元的轉動剛度。在保證集中塑性鉸模型轉動剛度與實際單元剛度相等的前提下，對于修正剛度的彈性單元（ModElasticBeam2d），當n取值越大，該單元的剛度矩陣與一般彈性桿單元的剛度矩陣越接近，但較大的n值容易造成數值計算不收斂，參考Zareian等的建議，取n=10。

2.1.2 塑性鉸單元

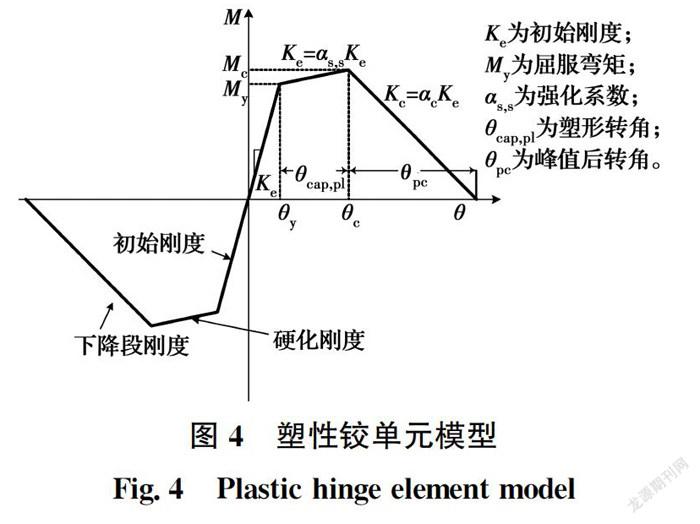
強烈地震作用下，RC框架結構中梁、柱構件端部塑性鉸區的彎矩轉角關系通常具有峰值指向性特點，因此，采用Ligons等提出的具有峰值指向性特點的滯回模型ModIMKPeakOriented描述梁柱塑性鉸區的彎矩轉角關系，如圖4所示。該滯回模型的骨架曲線由6個參數控制，即初始剛度K、屈服彎矩M、強化系數α、塑性轉角θ、峰值后轉角θ和循環能量耗散能力λ。其中，彈簧單元的初始剛度K按式（1）計算確定;對于其余參數的取值，Haselton等基于255個柱試驗數據建立了相應的預測公式并驗證了公式的準確性，筆者采用該預測公式確定塑性鉸單元的力學性能參數。各參數的具體預測公式如表1所示。

此外，由于集中塑性鉸模型同樣采用瑞利阻尼，且僅考慮內部彈性單元的剛度阻尼，不考慮彈簧單元的剛度阻尼，而已對內部彈性單元的剛度進行了修正，因此，為得到正確的剛度阻尼，應對內部彈性單元的剛度阻尼系數進行修正。

β′=n+1nβ（5）

式中：β為剛度阻尼系數;β′為修正后的剛度阻尼系數。

2.2 RC框架梁柱節點域數值模型

嚴格依據中國現行規范設計的RC框架結構均滿足“強節點弱構件”的抗震設計原則，數值模擬分析中通常將節點作為彈性或剛性節點，即不考慮節點破壞。然而，歷次震害資料表明，節點剪切破壞亦是RC框架結構的典型震害，且其破壞易引發RC框架結構倒塌。鑒于此，為有效考慮節點剪切破壞對RC框架結構抗地震倒塌能力的影響，采用Altoontash等提出的二維梁柱節點單元（element Jiont2d）模擬節點剪切變形，建立了考慮節點剪切變形的RC框架結構集中塑性鉸模型，如圖3所示。

Jiont2d節點單元包含4個位于梁柱構件與節點交界面處的轉角彈簧和1個位于節點中心的轉動彈簧，其中，4個轉角彈簧用以模擬梁柱端的轉動變形，中心轉動彈簧用以模擬節點的剪切變形。采用Hysteretic滯回模型模擬節點域剪切恢復力特性，其中，剪切恢復力模型的開裂點、屈服點、峰值點的剪應力和剪應變采用Teraoka等模型計算確定，并根據式（6）轉換為相應的彎矩轉角關系;對于節點域剪切塊的滯回特征取值，參考Altoontash建議的參數值，捏縮點的應力值取為最大歷史應力的25%，應變值取為最大歷史轉角的25%。

M=τbh（1-h/L）/jd-1/L， θ=γ（6）

式中：M、θ為不同受力狀態下節點中心轉動彈簧的彎矩和轉角;τ、γ為節點各受力狀態下的剪應力和剪應變，計算公式見文獻[22];h為柱截面高度;b、h為節點核心區的有效寬度和截面高度;L為上下柱的總高度;d為梁截面高度;L為左右梁的總長度;j為內力矩系數，通常取0.875。

2.3 RC框架結構塑性鉸數值模型的試驗驗證

為驗證上述集中塑性鉸模型建模方法的準確性與合理性，以清華大學完成的縮尺比例為1∶2的3層RC整體框架擬靜力倒塌試驗為參照，根據物理試驗中的構件尺寸、配筋信息及材料的力學性能等參數，按照前述建模方法，確定各梁柱單元的集中塑性鉸模型和節點域剪切模型，按圖3建立該試驗模型的集中塑性鉸數值模型，并進行模擬加載，得到其模擬滯回曲線，進而與試驗結果進行對比，如圖5所示。

由圖5可看出，在模擬得到的在滯回曲線下降段，即結構接近倒塌階段時，與試驗結果的吻合程度較好。模擬滯回曲線也較好地反映了結構近倒塌狀態的強度退化特性，表明基于集中塑性鉸模型的數值建模方法對RC框架結構的倒塌模擬具有良好的適用性，可用于該類結構的抗倒塌性能分析。

3 RC框架結構倒塌易損性分析

3.1 倒塌點定義與IDA曲線

采用前述數值建模方法，分別建立66個典型結構的集中塑性鉸模型，并以ATC-63中推薦的22條遠場地震動作為輸入地震動記錄，分別對各典型結構進行IDA分析，直至引起結構倒塌。其中，每次IDA分析實際上是一次一致激勵（uniform excitation）模式下的動力時程分析。

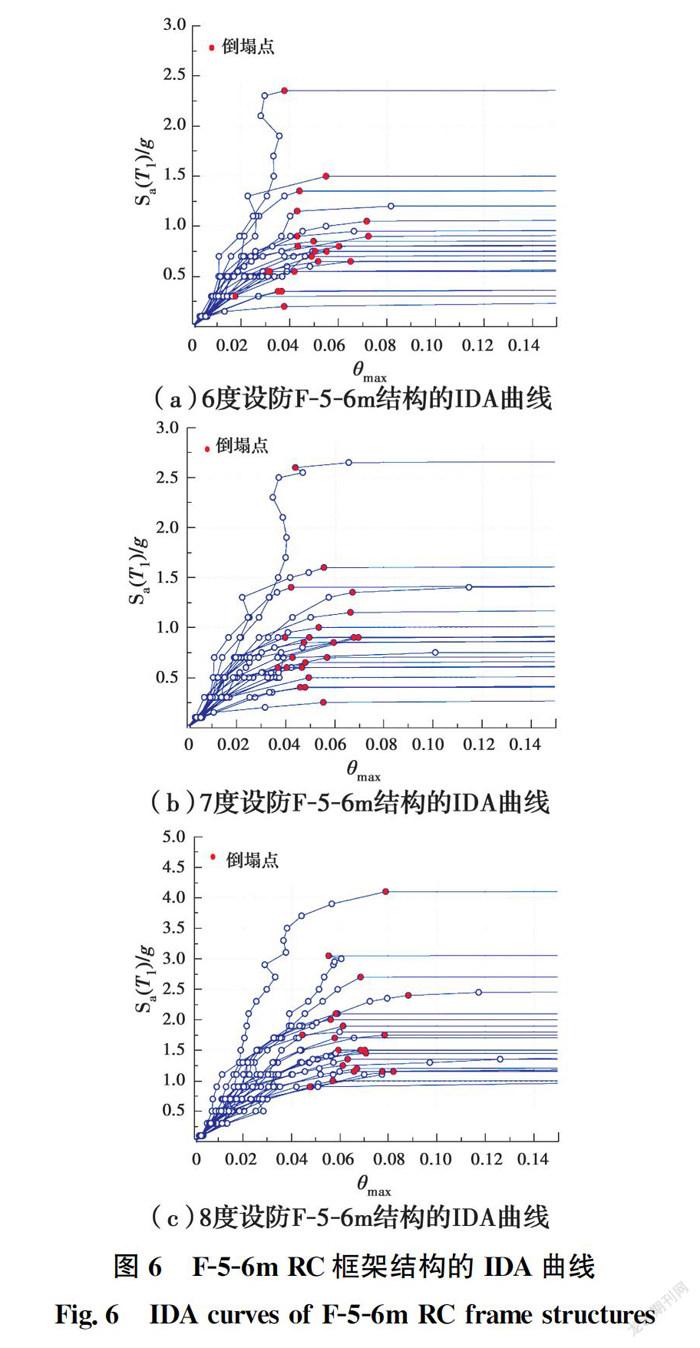
地震荷載作用下，RC框架結構的倒塌行為本質上是一種動力失穩問題，即在微小的地震強度增量下，結構的動力響應將急劇增大。基于此，將地震動強度的微小增量，即引發結構動力響應發生顯著變化的動力失穩點定義為結構的倒塌點，其在IDA曲線上表現為曲線變平的拐點。IDA分析過程中，為了準確捕捉結構的倒塌特征點，并減少地震動調幅次數，借鑒Vamvatsikos等提出的hunt & fill算法對輸入地震動強度進行調幅。既有研究結果表明，采用結構一階周期譜加速度S（T）作為地震動強度指標，可有效降低易損性分析中的不確定性，且考慮到最大層間位移角響應θ與RC框架結構的震損破壞程度具有顯著的相關性，因此，采用一階周期譜加速度S（T）作為地震動強度指標，采用最大層間位移角響應θ作為工程需求參數，繪制各典型結構的IDA曲線。以5層、6 m跨度的典型RC框架結構F-5-6m為例，給出其6、7、8度設防設計的典型RC框架結構的IDA曲線及其倒塌特征點識別結果，如圖6所示。

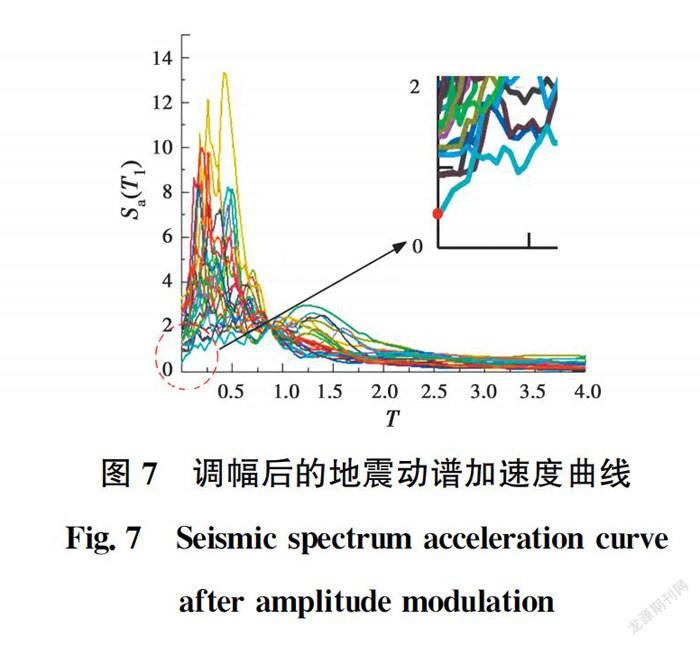
由圖6可看出，最上面一條IDA曲線的數值明顯高于其他曲線，其原因為：以圖6（c）為例，IDA分析時，首先需要對所選地震波進行調幅，使其在結構自振周期T=0.875時的S（T）相等，以S（T）=2.0g為例，給出調幅后輸入的地震動譜加速度曲線，如圖7所示，圖中各曲線與Y軸的交點為輸入地震動的峰值加速度PGA。由圖7可知，相同的S（T）下，存在一條地震動記錄的PGA明顯小于其他地震動記錄的PGA，因此，對于該地震動記錄，需要調幅到更大的S（T），才能使結構發生倒塌破壞，這是圖6（c）中最上面一條IDA曲線的數值明顯高于其他曲線的主要原因。該曲線對應的輸入地震動記錄也是結構可能遭遇的地震動，因此，在后續的概率分析中應該包含這一結果，以反映頻譜特性差異性對結構抗倒塌能力的影響。

3.2 倒塌儲備系數CMR及相關性分析

圖6中各倒塌特征點的縱坐標實際上反映了結構的抗倒塌能力。由于地震動動力特性的差異，結構的抗倒塌能力具有明顯的不確定性，為合理量化結構的抗倒塌能力，FEMA P695建議采用倒塌儲備系數CMR表征結構的抗倒塌能力。CMR反映了結構實際抗倒塌能力與設防需求間的量化關系，其值越大，表明結構的抗倒塌儲備越高，即結構的抗倒塌能力越強。當以一階周期譜加速度作為地震強度指標時，倒塌儲備系數CMR可按式（7）計算。

CMR=S（T）S（T）（7）

式中：S（T）為有50%地震波輸入結構模型使其發生倒塌時對應的地震動強度;S（T）為規范建議的罕遇地震下的地震動強度，可按式（8）計算。

S（T）=a（T）g（8）

式中：a（T）為結構基本周期為T時所對應的罕遇地震下的水平地震影響系數，可按中國現行抗震設計規范所述方法計算確定;g為重力加速度。

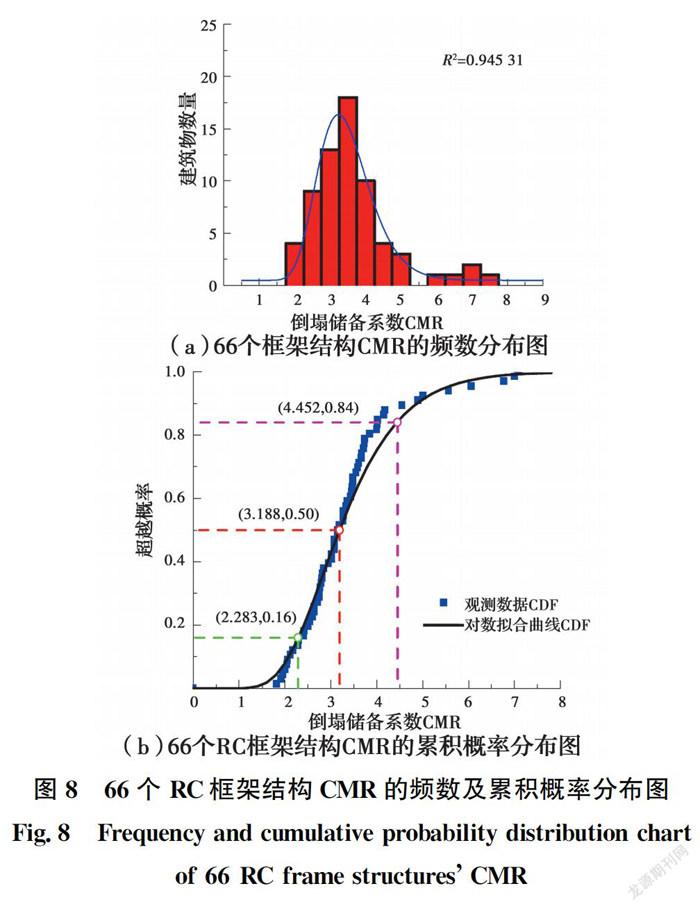
根據式（7）～式（8）以及各典型結構的IDA曲線，計算得到66個典型RC框架結構的倒塌儲備系數CMR，并以此作為RC框架結構倒塌儲備系數的樣本，對其進行統計分析。結果表明，所有典型RC框架結構的CMR均在1.82～7.09范圍內，其均值和中位數分別為3.37和3.16，置信度為95%的置信區間為[3.09，3.65]。根據66個典型結構的倒塌儲備系數CMR的分析結果，給出其頻數分布和累計概率分布結果，如圖8所示。

由圖8可以看出，當采用對數正態分布函數對典型RC框架結構的倒塌儲備系數CMR進行參數擬合時，其擬合優度R大于0.94，表明按中國現行規范設計的RC框架的倒塌儲備系數概率分布基本服從對數正態分布，同時，根據統計分析結果，求出典型RC框架結構倒塌儲備系數CMR概率分布的中位值及對數標準差分別為3.188和0.332，16%及84%分位點為2.283和4.452。該結果符合中國RC框架結構抗倒塌能力儲備情況，可作為初步評估符合中國現行規范的RC框架結構抗地震倒塌能力的依據。

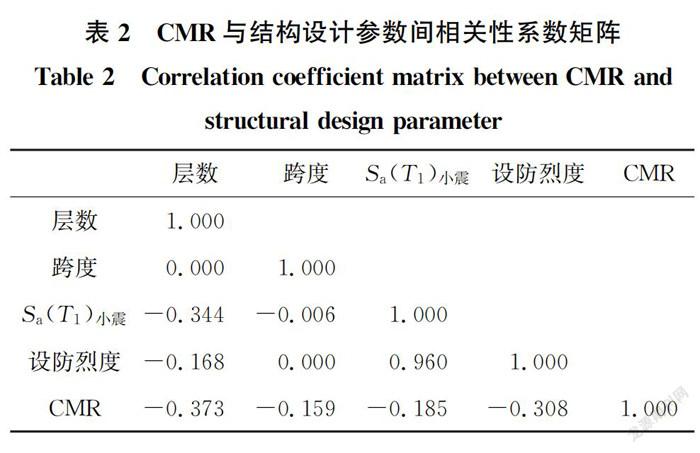
對各典型結構的倒塌儲備系數CMR進行統計分析，得到其與結構設計參數的相關性矩陣，如表2所示。由表2可以看出，CMR和設防烈度間的相關系數為-0.308，與層數間的相關系數為-0.373，即隨著設防烈度和層數的增大，CMR呈下降趨勢;而CMR和跨度的相關性較弱，但兩者仍是負相關，即CMR隨著跨度的增大而減小。

表2中的相關性分析總體上反映了RC框架結構的倒塌儲備系數CMR隨設防烈度、跨度以及層數的變化關系。然而，由于設防烈度、跨度和層數的不同，其CMR變化關系還具有一定的差異性。

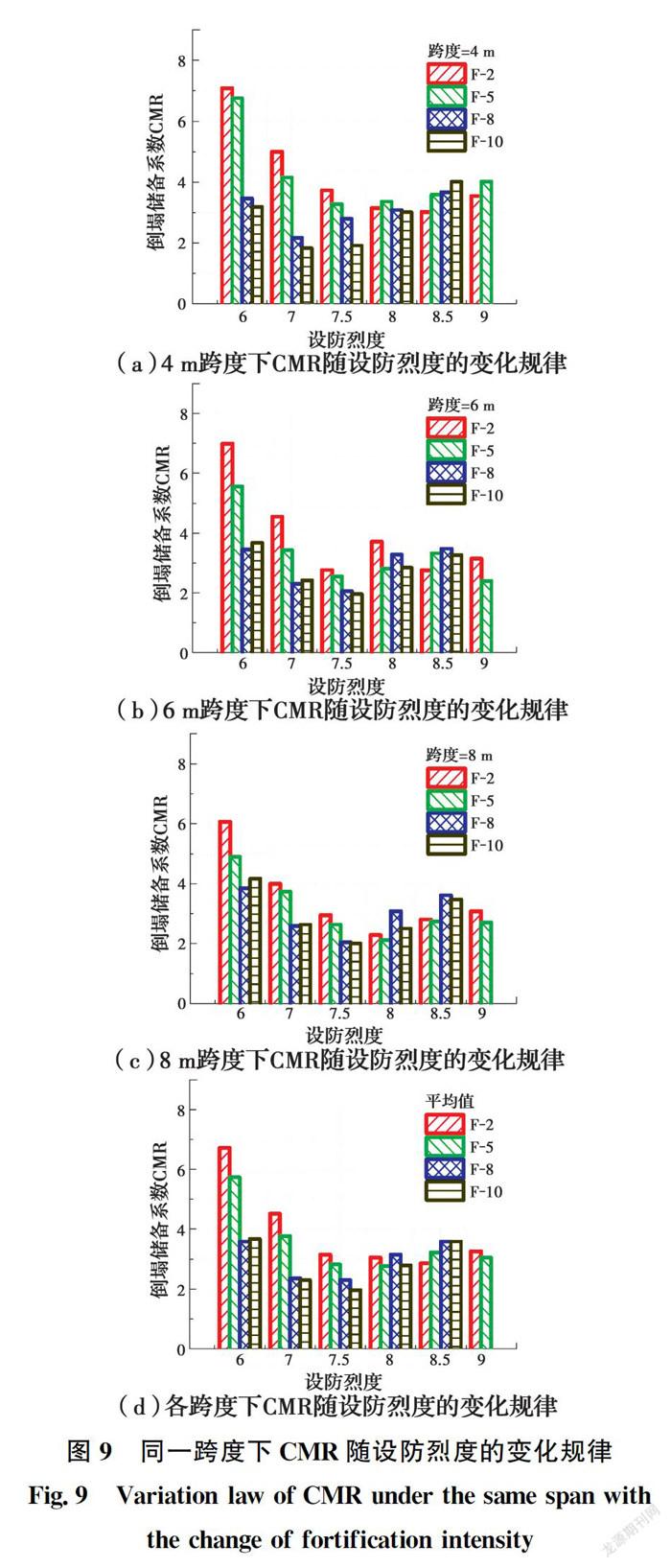
不同層數、相同跨度RC框架結構的CMR隨設防烈度的變化關系如圖9所示。由圖9可以看出，對于跨度為4 m的RC框架結構，2層和5層結構的CMR在8度設防時最小，8層與10層結構的CMR在7度設防時最小;對于跨度為6 m的RC框架結構，各層數結構的CMR均在7.5度設防時最小;對于跨度為8 m的RC框架結構，2層和5層結構的CMR在8度設防時達到最小，8層和10層結構的CMR在7.5度設防達到最小;將不同跨度下結構的CMR取平均值，可以發現各層數結構的CMR平均值在7.5度設防時達到最小值，即依據中國現行規范設計的7.5度設防RC框架結構的抗倒塌能力最弱。

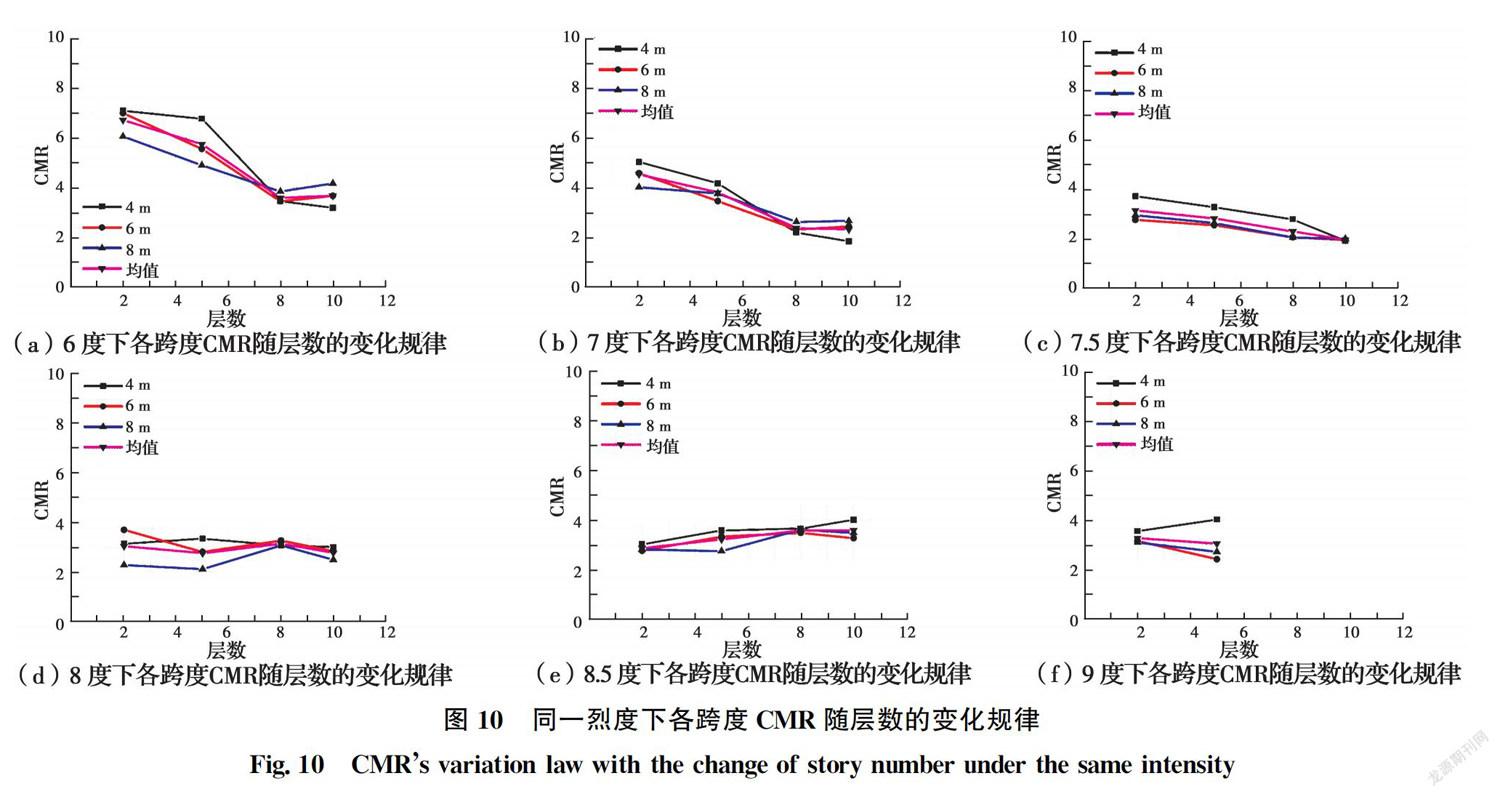
不同跨度、相同設防烈度RC框架結構的CMR隨層數的變化關系如圖10所示。由圖10可以看出，當設防烈度小于7.5度時，RC框架結構的CMR值隨層數增大不斷降低，且其下降速率隨著設防烈度的提高不斷減緩;當結構的設防烈度達到8度時，其CMR開始隨層數增大而趨于穩定，其值約為3;設防烈度達到8.5度時，RC框架結構的CMR隨著層數的增大而略有提升，其值在3～4的區間內變化;設防烈度為9度時，CMR隨層數增加而保持恒定，其值約為3。

產生該現象的原因為：設防烈度較低的RC框架結構設計水平地震力相對較小，對于層數較少的結構，其配筋一般為構造配筋，因而結構實際抗震性能相對理論計算值具有較大富余，但層數較多的結構，其配筋幾乎取決于理論計算結果，因此，低設防烈度下RC框架結構的CMR隨著層數的增加不斷減小，抗倒塌能力不斷降低。當設防烈度增大時，不同層數RC框架結構的配筋均由設計水平地震力控制，其抗倒塌能力的冗余性相當，因此，隨著層數的增多，結構的CMR系數基本不變且略有增大，說明所設計的典型結構具有較一致的地震倒塌風險。

3.3 倒塌易損性分析

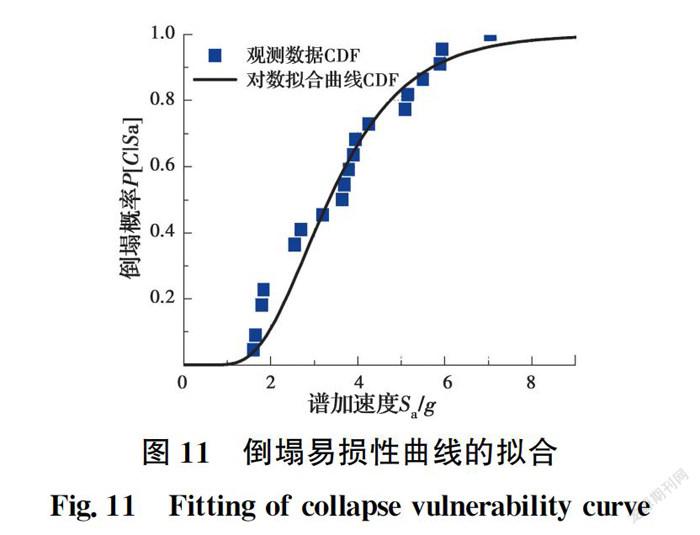
倒塌易損性描述了給定地震強度下結構的倒塌概率，由于結構的倒塌行為本質上是一種動力失穩問題，因此，通常采用基于強度易損性的函數形式構建結構的倒塌易損性模型，具體做法為：根據圖6分析得到的結構倒塌點，采用式（9）所示的頻數統計方法，獲取結構在不同強度地震作用下的倒塌概率，進而采用式（10）對獲取的倒塌概率進行參數擬合，得到連續的倒塌易損性曲線，其分析示意如圖11所示。

P[C|IM=im]=NN（9）

P[C|IM=im]=Φln（im/m）β（10）

式中：N為N條地震動記錄中使結構倒塌的地震動記錄數量;m為結構抗倒塌能力的中位值;β為結構抗倒塌能力對數標準差，當僅考慮地震動的RTR不確定性時，β=β;Φ為標準正態概率分布函數。然而，基于集中塑性鉸模型對RC框架結構進行倒塌易損性分析時，還應考慮建模不確定性對β的影響。Haselton通過分析集中塑性鉸模型中對倒塌預測有影響的各個參數，給出建模不確定性參數β，建議取值為0.5。

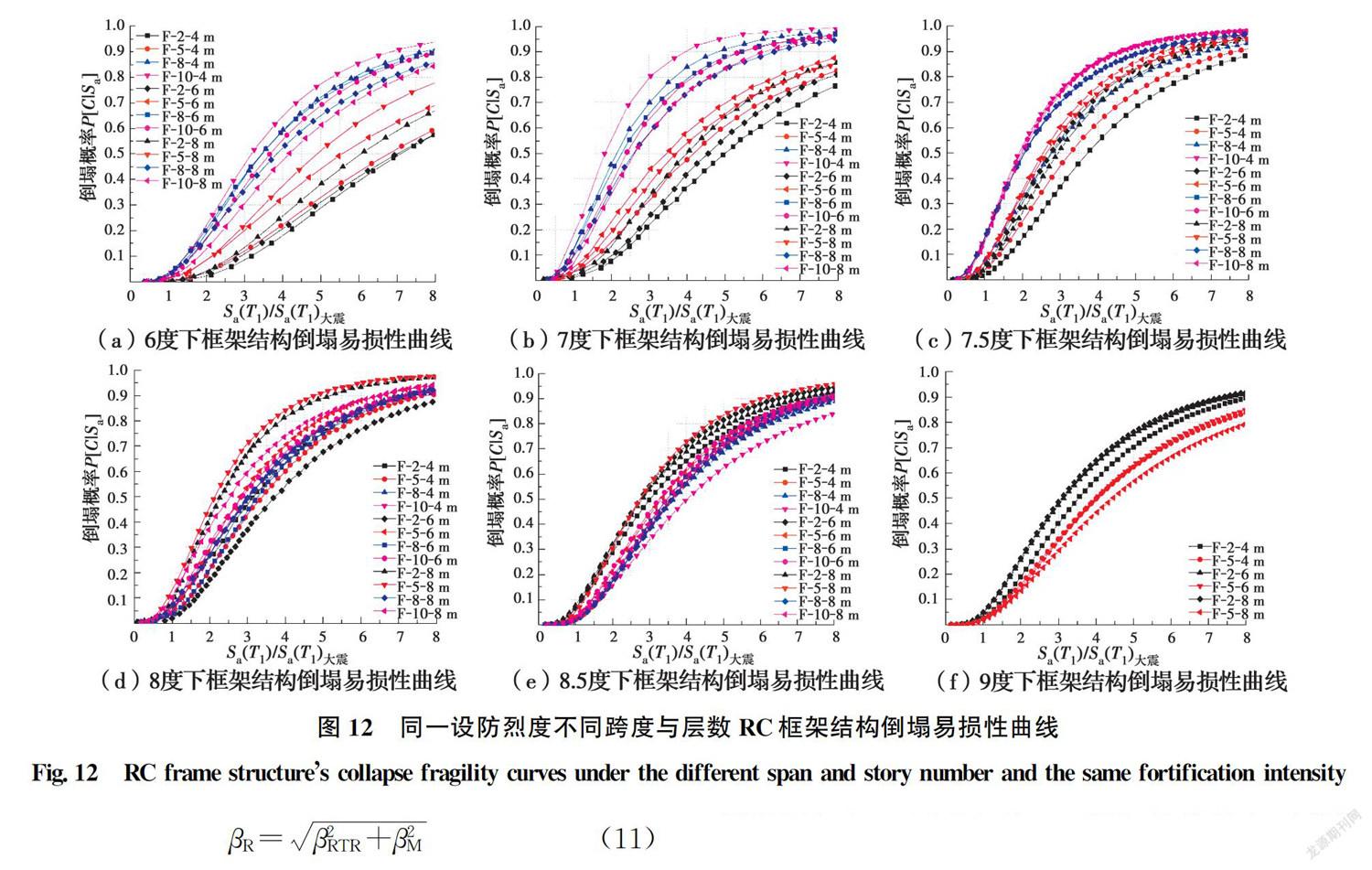
鑒于建模不確定性對結構抗倒塌能力的中位值并無影響，根據式（10）擬合得到各典型RC框架結構抗倒塌能力的中位值m和僅考慮地震動RTR不確定性的β后，進一步取β為0.5，按式（11）計算得到其相應的抗倒塌能力對數標準差β，并帶入式（10），得到各典型RC框架結構的倒塌易損性曲線，其橫坐標歸一化處理，即除以相應大震下的譜加速度S（T）后的結果見圖12。

β=β+β（11）

式中：β值為各結構抗倒塌能力的對數標準差。

3.3.1 大震下結構倒塌概率分析

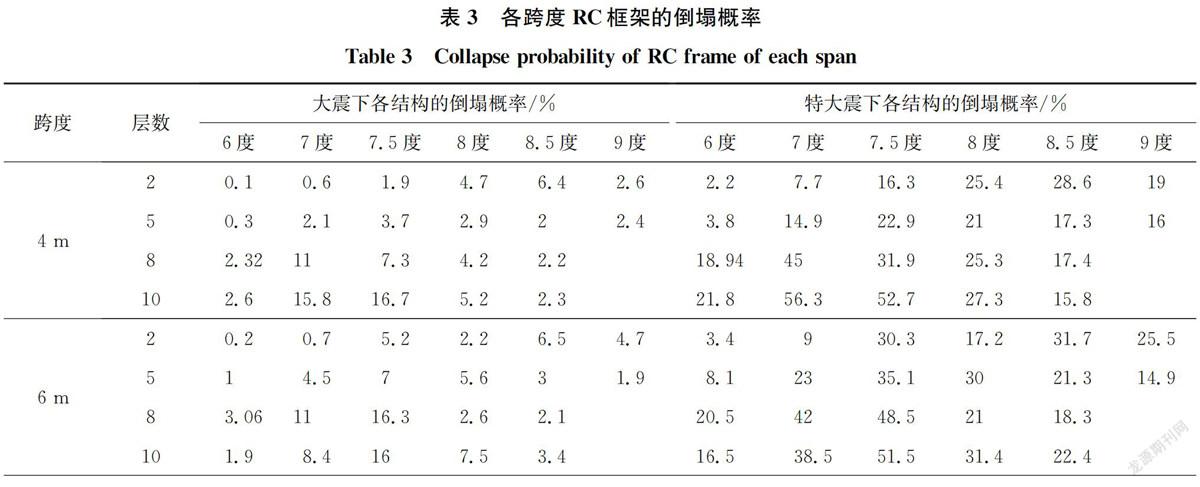
依據上述倒塌易損性分析結果，計算得到各典型RC框架結構在大震下的倒塌概率結果，見表3，并作出大震倒塌概率的頻數及累積概率分布圖，如圖13所示。由表3和圖13可以看出，按中國現行規范設計的典型RC框架結構在大震作用下的倒塌概率分布于[0.1%，16.7%]區間內，其中，84.8%的結構倒塌概率小于10%，15.2%的結構倒塌概率在10%～16.7%范圍內。設防烈度為7.5度和8度的8層、10層結構是倒塌概率在10%以上的RC框架結構的主要群體。相應層數和設防烈度的各跨度典型結構的大震倒塌率平均值列于表3。

由表3可以看出，F-8-7度、F-10-7度的倒塌概率較一致，約為10%，而F-8-7.5度、F-10-7.5度的倒塌概率超過了10%，其余結構的倒塌概率在8%以下。ATC-63報告建議以設防大震下結構倒塌概率不超過10%作為結構達到大震不倒性能要求的標準，由此可以說明，依據中國現行規范設計的RC框架結構具有91%的可靠度，滿足大震不倒的設防目標。

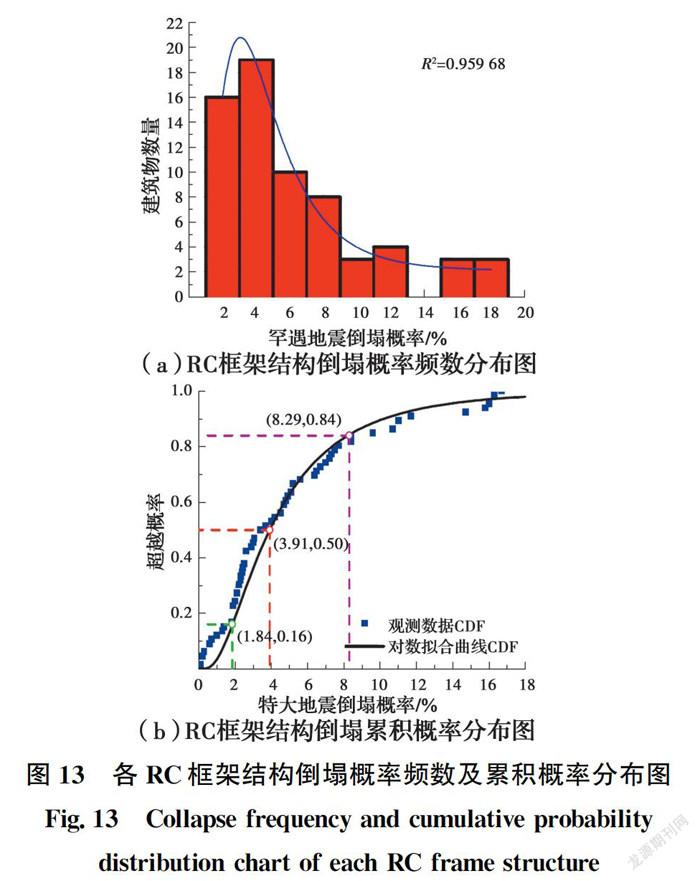
3.3.2 特大震下結構倒塌概率分析 建筑結構在服役年限內可能遭遇超越罕遇地震烈度水平的特大地震，從而帶來巨大的經濟損失和人員傷亡，如2008年汶川地震中，震中大范圍區域遭遇了大于設防烈度標準的特大地震，因此，汶川地震后，中國部分學者提出應該總結和反思上述地震災害的經驗和教訓，在中國的建筑防震設防體系中考慮特大地震的影響。

為明確按中國規范設計的RC框架結構在特大地震作用下的抗倒塌性能，參考文獻[28]，取特大地震的地震強度S（T）=2S（T），計算各典型RC框架結構在特大地震作用下的倒塌概率，見表3，并以此為統計分析對象，作出其特大震倒塌概率的頻數分布及累積概率分布圖，如圖14所示。

由表3和圖14可以看出：在特大地震作用下，設計的66個典型RC框架結構中約87.9%倒塌概率在10%以上，約12.1%倒塌概率在10%以下，其倒塌概率的均值為25.16%，表明依據中國規范設計的RC框架結構抵抗特大震的能力明顯不足。文獻[16]對汶川地震中極震區RC框架結構的破壞情況進行了統計分析，給出了11度下RC框架的倒塌比例為23%，驗證了對RC框架結構在特大震下倒塌概率的計算結果基本準確。

4 結論

基于IDA分析方法，對66個符合中國現行設計規范的典型RC框架結構進行抗地震倒塌性能分析，并剖析該類結構抗倒塌能力的概率分布，得到以下主要結論：

1）符合中國現行設計規范的RC框架結構倒塌儲備系數CMR的分布范圍為[1.82，7.09]，且其與結構跨度的相關性較弱，而與層數和設防烈度均為明顯的負相關關系。

2）不同設防烈度下，RC框架結構的CMR平均值在7.5度設防時達最小值，表明依據中國現行規范設計的7.5度設防RC框架結構的抗倒塌能力最弱。

3）在大震作用下，符合中國現行規范的RC框架結構倒塌概率不超過10%的約有85%，而在特大地震作用下，倒塌概率不超過10%的結構僅占12.1%，表明按照現行規范設計的RC框架結構基本滿足大震不倒的設防目標，但抵御特大震作用的能力明顯不足。

此外，需指出的是，所設計的典型結構場地類型為Ⅱ類，設計地震分組為第二組，其研究成果僅反映該場地條件下結構的抗倒塌性能。對于其他場地條件，應該設計相應的典型結構分別進行分析。

參考文獻：

[1] Quantification of building seismic performance factors： FEMA P-695 [S]. Applied Technology Council for the Federal Emergency Management Agency， Washington， D. C.， 2009.

[2] ELSHAER A， MOSTAFA H， SALEM H. Progressive collapse assessment of multistory reinforced concrete structures subjected to seismic actions [J]. KSCE Journal of Civil Engineering， 2017， 21（1）： 184-194.

[3] 錢凱， 羅達， 賀盛， 等. 鋼筋混凝土框架結構底部相鄰兩柱失效的抗連續倒塌性能研究[J]. 建筑結構學報， 2018， 39（1）： 61-68.

QIAN K， LUO D， HE S， et al. Progressive collapse performance of reinforced concrete frame structures subjected to ground two-column removal scenario [J]. Journal of Building Structures， 2018， 39（1）： 61-68. （in Chinese）

[4] HUANG T C， REN X D， LI J. Incremental dynamic analysis of seismic collapse of super-tall building structures [J]. The Structural Design of Tall and Special Buildings， 2017， 26（16）： e1370.

[5] LU X Z， LIN K Q， LI Y， et al. Experimental investigation of RC beam-slab substructures against progressive collapse subject to an edge-column-removal scenario [J]. Engineering Structures， 2017， 149： 91-103.

[6] 蘇佶智， 劉伯權， 馬煜東， 等. 設計參數對RC框架結構抗倒塌性能的影響分析[J]. 地震工程與工程振動， 2019， 39（3）： 84-98.

SU J Z， LIU B Q， MA Y D， et al. Influence of design parameters on seismic collapse resistant performance of RC frame structures [J]. Earthquake Engineering and Engineering Dynamics， 2019， 39（3）： 84-98. （in Chinese）

[7] 羅開海， 保海娥， 左瓊. 建筑地震倒塌風險分析及設計對策研究（I）——不同設防烈度RC框架結構抗震設計與控制因素分析[J]. 建筑結構學報， 2021， 42（11）： 128-136.

LUO K H， BAO H E， ZUO Q. Analysis of the risk of building earthquake collapse and research on design countermeasures （I）： Seismic design of RC frame structure with different intensity and analysis of seismic design control factors[J]. Journal of Building Structures， 2021， 42（11）： 128-136. （in Chinese）

[8] 羅開海， 保海娥， 左瓊. 建筑地震倒塌風險分析及設計對策研究（Ⅱ）——不同設防烈度RC框架結構的地震倒塌風險統計與分析[J]. 建筑結構學報， 2021， 42（11）： 137-144.

LUO K H， BAO H E， ZUO Q. Analysis of the risk of building earthquake collapse and research on design countermeasures （Ⅱ）： Seismic design of RC frame structure with different intensity and analysis of seismic design control factors[J]. Journal of Building Structures， 2021， 42（11）： 137-144. （in Chinese）

[9] 羅開海， 保海娥， 左瓊. 建筑地震倒塌風險分析及設計對策研究（Ⅲ）——基于統一倒塌風險的建筑抗震設計方法研究[J]. 建筑結構學報， 2022， 43（2）： 13-20.

LUO K H， BAO H E， ZUO Q. Analysis of the risk of building earthquake collapse and research on design countermeasures （Ⅲ）： Seismic design of RC frame structure with different intensity and analysis of seismic design control factors[J]. Journal of Building Structures， 2022， 43（2）： 13-20. （in Chinese）

[10] 鄧穎婷. 地震作用下鋼筋混凝土框架結構抗連續倒塌數值模擬分析[D]. 長沙： 湖南大學， 2017.

DENG Y T. Numerical analysis of collapse-resistant performance of RC frames under earthquake [D]. Changsha： Hunan University， 2017. （in Chinese）

[11] 范萍萍， 陸新征， 葉列平. 7度區RC框架抗地震倒塌能力與加強措施研究[J]. 建筑科學， 2018， 34（11）： 1-7.

FAN P P， LU X Z， YE L P. Study on the collapse-resistant capacity and its strengthen method of RC frames in zones with seismic intensity Ⅶ [J]. Building Science， 2018， 34（11）： 1-7. （in Chinese）

[12] 周洲， 呂大剛， 于曉輝. 基于文獻調研的中國建筑結構地震倒塌風險概率評估[J]. 建筑結構學報， 2020， 41（8）： 1-18.

ZHOU Z， LU D G， YU X H. Probabilistic assessment of seismic collapse risk for building structures in China based on literature investigation [J]. Journal of Building Structures， 2020， 41（8）： 1-18. （in Chinese）

[13] ATC-63. Quantification of building seismic performance factors [R]. Washington DC， 2009.

[14] HASELTON C B. Assessing seismic collapse safety of modern reinforced concrete moment frame buildings [D]. Stanford University， 2006.

[15] PITILAKIS K， CROWLEY H， KAYNIA A M. SYNER-G： Typology definition and fragility functions for physical elements at seismic risk [M]. Dordrecht： Springer Netherlands， 2014.

[16] 清華大學. 汶川地震建筑震害分析及設計對策[M]. 北京： 中國建筑工業出版社， 2009.

Tsinghua University. Structual damage analysis in Wenchuan earthquake and design [M]. Beijing： China Architecture & Building Press， 2009.

[17] JIANG H J， LU X L， CHEN L Z. Seismic fragility assessment of RC moment-resisting frames designed according to the current Chinese seismic design code [J]. Journal of Asian Architecture and Building Engineering， 2012， 11（1）： 153-160.

[18] 楊威. RC框架結構地震易損性研究[D]. 西安： 西安建筑科技大學， 2016.

YANG W. Study on the seismic fragility of RC frame structures [D]. Xi'an： Xi'an University of Architecture and Technology， 2016. （in Chinese）

[19] ZAREIAN F， MEDINA R A. A practical method for proper modeling of structural damping in inelastic plane structural systems [J]. Computers & Structures， 2010， 88（1/2）： 45-53.

[20] LIGNOS D G， KRAWINKLER H. Development and utilization of structural component databases for performance-based earthquake engineering [J]. Journal of Structural Engineering， 2013， 139（8）： 1382-1394.

[21] HASELTON C B， LIEL A B， LANGE S T， et al. Beam-column element model calibrated for predicting flexual response leading to global collapse of RC frame buildings [R]. Peer 03/2007， 03（2008）.

[22] ALTOONTASH A. Simulaiton and damage models for performance assessement of reinforced concrete beam-column joints [D]. Stanford University， 2004.

[23] TERAOKA M， FUJII S. Seismic damage and performance evaluation of R/C beam-column joints [C]//The Second US-Japan Workshop on Performance-Based Engineering for Reinforced Concrete Buliding Structures， Hokkaido， Japan， 2000： 379-390.

[24] 陸新征， 葉列平， 潘鵬， 等. 鋼筋混凝土框架結構擬靜力倒塌試驗研究及數值模擬競賽Ⅰ： 框架試驗[J]. 建筑結構， 2012， 42（11）： 19-22， 26.

LU X Z， YE L P， PAN P， et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure Ⅰ： RC frame experiment [J]. Building Structure， 2012， 42（11）： 19-22，26. （in Chinese）

[25] VAMVATSIKOS D， CORNELL C A. Incremental dynamic analysis [J]. Earthquake Engineering & Structural Dynamics， 2002， 31（3）： 491-514.

[26] 于曉輝， 呂大剛. 考慮結構不確定性的地震倒塌易損性分析[J]. 建筑結構學報， 2012， 33（10）： 8-14.

YU X H， L D G. Seismic collapse fragility analysis considering structural uncertainties [J]. Journal of Building Structures， 2012， 33（10）： 8-14. （in Chinese）

[27] 呂大剛， 周洲， 王叢， 等. 考慮巨震的四級地震設防水平一致風險導向定義與決策分析[J]. 土木工程學報， 2018， 51（11）： 41-52.

LU D G， ZHOU Z， WANG C， et al. Uniform risk-targeted definitions and decision-making of four seismic design levels considering very rare earthquake [J]. China Civil Engineering Journal， 2018， 51（11）： 41-52. （in Chinese）

[28] 陸新征， 施煒， 張萬開， 等. 三維地震動輸入對IDA倒塌易損性分析的影響[J]. 工程抗震與加固改造， 2011， 33（6）： 1-7.

LU X Z， SHI W， ZHANG W K， et al. Influence of three-dimensional ground motion input on IDA-based collapse fragility analysis [J]. Earthquake Resistant Engineering and Retrofitting， 2011， 33（6）： 1-7. （in Chinese）

（編輯 黃廷）