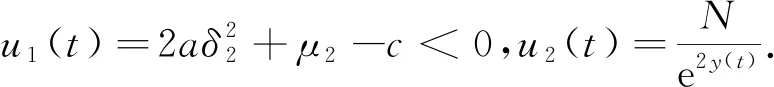污染環境影響的流行病模型動力學行為研究

朝治琴，張啟敏

(寧夏大學 數學統計學院，銀川 750021)

近年來，極端氣候天氣的頻繁發生和工業廢棄物的排放[1]對生態環境質量產生了極大的影響，這些因素也加重了患呼吸道疾病的風險[2]，因此引起了生態、醫療、數學等相關領域學者的極大關注.例如BAKONYI等[3]研究了空氣中的釩、碳元素或可吸入顆粒與呼吸系統疾病惡化之間的相關性.LI等[4]構建了綜合模糊模型研究了空氣污染對哮喘易感的影響.魏妮等[5]討論了大氣中污染物濃度對兒童常見呼吸道疾病的影響.周歷媛[6]給出了空氣污染物濃度越高，呼吸道疾病患者分布越密集，并闡述了隨著空氣污染物濃度的不斷增加，呼吸道疾病患者也會越來越多.此外也有實驗和研究表明室外空氣污染的嚴重程度可以導致呼吸道等病毒感染的風險增加[7-9].

以上學者主要研究了大氣污染與呼吸道疾病的相關性，但未考慮如何設計控制策略來降低污染物濃度的變化和隨機噪聲對流行病的影響.事實上溫度、濕度、沙塵等隨機現象的經常發生都會影響空氣質量[10]，所以為了客觀、全面地了解呼吸道疾病性態，應考慮這些因素對其產生的影響.另一方面控制污染物的排放是預防大氣污染的有效途徑[11]，而對呼吸道疾病的治療則是控制疾病傳播的重要手段[12].因此在模型中加入了控制因素對大氣污染和疾病的干預.本文建立了污染環境中的流行病模型，研究空氣污染的變化和隨機噪聲對呼吸道疾病的動力學行為.

1 模型建立

研究空氣污染和隨機干擾下呼吸道疾病動力學時，通常采用SIS模型的建模方法.其中S是易感染個體數量，I是傳染個體數量.假設總人口數為N，則易感個體的數量可以表示為N-I.呼吸道疾病傳播率函數用β(t)表示，空氣質量指數用F(t)的函數表示.假定疾病的傳播率依賴于空氣污染水平，用β(F(t))表示，這是易感者與受感染個體發生潛在傳染性接觸的速率，它會隨F(t)值不斷變化.因此進一步假定這種關系是線性的，即β(F(t))=βF(t).用μ(t)表示空氣清除率，假定污染物的流入速率為常數c.在模型中，由于β(t)以及μ(t)都會受到隨機擾動的影響，因此將βF(t)和μ(t)分別用β(F(t))+δ1η1和μ(t)+δ2η2來表示，其中η1和η2代表白噪聲，δ1和δ2分別代表白噪聲η1和η2的強度.此外，用u1(t)表示控制污染物排放，用u2(t)表示人為對疾病的干預，例如治療、隔離、媒體宣傳、防護等.根據以上分析，可以得到各因素之間的關系，如圖1所示.

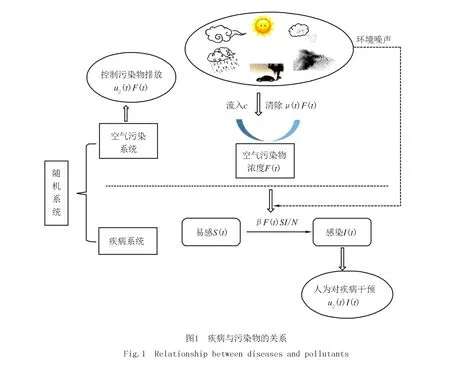
通過圖1，在文獻[13]的基礎上考慮控制向量，得到下列污染環境中的流行病模型：

(1)

這里的B1(t)和B2(t)是獨立的標準布朗運動.其中模型中所涉及的常數N，β，C，δ1，δ2均大于零.

2 有界性與穩定性

對于模型(1)，需進一步研究污染物濃度的有界性和疾病傳播的動力學性質.由于(1)式中的兩個方程是耦合的，首先分析F(t)的性質.在下列分析中，令μ1≤μ(t)≤μ2.

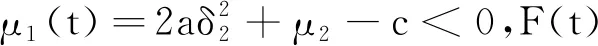
(2)

其中K(p)是依賴于p的常數，與初始值F0無關，即F(t)的p階矩有界.

證明定義V(F(t))=F(t)p，對F(t)∈R+，0

在區間[0,t]上對兩邊同時積分并取期望

可以得到

(3)

根據μ1≤μ(t)≤μ2，(3)式可以寫為

(4)

再令x(t)=E(Fp(t))，可以得到

(5)

對于0

(6)

由方程解的性質可以得到

令

則

所以方程(6)的解為

(7)

定理1給出了系統的有界性，基于這一性質，下面給出系統穩定的條件.

證明取I0∈(0,N)，那么對于所有的I>0，I(t)∈(0,N)成立.只需要對上述定理在區域Γ上給一個證明，這里的Γ={I∶0

(8)

此外

(9)

定義一個C2上的函數V∶[0,∞)×R+→R

(10)

其中k(t)是方程

(11)

的正數解.

直接計算可以得到

(12)

(13)

將(11)式代入(12)式可以得到

(14)

(15)

(16)

對于(16)式，當r→∞時，有

(17)

即上述定理得證.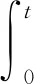

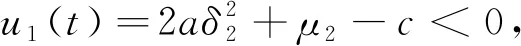
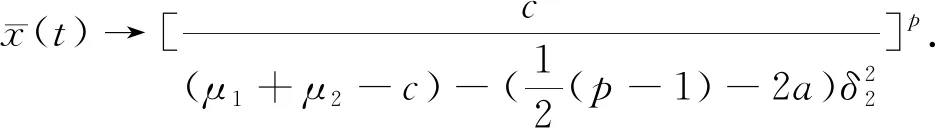
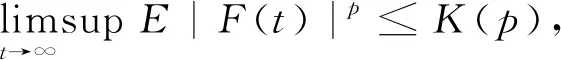
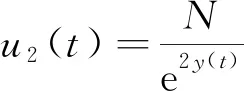
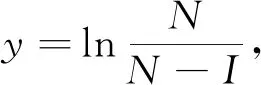
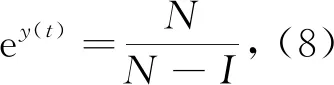
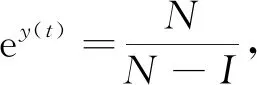
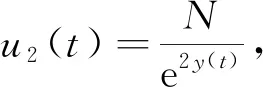
3 總 結