基于ABAQUS仿真的尺寸偏差對密封性能的影響研究*

和建森 郭 飛 吳 凡 黃毅杰 祝世興

(1.中國民航大學航空工程學院 天津 300300；2.清華大學摩擦學國家重點實驗室 北京 100084)

密封結構在現代液壓工業之中起著重要作用[1]。而O形密封圈又是密封結構中最為常見的構件之一，其看似結構簡單，但在現代科學分析過程中想要對O形密封圈進行理論研究是非常困難的。近年來，為探究其密封性能國內外眾多學者[2-15]通過有限元手段做出了諸多努力，通過建立O形橡膠密封圈軸對稱模型，忽略密封結構尺寸偏差影響，借助非線性有限元手段，分析與研究O形圈主密封面在不同工作壓力、不同壓縮率下的接觸壓力變化規律，進而來評判O形密封圈的密封性能優劣。

在實際加工過程中，部件的尺寸偏差是不可避免的。存有不同尺寸偏差的構件裝配在一起組成密封系統進行工作時，橡膠O形圈在使用過程中會產生不同的形變量(即壓縮率不同)，使得密封端面處產生不同的接觸壓力分布，進而影響整體的密封效果。但尺寸偏差對密封結構可靠性的影響研究目前尚未發現。

本文作者為研究結構尺寸偏差對密封性能的影響，采用控制變量法研究了O形圈接觸壓力分布隨尺寸偏差變化的規律；以最大接觸壓力為控制參量，通過不同尺寸組合的力學仿真分析，獲取使最大接觸壓力呈現出最小狀況的最劣尺寸組合，并以泄漏率為評判指標，探究不同配合間隙下(見圖1)O形圈的密封性能，通過對比不同間隙下的泄漏率來分析運行過程中振動對擋板與溝槽配合的影響，從而為進一步提升O形圈的密封性能提供了參考。

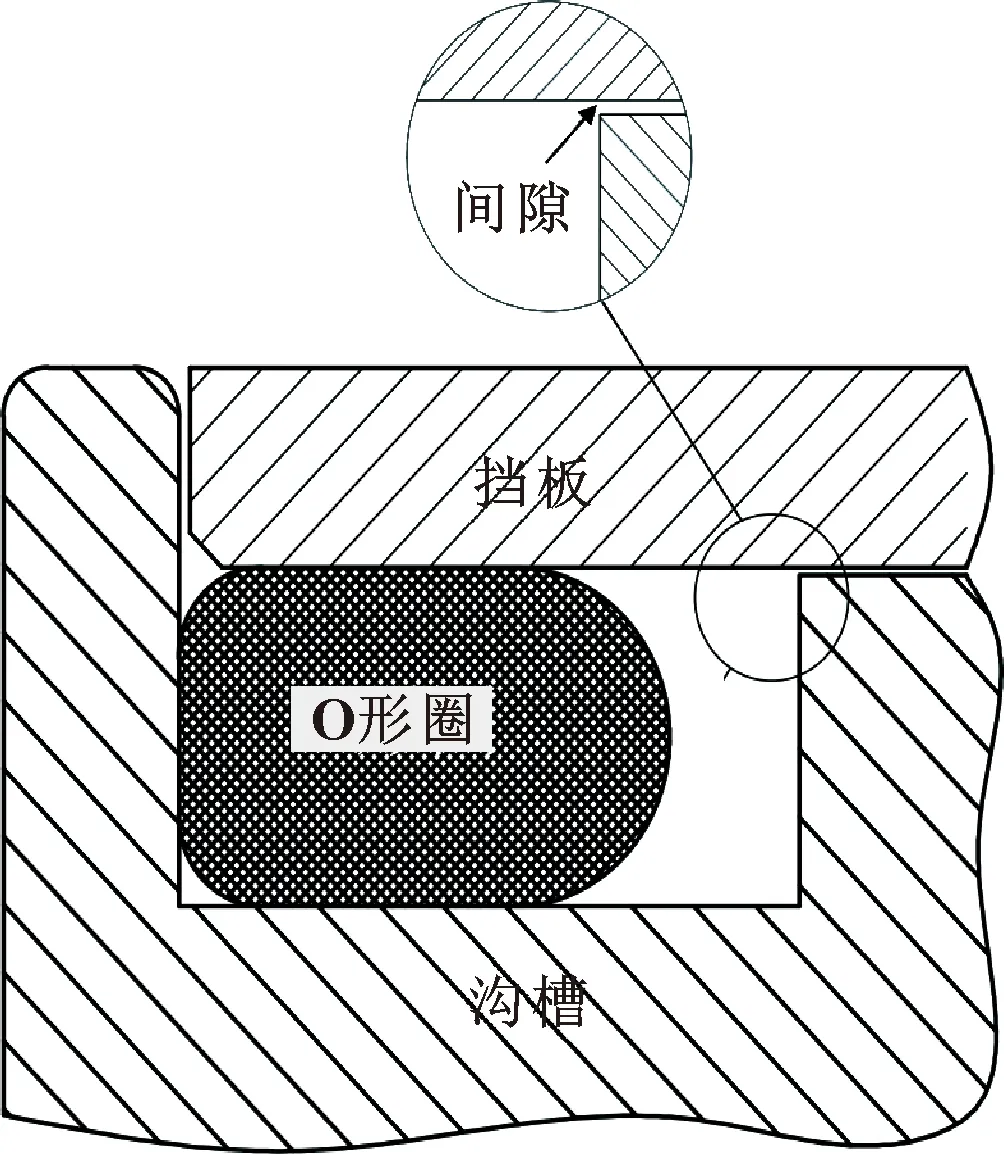
圖1 O形圈密封結構示意Fig.1 Schematic of O-ring sealing structure

1 方法分析

1.1 密封結構分析

圖2及圖3所示分別為O形圈和溝槽結構尺寸。圖中包含的尺寸有橡膠O形圈的截面直徑、內徑，以及溝槽的截面寬度、槽深及槽邊倒圓角5種參數。

文中從O形圈的尺寸偏差及溝槽的尺寸偏差兩方面進行研究，其中O形圈的尺寸偏差考慮截面直徑和內徑偏差2種情況，溝槽的尺寸偏差考慮截面寬度、槽深及槽邊倒圓角的偏差3種情況。采用控制變量法來研究上述不同因素的數值變化對密封界面最大接觸壓力的影響，同時提取相應接觸壓力分布，最終計算泄漏率。

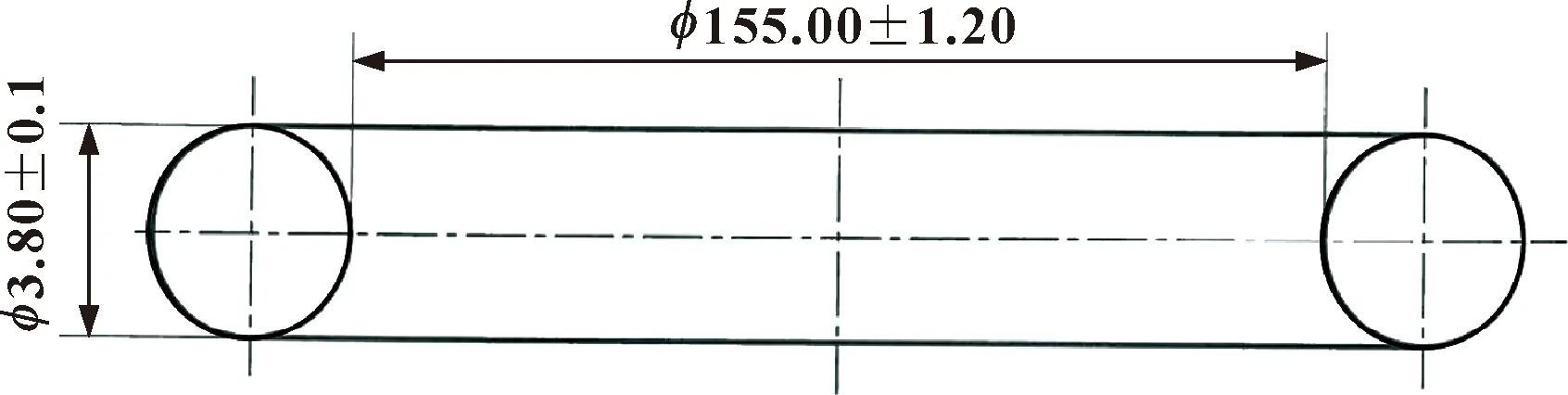
圖2 O形圈結構尺寸Fig.2 Size of O-ring structure

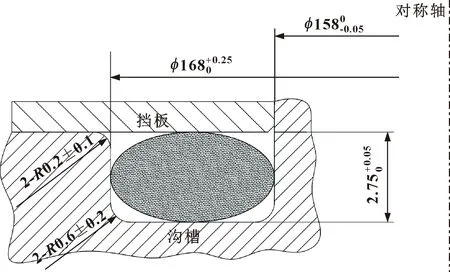
圖3 溝槽結構尺寸Fig.3 Size of groove structure

首先，將公稱尺寸作為初始分析數據，相關參數如表1所示。

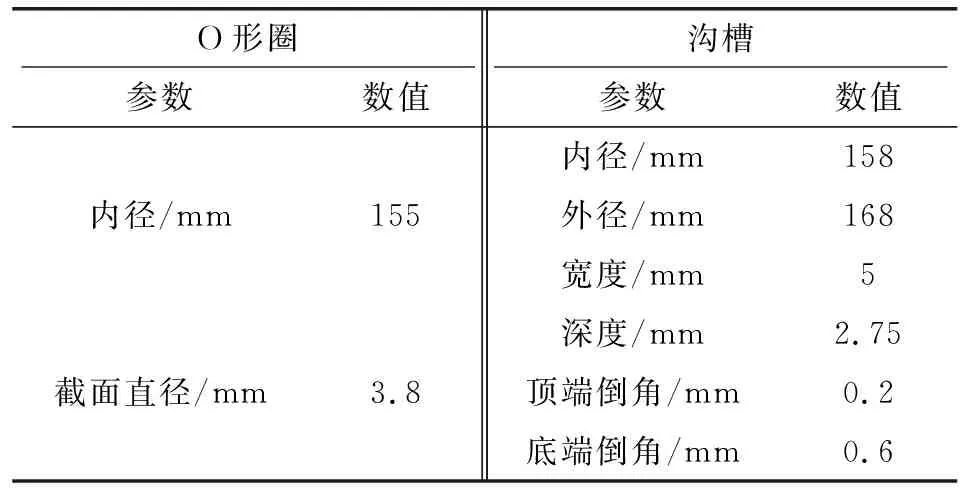
表1 初始裝配結構尺寸Table 1 Initial assembly structure dimensions

將尺寸偏差變量作為對比分析，進行分情形討論。分別從橡膠O形圈的結構尺寸和溝槽的結構尺寸兩方面著手，基于圖2及圖3所示最大尺寸偏差將O形圈和溝槽結構尺寸依次進行變更，所得數據如表2所示。

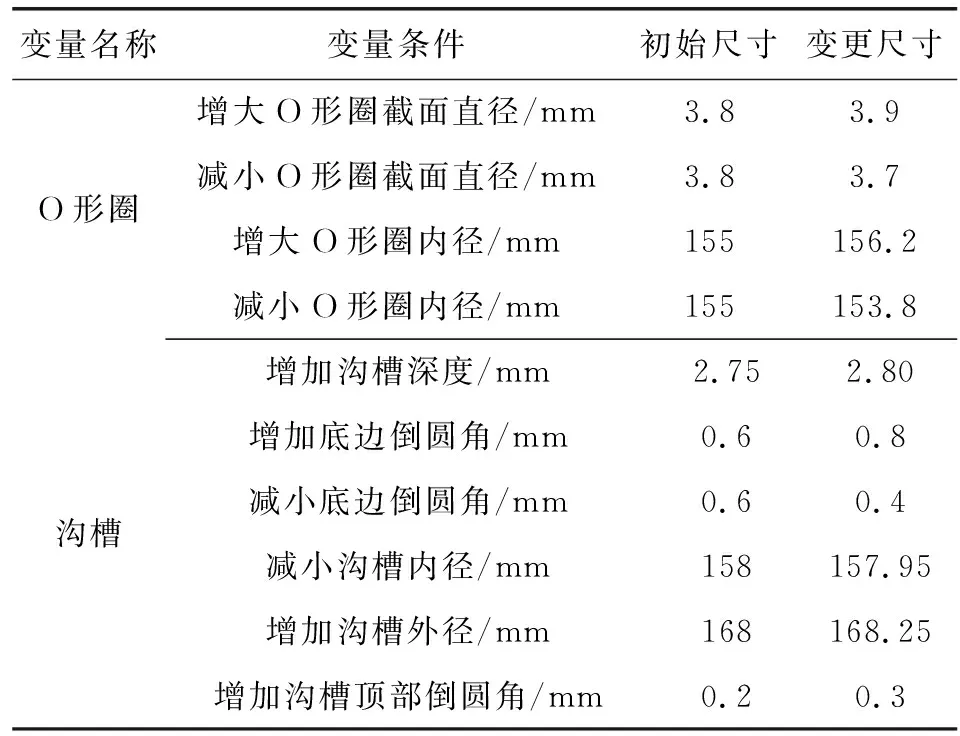
表2 數據變量Table 2 The variable data of structure dimensions

1.2 有限元仿真

文中采用商用軟件ABAQUS進行密封結構的靜力學仿真。

為判斷橡膠O形圈在存有結構尺寸誤差的情況下是否可以可靠使用，對不同尺寸偏差組合的密封結構進行對比分析，選取其中2種情況來展現其變化關系，如表3所示，并基于圖4展示其密封結構。

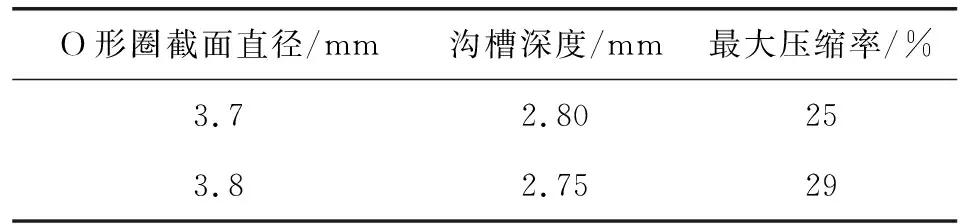
表3 不同尺寸組合的密封結構的壓縮率Table 3 Compression ratio of sealing structures with different size combinations

從圖4可以看出，隨著結構尺寸的變化，橡膠O形圈在實際工作過程中其壓縮率與接觸寬度均有所不同。為提高計算效率，建模采用控制變量法，同時為使得計算仿真更容易收斂，假設密封件具有結構對稱性，取O形圈密封系統進行二維軸對稱幾何建模。

對該模型施加圖5所示的載荷和約束，依據實際使用過程，在第一個分析步中對溝槽施加指向為Ux=2 mm的位移約束，同時在第二個分析步中對擋板施加指向為Uy=2 mm的位移約束，其余約束均設置為固定約束。在第三個分析步中，對橡膠O形圈施加p1=0.4 MPa、p2=0.1 MPa的介質壓力并采用壓力滲透的方式進行模擬。對于溫度場，在第一個分析步中將溫度設置為25 ℃，在第三個分析步中將溫度升至140 ℃，設置橡膠的熱膨脹系數為2.056×10-4℃-1。

圖4 不同尺寸組合的密封結構對比Fig.4 Comparison of sealing structureswith different size combinations

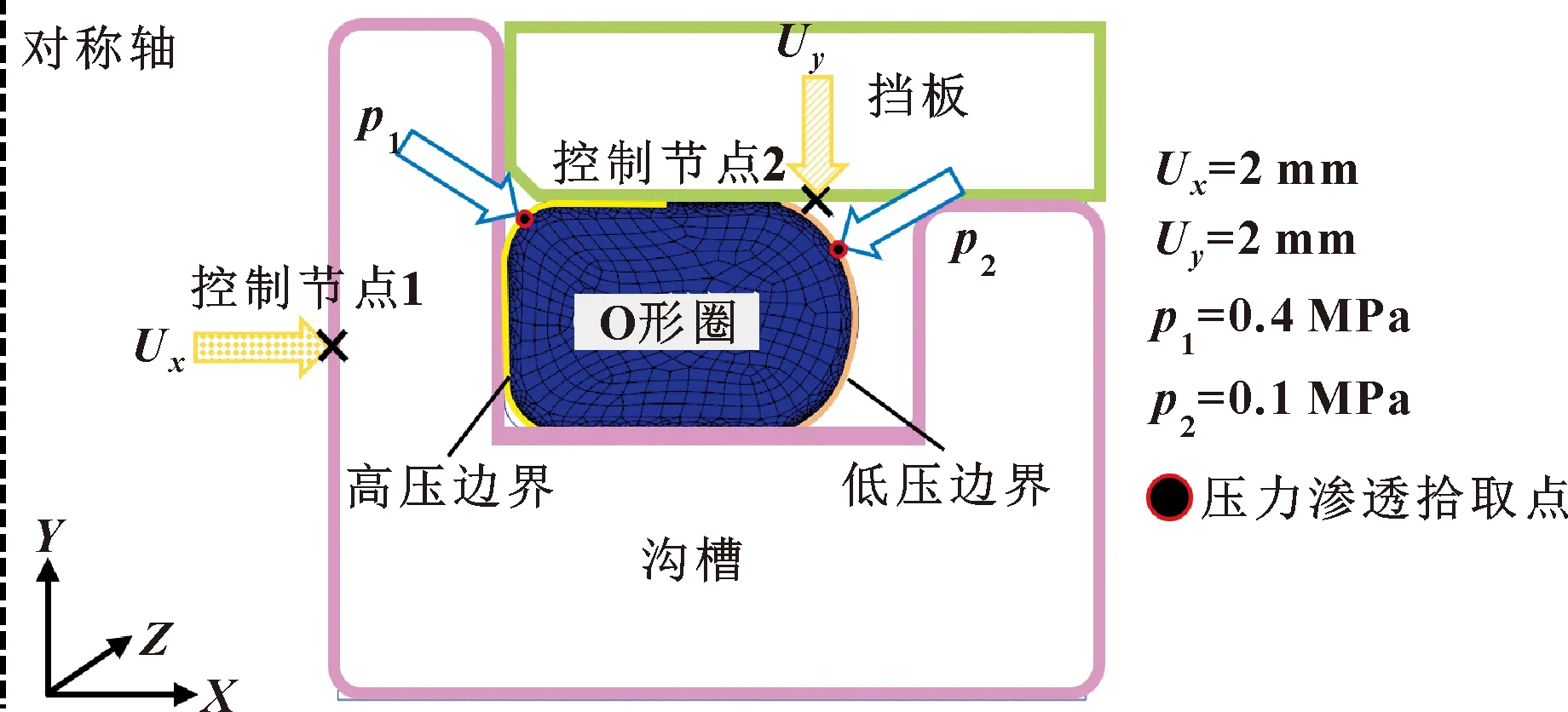
圖5 密封系統幾何模型及施加載荷與約束Fig.5 Geometric model of sealing systemand applied load and constraint

針對氟橡膠的超彈性不可壓縮特性，設置其泊松比為0.49。在仿真計算過程中將氟橡膠單軸拉壓測試應力應變數據導入材料屬性參數中進行本構模型的擬合，擬合結果如圖6所示。

圖6 材料參數擬合Fig.6 The fitting of material parameters

從圖6可以看出Ogden 3階模型曲線與測試數據具有較高的重合度，因此，最終選取Ogden 3階應變能本構模型。Ogden 3階的本構模型表達式為

(1)

式中：U為應變勢能；N為Ogden模型階數，N=3；J為橡膠材料的比體積；μi為材料參數， MPa；αi為無量綱參數；Di為不可壓縮參數，用于表示體積變化；λi(i=1,2,3)為應變張量在3個方向上的主伸長率。

評估數據如表4所示。

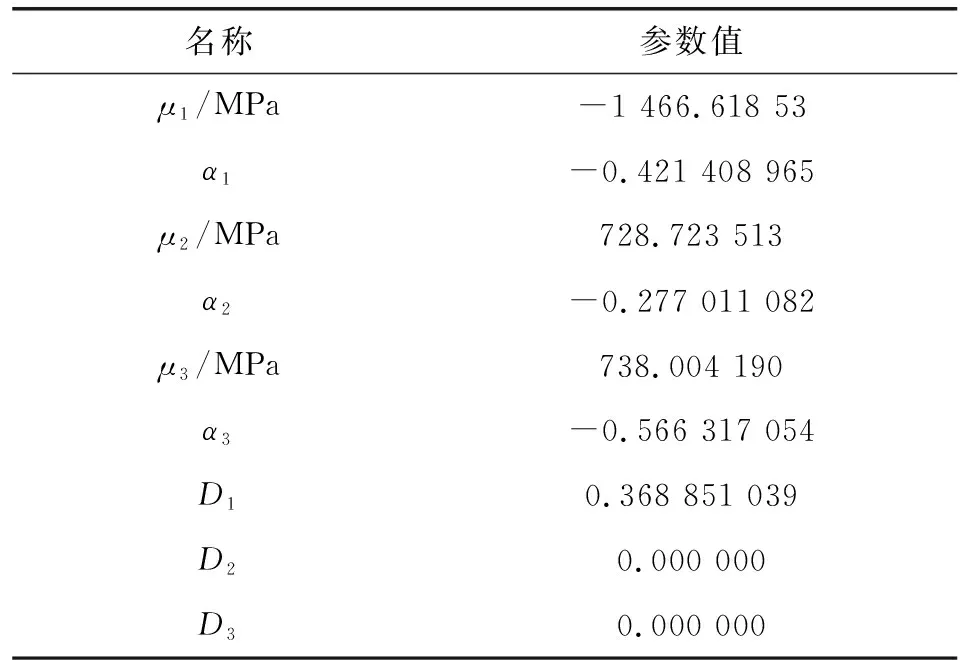
表4 橡膠Ogden 3階性能參數

1.3 密封特性分析

文中基于泄漏率及最大接觸應力來判斷系統密封性能的優劣。由于泄漏率是評估密封系統性能優劣的一項重要指標。因此，文中從計算泄漏率的角度出發，通過提取接觸壓力分布進一步計算泄漏率。在結構選取方面通過仿真來判斷O形密封圈最大接觸壓力的變化情況，提取出最大接觸壓力值均小于其他情況組合下的接觸應力分布，計算泄漏率。依此來判斷系統在存有尺寸偏差的情況下，其密封性能的優劣。

2 結果與討論

2.1 網格無關性驗證

為使仿真結果更具有普適性，文中選取標準狀態下的密封結構進行分析，探究橡膠O形圈在不同網格精度下的最大接觸應力隨間隙變化之間的關系，結果如圖7所示。可以看出，當間隙相同、網格精度的選取在不超過0.08 mm的情況下，改變網格的精度，其最大接觸應力值雖稍有波動，但對于計算結果基本無影響。而當網格精度超過0.08 mm時，此時的網格對最大接觸應力值會稍有影響。根據網格無關性分析，文中采取不同網格精度下獲取的最大接觸應力求取均值的方式固定網格精度為0.02 mm，用于后續的有限元分析。

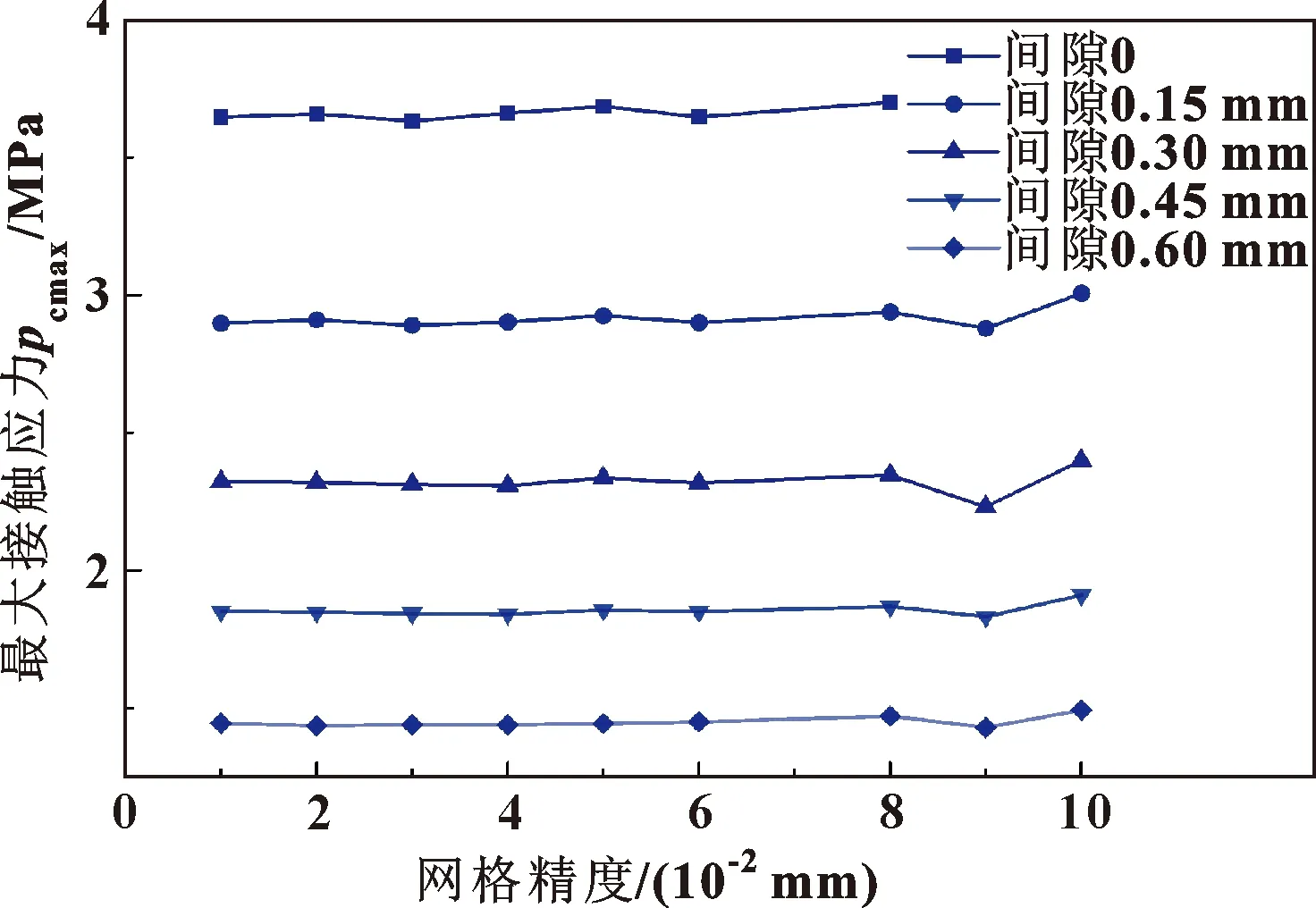
圖7 網格精度與最大接觸應力關系Fig.7 Relationship between mesh precisionand maximum contact stress

2.2 接觸應力分析

2.2.1 O形圈結構尺寸對接觸應力的影響

改變O形圈尺寸，分析了最大接觸壓力隨其的變化關系，如圖8所示。圖8(a)所示為橡膠密封圈內徑恒定為155 mm時，截面直徑變化對橡膠密封圈接觸區域接觸壓力的影響。可以看出，當內徑不變時，截面直徑由3.7 mm增大至3.9 mm其最大接觸應力從3.004 MPa逐漸增大到3.736 MPa。圖8(b)所示為橡膠密封圈截面直徑恒定為3.8 mm時，內徑變化對橡膠密封圈接觸區域接觸壓力的影響。可以看出，當截面直徑保持不變時，內徑由153.8 mm增大至156.2 mm其接觸壓力最大值從3.38 MPa逐漸增大到3.686 MPa。因此，在保證其他因素不變的前提下，單一增大O形圈的截面直徑或內徑，其密封端面的最大接觸壓力呈現增大的趨勢。

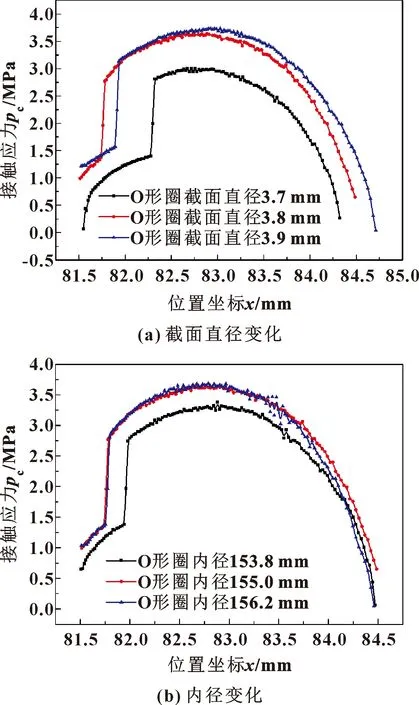
圖8 O形圈尺寸變化與接觸壓力分布關系Fig.8 Relationship between O-ring size change and contactpressure distribution:(a)section diameterchange;(b)inner diameter change

2.2.2 溝槽結構尺寸對接觸應力的影響

圖9所示為其余結構尺寸保持不變的情況下，接觸壓力隨溝槽深度的變化關系。

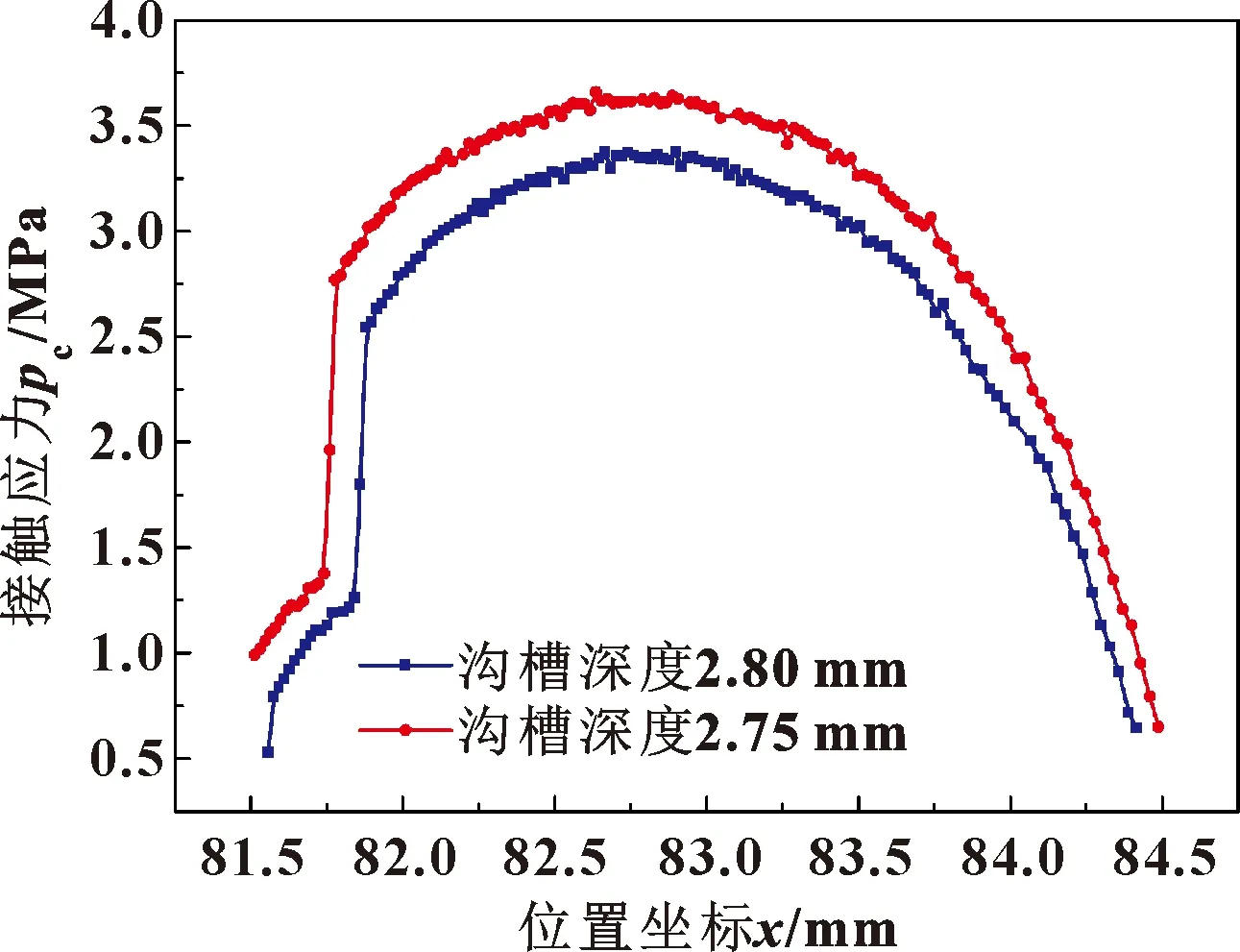
圖9 溝槽深度變化與接觸壓力分布關系Fig.9 Relationship between groove depthand contact stress distribution

由圖9可以看出，當溝槽深度為2.75 mm時，其對應的最大接觸壓力為3.658 MPa；而當溝槽深度增加至2.80 mm時，其對應的最大接觸壓力減小為3.375 MPa。這表明隨著溝槽深度的增大，橡膠O形圈壓縮量降低，其對應的最大接觸壓力減小。

圖10所示為溝槽倒圓角的改變對接觸壓力的影響。由圖10(b)可以看出，當底部倒圓角不變時，頂部倒圓角的變化對最大接觸壓力沒有影響；當頂部倒圓角不變而底部倒圓角發生改變時，由于溝槽底部倒圓槽壁與密封圈之間發生接觸(見圖11)，接觸壓力增加，如圖10(a)所示。

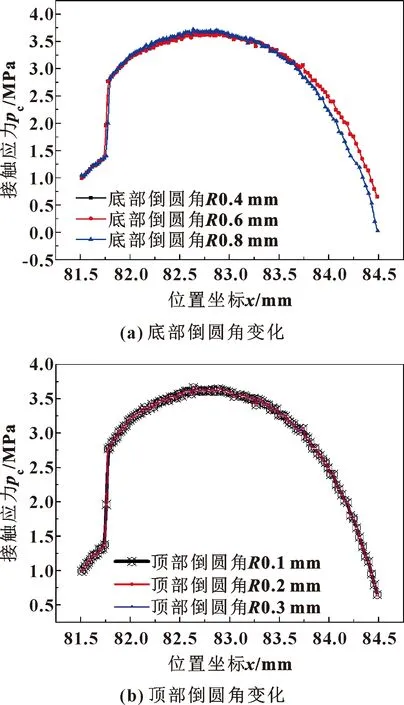
圖10 溝槽倒圓角變化與接觸壓力分布關系Fig.10 Relationship between groove fillet change andcontact stress distribution：(a)bottom filletchange;(b)top fillet change

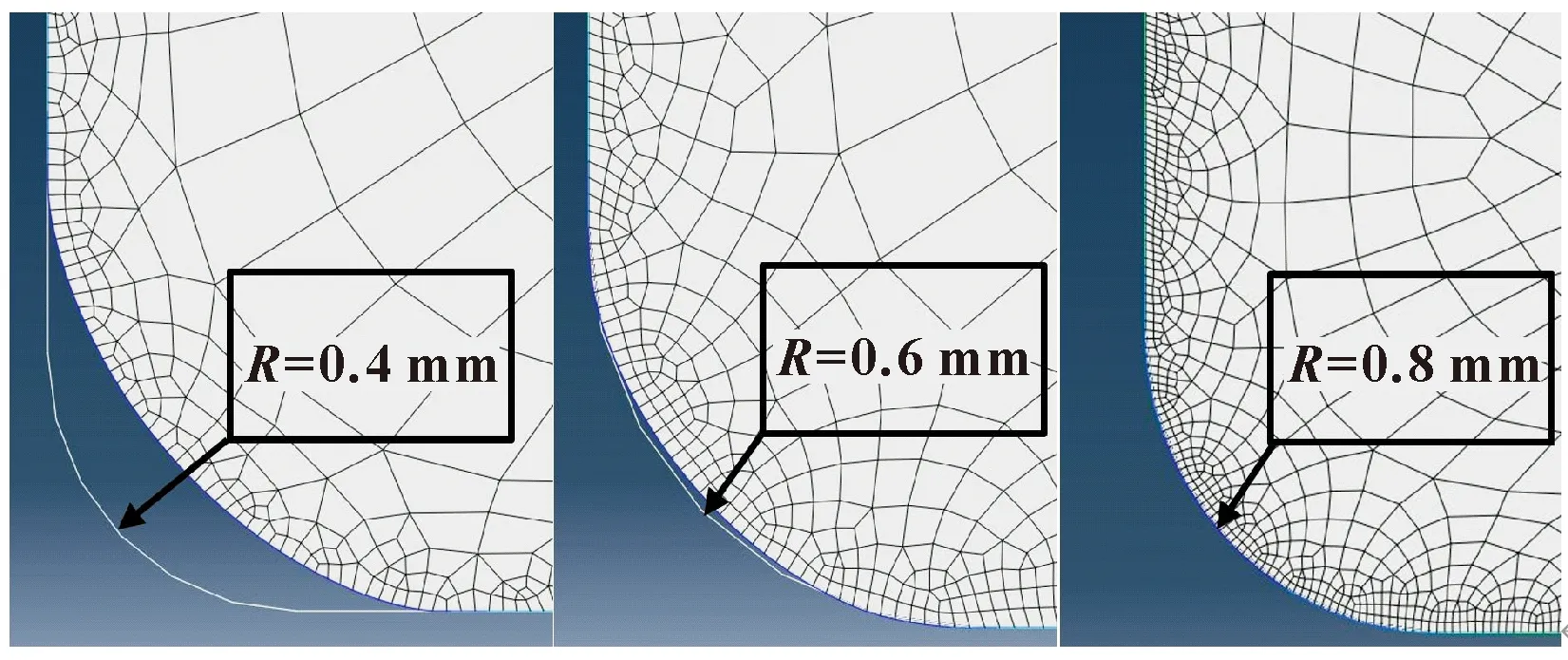
圖11 底部倒圓角仿真示意Fig.11 The fillet simulation of bottom

圖12所示為溝槽內外徑變化對接觸壓力分布的影響。可以看出，隨著溝槽內徑的減小，橡膠密封圈的最大接觸應力由3.658 MPa減小至3.645 MPa，發生微弱變化；而當外徑發生變化時，接觸壓力分布曲線基本一致。產生這種現象的原因是在工作過程中，橡膠密封圈本身在低介質壓力的作用下與溝槽外徑內壁不發生接觸，而溝槽內徑的改變會使得密封圈的徑向壓縮率發生改變。文獻[12]也表明壓縮率越大，最大接觸壓力也越大。

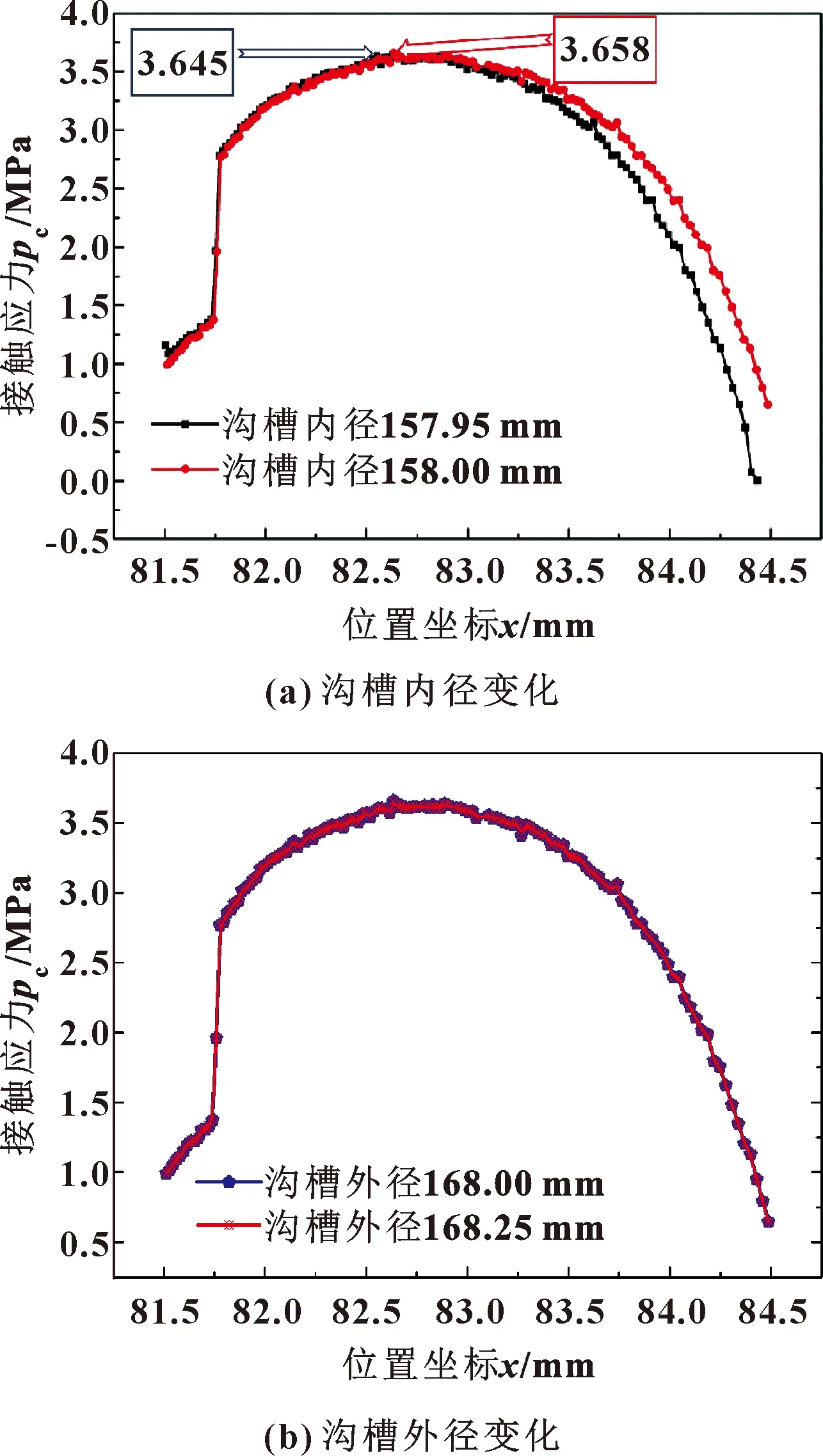
圖12 溝槽內外徑變化與接觸壓力分布關系Fig.12 Relationship between inner and outer diameter changeof the groove and contact stress distribution:(a)inner diameter change of the groove;(b)outer diameter change of the groove

2.3 密封性能分析

在實際工況下由于振動的影響，溝槽與擋板之間便會形成間隙(如圖13所示)，因此，文中分別取間隙值為0、0.15、0.3、0.45、0.6 mm進行泄漏率的計算。

基于2.2節分析結果，將呈現最大接觸壓力減小的情況進行組合，如表5所示。

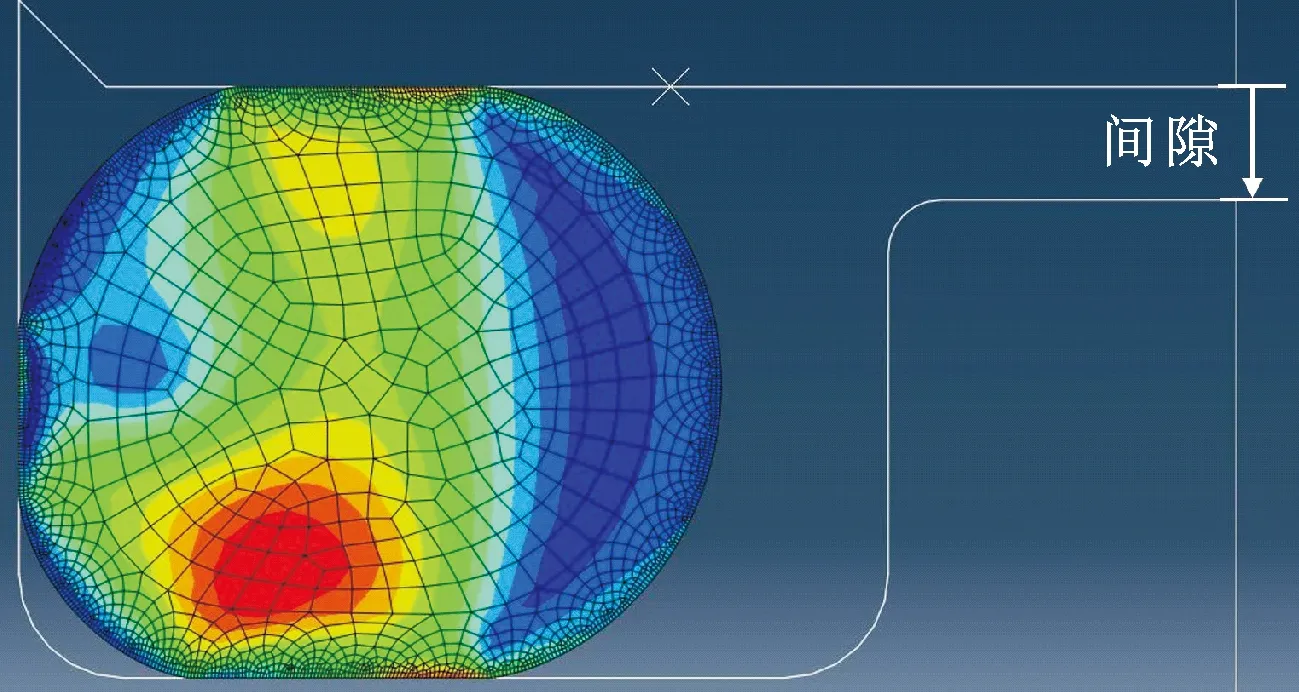
圖13 間隙仿真Fig.13 The simulation of clearance

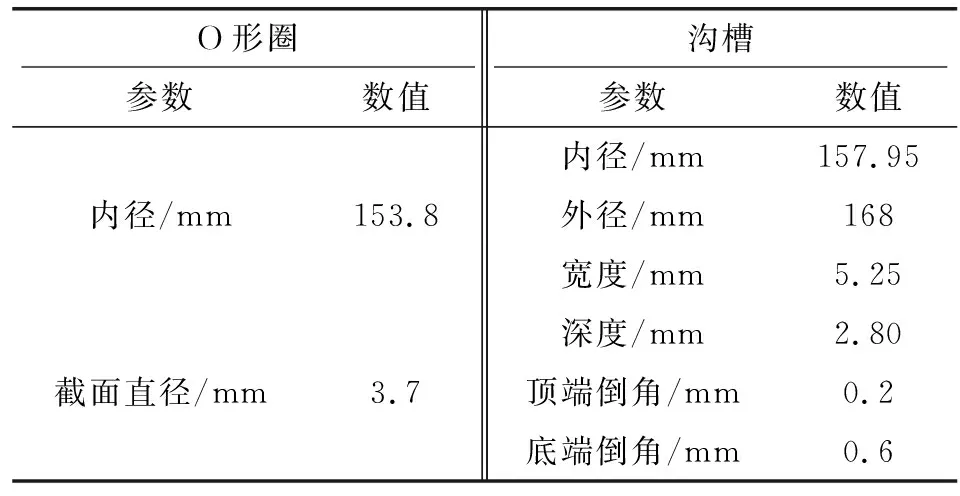
表5 最大接觸壓力值最小時的密封尺寸組合Table 5 Size combination of sealing with minimum maximum contact pressure

將表5中數據導入有限元中進行仿真分析，將不同間隙下的接觸壓力分布進行提取，如圖14、15所示。

圖14和15所示為接觸應力隨兩部件間隙的變化關系。通過對比圖14與圖15可知，當兩者都處于最大壓縮狀態時，最劣尺寸組合的密封結構的最大接觸壓力遠小于標準狀態下。說明在該狀態下最劣尺寸組合的密封結構發生泄漏現象的概率要遠高于標準狀態下。

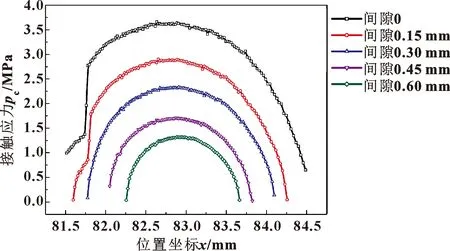
圖14 標準狀態下接觸壓力分布與間隙關系Fig.14 Relationship between contact pressure distributionand clearance under standard condition

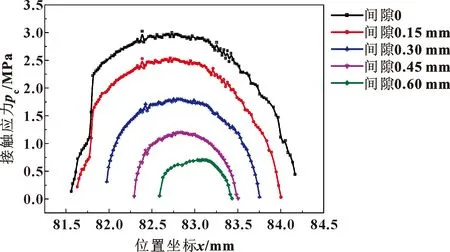
圖15 最大接觸壓力為最小時接觸壓力分布與間隙關系Fig.15 Relationship between contact pressure distributionand clearance when the maximum contactpressure is the minimum

從圖14和15還可看出，隨著間隙的不斷增大，最大接觸壓力不斷降低，接觸寬度也在不斷減小，泄漏發生的概率逐漸增強。因此，文中通過取不同間隙下的接觸壓力來計算泄漏率，從而驗證系統的可靠性。文中運用柵格滲漏模型及平行平板公式進行泄漏率求解。史建成[16]在PRESSON和YANG[17]建立的柵格滲漏模型基礎上來實現泄漏通道的尋找，文中基于文獻[16]的思路，通過將接觸壓力代入STANLEY模型[18]來計算出給定形貌變形后的接觸矩陣及通道高度，將接觸矩陣代入柵格滲漏模型來生成泄漏通道，最后基于平行平板公式計算出泄漏通道中的泄漏率。平行平板的泄漏率公式為

(2)

式中：Qv為體積流量；dx為泄漏通道的單位寬度(總長為O形圈周長)；h0表示截面泄漏通道形狀為三角形的高度；hi(i=1、2)表示泄漏通道的截面形狀為梯形的高度；μ為流體的動力學黏度，此處取值5.434 6×10-3Pa·s；dy為泄漏通道的單位長度(總長為接觸寬度)；Δp為密封面兩端的壓差，取值0.3 MPa。

圖16所示為間隙與泄漏率的關系。隨著擋板與溝槽之間間隙的不斷增大，泄漏率都呈現逐漸增大的趨勢。而隨著間隙進一步增大，最大接觸應力最小時的組合(記為最劣情況組合)的泄漏率明顯要高于標準尺寸組合。產生這種現象的原因是在該組合下橡膠密封圈直徑相對減小和溝槽深度相對增加，使得密封接觸區域及密封接觸壓力都較標準組合減小，從而引起泄漏量的增大。

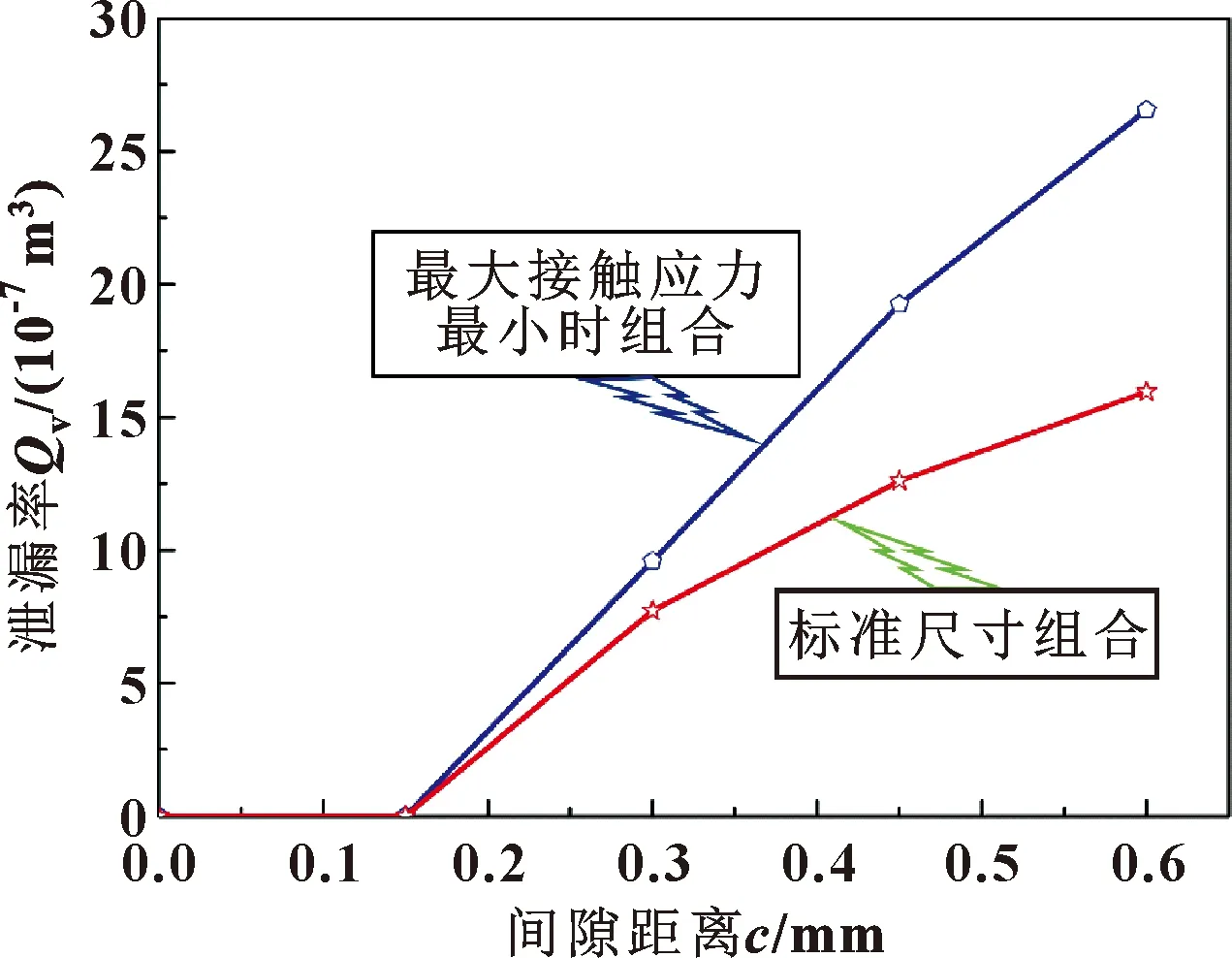
圖16 不同尺寸組合的密封的間隙與泄漏率關系Fig.16 Relationship between clearance and leakagerate of seals with different size combinations

3 結論

利用ABAQUS軟件對存有尺寸偏差的密封結構進行有限元仿真分析,探究結構尺寸偏差對結構組合密封性能的影響。具體結論如下：

(1)通過控制變量法獲得不同尺寸偏差下橡膠O形圈的接觸壓力分布、最大接觸應力的變化規律。結果表明：當溝槽不存在尺寸偏差時，增大O形圈的截面直徑或內徑，其密封端面的最大接觸應力呈增大趨勢；而當O形圈不存在尺寸偏差時，溝槽內徑的增加、底部倒圓角的增大以及溝槽深度的增大都會使得密封端面的最大接觸壓力呈現出增大的趨勢。

(2)通過對比不同尺寸偏差下的接觸壓力分布及最大接觸壓力的變化規律，推導出當密封結構的尺寸選取最大接觸壓力最小的組合時，隨著密封結構間隙的不斷增大，密封面泄漏率不斷增加，其密封性能相較于標準參數組合密封較差。

(3)在溝槽結構存有尺寸偏差的情況下，通過O形圈的合理選裝可以進一步提升密封性能。如當溝槽內徑偏小時，可選裝內徑為標準值而截面直徑較大的O形圈來增大其接觸寬度及接觸應力，進而保障部件的正常運行。