基于Flac3D驗證錨桿在層狀巖體中的優化錨固角度
楊 沖
(貴州省貴陽市烏當區水務管理局,貴陽 550025)
0 引 言
在自然界中,巖石體受到各種不同類型力的作用而保持穩定,歸結各種力的方向可將其分為豎直方向的力和沿水平方向的力。當巖石豎直方向和水平方向抗力小于外力作用時,巖石體就會發生破壞。為了保證工程建設過程中巖質邊坡的穩定性,采用錨桿進行錨固是現在最為普遍的工程措施。由于錨桿單價較高,因此如何降低成本成為行業研究的重點[1-6],其中通過合理設置錨桿錨固角度是有效提高錨桿使用效率、降低成本的一種重要措施。隨著科學的發展,采用數值模擬軟件對類似工程問題進行研究是現代科研的重要手段。唐云波[7]等采用Flac3D對預應力錨索抗滑樁的錨固角度進行了優化研究,得到了最優錨固角度。楊沖[8]針對邊坡中錨桿傾角對層狀巖質邊坡的錨固效率的影響采用Flac3D進行了研究,得到了錨桿在邊坡中不同位置受力情況不同應采取不同錨固方式的結論。本文在前人研究基礎上,采用數值模擬軟件Flac3D,對力學推導所得錨桿優化錨固角度進行驗證。
1 錨固角度確定
錨桿傾角會直接影響巖石體中錨桿的空間存在形式,進而影響錨桿對巖石體E3和E1的貢獻程度。由于現實工程建設中,絕大部分巖石體具有層理面,因此要保證加錨后巖石體抗壓抗拉強度達到最優值,必須考慮巖層面對錨桿的影響,見圖1。
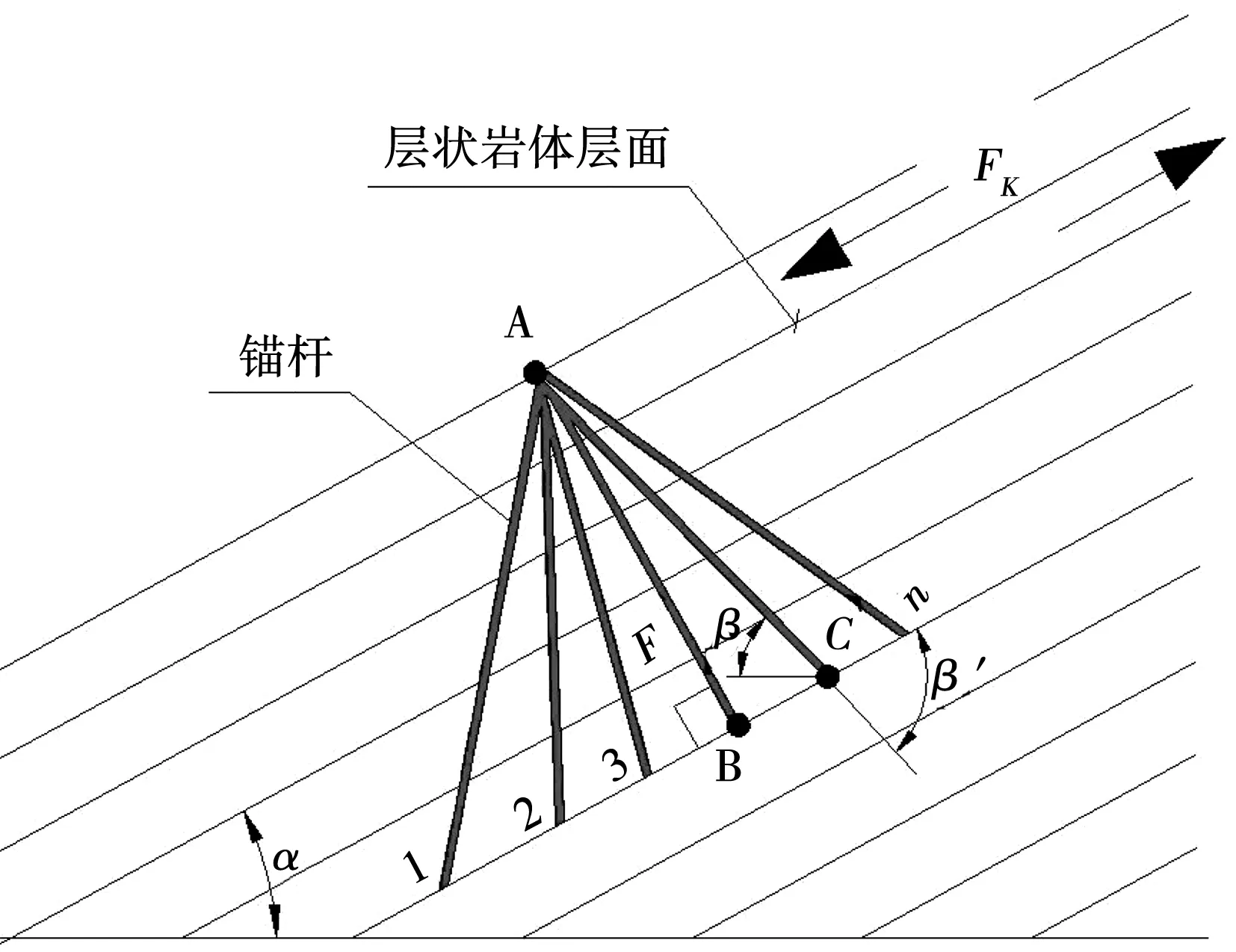
圖1 含層理面單元巖石體錨桿錨固示意圖
圖1表示在單元巖石體中錨桿以不同角度錨固含層理巖石體形式,巖石體層理面傾角為∠α。假設錨桿以A1、A2…An方式對巖石體進行錨固,任意選取錨桿AC進行研究,∠β為錨桿與層狀巖體巖層面水平方向的夾角(0°~90°)。假設任意錨桿AB與巖石體構成加錨巖體,當加錨巖石體受外力作用時錨桿可提供抵抗豎向、橫向以及巖石體沿層理面滑動的力,假設該力為F,則加錨巖石體中錨桿提供的抗滑力可表示為Fk:
FK=F(sinβ′tanφj+cosβ′)
(1)
根據圖1,有∠β′=∠α+∠β,根據三角函數關系可得到錨桿長度AC為:
(2)
假設單位長度上錨桿提供的抗滑力為q,通過三角形關系可以計算得到單q為:
(3)
將上式對于角β求偏導數,化簡得到:
(4)
由式(4)計算得出錨桿在含層理面巖石體中的最優錨固角度,可以看到錨桿錨固角度與巖石體層間內摩擦角和層狀巖體傾角有關。當巖石體層理面傾角特殊為0°時,式(4)可簡化為:
(5)
2 Flac3D數值模擬驗證
采用Flac3D數值模擬軟件建立含有水平層理面巖石體邊坡,即層理面傾角為0°,賦值該邊坡長寬高為40、5、80 m,坡角θ=45°,內摩擦角為0°,錨桿長度8 m,間距2 m,錨桿錨固角度從0°到90°間隔15°變化。
由于加錨巖石體可以看成一種正交各向異性模型,因此可采用Flac3D數值模擬軟件自帶的model orthotropic命令對該邊坡進行求解。通過計算,可以得到邊坡層理面傾角為0°時邊坡位移量隨錨固角度的變化值,見圖2。
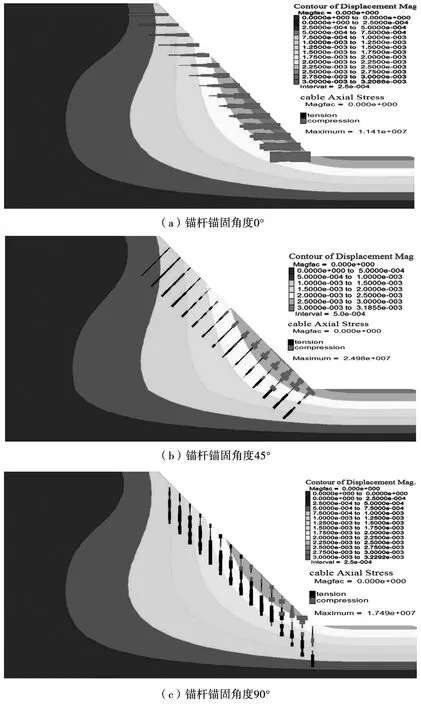
圖2 水平層理邊坡數值模擬代表位移云圖
3 數值模擬結果分析
根據Flac3D數值模擬軟件計算過程中生成的位移云圖可以看到,錨桿在巖石體中呈現出不同的受力情況。當錨桿傾角為0°時,錨桿基本呈紅色,此時錨桿受力方式主要為受壓;當錨桿傾角為90°時,錨桿基本為黑色,由此可以得到錨桿錨固角度從小到大變化過程中,錨桿受力方式為由壓到拉變化。還可以從云圖中看到,錨桿錨固角度不同時,邊坡位移量也各不同。將錨桿錨固角度與邊坡X方向和總位移量關系記錄繪制成表,見表1。
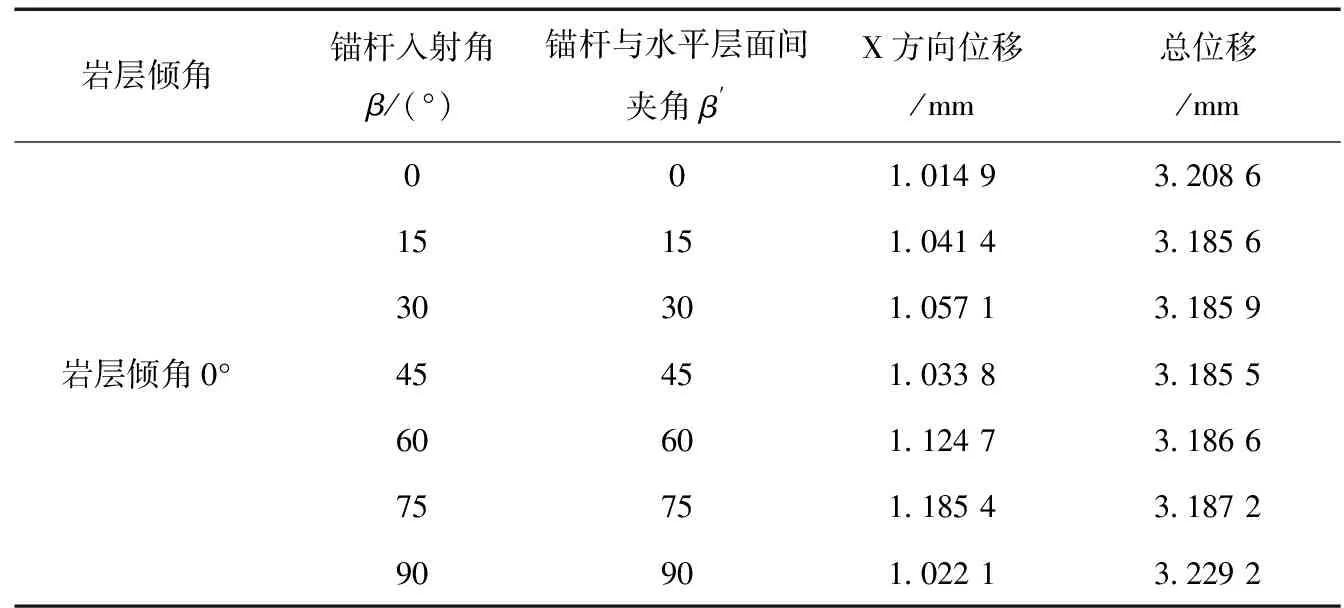
表1 水平層理面邊坡錨桿錨固角度與位移關系
根據表1中數據可以得到,水平層理邊坡中錨桿錨固角度為0°和90°時,邊坡總位移量較大,而X方向位移量較小。在15°到75°時,邊坡總位移量較小,而X方向位移量較大。特別地,當錨固角度為45°時,總位移最小,并且X方向位移量也相對較小。而邊坡位移量是影響邊坡穩定性的關鍵因素,會影響邊坡穩定性。本文探究內容為水平層理邊坡優化錨固角度,因此數值模擬中邊坡層理面傾角∠α=0。根據式(4)可得到水平層理邊坡優化錨固角度為45°,該結果與數值模擬得到結果一致,證明該計算式正確。
4 結 論
根據加錨巖石體力學分析以及Flac3D數值模擬計算結果,可以得到以下結論:
1)在含層理面巖石體邊坡中,錨桿的錨固角度不同錨桿受力方式也不同,錨桿錨固角度會直接影響加錨巖體邊坡的位移量,進而影響邊坡穩定性。
2)在水平層理面巖石體邊坡中,錨桿錨固角度從小到大變化時,錨桿受力方式為由壓到拉變化。
3)一般情況下,邊坡加錨角度取值計算公式為45°+φj/2-α。但當邊坡層理面傾角特殊為水平層理即0°時,錨桿的錨固角度只受內摩擦角影響,可簡化為45°+φj/2。

