基于泊松方程的空間波數混合域二度體磁異常數值模擬

趙東東，王旭龍，周印明，戴世坤

1.中國地質調查局南京地質調查中心，南京 210016 2.中南大學地球科學與信息物理學院，長沙 410083 3.有色金屬成礦預測與地質環境監測教育部重點實驗室(中南大學)，長沙 410083 4.湖南科技大學信息與電氣工程學院，湖南 湘潭 411201

0 引言

磁法勘探是地球物理勘探中發展比較成熟的方法之一，已經廣泛應用于直接尋找磁鐵礦及其共生礦床、固體礦產、石油天然氣構造的普查和不同比例尺的地質填圖以及深部、區域、全球構造的研究等[1-3]。在實際野外生產中，通常將走向方向尺度遠比垂直走向方向尺度大的地質體近似用沿走向無限延伸的二度體代替。

目前，磁異常數值模擬方法一般主要分為空間域方法和頻率域方法。空間域方法通過異常場解析式直接求取空間任意點的精確異常場，其優點是原理簡單、結果精確，缺點是解析式比較復雜，推導過程繁瑣，且當計算大量位置點異常場數據時，速度較慢。有關二度體的磁異常數值模擬研究最早就是在空間域開始的，Talwani等[4]首次給出了多邊形截面二度體磁異常解析表達式；在此基礎上，Talwani[5]在計算機上實現了近似二維棱柱狀多邊形數值模擬；Won等[6]根據泊松關系導出了多邊形截面二度體磁異常的解析式，并利用Fortran77實現了相關算法，優勢在于可以模擬地下任意觀測點的磁場；Shuey等[7]、Rasmussen等[8]以及Cady[9]在前人研究基礎上對原來的算法進行校正，使其能模擬實際地質體所產生的磁異常；賈真[10]系統地推導了均勻多邊形截面二度體磁異常及磁異常梯度正演計算公式，并重點探討了正演公式中所包含的奇異性；Jeshvaghani等[11]采用自適應有限單元法實現了基于拉普拉斯方程的二度體磁異常正演；Kravchinsky等[12]在Talwani[5]解析公式的基礎上編寫了一套基于Matlab的二度體磁異常模擬軟件，并提高了數值精度。

頻率域方法根據場源產生異常場的傅里葉變換解析表達式，通過數值方法計算該異常頻譜的反傅里葉變換得到異常場。相對于空間域方法而言，其優點是表達式簡潔，計算效率較高。在頻率域，Bhattacharyya等[13]推導了任意二度體的磁場頻率域表達式，并進行了反演研究；Pedersen[14]給出了任意二度體、二度半體(以三角形組合為其表面的模型)重磁異常頻率域表達式，并指出該公式相對空間域解析公式更為簡潔；吳宣志[15]將任意二維物體磁場的波譜解析表達式推廣至可用于任意變磁化強度模型；柴玉璞[16]將偏移抽樣方法發展為一整套完整的理論體系，有效提升了傅里葉變換的數值精度，使得頻率域方法逐漸在處理復雜模型正演問題中得以廣泛應用；吳樂園[17]在偏移抽樣理論的基礎上提出Gauss-FFT(fast Fourier transform)理論方法技術，有效提升了變換精度，降低了水平方向邊界條件帶來的影響，并將其應用于頻率域二度體磁異常正演，取得了不錯的效果。

然而，由于在面向實際應用的大規模、高效、高精度、精細化三維反演成像中，網格單元剖分數目達數千萬甚至數億，導致計算量和存儲量巨大，使得常規從積分方程的空間域和頻率域很難高效、精細模擬任意復雜模型；故在介于空間域和頻率域之間的空間波數混合域，從微分方程角度出發提出一種可將三維或二維問題分解為多個一維小問題的數值求解方法。該方法已成功應用于二度體重力異常和三度體位場正演模擬[18-19]，并且在計算精度和效率方面表現出一定的優勢。在此基礎上，本文將基于泊松方程的空間波數混合域方法[18]用于磁異常二維數值模擬。該方法通過一維傅里葉變換把二維磁位問題轉化為多個一維問題，由此大大減少了計算量，不同波數之間常微分方程相互獨立，具有高度并行性；保留垂向為空間域，有利于適應復雜地形的模擬，兼顧了計算精度與計算效率；采用有限單元法求解不同波數滿足的常微分方程，充分利用追趕法求解對角線性方程組的高效性以進一步提高計算效率[20]。在模型算例中，分別設計突變介質模型、連續介質模型和復雜地形模型用于驗證空間波數混合域二度體磁異常正演數值模擬方法的計算精度與計算效率。

1 基本理論

1.1 控制方程

弱磁性體滿足的二維泊松方程[21]為(詳見附錄A)

?2U(x,z)=?·M(x,z)。

(1)

式中：U(x,z)為磁位；M(x,z)為磁化強度矢量。對式(1)沿x方向做一維傅里葉變換，則有

(2)

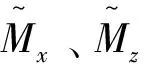
1.2 邊界條件

在無磁源區域，空間波數混合域磁位滿足的常微分方程(式(2))通解為

(3)

式中，A和B為通解的系數，表示任意常數。規定垂向坐標軸向下為正，上邊界z=zmin，下邊界z=zmax，如圖1所示。則上、下邊界條件為：

(4)

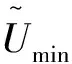
1.3 磁場和磁梯度張量計算

空間域磁感應強度、磁梯度張量與磁位的關系如下：

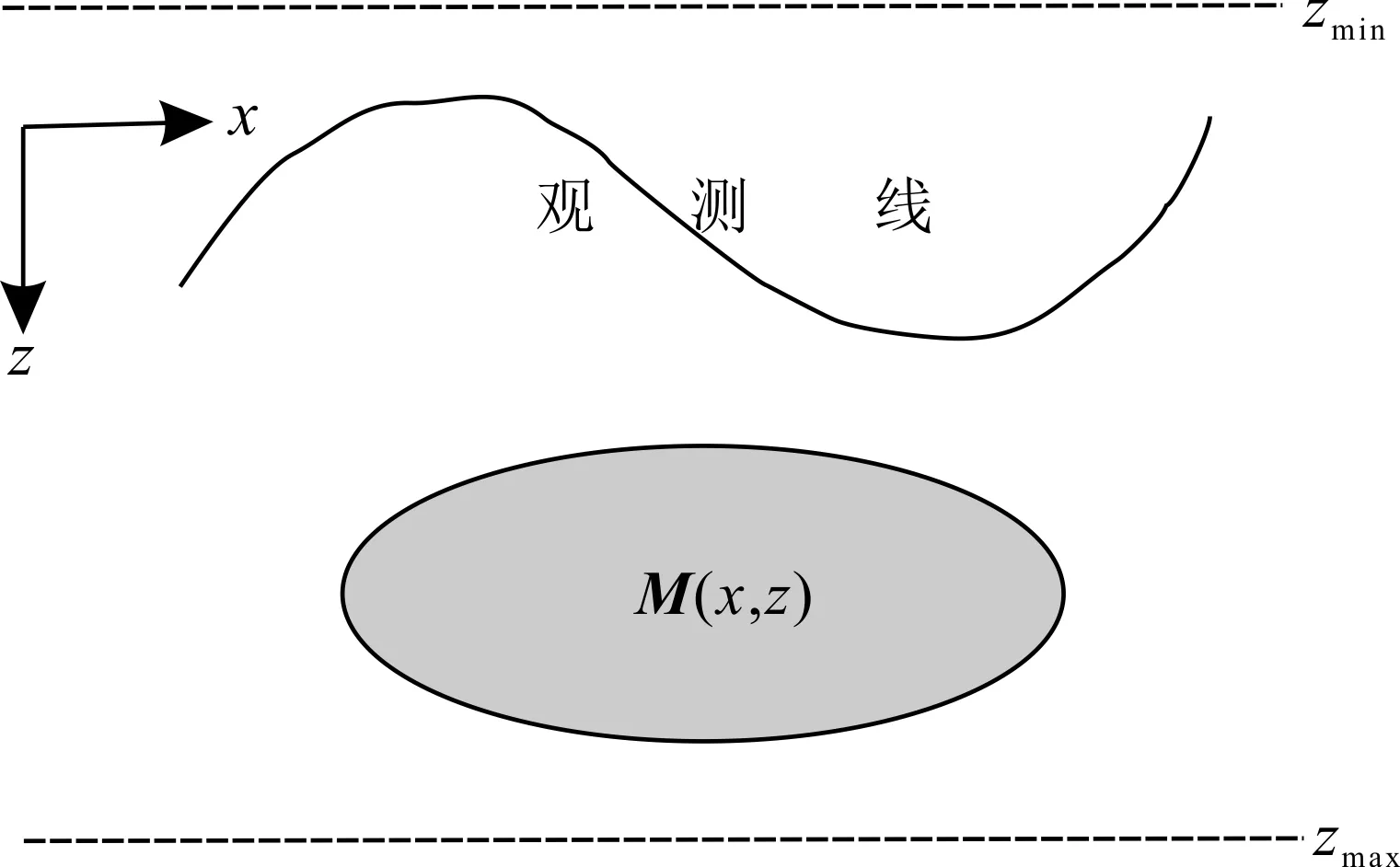
圖1 邊界條件示意圖

(5)

(6)

式中：B為空間域磁感應強度；T為空間域磁梯度張量。對式(5)和式(6)進行一維傅里葉變換可以得到：

(7)

(8)

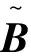
1.4 零波數處理

特別地，當k=0時，空間波數混合域磁位滿足的常微分方程為

(9)

式(9)相當于水平層狀磁性介質產生的磁場，即空間波數混合域的水平磁場為零，垂直磁場為磁化強度的垂直分量，具體形式如下：

(10)

(11)

(12)

2 常微分方程求解

式(2)與引力位滿足的空間波數混合域常微分方程類似[8]，本文采用基于二次插值的一維有限單元法進行數值模擬。該方法一方面能實現復雜模型和復雜地形的磁異常高精度模擬，另一方面利用追趕法求解有限單元法形成的對角線性方程組(五對角)具有計算速度快、占用內存小的特征。

聯立式(2)和式(4)，即是空間波數混合域二度體磁位滿足的一維邊值問題。基于變分原理構造泛函[20]，可得到與邊值問題等價的變分問題(詳見附錄B)：

(13)

(14)

其中：

和列陣Xe、Ze詳見附錄C。由于δuT≠0，故

Ku=P。

(15)

對于該五對角定帶寬線性方程組，采用追趕法實現高效、高精度求解，通過磁場、磁梯度張量與磁位之間的關系(式(7)和式(8))易得到空間波數混合域的磁場和磁梯度張量，采用Gauss-FFT對空間波數混合域磁位、磁場及磁梯度張量進行反變換，得到空間域的磁位、磁場和磁梯度張量[17-18]。

3 數值試驗

設計截面為矩形的常磁化率和變磁化率二度體模型[21]，用于驗證本文算法的正確性和可靠性。常磁化率和變磁化率模型空間展布及模型剖分參數均一致(圖2)，模擬范圍：x方向為-500～500 m，z方向為0～500 m，網格剖分規模為201×101，水平網格和垂向網格間距均為5 m；異常體x方向延伸范圍為-100～100 m，z方向為150～300 m。本文算法均采用Fortran95語言編寫，模型算例均在配置為CPU-i7-4790、主頻為3.30 GHz、物理內存為32.00 GB的工作站上串行測試得到。

3.1 突變介質模型

圖2a所示的突變介質模型中異常體的磁化率為0.01；給定地球正常磁場強度為45 000 nT，磁傾角為45°，磁偏角為0°。通過對比本文算法結果與解析結果[18]驗證該算法的正確性和計算精度。圖3為突變介質模型磁位、磁場、磁梯度張量數值解和解析解以及地面節點的相對誤差。

從圖3可以看出：突變介質模型磁位、磁場和磁梯度張量的數值解與解析解吻合較好，磁位最大相對誤差絕對值僅為0.42%，磁場分量Bx和Bz最大相對誤差均絕對值為0.48%；磁梯度張量的最大相對誤差均絕對值為0.45%。磁位、磁場以及磁梯度張量的相對誤差絕對值均小于0.50%，僅在零值線附近相對誤差較大，驗證了本文算法的正確性和可靠性，且精度較高。

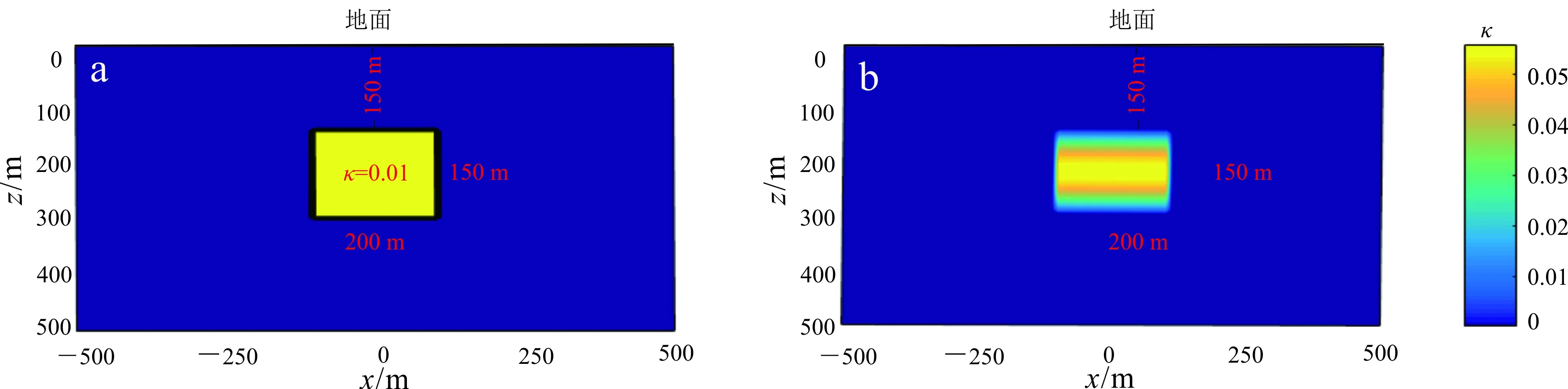
a. 突變介質模型；b. 連續介質模型。κ.磁化率。

3.2 連續介質模型

設計磁化率隨深度變化的連續介質模型(圖2b)，用于進一步驗證本文算法的適用性和可靠性。給定地球正常磁場強度為45 000 nT，磁傾角為90°，磁偏角為0°。異常體磁化率在深度方向上有二次變化規律：

κ=-(z-150)(z-300)×0.00001，
z∈[150,300]。

(16)

圖4為磁化率連續變化的二度體模型數值解與解析解及相對誤差。可以看出：連續介質模型磁位的數值解與解析解最大相對誤差絕對值為0.004%，磁場Bx的數值解與解析解最大相對誤差絕對值小于0.01%，與突變介質模型相比精度更高。這是由于連續介質模型在傅里葉變換過程中引入的誤差較小。

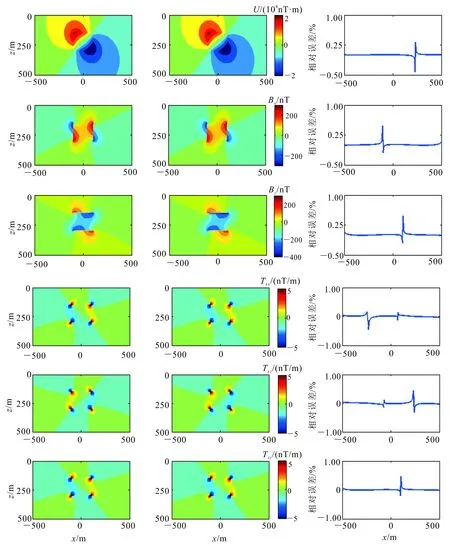
左.解析解；中.數值解；右.相對誤差。

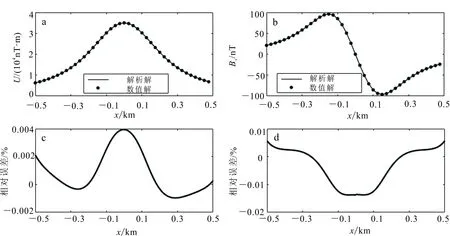
a. U數值解與解析解；b. Bx數值解與解析解；c. U相對誤差；d. Bx相對誤差。

3.3 計算效率

在任意復雜模型剖分滿足模擬精度的前提下，網格剖分規模越大，計算成本也越高；這是由于算法的計算效率主要由剖分網格規模決定的。圖5給出了不同網格剖分規模的模擬時間，可以看出：當網格

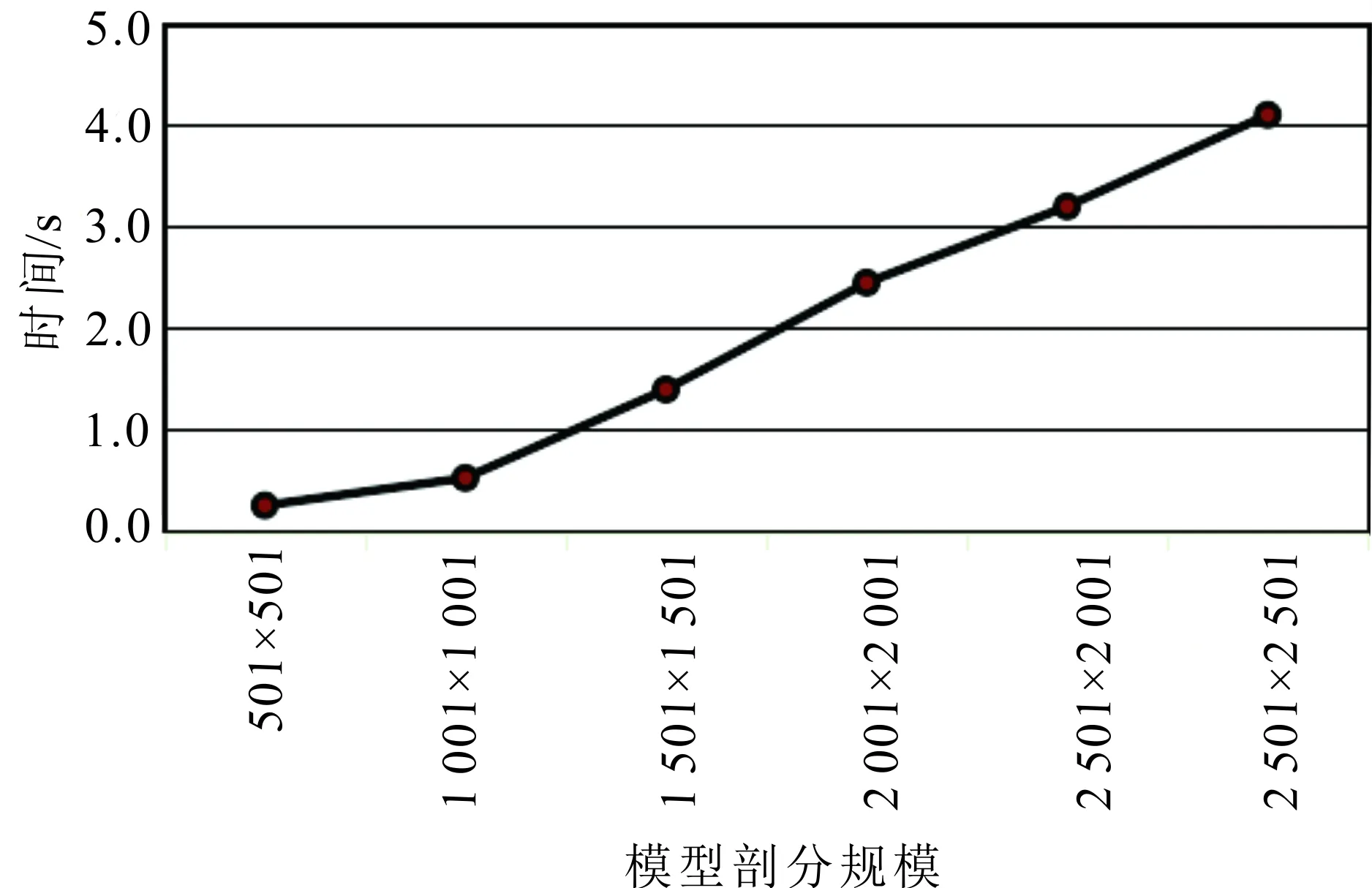
圖5 不同網格剖分規模的模擬時間

剖分為1 001×1 001時，模擬時間約為0.38 s，當網格剖分規模為2 501×2 501時，模擬時間為4.18 s；并且隨著網格剖分的指數增長，計算時間僅呈線性增長，而不是指數增長。可見本文算法不僅計算效率較高，而且網格剖分規模越大，計算效率優勢越明顯。

3.4 起伏地形模型

設計水平地形模型(圖6a)和起伏地形模型(圖6b)，用于進一步驗證本文算法在復雜起伏地形條件下的適用性和可靠性。模擬范圍：x方向為-250～250 m，z方向為-100～200 m，網格剖分規模為501×301。在水平地形模型(圖6a)中，異常體截面為矩形，沿x方向延伸范圍為-100～100 m，沿z方向延伸范圍為0～100 m；起伏地形模型(圖6b)由山谷和山脊構成，異常范圍與水平模型一致。異常體磁化率均為0.02，地球正常磁場強度為45 000 nT，磁傾角為45°，磁偏角為0°。利用本文算法計算觀測線高度為地面以上100 m的磁場及磁梯度張量，計算時間為0.21 s。

地面以上100 m高度的磁場及磁梯度張量模擬結果見圖7。可以看出：在山脊處，磁場Bz及磁梯度分量Tzz和Txz相對水平地形模型變化較快，正異常幅值增加，磁場Bx相對水平地形模型負異常幅值有所增加；在山谷處，磁場Bz和磁梯度分量Tzz和Txz相對水平地形模型變化減緩，但負異常幅值略有增強，磁場Bx相對水平地形模型變化明顯減緩，進一步驗證了本文算法在起伏地形條件下的適用性和可靠性。

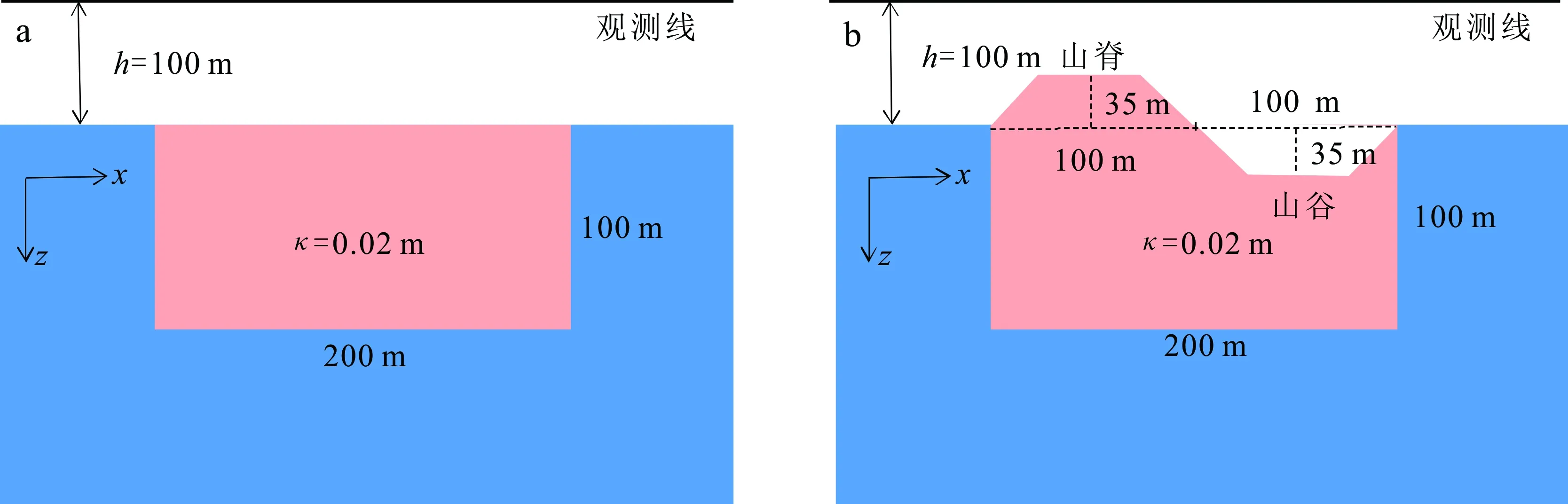
圖6 水平地形模型(a)和起伏地形模型(b)

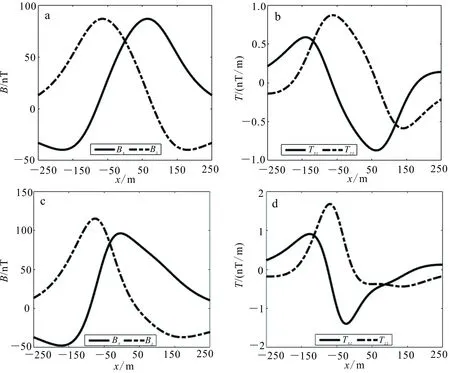
a. 水平地形磁場；b. 水平地形磁梯度；c. 起伏地形磁場；d. 起伏地形磁梯度。

4 結論

1)基于泊松方程的空間波數混合域數值模擬，主要利用了沿水平方向傅里葉變換方法和追趕法求解定帶寬線性方程組的獨特優勢，為二度體磁異常快速計算提供了一種新的研究思路和方案。

2)突變介質模型、連續介質模型和起伏地形模型的模擬結果表明本文算法數值模擬精度高、計算速度快，具有一定的實用價值。

3)該方法可能由于傅里葉變換的截斷效應或強制周期性在介質突變邊界引起較大的數值誤差，有待在下一步工作中繼續開展深入研究。

?×H=0；

(A1)

?·B=0。

(A2)

在高斯單位制(CGSM)中，B(Gs)和H(Gs)的關系為

B=H+M。

(A3)

式中：M是磁化強度，單位為emu，由感應磁化強度Ji和剩余磁化強度Jr組成。

M=Ji+Jr。

(A4)

且Ji與H成正比：

Ji=κH。

(A5)

式中，κ是磁化率。將式(A4)、式(A5)代入式(A3)可得

B=(1+κ)H+Jr=μH+Jr。

(A6)

式中，μ=1+κ是磁導率。將式(A6)代入式(A2)可得

?·[(1+κ)H+Jr]=0。

(A7)

由于H由正常磁場強度Ho和異常磁場強度Ha組成，即可表示為H=Ho+Ha，令

Ha=-?U。

(A8)

式中，U為磁位。將式(A8)代入式(A7)：

?·[(1+κ)?U]=?·Jr+?·[(1+κ)Ho]。

(A9)

又由于?·Ho=0，且在只考慮弱磁性體的條件下，將式(A9)移項化簡，有

?2U=?·(κHo+Jr)。

(A10)

式(A10)即為同時考慮感應磁化強度和剩余磁化強度的磁位基本方程。對于弱磁性體，式(A10)可以寫為

?2U=?·M。

(A11)

在實際磁法勘探中，一般采用CGSM單位制,而CGSM單位制中磁場強度以奧斯特(Oe)為單位，其分數單位是伽馬(γ)，1 γ=10-5Oe；在真空中μ=1，故B和H的量綱相同，它們的單位Gs與Oe大小相等，1 γ=10-5Oe=10-5Gs=10-9T=1 nT。

附錄B

針對邊值問題，構造一個泛函：

(B1)

其中：

(B2)

則其變分為

(B3)

將式(2)代入式(B3)可得

(B4)

將式(4)代入式(B4)得

(B5)

所以

(B6)

即空間波數混合域磁位的邊值問題與下列變分問題等價：

(B7)

附錄C

將整個區域的單元積分分解為各單元的積分之和，則

(C1)

令

(C2)

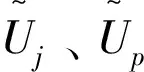
(C3)

式(C1)中第一項單元積分為

(C4)

其中，

(C5)

式中，l為單元長度。式(C1)中第二項單元積分為

(C6)

其中，

(C7)

式(C1)中第三項單元積分為

(C8)

利用形函數將jax、jaz表示為：

(C9)

其中：

(C10)

則式(C8)中第一個單元積分為

(C11)

其中，

(C12)

式(C8)中第2個單元積分為

(C13)

其中，

(C14)

式(C1)中，z=zmin、z=zmax分別為第一個和最后一個節點，可將其分別擴展成：

(C15)

其中，

(C16)

綜上，可將式(C1)表示為

(C17)