“模型”少一點 “積累”多一層

陳建洲 李玉榮 (江蘇省南京金陵中學河西分校 210019)

文[1]由一道幾何試題引發深度思考，給出了9個問題的解題分析，其中對問題1—3的求解引發了筆者的進一步思考：為何要那樣求解？有沒有更自然、適切的解法？深度思考的意義何在？在此與作者商榷.

問題1

如圖1，在矩形

ABCD

中，

CD

=3，

AD

=4，在

AD

邊上取點

E

，

H

，在

AC

上取點

F

，作正方形

EFGH

，連結

AG

，點

E

′是點

E

關于

AG

的對稱點，

AE

′交

BC

于點

P

，則

PC

的長為

.

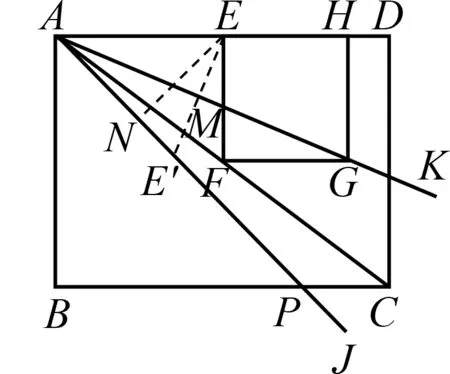
圖1

文[1]給出了此題的一個解答過程后指出：“解法利用點

E

與點

E

′相對稱的性質，得出

AK

平分∠

DAJ

，利用角平分線得出線段的比例關系，列出方程求解，但解題思路不容易想到，且角平分線的這個性質不在初中要求范圍之內，所列方程煩且難解.”接著作者在解答反思部分借助構圖探索出一個結論“若則并指出可以方便地求出一些與“二倍角”有關的問題.筆者不禁要問：這是從學生的角度思考問題嗎？此題怎么想到與二倍角有關聯呢？這個結論有實用的價值嗎？對教師而言，顯然沒有任何價值，因為他們熟悉公式對學生而言，或許記憶這個結論一時并不困難，但畢竟其適用的機會有限，所以真正遇到幾何問題，學生哪里會想到用這個結論？況且還不能直接用來求解問題(除填空題、選擇題).因此，筆者思考：此題有更自然、適切的求解方法嗎？分析 要求

PC

的長，只需求

BP

，既然

BP

的大小最終能確定，可推斷∠

APB

大小確定，而∠

APB

=∠

DAP

=2∠

DAG

，說明∠

DAG

大小確定，事實上，易知

解法1

如圖1，因為

EF

∥

CD

，所以△

AEF

∽△

ADC

，可得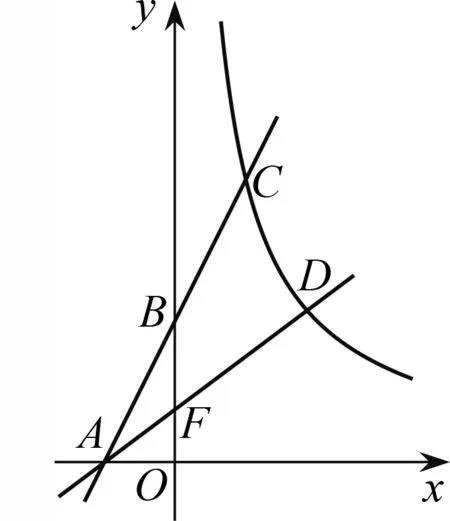

圖1

設

EF

=3

k

，則

HG

=

EH

=3

k

，

AE

=4

k

，所以

AH

=7

k

，可得連結

EE

′交

AG

于點

M

，作

EN

⊥

AP

于點

N

，則設

EM

=3

x

，則根據面積公式

EN

×

AE

′=

E

′

E

×

AM

，可得進而易證△

AEN

∽△

PAB

，可得即所以進而

解法2

同解法1得如圖2，延長

AG

,

BC

交于點

M.

因為

AD

∥

BM

，所以即因為

AB

=3，所以

BM

=7.

圖2

又∠

PAM

=∠

DAG

=∠

M

，所以

PA

=

PM

，設

PA

=

x

，則

BP

=7-

x.

在Rt△

ABP

中，根據勾股定理得3+(7-

x

)=

x

，解得所以進而

解法3

如圖3，同解法1得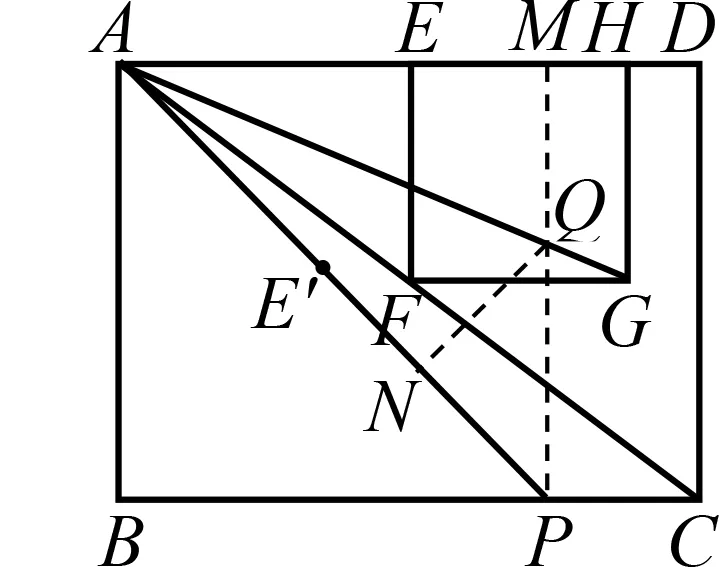

圖3

作

PM

⊥

AD

于點

M

，

PM

交

AG

于點

Q

，則

PM

=

AB

=3，

BP

設

QM

=3

k

，則

AM

=7

k

，

PQ

=3-3

k.

作

QN

⊥

AP

于點

Q

，則

AN

=

AM

=7

k

，

QN

=

QM

=3

k.

易證△

PNQ

∽△

PMA

，可得所以所以解得所以進而

解法4

如圖4，延長

GF

交

AB

于點

M

，交

AP

于點

N

，則∠

NAG

=∠

HAG

=∠

AGN

，所以

NA

=

NG.

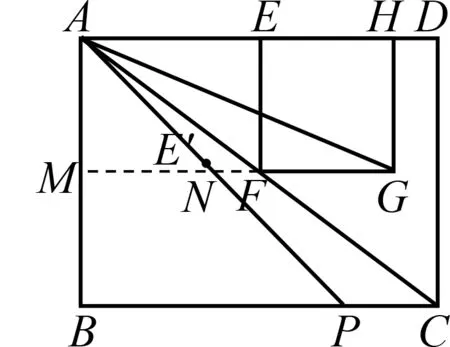
圖4

易證△

AMF

∽△

ABC

，可得設

AM

=3

k

，則

EF

=

FG

=3

k

，

MF

=4

k

，

MG

=7

k

，設

NG

=

x

，則

MN

=7

k

-

x.

在Rt△

AMN

中，根據勾股定理得(3

k

)+(7

k

-

x

)=

x

，解得即易證△

AMN

∽△

ABP

，可得即所以進而

評注 解法1—4添加的都是樸實的輔助線，構造出“角平分線+平行線=等腰三角形”等與角平分線有關聯的基本圖形，使用了面積法、勾股定理、相似三角形等基本計算工具，貼近學生思維發展區，解法自然、適切.

問題2

如圖5，正方形

ABCD

中，

AB

=6，

E

是

BC

邊中點，將△

ABE

沿

AE

對折，使得點

B

與點

F

重合，

AF

與對角線

BD

交于點

G

，求線段

GF

的長．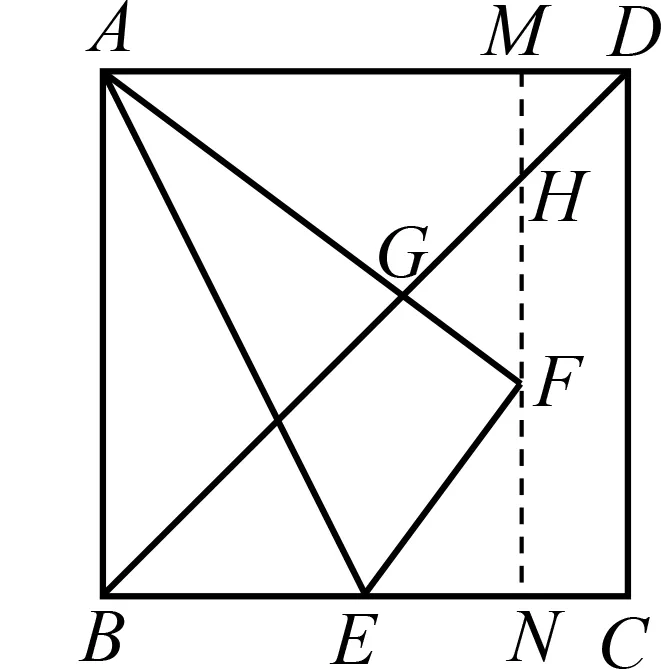

圖5

分析 此題文[1]是利用之前探究的結論求解的，筆者以為作為解答題顯然不妥.有更自然的求解方法嗎？要求線段

GF

的長，只需求線段

AG

的長，需借助△

AGB

或△

AGD

求解，但條件暫時不足．注意到∠

AFE

=90°，于是有兩個基本思路：一是構造“一線三等角型”相似三角形；二是構造“雙垂直共角型”相似三角形，最后借助“X型”相似三角形求解.

解法1

如圖5，過點

F

作

MN

⊥

AD

于點

M

，交

BC

于點

N

，則

MN

=

AB

=6，

AM

=

BN.

易證△

AMF

∽△

FNE

，可得設

EN

=

k

，則

MF

=2

k

，

FN

=6-2

k

，

AM

=

BN

=3+

k

，所以3+

k

=2(6-2

k

)，解得所以進而易證△

ABG

∽△

FHG

，可得所以

解法2

如圖6，延長

AF

,

BC

交于點

H.

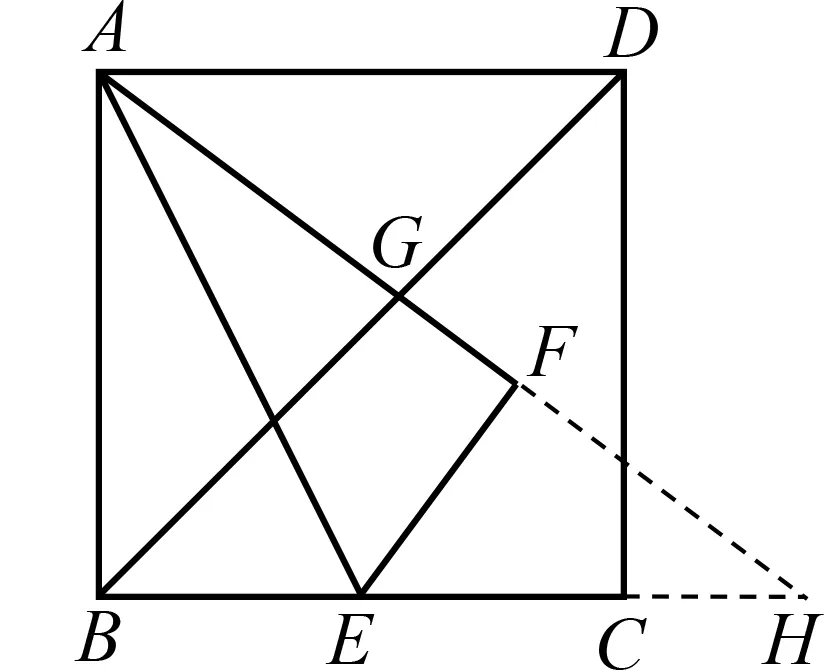
圖6

易證△

EHF

∽△

AHB

，可得設

FH

=

k

，則

BH

=2

k

，

EH

=2

k

-3，

AH

=6+

k

，所以6+

k

=2(2

k

-3)，解得

k

=4，所以

AH

=10，

BH

=8.易證△

ADG

∽△

HBG

，可得所以進而

解法3

如圖7，延長

AF

交

DC

于點

H

，連結

CF.

圖7

因為

EF

=

BE

=

EC

，所以∠

EFC

=∠

ECF

，可得∠

HFC

=∠

HCF

，所以

CH

=

FH.

設

FH

=

x

，則

AH

=6+

x

，

DH

=6-

x

，在Rt△

ADH

中，根據勾股定理得6+(6-

x

)=(6+

x

)，解得所以易證△

ABG

∽△

HDG

，可得所以進而

解法4

如圖8，延長

AE

,

DC

交于點

H

，延長

AF

交

DC

于點

M.

圖8

易證△

ABE

≌△

HCE

，可得

CH

=

AB

=6，

DH

=12，∠

BAE

=∠

EHC

=∠

HAM

，所以

AM

=

HM.

設

DM

=

x

，則

AM

=12-

x

，在Rt△

ADM

中，根據勾股定理得6+

x

=(12-

x

)，解得易證△

ABG

∽△

DMG

，可得所以進而

評注 筆者分別給出了問題1、問題2的4種解法，或許還有更多的解法可以探索，這不遠比套“公式”求解更能啟迪思維？

問題3

如圖9，在平面直角坐標系

xOy

中，直線

y

=2

x

+

b

經過點

A

(-1，0)，與

y

軸正半軸交于點

B

，與反比例函數交于點

C

，且

BC

=

AB

，點

D

是反比例函數上一點，連結

AD

，若則點

D

的橫坐標為

.

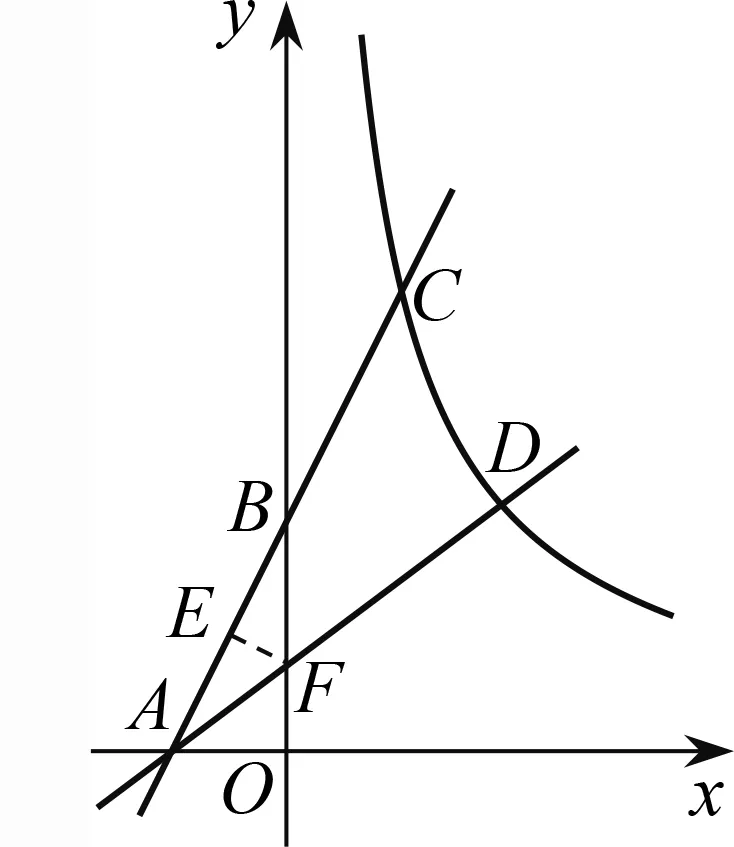
圖9

分析 文[1]刻意配制了問題2、3用以說明之前探究的結論的應用價值，但問題3的選取顯然不夠貼切，求解方法給人以“殺雞用牛刀”的感覺，由為何不用更自然的解法呢？

解法1

因為直線

y

=2

x

+

b

經過點

A

(-1，0)，所以如圖9，設直線

AD

交

y

軸于點

F

，過點

F

作

FE

⊥

AB

于點

E

，則設

EF

=

k

，則

AE

=2

k.

易證△

BEF

∽△

BOA

，可得故有

BE

=2

k

，從而解得所以進而可求出經過

A

，

F

的直線為易知

C

(1，4)，所以所以解得(舍去負根)，即

D

的橫坐標為

評注 這個解法看似繁瑣，但解法自然且具有一般性(如此時不存在二倍角，文[1]利用之前探究的結論算得無法 解決問題).當然，如果能結合已知條件從圖形中發現下面的解法更為簡潔.

解法2

如圖10，因為直線

y

=2

x

+

b

經過點

A

(-1，0)，所以

b

=2，

OA

=1，

OB

=2，進而所以

AF

=

BF

，設

AF

=

m

，則

OF

=2-

m.

在Rt△

AFO

中，根據勾股定理得1+(2-

m

)=

m

，解得進而以下同解法1.

評注 這個解法無需添加輔助線，更無需套什么“公式”或“模型”，獨具匠心.

不知從何時起，應對考試的“模型”充斥數學課堂教學，如“豬蹄”模型、“手拉手”模型、“12345”模型……讓人眼花繚亂，教學年歲較長的教師甚至聞所未聞、莫名其妙.《義務教育數學課程標準(2011年版)》明確指出：“課程內容的組織要重視過程，處理好過程與結果的關系.”基于此理念，曾經耳熟能詳的射影定理、相交弦定理、垂徑定理等重要定理在教材上都已刪去，那我們還有什么理由去編制所謂的模型(充其量也只能算基本圖形)讓學生去記憶、套用？解題是數學教師的最常見活動，學生學習數學更離不開解題，建立數學模型，對模型進行分析、求解，最終達到解決問題的目的無可厚非，甚至極為重要，但模型不能泛化，數學解題不能依賴并不常用的所謂“模型”或“結論”，更不宜在初中解題教學中大肆渲染一些遠離教材的“模型”甚至是超標的內容，美其名曰“拓展延伸”，實際上是加重了學生的學業負擔.泛化的模型等同于“拿來主義”：拿現成的“模型”去解難度大、思維含量高的數學題，表面上看解題過程簡化了，但失去的是更有價值的數學思維，實在得不償失.解題方法的教學理應遵循教材知識，執行課程標準，探尋貼近學生的發展區的自然解法，機械的“模型”或“結論”慎教、慎用，著力點應是強化過程性教學，讓學生更多地思考、探究，體驗獲取知識的樂趣，促進數學思維能力的提升，增效減負才能真正落到實處.

完稿之余，恰好看到廣東省2021年中考數學試卷第23題：

如圖11，邊長為1的正方形

ABCD

中，點

E

為

AD

的中點．連結

BE

，將△

ABE

沿

BE

折疊得到△

FBE

，

BF

交

AC

于點

G

，求

CG

的長．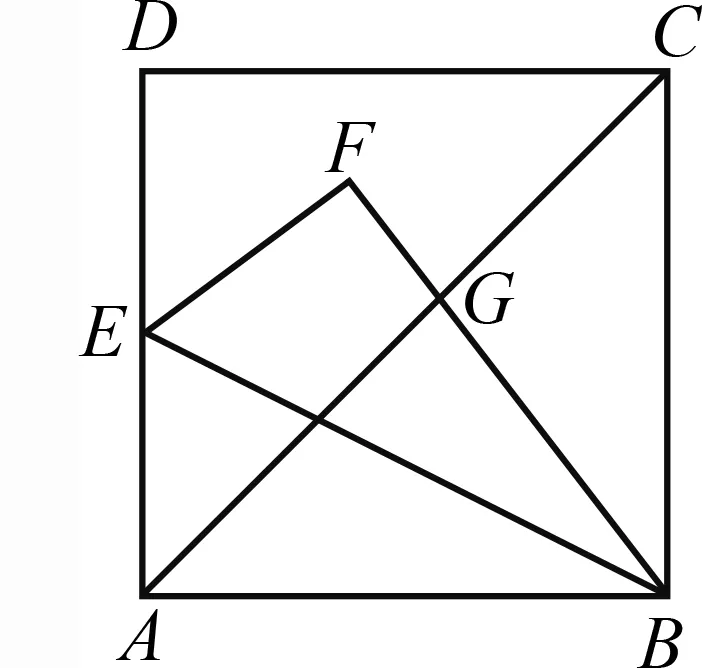

圖11

此題與問題2極為相似，考生該用什么樣的思路來求解呢？讀者自有分辨．