深度研析教材 優化學程設計
——“一元一次不等式(1)”的教學設計與感悟*
陸志強 (江蘇省南通市通州區平潮實驗初級中學 226361)
1 基本情況
1.1 授課對象
學生來自福建省廈門市海滄區教師進修學校附屬學校,其中大多為城市新市民子女,基礎一般,他們有一定的自學能力與運算能力,但缺乏數學學習的基本方法、策略的積累.
1.2 教材分析
教學內容為《義務教育教科書·數學》(人教版)七年級下冊第9章第2節“一元一次不等式”第1課時.在初中階段,不等式位于一次方程(組)之后,它是進一步探究現實世界數量關系的重要內容,它和一元一次方程無論是概念還是解法都有著一定的聯系.不等式的研究是從最簡單的一元一次不等式開始的,一元一次不等式及其相關概念是本章的基礎知識.解任何代數不等式(組)最終都是要化為解一元一次不等式,所以說,解一元一次不等式是一項基本技能.
教學中要引導學生利用已有的一元一次方程的概念及解法,體會兩者之間的異同,類比遷移,自主生成一元一次不等式的概念及解法,為進一步解一元一次不等式組作好充分準備.解一元一次不等式與解一元一次方程在本質上是相同的,即利用不等式的基本性質,逐步將不等式變形為x>a或x 教學目標 (1)經歷一元一次不等式概念及解法的探索過程,體驗、感受數學發現和創造的快樂,體會一元一次不等式和一元一次方程的聯系和區別;(2)在依據不等式的基本性質探究一元一次不等式的解法過程中,加深對化歸思想的體會;(3)了解一元一次不等式的概念,掌握一元一次不等式的解法. 教學重點引導學生通過自主探索和類比遷移,掌握一元一次不等式的解法. 教學難點創設情境引導學生自主確立一元一次不等式的解法步驟. 生1:一元一次方程. 問題2什么是一元一次方程? 生2:只含有一個未知數(元),并且未知數的次數都是1,等號兩邊均為整式,這樣的方程我們就叫做一元一次方程[2]. 設計意圖數學知識和方法內部具有邏輯一致性和連貫性,通過激活一元一次方程概念、明確概念的要點,為學生自主觀察發現一元一次不等式的概念奠定基礎. 問題3觀察下列不等式,它們有什么共同特征? 生3:這些不等式與一元一次方程類似:不等式兩邊均為整式,只含有一個未知數,并且未知數的次數是1. 師:像這樣,我們把只含有一個未知數、未知數的次數是1的不等式,叫做一元一次不等式.(揭示課題) 設計意圖引導學生從形式上觀察式子的共同特征,類比一元一次方程概念,概括出一元一次不等式的概念,同時還要厘清一元一次不等式概念的內涵,培養學生的觀察、歸納能力. 問題4下列不等式中,哪些是一元一次不等式?為什么? 生4:根據定義,(1)(2)都是一元一次不等式,而(3)(4)都不是一元一次不等式,(3)中未知數x在分母上,不是整式,(4)化簡后為x2-x<2x,未知數最高次數為2. 設計意圖為了加深學生對一元一次不等式概念的理解,設計有針對性的概念辨析題,從正反 兩個方面促進學生更深刻、更透徹地理解概念的本質. 問題5解一元一次方程的一般步驟有哪些?每步的依據是什么?分別有哪些注意事項? 學生交流后填表1. 表1 解一元一次方程的步驟 歸納:解一元一次方程本質上是將方程轉化為“x=a”的形式,是一個由繁化簡的過程. 設計意圖進一步解構解一元一次方程的步驟、依據、注意事項等知識,為順利遷移過渡到解一元一次不等式作充分準備. 例1解下列不等式,并歸納總結解一元一次不等式的一般步驟. 歸納解一元一次不等式的一般步驟、各步依據、注意事項,同步生成表2. 表2 解一元一次不等式的步驟 問題6解一元一次不等式與解一元一次方程的步驟、依據及注意事項有什么異同? 設計意圖對教材(學材)內容進行二度加工重構,由一道解不等式題目持續進行變式,目的在于喚醒學生的深度思考,在聯系和結構中自主地探索與發現,進一步體會化歸思想,增強學生思維的靈活性和敏捷性,優化思維品質. (囿于篇幅,以下過程略去) 教學過程是思想碰撞、智慧生成的過程.教材、教師、學生、教學環境等有機構成了整個課堂教學系統,是教學質量生成的基本要素.這些要素從不同的維度和不同的層面對教學活動、教學質量產生決定性和實質性的作用和影響[3].從根本上摒棄“一個定義、三項注意,緊接著‘鋪天蓋地’”的題海戰術,就要求我們從“教教材”轉為“用教材教”,最終朝向“用課標教”,基于課標、基于教材、基于學生,著力于學程的優化設計,合理開發適切的教學資源,為學生搭建合適的“腳手架”,引發學生深度思考. 既然教材的工具性地位無人撼動,就應充分發揮其工具性的價值,對教材深度解讀就是唯一有效的途徑. 一元一次不等式是在學習了一元一次方程和不等式及其基本性質的基礎上展開的.作為討論數量關系的又一數學工具,它與一元一次方程既有聯系又有區別.從式子特征上看,兩者都含有未知數,未知數的次數都是1,且兩邊都是整式,只是連接符號不同;解一元一次方程與解一元一次不等式都是通過適當的式子變形(去分母、去括號、移項、合并同類項、系數化為1)來獲得問題的解,都體現了化歸的思想.從方程到不等式,通過類比的方式接受新知識,充分發揮知識與方法的正向遷移作用,從而溫故知新、更上層樓. 正是因為教材承載著課堂教學的“應然”內容,它是有著自身內在結構的.我們在學程設計之初,切不可就事論事,務必要從系統和整體的視角來把握教材的基本結構,深度挖掘教材內容所蘊含的學科基本思想和方法,從更高的視角去審視教材.只有系統地研讀教材內容,厘清知識和方法的來龍去脈,才能依據課程目標和學生的學情確定教學的重難點;才能洞悉我們應該教什么、學生要學什么;才知道我們怎樣教、學生怎樣學、學到什么程度. 教材通過呈現不等式x-7>26的解集是x>33的形成過程,試圖說明解一元一次不等式過程中的“移項”與解一元一次方程中的“移項”是類似的,可以類比進行.進而利用不等式的性質,類比解一元一次方程的步驟,就可以求出一元一次不等式的解集.兩者均是化未知為已知,前者轉化為x>a或x “教材無非就是個例子.”作為“例子”的教材,我們要深入挖掘其中蘊含的知識、方法、文化、價值觀、評價等諸多內涵,多角度、多層面地解讀教材,吃透教材的精神與實質,重構對教材內容的認識和理解,才有可能提高教材內容的“附加值”[4].方程與不等式具有邏輯連貫性和一致性,只有讓學生真正地把將要學習的新內容與自己頭腦中的已有認知結構相聯系,才會產生積極的、有意義的學習,進而產生和完善新的認知結構.教師在分析教材時,還要轉換視角,站在學生的立場多角度分析、思考:學生已有了什么?還可以基于已有的經驗獲得什么?如何找到新舊知識的連接點?這樣才能真正地為學生的學習服務. 因此,創新解讀教材,關鍵要抓住內容的本質,要以獨特的視角去分析和研究教材內容,以新穎的方式去呈現與實施,努力尋找解決問題的最佳方式.促使學生形成強烈的創新意識與動機,讓他們帶著已有的知識與經驗走進課堂,在心靈的撞擊、成長的體驗、探索和追求中習得知識和方法,發展能力與素養,這才是我們創新使用教材的目的. 新課程改革給教師的教和學生的學帶來了新的挑戰,同時也給教師專業發展和學生的全面素養提升帶來新的機遇和發展空間.只有真正去理解教材、感悟教材、活用教材,依據課標、基于學情,為學生提供豐富而又適切的學習素材,加強學程活動的創新變構設計,才能讓學生真正親歷知識與方法的發現過程,引發學生的深度參與和思考,讓數學課堂煥發新的生命活力,數學課堂的精彩必將不斷延續.2 教學過程
2.1 激活經驗
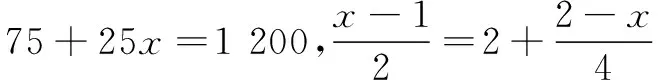
2.2 調用經驗
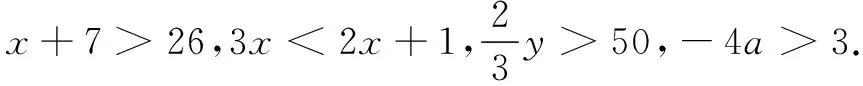
2.3 概念辨析
2.4 解構舊知

2.5 探索進階
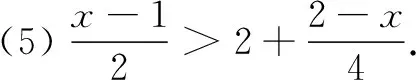
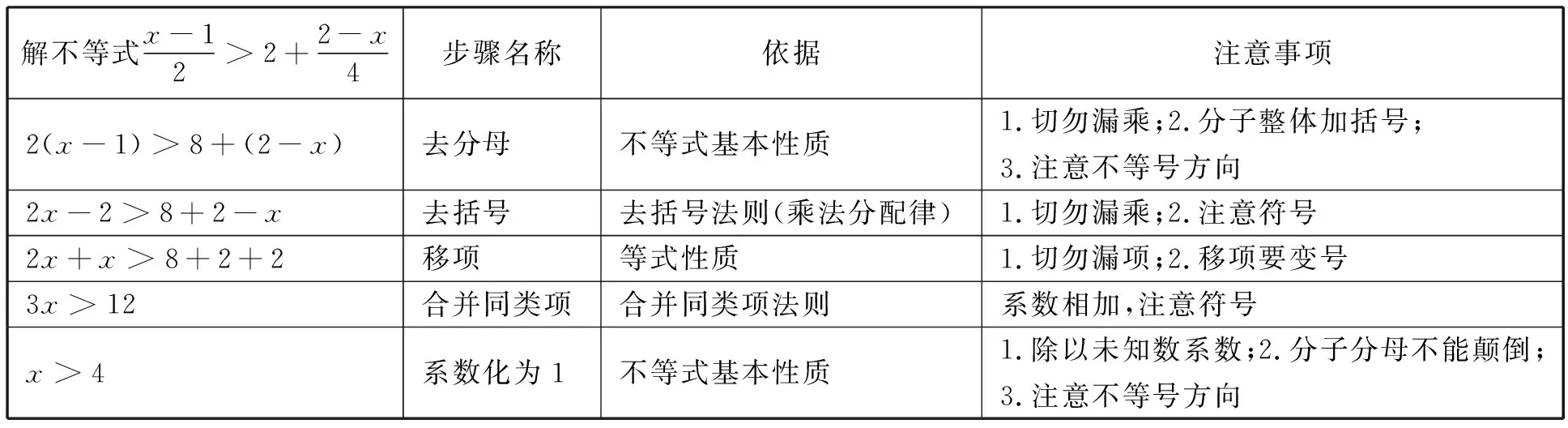
3 幾點感悟
3.1 系統解讀教材,在結構中教與學
3.2 多元解讀教材,在聯系中教與學
3.3 創新解讀教材,在發展中教與學
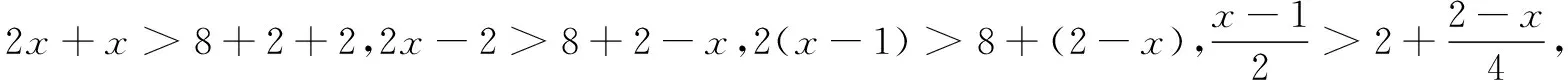
4 結語

