基于EEMD和小波閾值的短時交通流預測研究
馬瑩瑩,靳雪振
(華南理工大學 土木與交通學院,廣東 廣州 510640)
0 引 言
短時交通流預測可為交通控制及交通誘導提供數據支撐,是智能交通領域研究的重點和熱點。交通流數據采集過程中易受隨機因素影響,導致交通流數據非線性和不確定性增加,預測難度增大。短時交通預測領域現有研究大致可分為參數預測、非參數預測和組合預測等3大類。邱敦國等[1]綜合SARIMA模型在歷史周期性預測上的優勢和RBF模型在空間相關性的預測優勢,提出SARIMA-RBF模型,在同時考慮交通流歷史周期性和空間相關性情況下,其相較于單個模型具有更好的預測效果;李林超等[2]以交通流縱向時間及橫向空間相關性構建時間-空間狀態向量,采用網格搜索方法對支持向量回歸模型參數進行標定建立預測模型,結果表明,相對于傳統支持向量回歸模型,考慮交通流時、空間相關關系可提升模型預測精度。
深度學習算法[3]憑借其深層結構特點的優勢,開始被應用于短時交通流預測領域,其中包括堆疊自動編碼機(SAE)模型、深度置信網路(DBN)模型[4]、長短期記憶網絡(LSTM)模型[5]、卷積神經網絡(CNN)模型[6],其中以長短期記憶網絡的應用最為廣泛。翁小雄等[7]考慮引入交通流數據中的客車占比特征,提高了基于LSTM短時交通流預測模型的預測精度;閆佳慶等[8]通過對路網路段的時空分析, 并引入大型車因素,提高了基于GRU神經網絡的交通流速度預測模型的預測準確度。
交通流數據具有隨機性和非線性特征,傳統的小波分析通過對數據的分解與重構,能夠有效的對原始數據進行降噪,但小波去噪的效果會受小波函數的選取以及小波分解尺度大小的影響,從而影響組合預測模型精度。集合經驗模態分解(ensemble empirical mode decomposition ,EEMD)可依據數據自身的時間尺度特征進行分解,即將原始數據或信號分解為有限個本征模函數(Intrinsic Mode Function,IMF)。經分解得到的各IMF分量包含原數據不同時間尺度的局部特征信號,在使用時無需設定任何基函數,與建立在先驗性的諧波基函數和小波基函數上小波分析算法具有本質差別和特有優勢。
綜上,筆者提出一種基于EEMD和小波分析的數據分析方法,利用EEMD將原交通流時間序列分解為N個本征模態函數(IMF)和1個趨勢項(Res),并利用小波分析對IMF分量進行降噪處理。在此基礎上,提出兩類短時短時交通流預測模型構建方法,并分別構建基于長短時記憶網絡模型(long short-term memory, LSTM)、序列模型(Sequence to Sequence, Seq2seq)和引入注意力機制序列模型(sequence to sequence with attention,Seq2seq-Attention)的短時交通流預測模型進行對比,對所提兩類模型構建方法的有效性及普適性進行檢驗。
1 EEMD+小波分析組合算法
1.1 集合經驗模態分解
為解決經驗模態分解(empirical mode decomposition,EMD)在分解原數據時,模態混疊現象缺陷及迭代停止條件缺乏統一標準等問題,文獻[8]提出了集合經驗模態分解(EEMD),即通過一種噪聲輔助信號處理(NADA),利用添加均值為0的高斯白噪聲進行輔助分析,即EEMD,過程為:
Step 1:將白噪聲信號ω(t)加入原始信號x(t)中,得到信號x′(t):
x′(t)=x(t)+ω(t)
(1)
Step 2:將信號x′(t)進行分解,得到多個本征模態函數Ii(t)(i=1,2,…,N)和1個趨勢項r′(t):
(2)
Step 3:重復Step 1、Step 2,每次加入強度相同、序列不等的白噪聲:
(3)
Step 4:利用白噪聲頻譜的均值為零的特點,將所得IMF分量求均值,得到最終IMF分量Ii(t):
(4)
1.2 小波分析
對信號進行小波分解后,利用門限閾值對所分解的小波系數進行權重處理,然后對小信號再進行重構,即可達到信號降噪的目的。小波分析的基本思想是使用一簇小波函數來表示或逼近某一信號或函數,其中小波函數是小波分析的關鍵,是具有震蕩性、能夠迅速衰減到0的一類函數,即小波函數ψ(t)∈L2(R),且滿足:
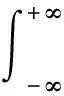
(5)
(6)
式中:ψ(t)為基小波函數,其可通過尺度的伸縮和時間軸上的平移構成一簇函數系;ψa,b(t)為子小波;a為尺度因子,反映小波的周期長度;b為平移因子,反映時間上的平移,且有a,b∈R,a≠0。
若ψa,b(t)是由式(6)給出的子小波,對于給定的能量有限信號f(t)=L2(R),其連續小波變換(continuous wavelet transform,CWT)為:
(7)
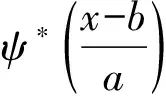
交通流時間序列數據屬于離散數據可表示為函數f(kΔ),其中:k表示樣本數量,且k=1,2,…,N;Δ表示取樣時間間隔,通常為5 min,則式(7)的離散小波變換形式為:
(8)
1.3 EEMD+小波分析組合降噪
EEMD分解得到的前幾個本征模態分量,通常集中了原信號中最顯著、最重要的信息,分量的頻率是從高到底排列的,并且會隨著信號的變化而變化。為充分利用EEMD與小波分析兩種算法在數據處理方面的各自優勢,筆者提出一種EEMD與小波分析組合的數據降噪方法,分為兩個步驟:
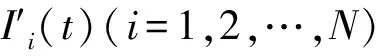
(9)
式中:N為分解所得IMF分量個數,其數量和IMF的定義有關,由極值點以及篩選終止條件來決定,也可在EMD分解中人為設置IMF分量的個數,使其不受終止條件的限制。
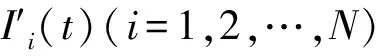
2 基于EEMD+小波分析算法的短時交通流預測模型
在運用EEMD+小波分析算法對數據進行預處理的基礎上,提出2類短時交通流組合預測模型構建方法:將經過EEMD+小波分析降噪的IMF分量和殘差分量進行重組,并將重組后的數據作為短時交通流預測模型的輸入數據,模型輸出值為最終預測結果(方法1);將經EEMD+小波分析降噪的IMF分量和趨勢項分別作為短時交通流預測模型的輸入數據,對模型輸出的各分量預測值進行重組,作為最終預測結果(方法2)。
2.1 方法1
將經過EEMD+小波分析算法降噪后的IMF分量和趨勢項進行重組,并將重組后的數據作為短時交通流預測模型的輸入數據,以此建立一個基于EEMD+小波分析算法,重構原時間序列數據的短時交通流預測模型,其主要實現步驟如下:
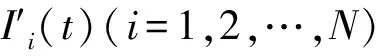
Step 2:將小波分析降噪處理后的本征模態函數I″i(t)和趨勢項進行重構,得到重構信號x″(t):
(10)
Step 3:選取Min-Max標準化方法對數據進行歸一化處理,即通過對原始數據的線性變換,使結果落到[0,1]區間;
Step 4:確定LSTM模型、Seq2seq模型、Seq2seq-Attention模型等3個短時交通流預測模型的網絡結構及超參數。模型超參數包括網絡層數、隱藏層單元數、學習率、迭代次數、激勵函數、損失函數、優化函數、批處理數量等;
Step 5:利用訓練集數據對建立的短時交通流預測模型進行訓練,更新各層連接權值,達到期望誤差或最大迭代次數后,停止訓練,反歸一化輸出結果得到最終預測值。
2.2 方法2
將經EEMD+小波分析降噪的IMF分量和趨勢項分別作為短時交通流預測模型的輸入數據,對模型輸出的各分量預測值進行重組,以此建立一個基于EEMD+小波分析算法分量預測組合的短時交通流預測模型,主要實現步驟如下:
Step 1:同方法1中Step 1;
Step 2:選取Min-Max標準化方法對IMF分量和趨勢項進行歸一化處理,即通過對原始數據的線性變換,使結果落到[0,1]區間;
Step 3:將經小波分析和歸一化處理后的I′i(t)和趨勢項分別作為單獨的數據集輸入建立的LSTM、Seq2seq、Seq2seq Attention等短時交通流預測模型;
Step 4:同方法1中Step 4;
Step 5:利用訓練數據對短時交通流預測模型進行訓練,更新各層連接權值,達到期望誤差或最大迭代次數后,停止訓練,反歸一化輸出結果。
Step 6:利用式(10)將模型輸出的各分量預測值進行重構,重構后的數據即為最終預測值。
2.3 評價指標
為對所建立的短時交通流預測模型的回歸效果進行分析,選取均方根誤差(RMSE)、平均絕對百分比誤差(MAPE)以及確定系數(R2)來評估模型擬合效果。其中RMSE衡量觀測值同真值之間的偏差;MAPE為0%表示完美模型,MAPE大于100%則表示劣質模型;R2也稱為擬合優度統計量,越接近1表明回歸線與各觀測點越接近,回歸的擬合程度就越好。計算公式如下:
(11)
(12)
式中:y′={y′1,y′2,…,y′n}為預測值,y={y1,y2,…,yn}為真實值。
3 實例分析
3.1 數據描述
研究數據來自加拿大Whitemud Drive高速公路,它是一條橫穿加拿大阿爾伯塔省埃德蒙頓市的市內高速公路,全長28 km,基本限速為80 km/h,數據記錄頻率為20 s/次,在主干道和閘道上裝有地感線圈,用于觀測車流量、車速以及車輛密度。
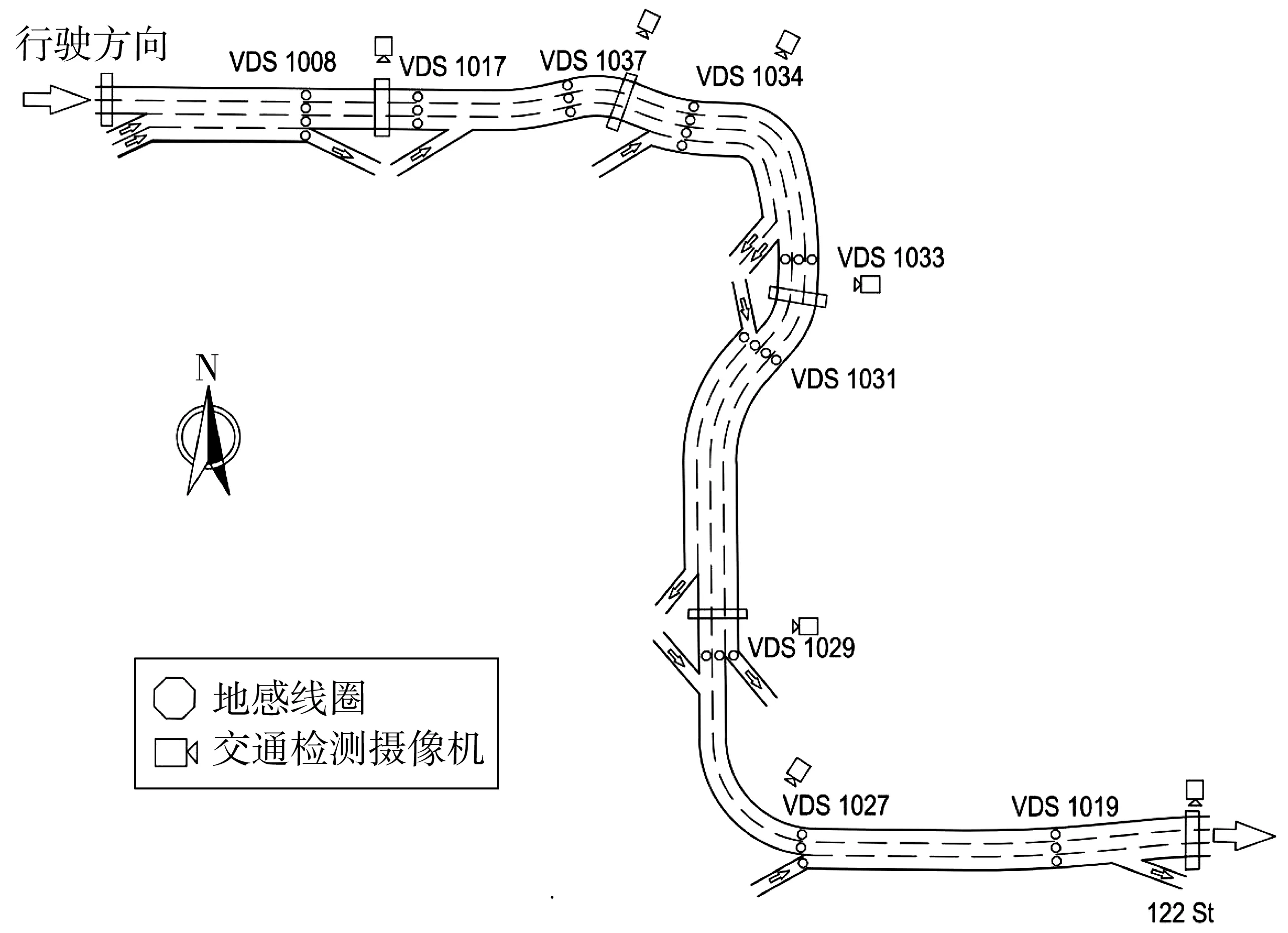
圖1 Whitemud Drive高速地感線圈位置分布Fig. 1 Position distribution of Whitemud Drive high-speed ground induction coil
選取該高速東行方向的地磁線圈數據作為研究對象,隨機選取VDS1017、VDS1034、VDS1029、VDS1019這 4個檢測器數據為研究對象,選取2015年8月8日至28日(剔除周末數據)共15天數據,以5 min時間間隔進行聚合,前14天數據作為模型訓練集(共4 032組),第15天數據作為模型測試集(共288組)。
3.2 EEMD+小波分析算法對原數據降噪
利用EEMD算法對VDS1017檢測器處流量數據進行分解。該信號經過EEMD分解得到10個本征模態分量和1個趨勢項Res,結果如圖2。
由于隨機噪聲信號在不同時刻的關聯性較弱,因而其自相關函數在零點處有最大取值,然后在零點兩旁迅速衰減接近于0;而一般信號的自相關函數在0點取得最大值后緩慢振蕩,不出現迅速衰減至0的現象。因此,對EEMD分解所得IMF分量進行自相關計算,利用含噪分量自相關函數在零點附近迅速衰減的特點來實現對含噪IMF分量的篩選。將EEMD分解得到的IMF分量進行歸一化自相關函數處理,結果如圖3。
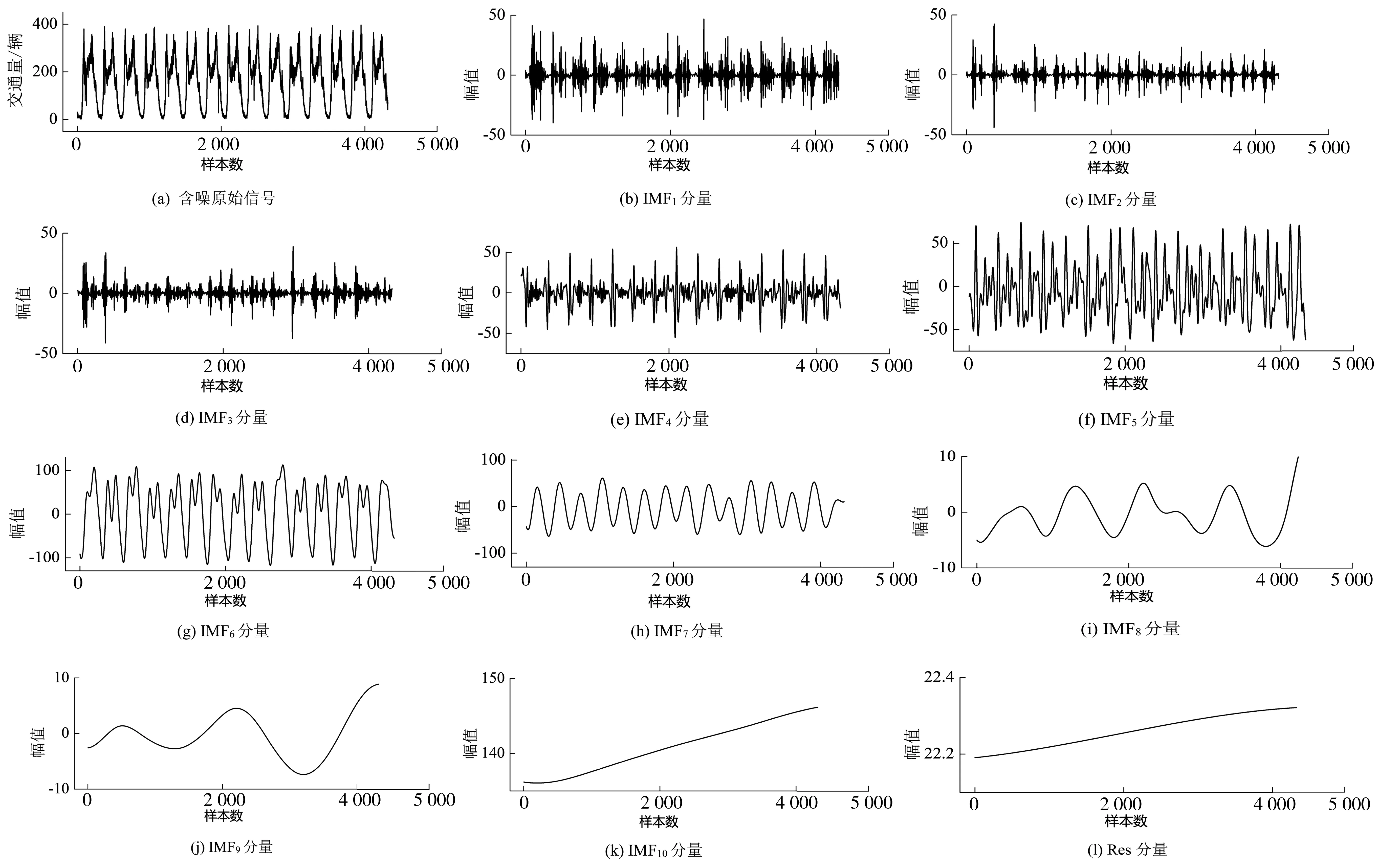
圖2 含噪原始信號的EEMD分解結果Fig. 2 EEMD decomposition results of noisy original signal
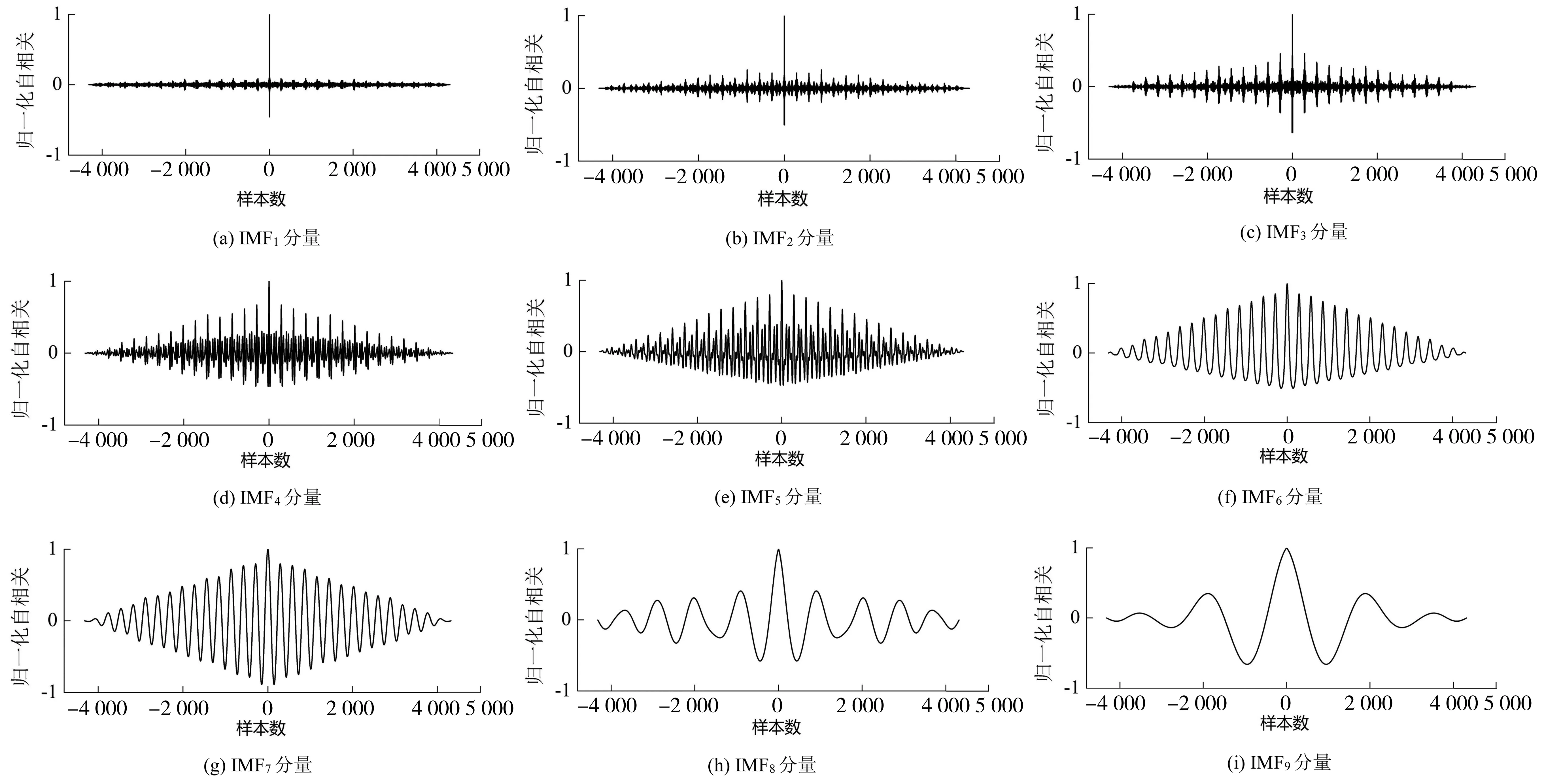

圖3 各階IMF分量的歸一化自相關函數Fig. 3 Normalized autocorrelation function of each order of IMF components
根據上述分量篩選原理,IMF1~IMF3在零點處取得最大值后,在零點兩旁迅速衰減,表明這3個分量具有明顯的含噪特征。因此,選取前3個IMF分量進行小波分析處理,其中小波基函數選取db4小波系,分解層數設定為3,同時保留其他信號主導的IMF分量與余項,小波去噪結果如圖4。
由圖4可知:經小波降噪處理后,IMF1~IMF3中包含的噪聲被有效濾除。
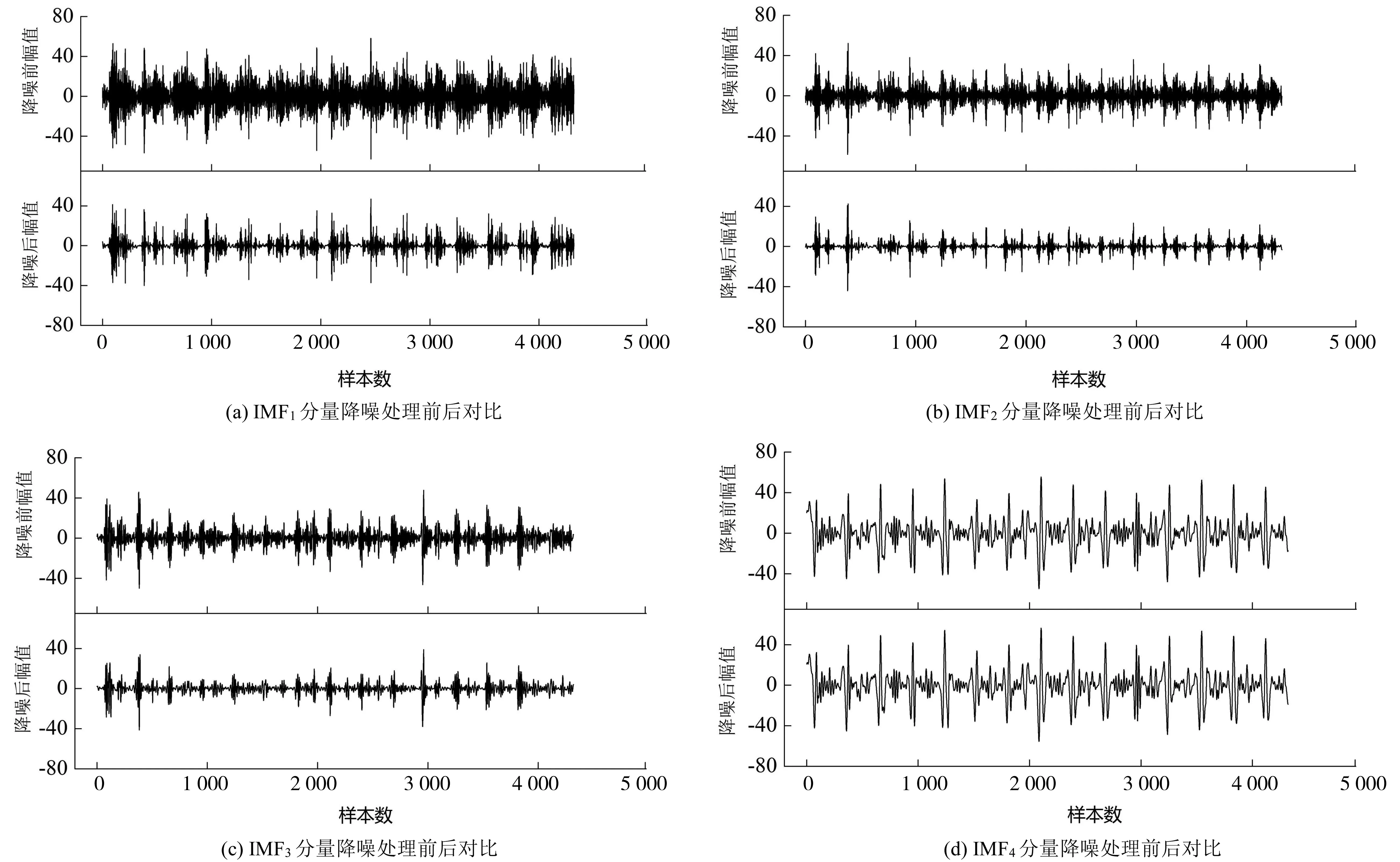
圖4 小波降噪效果分析Fig. 4 Analysis of wavelet noise reduction effect
為驗證篩選方法的有效性,對IMF4作小波分析處理,觀察圖像發現降噪后的IMF4與原IMF4分量幾乎無變化,可知IMF4分量中幾乎不含噪聲,進一步表明了篩選方法的有效性。
3.3 預測結果分析
運用VDS1017、VDS1034、VDS1029、VDS1019 這4個檢測器處數據,對基于方法1、方法2與LSTM模型、Seq2seq模型、Seq2Seq Attention模型組合構建的短時交通流預測模型的有效性和適應性進行分析,將所提方法1、方法2分別與單一的LSTM模型、Seq2seq模型、Seq2Seq-Attention模型和小波分析-LSTM模型、小波分析-Seq2seq模型和小波分析-Seq2Seq Attention模型的預測性能進行對比實驗,結果如圖5。
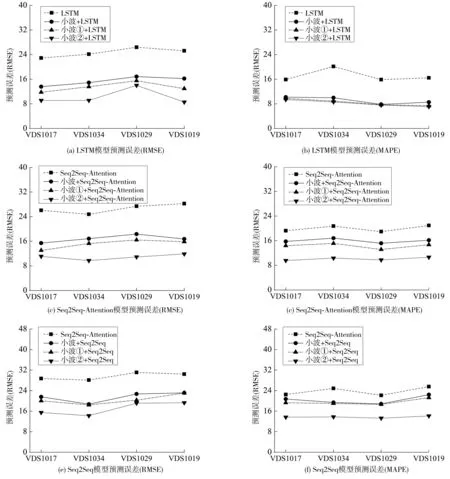
圖5 模型誤差指標對比Fig. 5 Comparison of model error indicators
對比選取的四個模型的均方根誤差、平均絕對百分比誤差可知:相較于單一的LSTM模型、Seq2seq模型、Seq2Seq-Attention模型和小波分析-LSTM模型、小波分析-Seq2seq模型和小波分析-Seq2Seq Attention模型,基于方法1、方法2與LSTM模型、Seq2seq模型、Seq2Seq-Attention模型組合構建的預測模型的誤差評價指標均明顯下降,模型性能最好的為基于方法2的組合預測模型、其次是基于方法1的預測模型,最后分別是基于小波分析的組合預測模型和單一模型。
筆者所提的兩類組合預測模型能大幅提高原預測模型的預測性能,方法2對于模型的提升效果最佳,并在LSTM模型、Seq2seq模型、Seq2Seq-Attention模型這3種類型的模型中均得到驗證。表明筆者所提出的兩類組合預測模型構建方法具有很高的準確度和普適性。
4 結 語
針對交通流數據非線性和不確定性的特點,利用集合經驗模態分解(EEMD)和小波分析來去除原交通流時間序列數據中的隨機噪聲部分,并在此基礎上提出的兩類短時交通流組合預測模型構建方法。通過借助長短期記憶網絡(LSTM)、序列模型(Seq2seq)、引入注意力機制序列模型(Seq2seq-Attention)等短時交通流預測模型進行試驗,表明所提兩類模型構建方法具有很高的有效性和普適性,通過分別與單一的LSTM、Seq2seq和Seq2Seq-Attention模型以及基于小波分析與LSTM、Seq2seq和Seq2Seq-Attention模型的組合預測模型進行對比實驗,表明兩類方法均能有效提升初始短時交通流預測模型的預測性能,且方法2對于模型的提升效果更加顯著。
筆者試驗場景為高速公路斷面,未充分考慮道路網絡的空間復雜性及其他維度信息,如速度、密度、占有率或天氣狀況等外部信息,后續研究將結合復雜的交通網絡及道路環境構建預測模型,增強預測模型的泛化能力,進一步提高短時交通流預測模型性能,為高速公路信息預測和交通誘導措施制定提供支撐。

