A FRACTIONAL CRITICAL PROBLEM WITH SHIFTING SUBCRITICAL PERTURBATION*

Qi LI (李奇)

College of Science，Wuhan University of Science and Technology，Wuhan 430065，China

E-mail:qili@mails.ccnu.edu.cn

Chang-Lin XIANG (向長林)?

Three Gorges Mathematical Research Center，China Three Gorges University，Yichang 443002，China

E-mail:changlin.xiang@ctgu.edu.cn

Abstract In this paper，we consider a class of fractional problem with subcritical perturbation on a bounded domain as follows: We prove the existence of nontrivial solutions uk of (Pk) for each k∈(0，∞).We also investigate the concentration behavior of the solutions uk as k→∞.

Key words Subcritical perturbation;nontrivial solutions;concentration

1 Introduction

Let Ω?RNbe a bounded smooth domain and let 0＜s＜1.In this paper，we consider the fractional problem

whereg(x) is a positive continuous function，and (-Δ)sis the fractional Laplace operator defined by

withP.V.being the principle value andCN，sa normalization constant (see，for instance，[3]and references therein for further details).Closely related to problem (Pk) is the following limit problem:

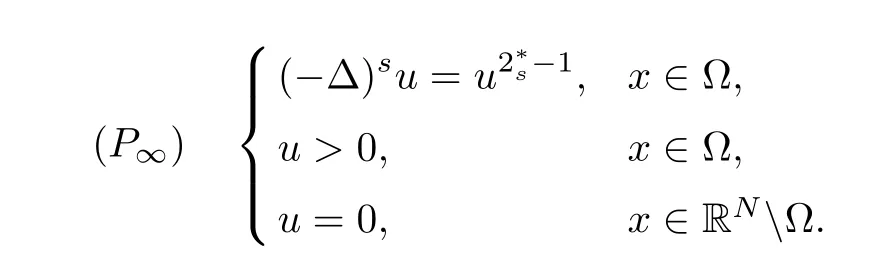
To make the notion of a solution to problem (Pk) clear，we introduce the function spaces

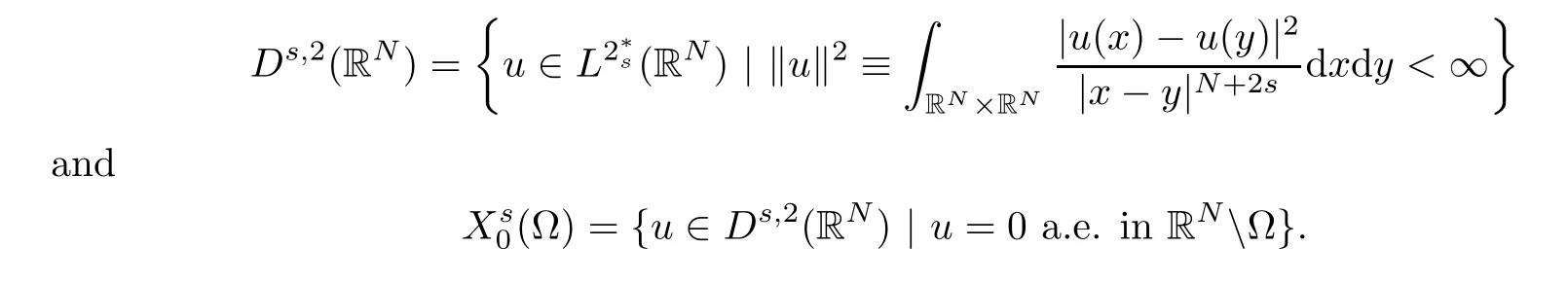
Then，a functionu∈X(Ω) is said to be a (weak) solution of problem (Pk) if

for anyφ∈X(Ω).

Recently，a great deal of attention has been devoted to fractional and non-local operators of elliptic type，on account of both of their interesting theoretical structure and applications;see，for example，[1，2，6，8，10，13，15–20]and references therein.It is well known that the existence of nontrivial solutions of (P∞) depends on the geometry of domains.In particular，if Ω is a star shaped domain，the Pohozaev identity (see[14]) implies that (P∞) admits no nontrivial solutions.Therefore，in order to find the nontrivial solutions of (P∞)，one can modify the geometry (see[12]) or perturb the critical term(see[9，11]).In this paper，our problem is motivated by the interesting work[4]of Gazzola，where the author studied the problem

with Δpu=div (|?u|p-2?u) being the usualp-Laplacian operator andThis problem can be seen as an interesting variant of thep-Laplacian version of the Brézis-Nirenberg problem

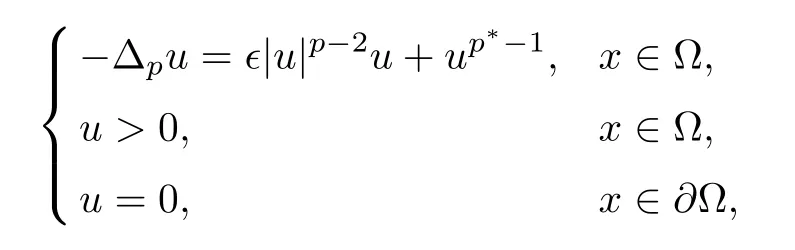
where the lower order perturbation∈|u|p-2uis replaced by the typeg(x)[(u-k)+]q-1，due to which a concentration phenomenon appears naturally as the parameterktends to infinity.Indeed，Gazzola obtained not only the existence of nontrivial solutions of，but also the concentration phenomena ask→∞.Motivated by[4]，we aim to extend the results of Gazzola[4]for non-local operator (-Δ)s.This，however，is not a trivial extension.The main difficulty is due to the non-local nature of the fractional Laplacian operator (-Δ)s.The analysis is far more difficult than that of the usual Laplacian.

In order to obtain nontrivial solutions of (Pk)，we define the energy functional of problem (Pk) for eachk∈(0，∞) as follows:

foru∈X(Ω).We also denote the energy functional of the limit problem (P∞) by

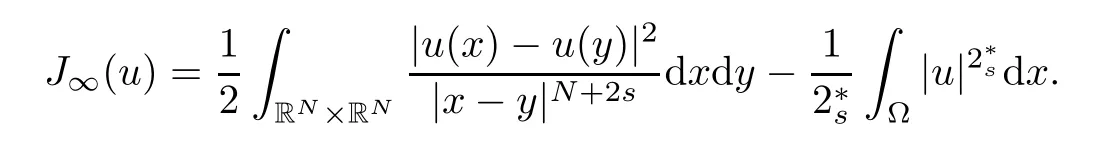
Then we turn to finding a critical point of the energy functionalJkfor eachk.Observe that the functionalJkhas a mountain pass geometry.This inspires us to apply the famous mountain pass lemma to derive solutions for problem (Pk).

It is well known that the embeddingis not compact.From[1]，we know that the best embedding constantSs，defined by

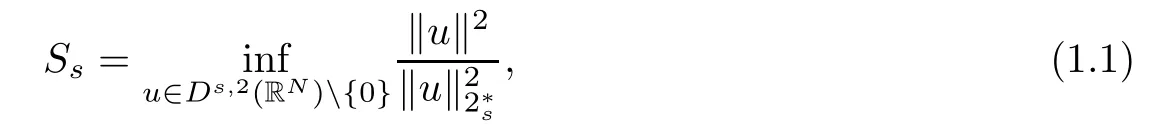
can be achieved，where ‖u‖pdenotes theLp-norm.Moreover，Ssis attained only by

for some constantsCN，s，μ＞0，andx0∈RN.Using the methods of[5]，we cut offthe above optimal function and get an estimate of the critical value.In order to get the estimate，we assume that

In addition，we assume that

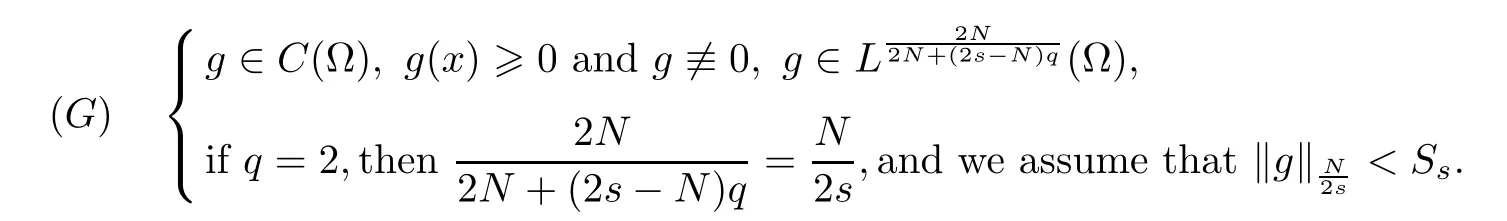
Since we are interested in positive solutions，we define the set of nonnegative functions

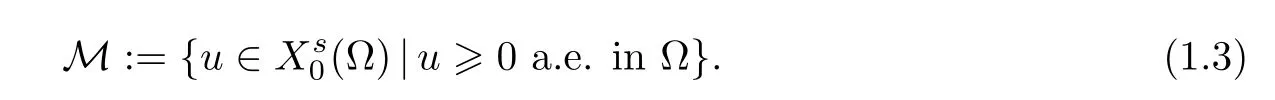
It is easy to check that the set N:={u∈M|J∞(u)＜0}is not empty.Takingv∈N，consider the class

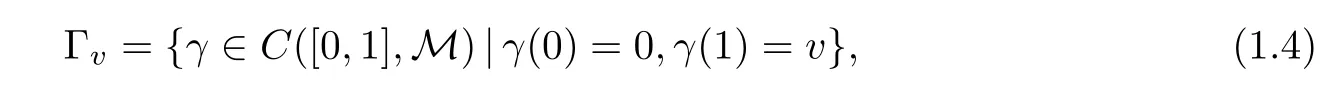
and denote the mountain pass value

Definition 1.1For eachk∈(0，∞]，we say that a solutionuk∈X(Ω) of (Pk) is a mountain pass solution at the energy levelckifJk(uk)=ck.

First we have a nonexistence result (see for example[14])，which can be stated as follows:

Theorem 1.2There are no mountain pass solutions of (P∞).

Second，we have an existence result for eachk，which can be stated as follows:

Theorem 1.3Assume (1.2) and (G).Then，for anyk∈(0，∞)，there exists a mountain pass solutionukof (Pk).Moreover，there existsΩ such that.Finally，if{km}?(0，∞) is a sequence such thatkm→k∈(0，∞) and{ukm}denote the mountain pass solutions of (Pkm)，then there exists a mountain pass solutionukof (Pk) such thatukm→ukin，up to a subsequence.

Theorem 1.3 will be derived by a careful estimate on the dependence of the critical valuesckwith respect tok;see Section 2 for details.We also investigate the behavior of mountain pass solutions as the parameterktends to infinity.The results read as follows:

Theorem 1.4Assume (1.2) and (G).Letukbe mountain pass solutions of (Pk) for eachk∈(0，∞).Ifk→∞，then

(i)uk?0 in.Moerover，there existx0∈and a subsequence{ukm}?{uk}such that (askm→∞):

Finally，ifdenote any of the points found in Theorem 1.3，then we haveaskm→∞.

From Theorem 1.3 we know that the set

is not empty.Moreover，using Theorem 1.4，we can see that Ω(uk) collapse to the single pointx0.The following result give us a more precise location ofx0:

Theorem 1.5Assume (1.2) and (G).Letukbe the mountain pass solutions of (Pk) for eachk∈(0，∞).Then，there exist.Moreover，ifx0andukmare as in Theorem 1.4，then for any such，we haveask→∞.In particular，x0∈Ωg.

We shall now prove some preliminary results in Section 2，and then we prove our main results in Section 3.Our notations are standard.We will useCto denote different positive constants from line to line.

2 Preliminary Results

In this section，we denotef(x，s)=g(x)(s+)q-1and.Then we have

Lemma 2.1Let{km}?(0，∞) be a sequence such thatkm→k∈(0，∞]，and letbe a sequence such thatum?ufor someu∈.Then

(i) ifk＜∞，

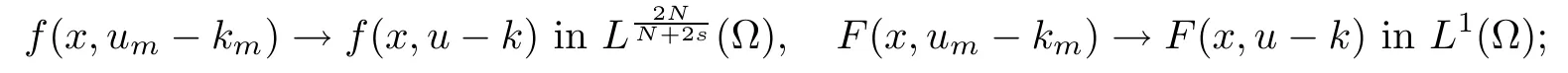
(ii) ifk=∞，

ProofBy the Vitali Convergence Theorem，it is easy to check the result.For more details，see Lemma 1 of[4]. □

Now，we prove thatJksatisfies thePScondition below the energy threshold.

Lemma 2.2Letk∈(0，∞) and.ThenJksatisfies thePScondition at levelck.

ProofLet{um}be aPSsequence ofJk.Then we have

Ifq=2，for anyand (G)，we have

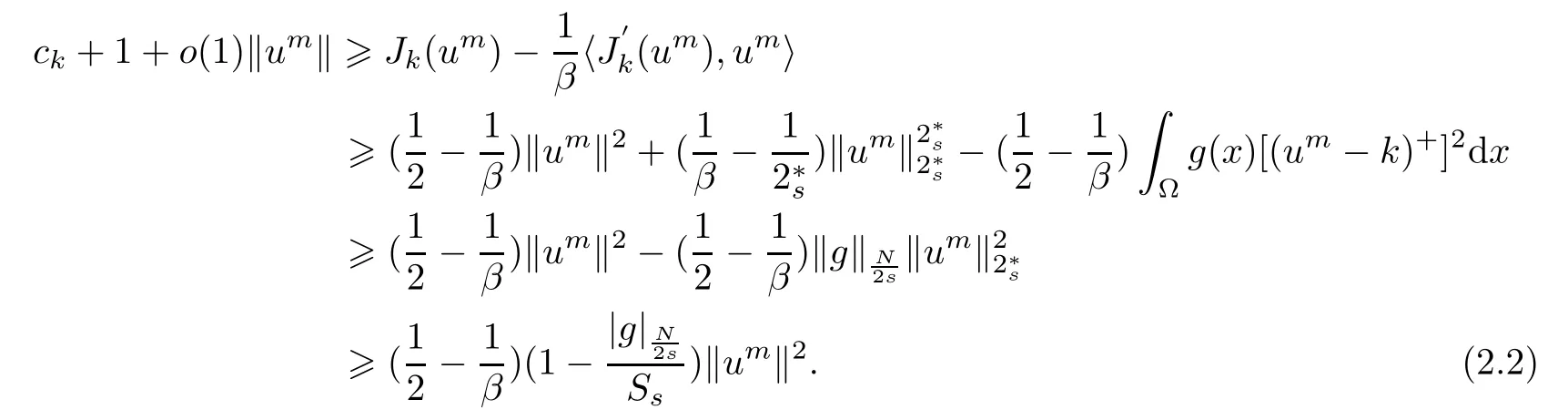
From (2.1) and (2.2) we know that{um}is bounded inThus，there existsu∈such thatum?u(up to a subsequence) and.Thus，we get

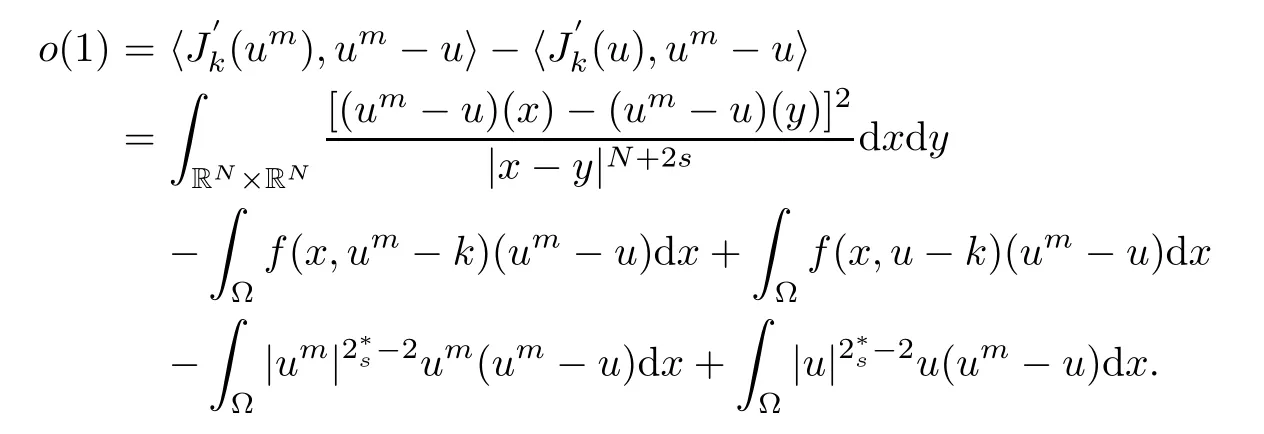
By Lemma 2.1，(1.1) and the Brezis-Lieb Lemma，we get

Hence，from (2.3)，we can know that either

Now we prove，by contradiction，that the second of these cases cannot occur.If it held，that is，

then，by Lemma 2.1 and the first equality of (2.3)，we would get

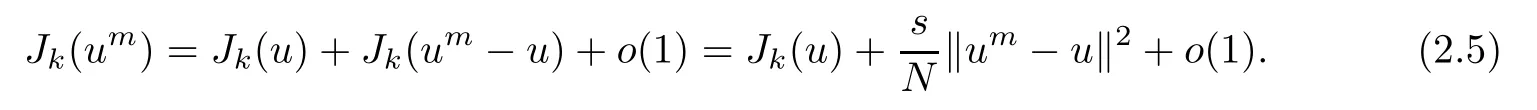
Hence，from (2.4)，(2.5) and (2.6)，we get

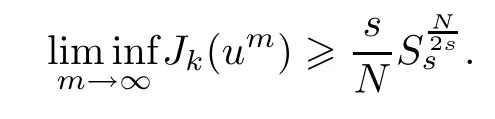
This stands in contradiction with.Therefore，we get ‖um-u‖→0. □

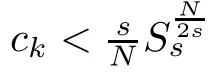
Next，we want to estimate the mountain pass valueckdefined by (1.5).We have

Lemma 2.3For anyk∈(0，∞)，we have

ProofFrom (G)，there exist a positive constantband a nonempty open setA?Ω such that

Without loss of generality，we may assume that 0∈A.We take a cut-offfunctionη∈C∞0(A) such that 0≤η≤1 inA，η=1 inB(δ) andη=0 inAB(2δ)，whereδis a small positive constant.We denote

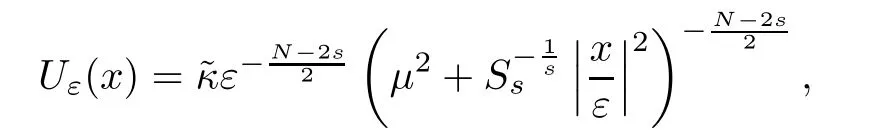
If (2.8) does not hold，then there existstε＞0 such that

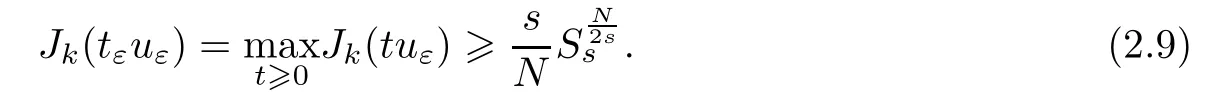
From (2.9)，it is easy to check thattεis upper and lower bounded.From[11]，we have that

Thus，by (2.10)，we see that

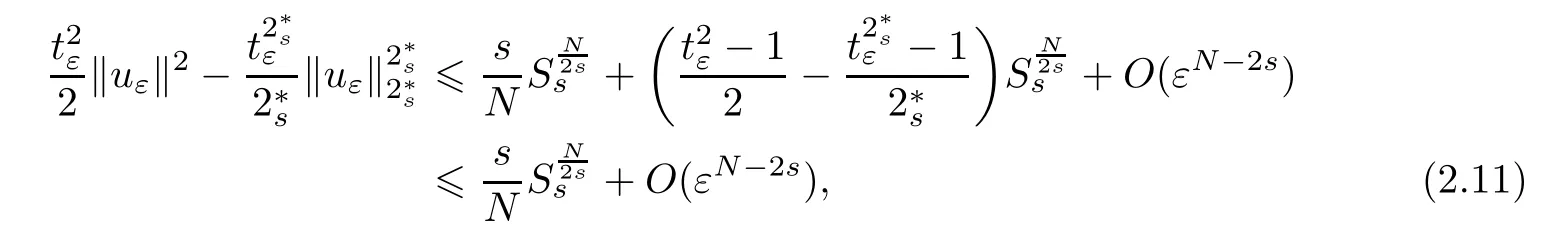
and the second inequality follows from

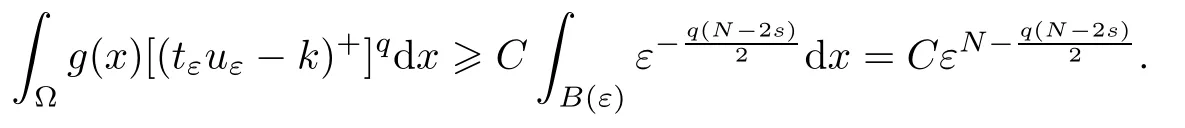
From (1.2)，we know that ifN＞2sandN4s，then.Thus，by (2.11)，we get

Finally，whenN=4s，ifq＞2，then，so we also get (2.12).Ifq=2，then for allk＞0，there existsCk＞0 such that forεsmall，Therefore，we have

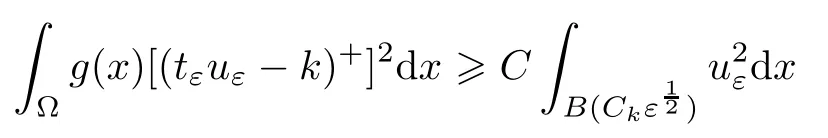
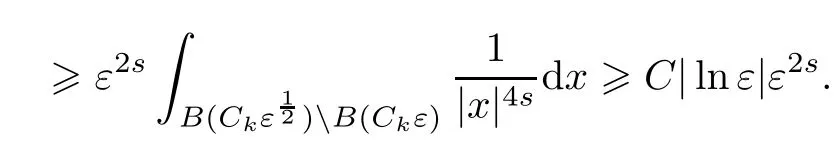
Using (2.11) again，we get

From (2.12) and (2.13)，we reach a contradiction with (2.9).Thus we have proved (2.8)，and□

From previous lemmas，we know that mountain pass solutions of (Pk) exist with energy belowThus we have

Lemma 2.4For anyk∈(0，∞)，there exists a mountain pass solutionukof (Pk).

ProofIt is easy to check thatJksatisfies the mountain pass geometry.Therefore，there exists aPSsequence{um}ofJk.From Lemmas 2.2 and 2.3，we know that there exists a mountain pass solutionuk∈M of (Pk).Thus we can get (-△)suk(x)≥0 in Ω.Moreover，uk＞0 in Ω. □

Now we want to prove that mountain pass solutions are uniformly bounded in(Ω).

Lemma 2.5There exists a constant Λ＞0 such that，for anyk＞0 and a mountain pass solutionukof (Pk)，we have ‖uk‖≤Λ.

ProofThe result follows directly from (2.1) and (2.2). □

Finally，we want to prove that the weak limit of mountain pass solutions is also a solution.

Lemma 2.6Let{km}?(0，∞) be a sequence such thatkm→k∈(0，∞]and{ukm}is a sequence of mountain pass solutions of (Pkm).Then there existsu∈(Ω) such thatukm?uin(Ω)，up to a subsequence.Moreover，usolves (Pk).

ProofBy Lemma 2.5，we know that{ukm}is uniformly bounded in(Ω).Therefore，there existsu∈(Ω) such thatukm?uin(Ω)，up to a subsequence.Sincefor anyφ∈(Ω)，we have

By Lemma 2.1，lettingkm→k，we get thatusolves (Pk). □

3 Proof of Main Results

In this section，we prove our main results.For the sake of completeness，we sketch the proof of Theorem 1.2;see also[14]for star-shaped domains.

Proof of Theorem 1.2From (1.2) and (2.11)，we get

We claim that for any nontrivial solutionuof (P∞)，we have

Proof of claim:sinceuis a nontrivial solution of (P∞)，then

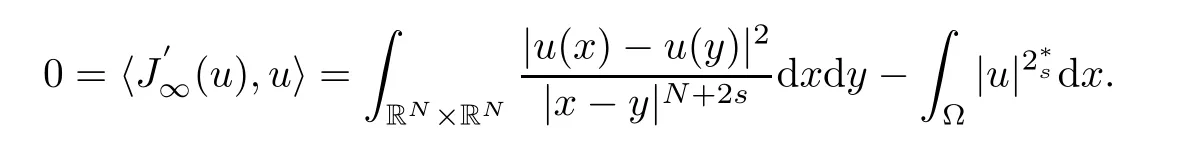
Thus，we get

On the other hand，by (1.1)，we know that

The claim follows from (3.3) and (3.4).Therefore，the result follows from (3.1) and (3.2). □

We will now give some lemmas which will be later used.

Lemma 3.1For anyk∈(0，∞)，ifukis a mountain pass solution of (Pk)，then there existsλ＞0 such that the segmentsatisfieswhereλis independent ofk.

ProofFirst，we claim that there existsτ＞0 such that

From (2.1) and (2.2)，we have

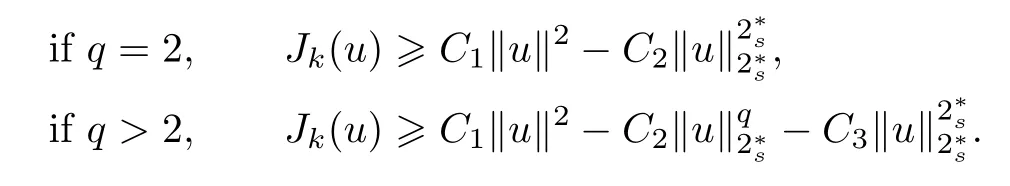
Therefore，there existρ＞0 andτ＞0 small such thatJk(u)≥τif ‖u‖=ρandJk(u)＞0 if ‖u‖＜ρ.Thus，by (1.5)，we can get (3.5).

Thus，for anyk∈(0，∞)，there existsδ＞0 such that

Finally，we want to prove that，for anyk∈(0，∞)，we have

Let Φk(t)=Jk(tuk).Using=0 we can get

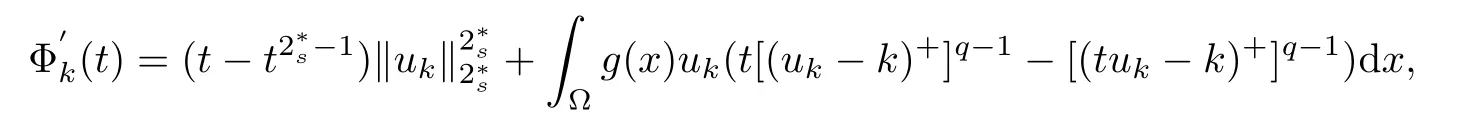
so Φk(t) is increasing in (0，1) and decreasing in (1，∞).Therefore，

Let Λ be in Lemma 2.5 and letδbe in (3.6).We denoteThen we have

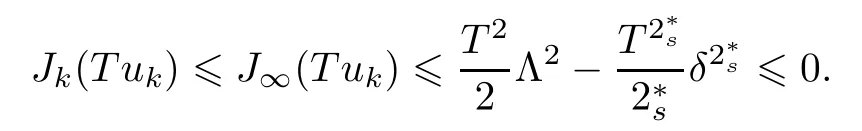
Now，takingλ=ΛT，we can get

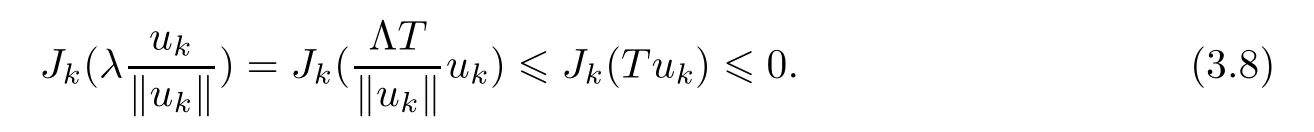
Thus，the result follows from (3.7) and (3.8). □

Next we prove that the mountain pass valueckis continuous with respect tok.The conclusion is as follows:

Lemma 3.2Let{km}?(0，∞) be a sequence such thatkm→k＜∞.Thenckm→ck.Moreover，for any compact intervalsI?(0，∞)，there existsδI＞0 such that ifk∈I，then

ProofFirst，we claim that for any bounded subset in(Ω)，we have

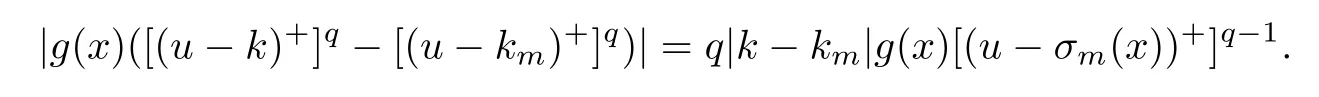
Hence，we have

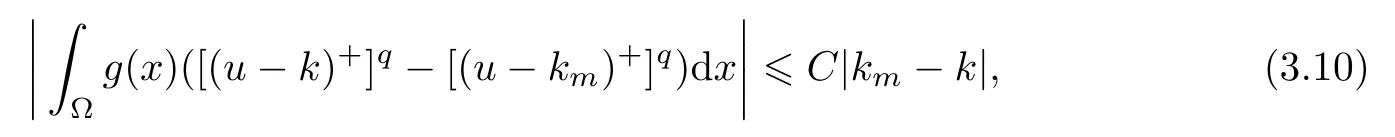
whereCdepends onR.Thus the claim follows from (3.10).Denote Σ:={γj|j=k1，k2，...orj=k}，whereγjis introduced as in Lemma 3.1，and we know that Σ?Bλ.Thus，by (3.9)，we can get

Note thatI?(0，∞) is compact and that the mapis continuous.Thus the maximumonIcan be attained.By Lemma 2.3，we know thatfor anyk∈I.Therefore，we take□

Now we prove Theorem 1.3.

Proof of Theorem 1.3By Lemma 2.4，we have proved the existence of mountain pass solutions of (Pk).Now we want to prove the existence of.Assume that ‖uk‖∞≤kand thatukis a mountain pass solution of (Pk).Then (uk-k)+≡0，souksolves the (P∞).This contradicts Theorem 1.2.Therefore，‖uk‖∞＞k，and Ω(uk) is not empty.We can take∈Ω(uk).

From Lemma 2.6，we know thatusolves (Pk).Next we want to prove thatuis a mountain pass solution of (Pk).By Lemma 2.1，we have

Whenk→∞，the subcritical perturbation term will vanish;we want to prove that the energy of mountain pass solutions tends to critical energy threshold.

Lemma 3.3Letukbe the mountain pass solution of (Pk) fork∈(0，∞).Then

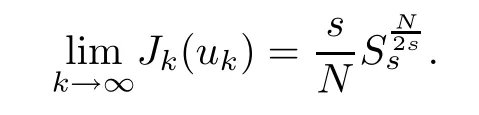
ProofUsing Lemma 2.6，we can see thatuk?uinand thatusolves the (P∞).From Lemma 2.1 and (1.1)，we have

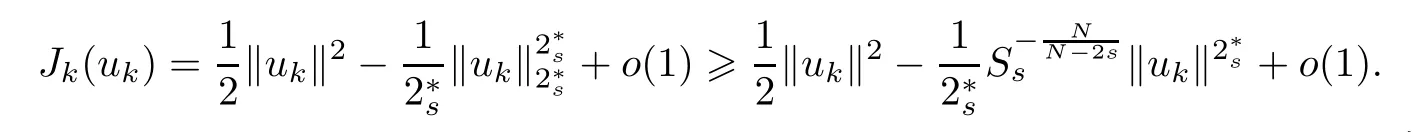
Thus we know that the-sphere of radiusseparates 0 and N.By (1.5)，we have

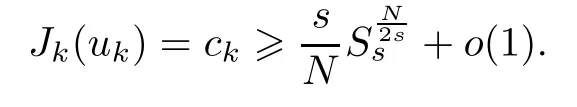
On the other hand，from Lemma 2.3，we get

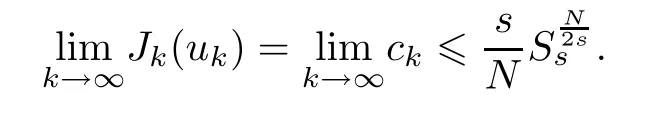
The proof is complete. □

With the previous lemmas we can prove the last two results as follows:

Proof of Theorem 1.4By Lemma 2.6，we know that there existsu∈(Ω) solves (P∞) and thatuk?uin.Next，we will proveu≡0.InsertingintoJk，we get

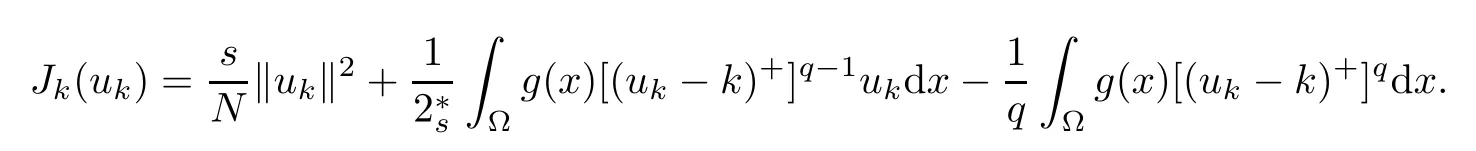
By Lemma 2.1 and Lemma 3.3，we get thatSince，we have

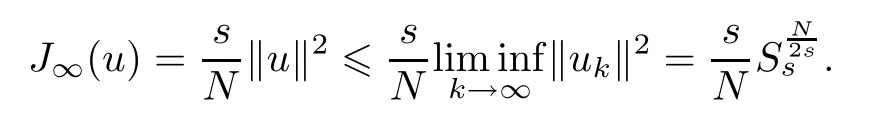
Therefore，using the claim of the proof of Theorem 1.2，we can infer thatu≡0.Finally，using Theorem 1.2 in[7]，we can get

where J is at most countable，xj∈and

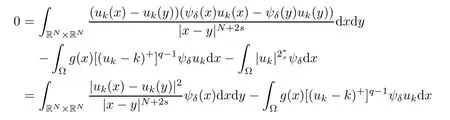
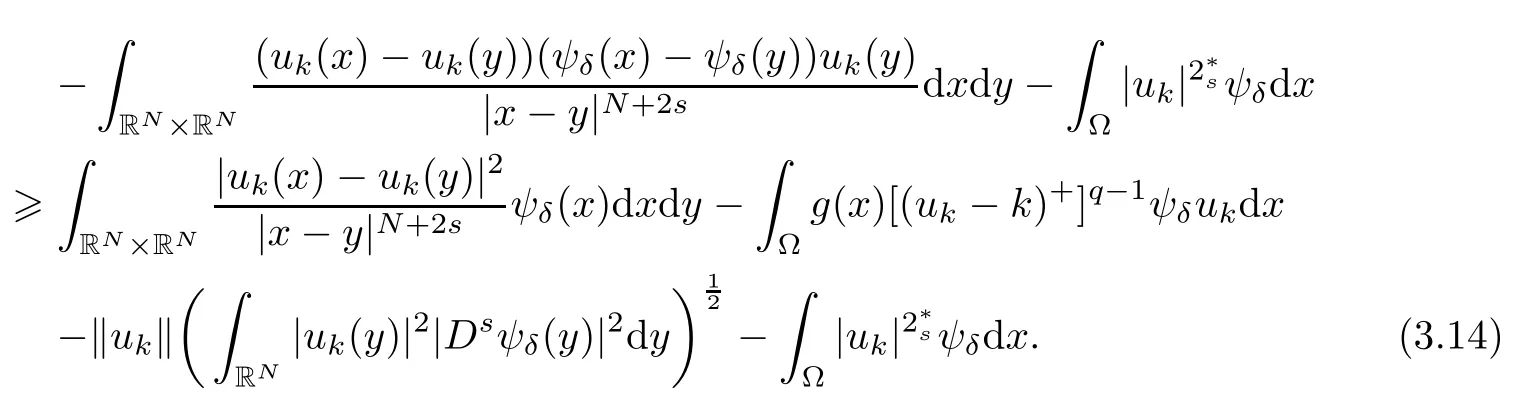
Using Lemma 2.1，we know that the second term of (3.14) tends to zero.The third term of (3.14) is more complicated，however，because of the nonlocal gradient|Dsψδ(y)|2.By Corollary 2.3 in[7]，we have

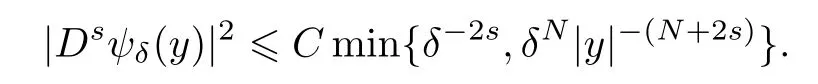
Then we can obtain

The first term can be estimated as follows:

The second term can be estimated as follows:

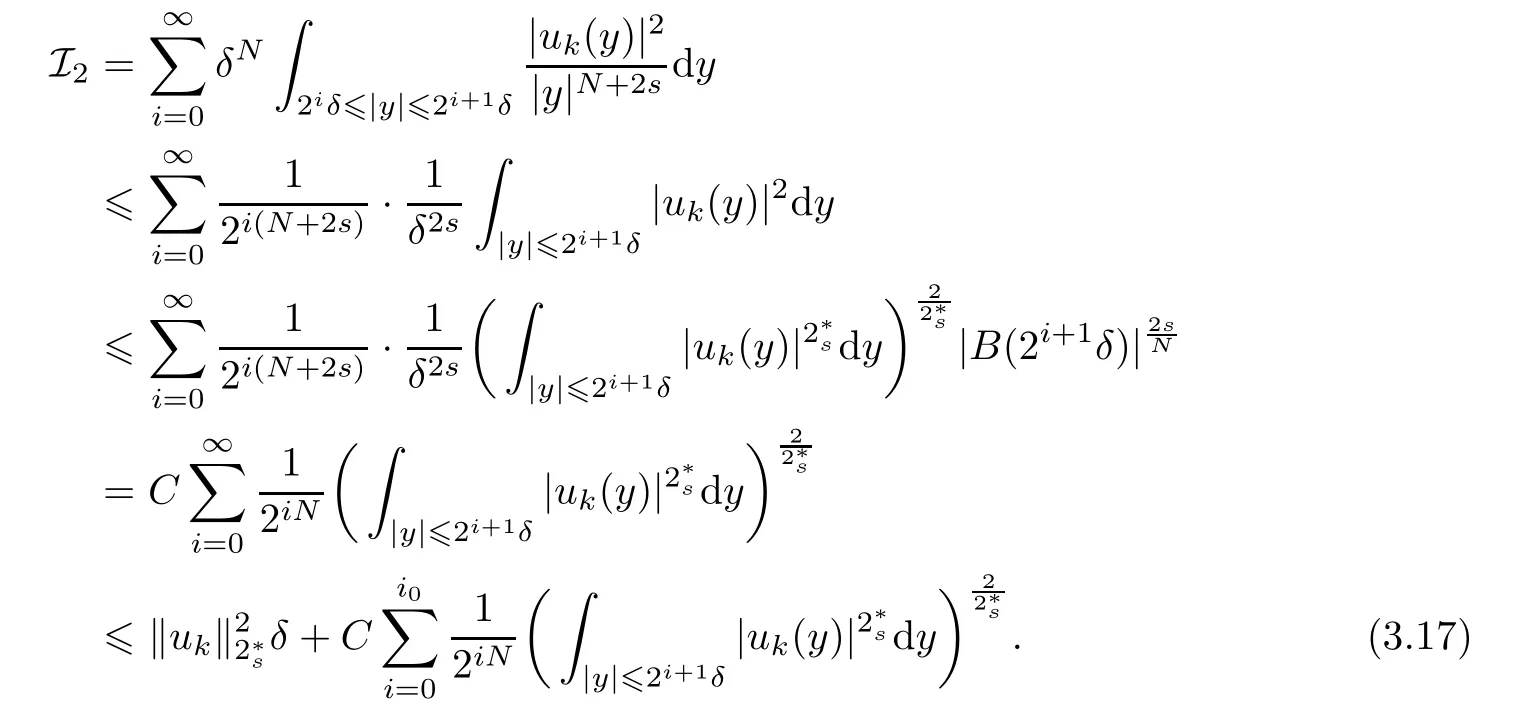
The last inequality holds becauseis convergence.Thus there exists an integeri0such thatFrom (3.14)，(3.15)，(3.16) and (3.17)，lettingk→∞，we can get

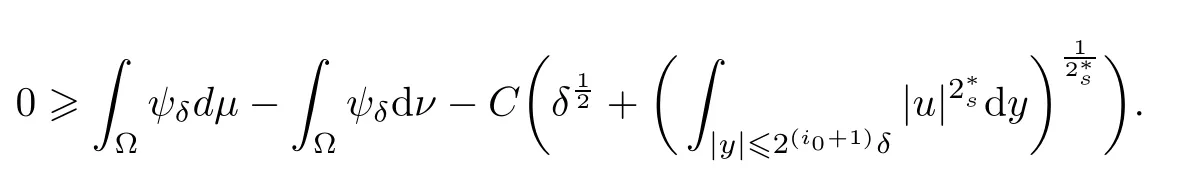
Then lettingδbe small，we get

Therefore，ifνj0，from (3.13) and (3.18)，we can conclude thatFinally，using Lemma 3.3 and (3.11)，we know that there exists a unique indexj0such thatThus we may choose a subsequence{ukm}such that the sequencesconverge to the same pointx0∈.□

Now we can prove Theorem 1.5.

Proof of Theorem 1.5Lettingukbe any mountain pass solution of (Pk)，we argue by contradiction.If Ω(uk)∩Ωg=?，theng(x)[(uk-k)+]q-1≡0，which infers thatuksolves the (P∞).This contradicts Theorem 1.2.Thus for allk∈(0，∞)，there existsand similarly to Theorem 1.4，the limitx0ofbelongs to Ωg. □

AcknowledgementsThe authors would like to thank Professor Shuangjie Peng very much for stimulating discussions and helpful suggestions on the present paper.