永磁直線同步電動機迭代超螺旋滑模控制
賀玉曉 王麗梅
永磁直線同步電動機迭代超螺旋滑模控制
賀玉曉 王麗梅
(沈陽工業大學電氣工程學院,沈陽 110870)
針對永磁直線同步電動機(PMLSM)伺服系統易受周期性擾動、參數攝動、摩擦力等不確定性因素影響而導致位置跟蹤精度下降的問題,本文提出一種迭代超螺旋滑模控制方法。利用超螺旋滑模控制抑制不確定性因素的影響,增強系統的魯棒性;迭代學習用于補償周期性擾動并采用一種新型的學習律削弱系統抖振。基于Lyapunov穩定性理論,對控制系統的穩定性進行分析證明。仿真結果表明,所提控制方法能夠提高PMLSM伺服系統魯棒性,提高位置跟蹤精度。
永磁直線同步電動機(PMLSM);周期性擾動;迭代超螺旋滑模控制;位置跟蹤
0 引言
永磁直線同步電動機(permanent magnet linear synchronous motor, PMLSM)采用直接驅動的方式,與旋轉電動機相比,具有熱損耗低、精度高、零傳動間隙等優點,因此,廣泛應用于高速高精密數控加工系統[1-2]。但是,PMLSM受端部效應導致的周期性推力波動、摩擦力、負載擾動及參數攝動等不確定性因素的影響,導致其位置跟蹤性能下降[3-4]。因此,如何解決不確定性因素對系統的負面影響,提高系統的魯棒性,獲得更高的位置跟蹤精度是亟需解決的關鍵問題。
為了提高PMLSM的位置跟蹤精度,國內外學者對各種不同的控制策略進行了研究。滑模控制(sliding mode control, SMC)是一種非線性控制,具有實現簡單、響應快、魯棒性強等優點,但是為了確保被控系統的強魯棒性,切換增益需選擇較大的值,較大的切換增益會產生抖振現象[5-6]。文獻[7]為了保證PMLSM的位置跟蹤精度,采用滑模控制抑制系統不確定性因素及外部擾動,但為了削弱抖振的影響引入了概率型模糊神經網絡觀測不確定性邊界,使系統的魯棒性有所下降。超螺旋滑模控制(super-twisting sliding mode control, STSMC)是一種二階滑模控制方法,所需信息少,且與螺旋算法、漂移算法、準連續和次優算法等二階滑模算法相比,超螺旋算法只需滑模變量不需滑模變量的一階導數,且控制器設計簡單[8],能在同時保證系統跟蹤精度和魯棒性的前提下削弱傳統滑模控制的抖振[9]。文獻[10]利用超螺旋滑模控制使伺服系統獲得高質量的跟蹤精度和穩定性,避免了較高的切換增益導致的抖振現象,且所需調節的參數少,但是未考慮周期性推力波動的影響。文獻[11]將超螺旋滑模控制應用于永磁直線伺服系統,使伺服系統對不確定性參數的變化具有強魯棒性,但是忽略了摩擦力的影響。
迭代學習控制(iterative learning control, ILC)利用期望位置與實際輸出位置的誤差不斷修正控制信號,能夠顯著抑制具有重復性質的擾動,提高系統的跟蹤性能,適用于建模難、位置跟蹤精度要求高的動力學系統[12-13]。文獻[14]為了減小周期性推力波動對PMLSM位置跟蹤精度的影響,利用迭代學習的學習能力補償周期性推力波動,能夠有效提高伺服系統的位置跟蹤精度。文獻[15]針對永磁直線電動機的位置跟蹤控制,將摩擦力視為周期性擾動,提出基于迭代學習的復合控制方法,迭代學習用于補償周期性擾動,能夠顯著減小周期性擾動對位置跟蹤精度的影響。
綜合考慮以上因素,本文提出一種迭代超螺旋滑模控制(ILC-STSMC)方法。該方法采用一種由迭代學習律和廣義超螺旋滑模控制器組成的控制結構,超螺旋滑模控制保證系統對不確定性擾動具有較強的魯棒性,迭代學習補償周期性擾動,削弱系統抖振,在迭代學習律中使用符號函數保證滑模面快速收斂到零。最后,通過仿真對所提控制策略的有效性加以驗證。
1 PMLSM數學模型
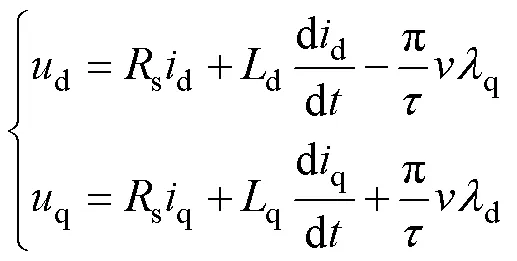
其中
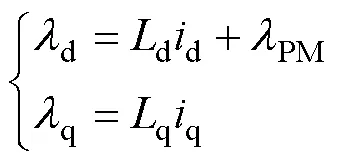
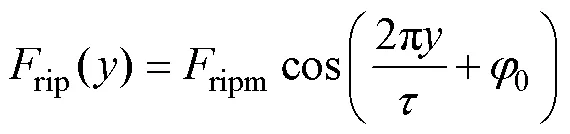
理想情況下,PMLSM的電磁推力為


PMLSM的動子的運動方程為
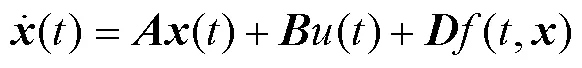
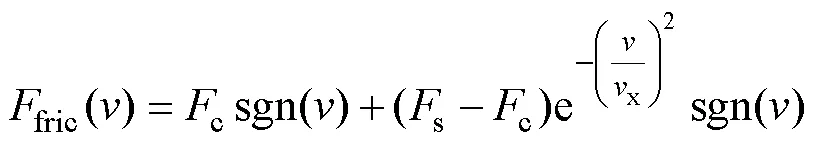
2 迭代超螺旋滑模位置控制器的設計
2.1 超螺旋滑模控制器的設計
在PMLSM系統狀態未知的情況下,將式(5)表示為
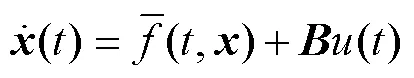

首先,對滑模面和控制律進行設計。
定義滑模面為
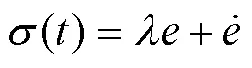
由式(8)和式(10)可得
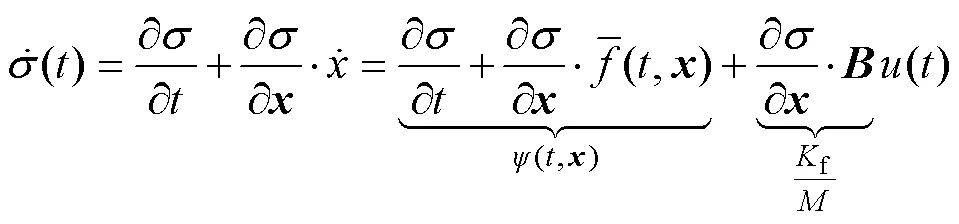
因此,式(11)可以表示為
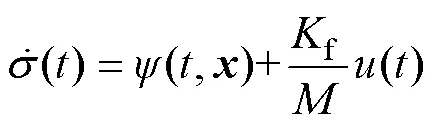
其次,設計滑模控制律,廣義的超螺旋控制律表示為

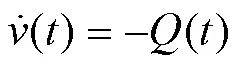
其中

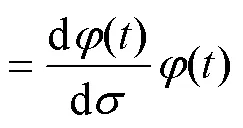
2.2 迭代超螺旋滑模控制器的設計
為了提高位置跟蹤精度,削弱系統抖振,在超螺旋滑模控制器的基礎上,引入迭代學習律補償周期性擾動,進而減小系統不確定性的邊界。
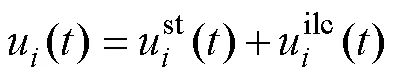
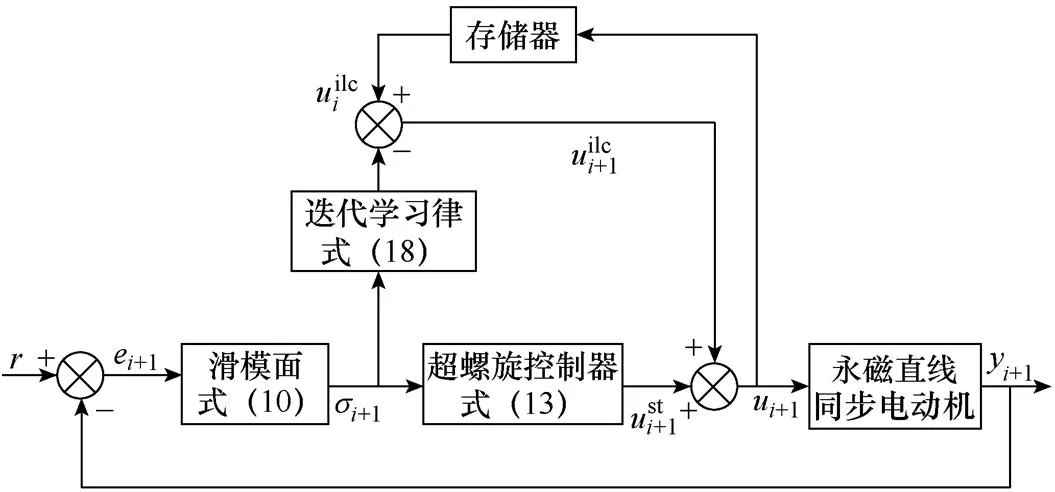
圖1 迭代超螺旋滑模控制框圖
采用一種利用超螺旋滑模控制器中的滑模面和積分項信息的迭代學習律。因此,控制器設計為
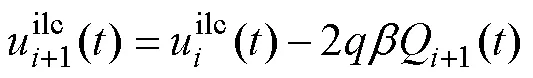
2)每次迭代的初始狀態是相同的。
3)每次迭代的參考信號是相同的。
由式(11)可得
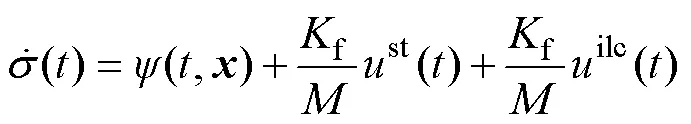
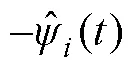
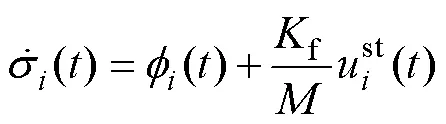
因此,迭代學習將補償不確定性,使超螺旋滑模控制能在不確定性未知的情況下將滑模面趨近于零。
2.3 穩定性分析

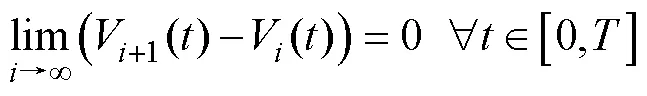
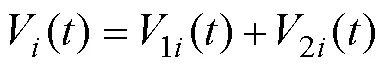


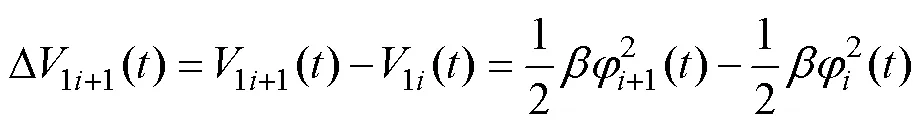
由式(16)得
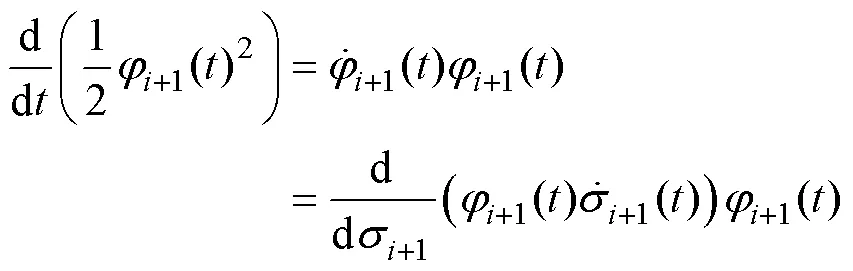
將式(13)、式(14)、式(20)和式(26)代入式(25)得
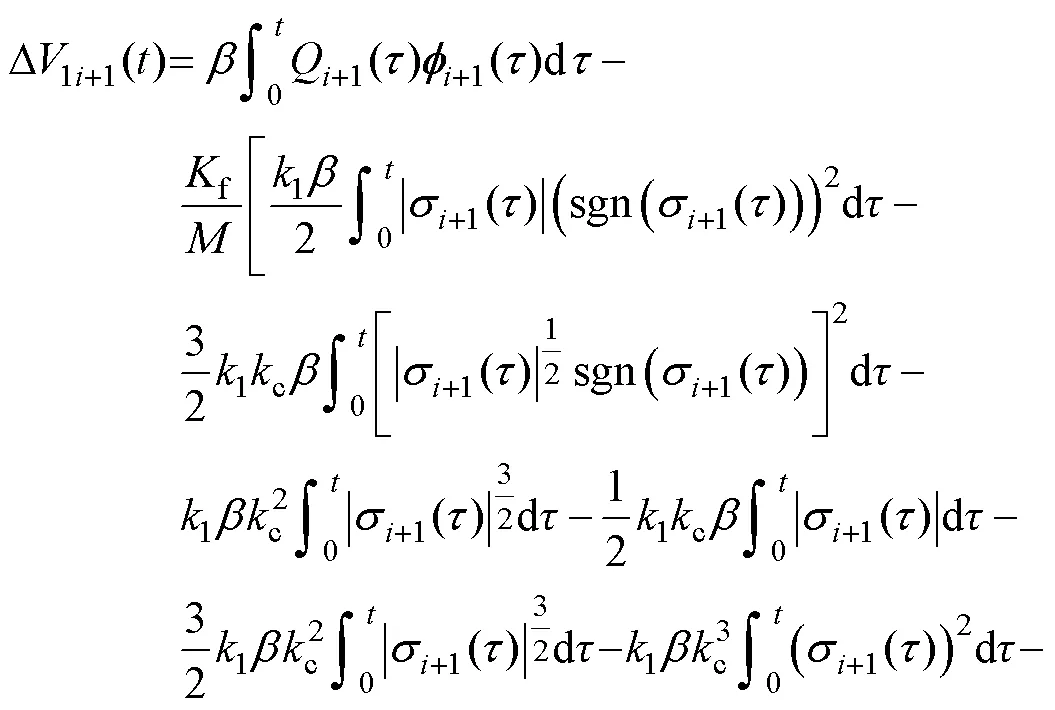
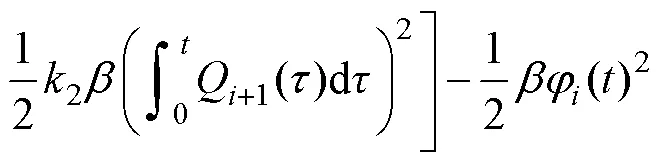

將式(18)代入式(28)得
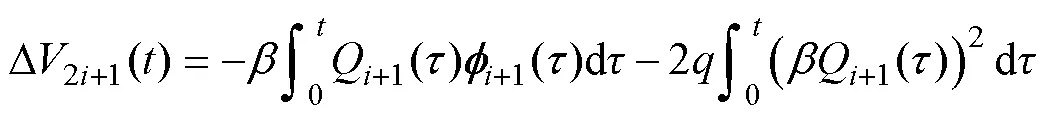
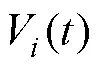
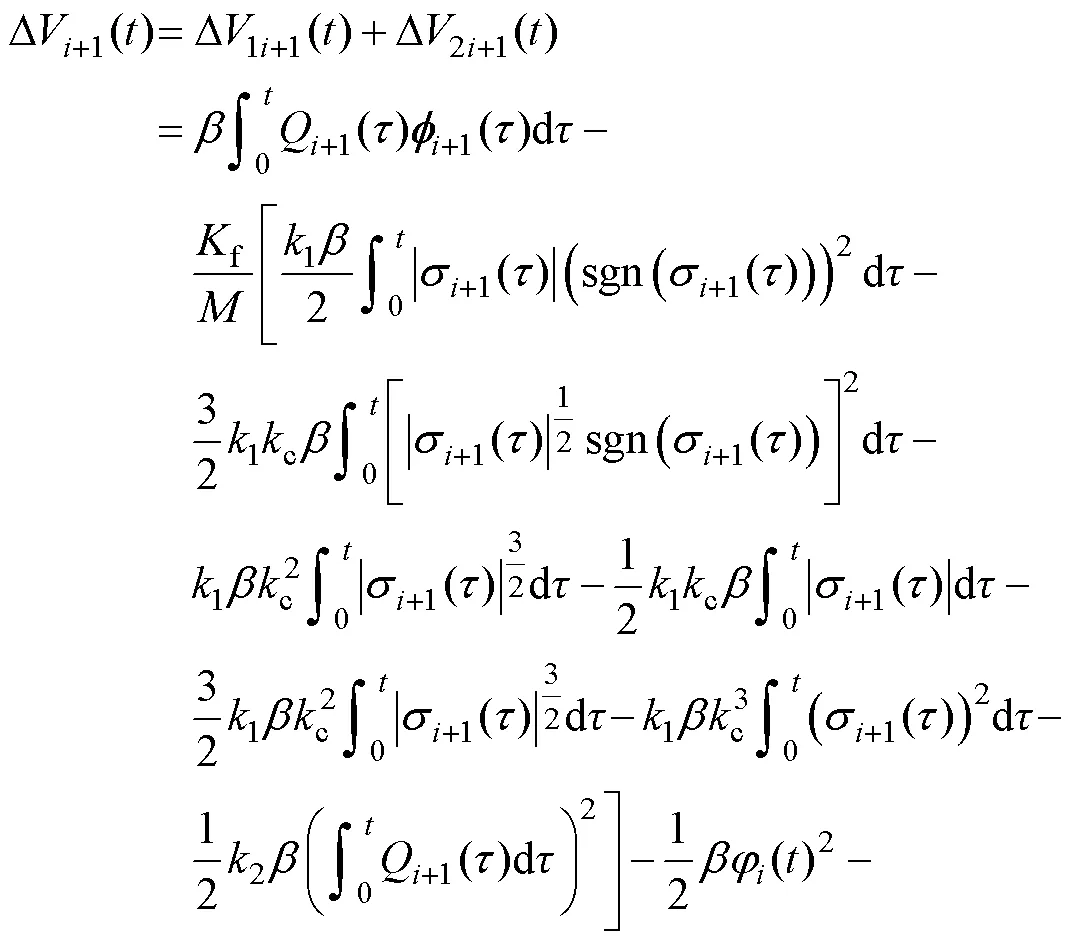
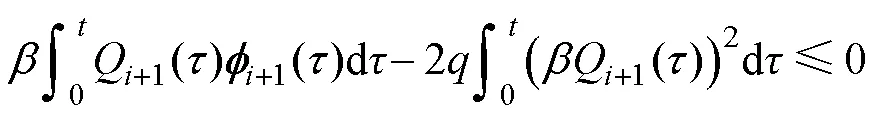
綜上所述,永磁直線同步電動機伺服控制系統框圖如圖2所示,PMLSM電流控制采用PI控制。

圖2 永磁直線同步電動機伺服控制系統框圖
3 仿真結果與分析
首先采用STSMC進行仿真,穩態后在3.5s加30N負載阻力。圖3為期望輸出與實際輸出,圖4為基于STSMC的位置跟蹤誤差。由圖4可知,在3.5s突加負載后基于STSMC的位置跟蹤誤差會出現波動并能夠快速恢復到穩態。
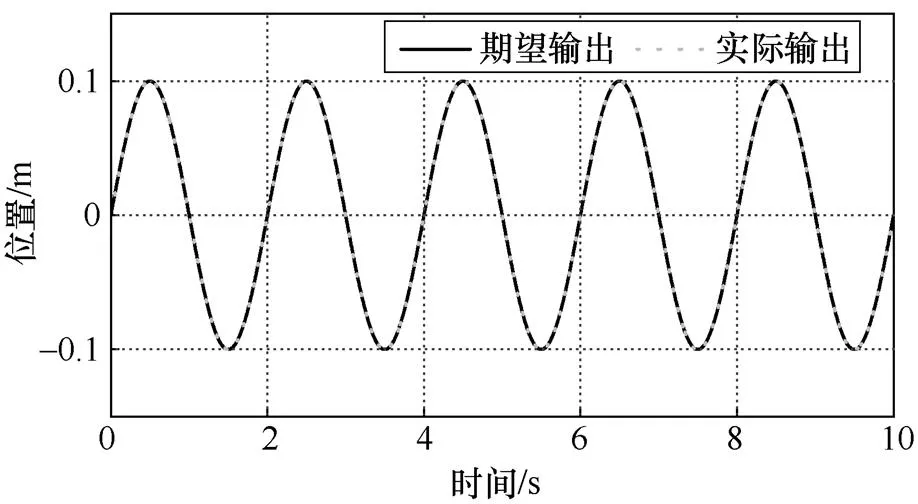
圖3 期望輸出與實際輸出曲線

圖4 基于STSMC的位置跟蹤誤差曲線
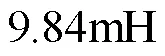
因為迭代學習律中引入了式(16),所以如果參數選取過大可能加劇抖振,因此參數選取較小值進行仿真。由圖5可知,參數偏大(如=1.8、2.1、2.4)或者偏小(如=1.2)均會不同程度地降低誤差收斂速度,=1.5時誤差收斂速度最快且控制精度也較高。因此取參數1.5。
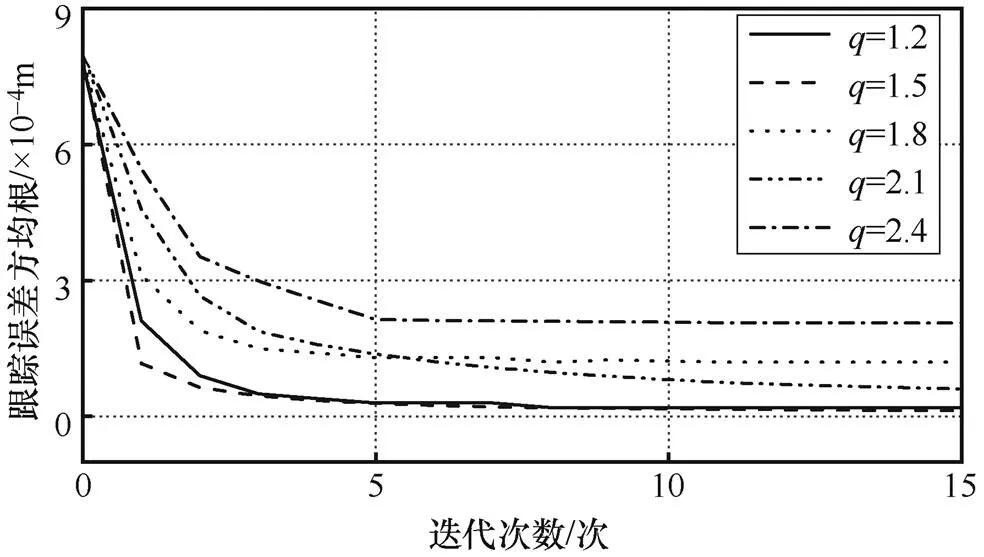
圖5 參數q對ILC-STSMC收斂性能影響
圖6為迭代15次后產生的估計信號和實際信號及估計信號和實際信號的誤差。由圖6可知,所設計的迭代學習算法能夠產生較精確的估計信號。圖7為最后一次迭代的期望輸出與實際輸出,圖8為其他參數不變當定子電感變化時基于ILC-STSMC的位置跟蹤誤差。由圖8可知,在3.5s突加負載后基于ILC-STSMC的位置跟蹤誤差會出現波動并能夠快速恢復到穩態。

圖6 估計信號、實際信號及誤差
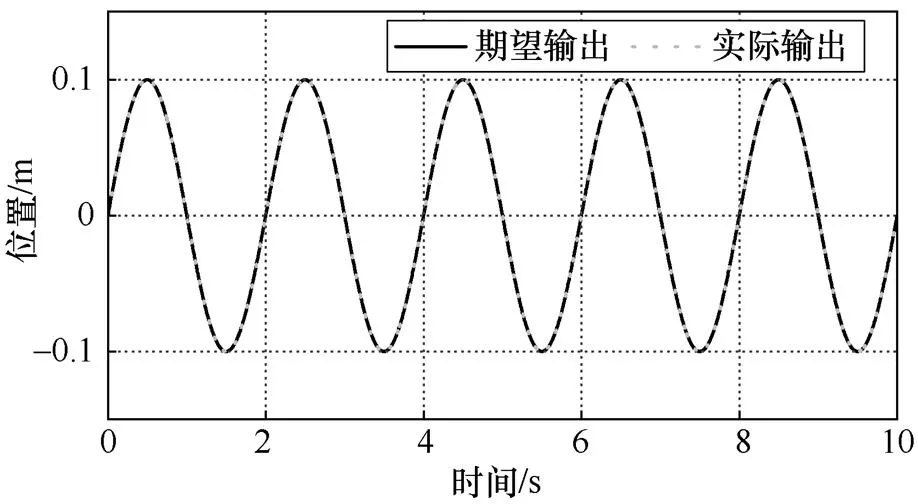
圖7 最后一次迭代的期望輸出與實際輸出曲線
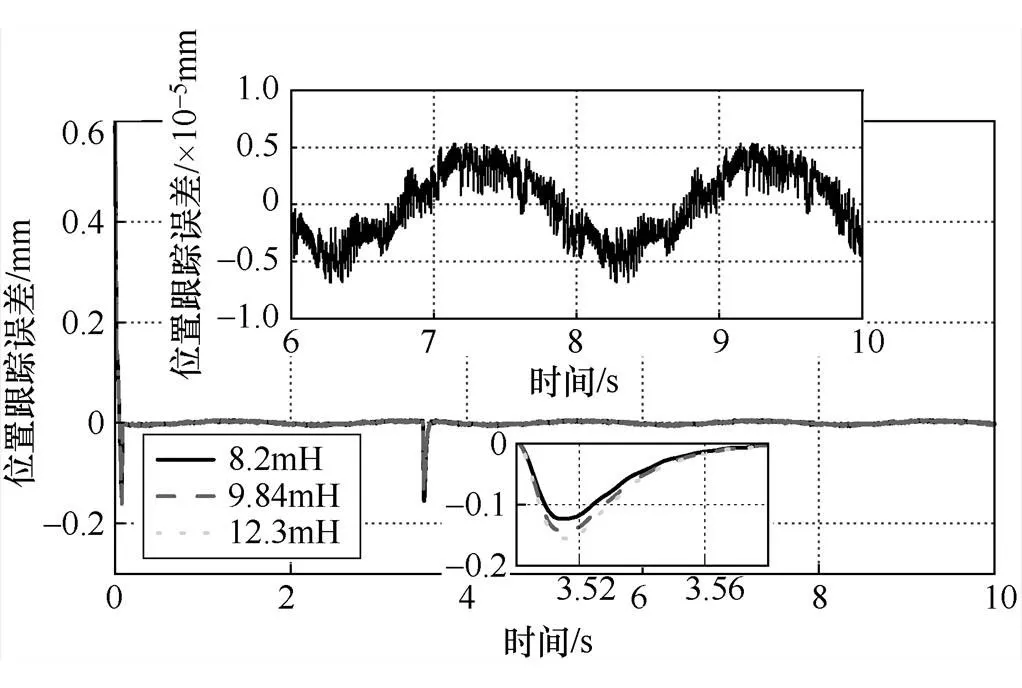
圖8 基于ILC-STSMC的位置跟蹤誤差曲線
4 結論
為了提高PMLSM伺服系統位置跟蹤精度和魯棒性,本文提出了一種迭代超螺旋滑模控制方法,該控制方法是由超螺旋滑模控制器和迭代學習律組成的二自由度控制結構。超螺旋滑模控制器保證系統的魯棒性,迭代學習補償周期性擾動并利用一種新型的學習律削弱系統抖振。仿真結果表明,與超螺旋滑模控制器相比,在周期性擾動和突加負載的狀態下,基于ILC-STSMC控制器的永磁直線同步電動機伺服系統具有更好的位置跟蹤性能。
[1] 王璨, 李國沖, 楊桂林, 等. 基于生物智能環狀耦合的嵌入式永磁同步直線電機高精度位置協同控制研究[J]. 電工技術學報, 2021, 36(5): 935-943.
[2] 盧琴芬, 沈燚明, 葉云岳. 永磁直線電動機結構及研究發展綜述[J]. 中國電機工程學報, 2019, 39(9): 2575-2588.
[3] 張圳, 王麗梅. 永磁同步直線電機自組織概率型模糊神經網絡控制[J]. 電氣技術, 2020, 21(12): 1-5, 16.
[4] 劉樂, 宋紅姣, 方一鳴, 等. 基于ELM的永磁直線同步電機位移跟蹤動態面反步滑模控制[J]. 控制與決策, 2020, 35(10): 2549-2555.
[5] 付東學, 趙希梅. 永磁直線同步電機自適應非奇異快速終端滑模控制[J]. 電工技術學報, 2020, 35(4): 43-49.
[6] 張育增, 周睿智, 李帥. 永磁同步直線電機模糊滑模速度控制研究[J]. 電氣技術, 2020, 21(12): 23-29.
[7] CHEN S Y, CHIANG H H, LIU T S, et al. Precision motion control of permanent magnet linear syn- chronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752.
[8] 劉暢, 楊鎖昌, 汪連棟, 等. 基于快速自適應超螺旋算法的制導律[J]. 北京航空航天大學學報, 2019, 45(7): 1388-1397.
[9] CHALANGA A, KAMAL S, FRIDMAN L M, et al. Implementation of super-twisting control: super- twisting and higher order sliding-mode observer-based approaches[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(6): 3677-3685.
[10] HOU Qiankang, DING Shihong. GPIO based super- twisting sliding mode control for PMSM[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(2): 747-751.
[11] EL-SOUSY F F M, ALENIZI F A F. Optimal adaptive super-twisting sliding-mode control using online actor- critic neural networks for permanent-magnet syn- chronous motor drives[J]. IEEE Access, 2021, 9: 82508-82534.
[12] 楊亮亮, 王杰, 王飛, 等. 基于最優控制迭代學習的直線伺服系統振動抑制研究[J]. 機械工程學報, 2019, 55(15): 217-225.
[13] 方一鳴, 張文健, 李建雄, 等. 伺服電機驅動的連鑄結晶器振動位移系統前饋+迭代學習復合控制[J]. 電機與控制學報, 2020, 24(12): 130-141.
[14] SONG Fazhi, LIU Yang, XU Jianxin, et al. Iterative learning identification and compensation of space- periodic disturbance in PMLSM systems with time delay[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7579-7589.
[15] HUI Yu, CHI Ronghu, HUANG Biao, et al. Extended state observer-based data-driven iterative learning control for permanent magnet linear motor with initial shifts and disturbances[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1881-1891.
[16] 張康, 王麗梅. 基于周期性擾動學習的永磁直線電機自適應滑模位置控制[J]. 電機與控制學報, 2021, 25(8): 132-141.
Iterative super-twisting sliding mode control for permanent magnet linear synchronous motor
HE Yuxiao WANG Limei
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870)
In order to solve the problem that the position tracking accuracy of permanent magnet linear synchronous motor (PMLSM) servo system is affected by periodic disturbance, parameters change, friction and other uncertain factors, an iterative super-twisting sliding mode control method is proposed. The super-twisting sliding mode control is used to restrain the influence of uncertain factors and enhance the robustness of the system. Iterative learning is used to compensate periodic disturbance and a new learning law is adopted to reduce chattering. Based on Lyapunov stability theory, the stability of the control system is analyzed and proved. Simulation results show that the proposed control method can improve the robustness and improve position tracking accuracy of PMLSM servo system.
permanent magnet linear synchronous motor (PMLSM); periodic disturbance; iterative super-twisting sliding mode control; position tracking
2022-01-24
2022-02-25
賀玉曉(1995—),女,山東泰安人,碩士研究生,主要研究方向為永磁直驅伺服系統及其控制。
國家自然科學基金項目(51875366)

