魚類集群運動的注意力模型研究

趙佳佳，劉 磊

（上海理工大學管理學院，上海 200093）

0 引言

自然界中隨處可見成群結隊覓食的蟻群［1］、編隊遷徙的鳥群［2］、洄游的魚群［3-4］等，動物之間采用簡單交互規則便能實現信息傳遞，這種自組織的涌現行為給人工集群復雜系統的靈活控制提供了有益參考。科學家通過對自然界生物的長期觀察，研究出經典的生物啟發交互算法，如Aoki 模型［5］、Vicsek 模型［6］和Couzin 模型［7］等，并通過簡單自推進粒子（Self-propelled Particle，SPP）模型［8］仿真驗證集群運動的組織協調性，進而應用于大規模人造集群系統的控制中［9-10］。

隨著自動跟蹤技術的發展，加之當前計算機技術為圖像處理提供了足夠算力［11］，生物運動數據得以被大規模采集［12］，集群運動的數據驅動建模更加便捷高效。在生物學和物理學領域，集群運動的研究重點集中在建模和仿真方面［13］。然而，傳統的數據驅動建模多為人工設計，且強烈依賴于人類直覺和各種先驗假設的數學模型結構［14］，當面對真實生物運動數據時，傳統的數學模型結構難以展現和解釋集群運動的復雜行為。

近年來，以深度學習為代表的人工智能技術蓬勃發展，為復雜系統的集群研究提供了有效方案［15］。深度神經網絡使集群運動數據交互模型的提取成為可能［16］，但由于其具有臭名昭著的黑盒特性，使得進一步研究集群內部個體交互的信息傳播路徑變得十分困難。

目前，以Transformer 為代表的注意力機制逐漸成為深度學習領域的主流方法和研究熱點。本文將注意力機制與生物集群行為相結合，通過分析真實魚群運動數據，訓練出泛化性能良好的可預測和解釋復雜系統隱藏交互行為的深度注意力網絡模型，并應用于真實魚群運動研究與智能體仿真實驗中，從而為實現更大規模的靈活分布式系統控制奠定基礎。

1 相關研究

1.1 長短期記憶模型

復雜系統的行為數據大多表現為時間序列，序列模型便是為此類數據建模設計的。傳統的循環神經網絡［17］（Recurrent Neural Network，RNN）雖然能夠解決序列數據問題，但在處理長序列時存在嚴重的梯度消失和梯度爆炸問題。

為了減輕RNN 中的梯度消失現象，長短期記憶（Long Short-Term Memory，LSTM）網絡［18］應運而生。LSTM 中添加了額外的隱含狀態記憶序列信息，采用3 個門（輸入門、遺忘門和輸出門）控制當前時刻的輸入對記憶的影響，調節各個單元間的信息流，有選擇地加入新的信息給當前狀態，防止梯度消失和梯度爆炸。LSTM 元胞結構模型如圖1 所示。

首先，當前輸入信息xt與上一時刻隱藏層輸出ht-1通過Sigmoid 函數得到從遺忘門中丟棄的信息ft，表示為：

然后，根據需要更新的信息it與生成備選更新的內容通過輸入門將舊元胞狀態Ct-1更新為新元胞狀態Ct，表示為：

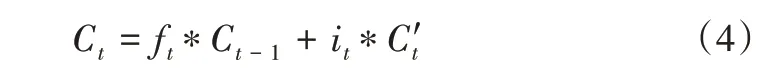
最后，輸入信息xt與上一時刻隱藏層的輸出ht-1，通過Sigmoid 函數得到輸出信息yt，新元胞狀態Ct通過tanh 層與yt相乘得到當前時刻隱藏層的輸出ht，表示為：

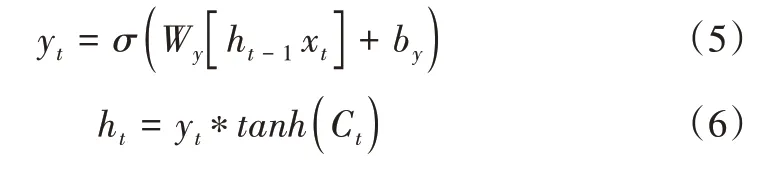
LSTM 目前已出現諸多變種，其中最實用的為門控遞歸單元（Gate Recurrent Unit，GRU），其將控制門的個數減少至2 個，使得模型收斂所需時間有所下降，且與原始LSTM 模型相比幾乎沒有性能損失。

1.2 注意力機制

注意力機制是一種模擬人腦注意力機制的模型［19］，可將其看作是一個組合函數，通過計算注意力的概率分布，以突出某個關鍵輸入對輸出的影響［20］。注意力機制具有高效的信息篩選機制，結合該機制的編碼——解碼（Encod?er-Decoder）框架目前已廣泛應用于自然語言理解、圖像處理等領域［21-22］。

注意力機制通過對模型中不同關注部分賦予不同的權重，從中抽取出重要和關鍵信息，從而優化模型并作出更為準確的判斷［20］。因此，注意力機制對于群體決策有重要作用，并且擁有更好的可解釋性。

Transformer 采用按比例縮放的點積注意力，經過多層感知機（Multilayer Perceptron，MLP）層的向量Q（Query）、K（Key）、V（Value）需要先經過Mask 掩碼操作再進行Softmax歸一化。首先計算Q與K的轉置點積，點積的幾何意義即兩個向量越相似，點積就越大，反之就越小。輸出值即向量的加權和，具體計算公式為：

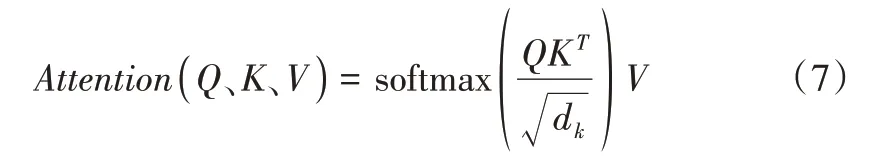
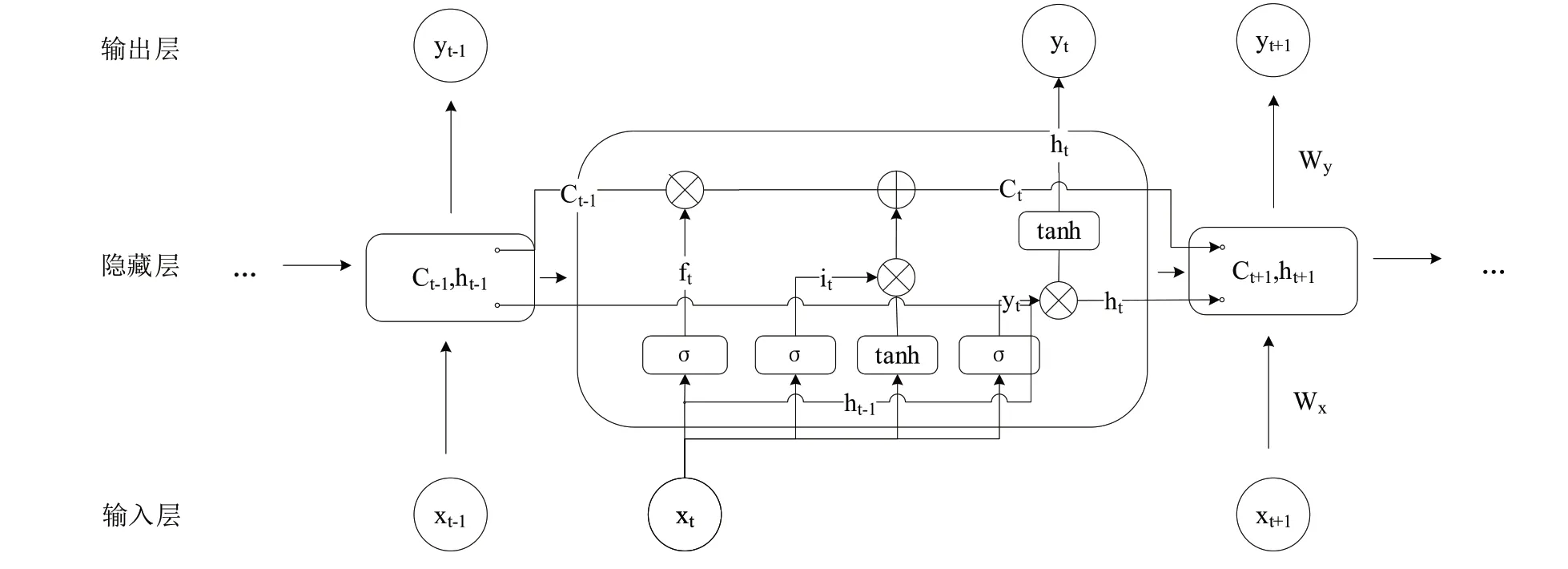
Fig.1 LSTM cellular structure model圖1 LSTM 元胞結構模型

本文借鑒Transformer 模型，配合編碼——解碼網絡，設計出符合魚群運動規律的注意力網絡模型。采用宏觀魚群運動數據訓練模型，并利用該模型計算單體間的注意力數值，表征集群運動中的個體交互作用，從而為微觀交互與宏觀功能之間搭建起可解釋的橋梁。

2 模型建立

2.1 魚群實驗數據提取

采用體型較小且具有集群屬性的紅鼻剪刀魚（Hemi?grammus rhodostomus）作為實驗觀察對象，利用idTracker軟件錄制5 條魚在半徑為25cm 的圓形實驗平臺內集群運動的視頻，并從中提取魚群運動軌跡。

紅鼻剪刀魚具有加速轉向——直線滑行的游泳模式［13］，將其軌跡分解為一系列決策與滑行交替運動的過程，即紅鼻剪刀魚受鄰居魚與環境影響調整運動決策，改變自身朝向并同時加速，緊接著有一個直線滑行的降速過程，以此循環，最終獲得60 312 個決策時刻。

2.2 注意力網絡模型建立

利用決策數據建立注意力模型。首先將智能體決策的輸入觀測變量編碼為高維向量，設計針對魚群運動的注意力層；然后將每個智能體的自身信息與其他鄰居的注意力加權信息聯合，得出單體間的注意力強度；最后使用高斯神經網絡［13］作為解碼器，以模仿單體決策輸出的隨機性，從而構建具有概率輸出的注意力網絡模型。

注意力網絡模型整體架構如圖2 所示，分為解碼器、注意力機制、解碼器3 個部分。采用3 個編碼器對單體的狀態向量進行編碼，構建Transformer 計算注意力所需的3個高維向量：鍵值K、查詢Q 和值V，以進行后續多頭注意力計算。編碼器的輸入狀態包括兩智能體之間的距離dij、焦點單體觀察鄰居的視角ψij、焦點單體與鄰居的航向角差δ?ij。注意力網絡的輸入為編碼信息的集合，因此其輸入層節點個數為編碼器輸出層的兩倍，為使注意力網絡更好地學習到注意力效果，設置兩個隱藏層。

通過考察焦點單體的查詢Qi與鄰居值向量Vj的匹配程度計算焦點單體對鄰居的注意力權重，以確定兩智能體之間的交互強度。由于魚群運動系統的交互作用具有不連續的非對稱性，常用的加性注意力算法以及帶有縮放的點積注意力［19］等均無法應對魚群系統的復雜性。因此，為使單智能體高效跟隨最有影響力的鄰居，注意力權重wij的計算需要先對編碼信息進行組合掩碼操作，并應用SELU激活函數進行非線性處理，以達到良好的集群運動效果，注意力權重的計算公式為：

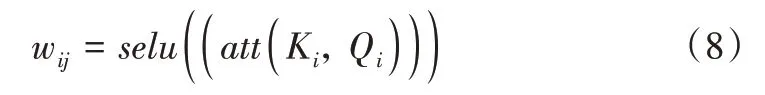
利用注意力權重wij加權平均鄰居值向量Vj，然后聯合焦點單體的值向量Vi獲得解碼器的高維空間狀態輸入oij，表示為：

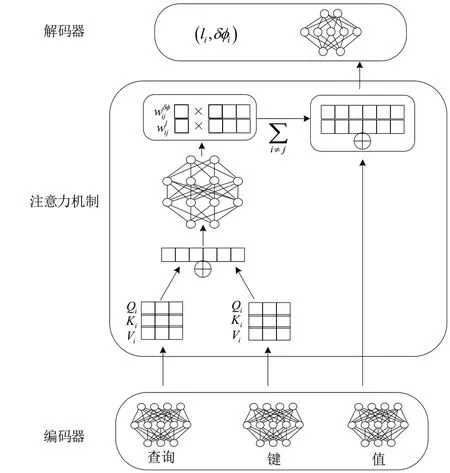
Fig.2 Attention network model overall architecture圖2 注意力網絡模型整體架構

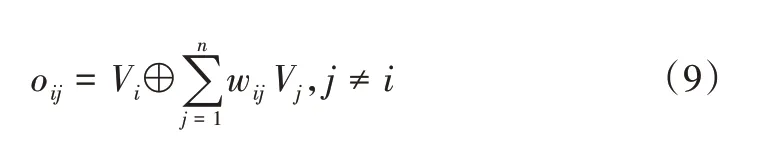
解碼器包含兩個狀態變量信息，分別為焦點智能體直線滑行距離li和航向角度改變δ?i。為實現高斯網絡輸出，輸出值分別為li、δ?i的均值與決策方差。由于魚類群體包含順時針和逆時針兩種相反的運動航向信息，δ?i的處理需要兩倍于li的高斯神經網絡解碼層。注意力網絡模型整體訓練結構如表1所示。

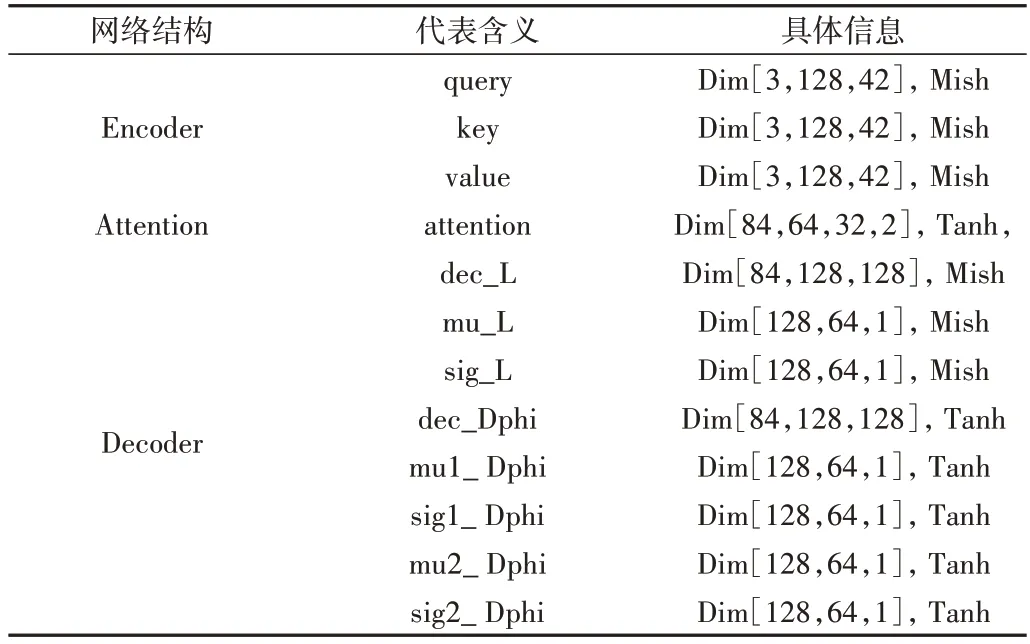
Table 1 Attention network model architecture表1 注意力網絡模型結構

3 實驗方法與結果分析

3.1 模型訓練與超參數設定

采用獲取的60 312 個決策時刻作為實驗數據，進一步處理得到13 494 條實驗數據，其中訓練集包含9 527 條記錄，測試集包含3 967 條記錄。為消除量綱影響，對訓練數據進行歸一化處理。采用PyTorch 深度學習框架編寫網絡模型，訓練程序使用NVIDIA GeForce RTX 3080 GPU 處理器進行加速。設置一次訓練的樣本量（batch size）為1 024，利用Adam 優化器進行訓練，訓練次數為300 輪，學習率為0.000 5。

采用負對數似然（Negative Log-Likelihood，NLL）損失函數之和判定多元高斯分布的均值μ和方差σ的訓練精度，表示為：

3.2 仿真實驗結果

采用5 條魚的實驗數據訓練注意力網絡模型，然后將該實驗數據輸入到訓練后的模型中，比較模型輸出決策與真實魚群實驗決策的概率密度函數（Probability Density Function，PDF）曲線，其中真實魚類單體決策采用實線表示，注意力網絡模型輸出決策采用虛線表示。結果見圖3。

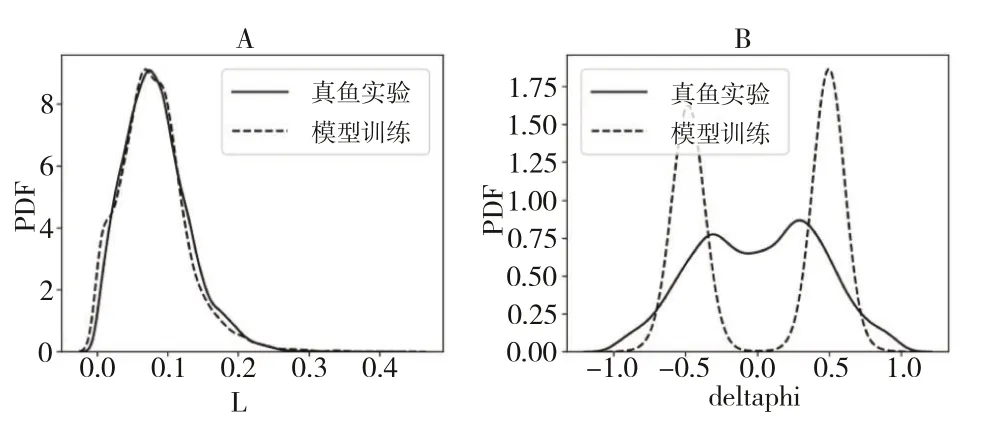
Fig.3 Comparison of gliding distance and heading angle between model training and real fish experiment圖3 模型訓練與真魚實驗滑行距離、航向角改變比較

圖3A 顯示注意力網絡模型訓練的決策距離分布與真魚實驗類似，圖3B 顯示模型輸出的航向角變化決策與訓練數據具有相同的峰值位置，然而曲線明顯陡峭，原因在于模型學習了魚群數據的共性信息，忽略了特性信息，濾除了部分決策隨機性。

為驗證注意力網絡模型應用于集群復雜系統中的有效性，設計了由Python 和LabView 高級語言聯合編寫的多智能體仿真平臺。圖4（彩圖掃OSID 碼可見）仿真結果表明，在1min 內智能體便可以從初始的分散狀態逐漸聚合為穩定的緊湊集群，該瞬態過程也說明了本文模型具有較強的集群聚合特性。

4 結語

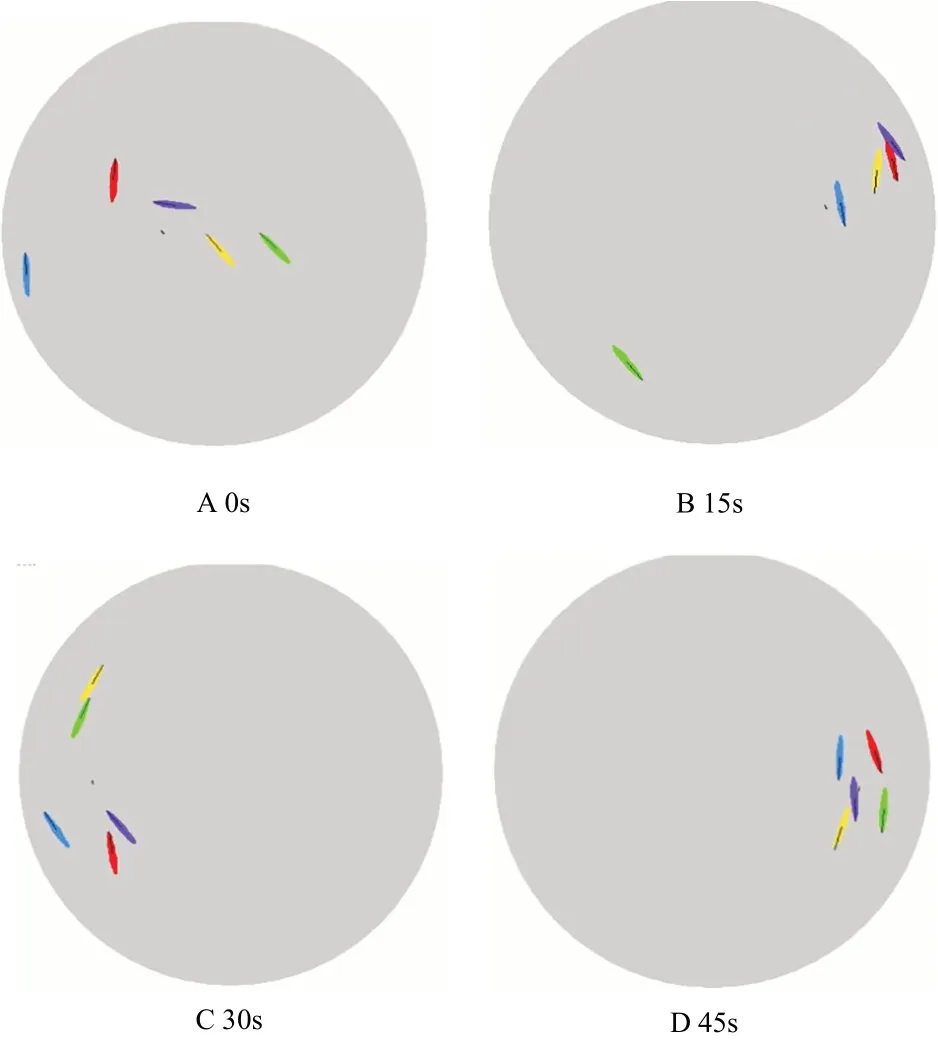
Fig.4 Aggregation process of multi-agent simulation圖4 多智能體運動仿真聚合過程

本文將生物集群行為與注意力機制相結合，提出針對真實魚群運動數據的注意力模型，并將所提模型的仿真效果與真實魚類的滑行距離、航向角變化進行比較。實驗結果表明，本文模型與真實魚類的宏觀運動特性高度一致，可應用于復雜集群系統的研究中。然而，該模型雖然初步實現了多智能體集群運動，但其泛化能力并未展現，下一步將嘗試將該模型運用于大規模智能體仿真實驗中，以實現機器人的智能控制。