基于混料設計對大型曲軸順序鐓鍛工藝參數的優化

孫永剛

（桂林航天工業學院 汽車與交通工程學院，廣西 541004）

0 引言

大型曲軸順序鐓鍛工藝屬于開式模鍛,將坯料加熱到具有一定流動性的塑性狀態,受模具的擠壓運動推動成型,材料的流動狀態很大程度與模具施加給坯料的慣性有很大關系,模腔限制只是在最終合模起決定作用。這種鐓鍛工藝可以保持“金屬纖維”的連續性,力學性能好。但是只有終鍛模具對坯料全部作用,很容易有塌角、折疊、飛邊大等缺陷。傳統的工藝中模具水平運動和豎直運動通過幾何機構聯系起來,成型工藝不靈活,造成廢品率增加,最新的NTR法鍛造機床把豎直運動和水平運動獨立開來,為鍛造更好的曲軸創造了條件。新工藝下曲軸的質量提高了很多,曲軸鍛造成型的評價也增加了一些新的指標,比如,纖維分布,晶粒度,鐓鍛力等多個指標。國內學者也開展多個指標的工藝優化研究,如王棟彥等人對多質量目標的曲軸NTR彎曲鐓鍛成形工藝優化做了分析[1]。各個指標之間相關性,兩種復雜運動的結合在理論上有無限可能性,如何找出最佳的運動工藝參數是非常重要的,這給試驗設計提出了更高的要求。

國內的工程師對大型曲軸的鍛造規律有了更清楚地認識,在趨勢上有了一定的認識,大型全纖維曲軸鐓鍛工藝基本可以分成預彎-預鐓-鐓彎復合-終鐓等四個步驟,而每個工序的模具進給是獨立的,現代鍛壓機床液壓系統完全可以做到,獨立的液壓系統給選擇帶來更大的自由度,同時也帶來更大的難度,但大型設備的鍛造不允許過多的試模,造成大量的浪費。試驗設計和CAE結合是不錯的選擇,CAE基本上不具備試驗成本。實際的鐓鍛機床設有速度及位移傳感器,模具的位置和運行速度可根據工藝需要通過比例流量閥設定并實時控制,水平模具的速度基本上保持固定模式,變化上很少,由機床的機構設計決定。工藝順序尤其是在時間上先后相關聯的工藝試驗設計具有特殊性,這里介紹一種混料試驗設計。

1 混料試驗設計

一般試驗設計中每個因子水平的選擇在固定的定義域內,各個因子之間取值范圍不互相影響,而混料設計是各個因子的分量之和等于1,一個因子的取值直接影響到其他的因子的取值,這是一種受特殊約束的試驗設計,研究方法特殊,常用的包括單純形法、單純形重心法等[2],試驗中變量的約束條件數學表達如下：

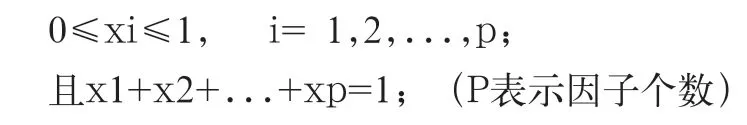
而在生產實踐中很多情形下,響應變量除了與混料分量有關,往往還受到其他變量的影響.在這些非混料分量的變量中,有的是定量的,例如含有過程變量的混料模型；而有的則是定性的[2],這些因素綜合分析起來就是非常復雜的數學問題。所以往往要進行一些簡化,把一些影響結構的分量但不屬于混料分量的量固定下來。那么問題就變得清晰了,如圖1所示,這個模型對應的幾何空間實際上是個3D平面,變量分布應滿足空間立體平面,此平面三個坐標軸的截距為1,在此平面內的變量點滿足約束條件[3]。當變量個數大于3時,就是個超級平面,求解域就是這個平面。針對大型曲軸順序鐓鍛工藝描述如圖2所示,大型曲軸的鐓鍛示意圖,水平運動和豎直運動相互配合后成型,在模具水平和豎直工作的位移滿足曲軸的幾何形狀,這個就是混料分量之和的約束條件。通常情況下彎曲的位移劃分為幾個階段和鐓粗位移相配合,每階段位移工步直接相互影響,符合混料設計試驗的模式。

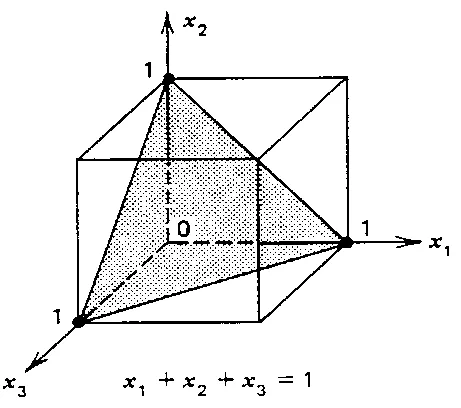
圖1 混圖1料 混設料計設三計變三量變量的的空空間間平平面面

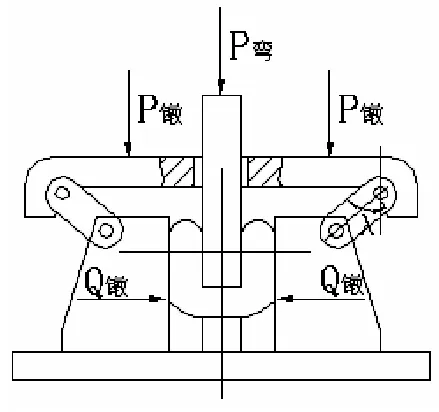
圖2 曲軸鐓鍛示意圖

2 曲軸鐓鍛工藝的混料設計模型的建立

新型大型曲軸的鐓鍛工藝示意如圖2所示,具有開式模鍛的特點,材料在模具的作用下自由流動,曲軸坯料在鐓粗力Q和彎曲力P共同作用下,曲軸由棒料或車好的階梯狀棒料鍛造成最后曲軸曲拐的形狀,鐓粗力Q產生于P鐓粗油缸下行壓力,通過肘桿的幾何放大后使得Q鐓力變大,P彎曲力是成型曲拐部分的作用力,由單獨油缸控制,二者的配合使材料充滿模腔,這種工藝通常稱為NTR法,工藝總結為幾個基本過程包括：預鐓、預彎、鐓彎復合、終鐓所謂“四步”鍛造法[4]。試驗過程需要反復多次試湊,人力物力不允許這樣做,CAE方法具有一定的準確概率,完全可以代替真實的試驗,鐓粗和彎曲兩個方向的運動同時添加速度和力的控制,使得成型達到滿意的目的[5]。盡管如此,CAE仿真的過程中需要制定一定的科學流程才能得到滿意的結果,基本上以成型體積飽滿、表面光整、鐓鍛力合理、再結晶均勻細致等為主要最終目標,這個屬于非常復雜的多目標優化。在仿真之初首先需要找到大概的進給位移量的分布,所以我們在這里的工作就是找到合理的模具位置進給量,而且簡化目標函數為體積成型。

在分析鐓粗和彎曲兩向運動之間的關系時單純用位移量來控制,而具體到鍛壓機床的運動調試過程可以求導數得出運動速度,在驗證模腔充盈度上,對速度細節上忽略。模具水平的控制基本上是肘桿機構聯動,鐓粗動作的力量遠遠超過豎直運動的彎曲鐓鍛力,所以在選擇變量時把彎曲油缸的運動作為混料設計的主要設計變量,換句話說就是用彎曲的運動來適應水平的運動。在空間無限劃分的可能性上有個符合混料設計的基本特征就是彎曲運動的位移為曲軸錯拐量。近似勻速的運動可以將速度分成如圖3的三段,變量的時間域劃分安裝混料設計表制定,縱坐標為位移函數,橫坐標為時間,其中豎直彎曲的位移時間函數為S1（t）,（三因素）：X1、X2、X3,水平模具位移為S2（t）三個階段位移的和是連桿軸頸和主軸頸的距離：X1+X2+X3=105mm（約束條件）。混料設計的基本模型就此完成,分析結果會根據回歸的響應面得出最優的模腔充盈度分段點。

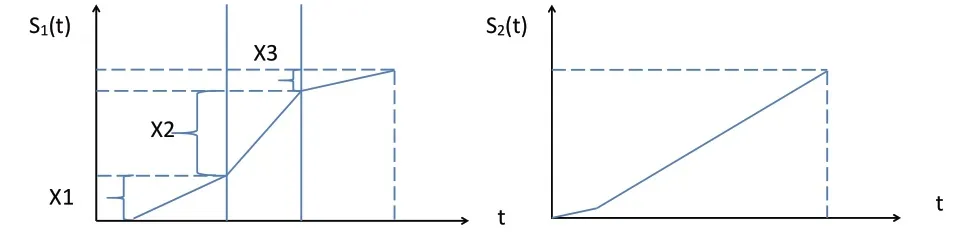
圖3 大型曲軸模具的運動位移規律性曲線（左圖為豎直，右圖為水平）

只考慮彎曲運動,對四段法鐓鍛工藝只參與模具后三段復合運動,預鐓過程不參與,終鐓過程彎曲運動少量參與。從大體成型要求來規定各個變量的范圍,也就是給各變量設定上下界；從試驗設計角度來講,受上下界約束的混料設計的因子空間同普通的混料設計一樣,仍為單形內的一個小單形；而受其它的約束的混料設計的因子空間卻為單形內的一個不規則的凸多面體[2]。在試驗效果上,如果彎曲運動過早,或多或少會出現圖4中平衡塊處塌角的現象,如果出現過晚,會出現圖5中連桿軸頸被撐開過大的現象。

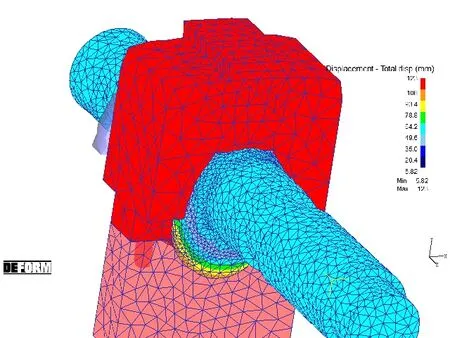
圖4 彎曲過早

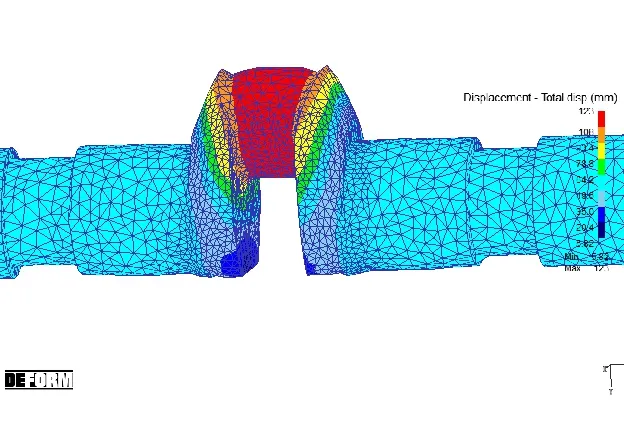
圖5 彎曲過晚

3 混料設計模型及數據處理

單純形格子設計是混料回歸設計方案中最先出現的,也是最基本的設計方案,很多其他設計方案的構成要用到單純形格子設計。標準混合單純形設計表如表1所示,變量為零的試驗方案與事實不符,試驗點大多落在邊界上

在單純混料均勻設計中,介紹均勻設計U7*（74）表變換成UM7*（73）混料均勻表的過程。

比較觀察成型后曲軸的體積,用成型充盈膜腔的程度(SD)來表示響應,用1.0表示最佳,根據CAE結果討論響應度。將表1數據用最小二乘法回歸擬合成 二次多項式：

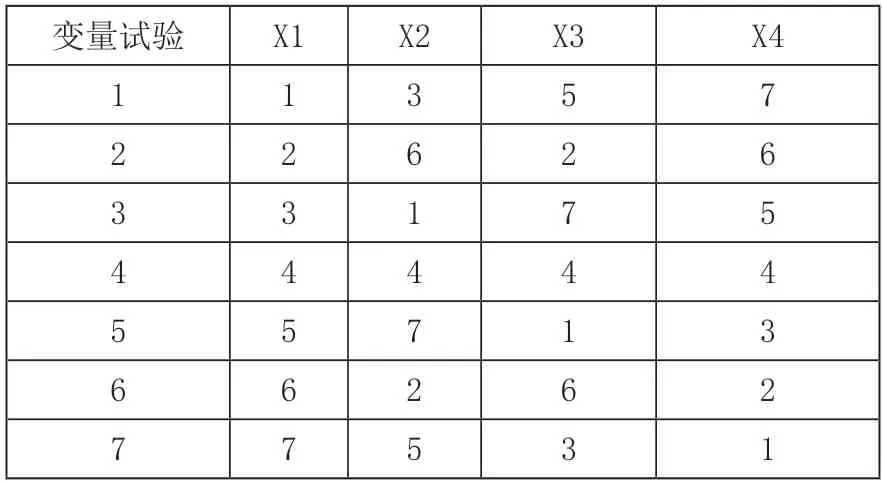
表1 標準混合單純形設計表表1U7＊（74）

SD=+0.75*X1+0.71*X2+0.81*X3-0.070*X1*B-0.66*X2*X3-1.95*X2*X3+11.80*X1*X2*X3；

方程系數方差分析前兩項顯著性一般,將此方程空間二次曲面如圖6所示,根據試驗點沿著響應面上升斜率方向搜索[6],最后找到了一組較為優秀的試驗點,X1=23.5；X2=CAE結果如圖7所示,成型較為理想,對優異參數點的選取上更加集中。

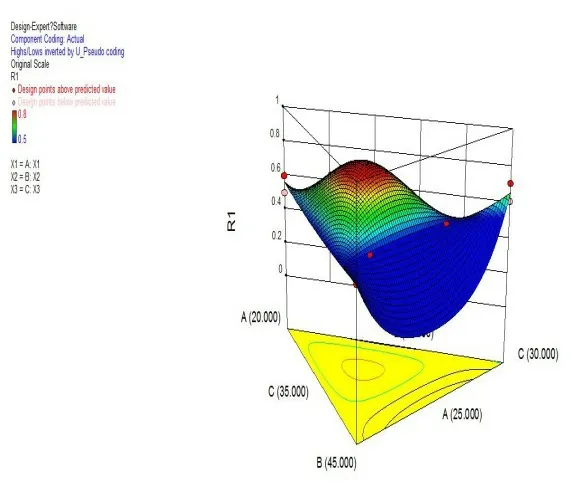
圖6 二次回歸響應面

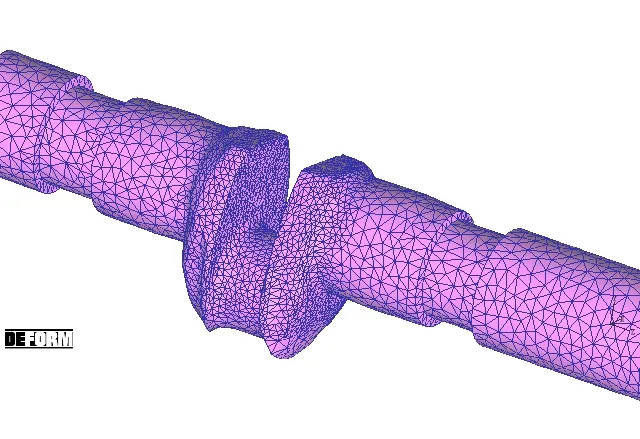
圖7 優化后曲軸成型

4 結語

針對大型鍛件的鍛造參數變化多的情況,通過一系列的CAE數值試驗結合混料設計方法,完成了鍛造參數對成型結果的響應面,并且通過響應面的方向找到了較為理想的鍛造參數,這個模式可以對各種的大型鍛件尤其是成型復雜的鍛件有一定的推廣價值；可以在一定程度上減少試驗次數,而且給出試驗優化的方向,使工程師更加清楚的了解工藝參數對結果的影響,對響應的變量可以選擇更多,復雜程度也可以更進一步,這個繞開了數學和物理方程上的深究,解決問題更簡單化。

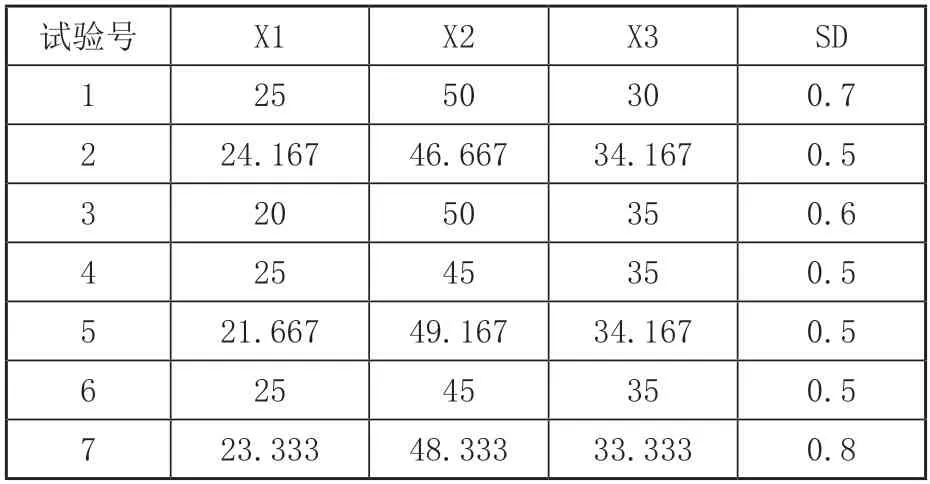
表2 實際混料單純形設計表