基于改進K-means聚類的變壓器開關機械性能自動監測方法

杜 英，王 超，楊 杰，王 倩

（四川省電力公司經濟技術研究院，成都 610000）

0 引言

隨著連入物聯網的設備日趨多元化,物聯網技術對于建設狀態全面感知的智能電網有著至關重要的意義。相關學者在該方面進行了深入研究,周翔等[1]基于混沌理論和K-means算法對通過振動信號對變壓器有載分接開關運行狀態進行監測取得良好的效果；趙莉[2]等采用k-means算法對海量用電數據進行分析,通過對算法進行改進克服其局部最優解的缺陷,快速對用戶用電信息數據進行建模；王子龍等[3]為解決傳統K-means算法初始中心點的選擇隨機性導致模型易陷入局部最優的問題進行改進,提出基于樣本權重改進方法取得良好的效果；王丹丹等[4]為解決重疊目標分割方法不能保留部分輪廓問題,提出采用K-means聚類算法對圖像進行分割,進而提取蘋果目標實現多果重疊目標分割與重建；謝娟英等[5]針對基因數據集區分問題,提出基于統計相關性和K-means的混合基因選擇算法,成功實現對基因子集的區分。

徐雄等[6]為分析水電機組轉輪葉片與轉輪室故障信號特征,采用K-Means聚類算法結合萊特準則對水電機組故障進行預測,檢測準確度得到了大幅提升。張威[7]提出一種基于K-means聚類分析的負荷估計算法,用于估算電網中缺失和未來的測量值,能夠準確的對未來負荷進行估算。

在電力系統中變壓器開關控制器作為配電變壓器智能控制的主要部件,性能會直接影響變壓器工作的穩定性、可靠性和安全性,據國內外統計表明：開關控制器所有引起的變壓器事故占總事故的20%以上,主要為機械故障,嚴重影響電力系統的穩定性。本文設計一種改進K-means算法的電力變壓器開關控制器在線監測系統,構建智能化系統,使其具備智能判斷、自適應調節、故障診斷等能力。

1 變壓器開關振動分析

1.1 相點空間重構技術

機械振動包含著設備狀態、工作模式等大量的設備運行信息,可根據振動信號對設備的運行狀態進行判斷。在變壓器開關切換過程中振動信號會呈現出明顯的強時變、非線性特征,在使用常規方法對其進行分析時不能有效的得出信號中隱含的狀態信息。為解決上述問題,趙彤[8]等根據機械振動的混沌特性,將相點空間重構技術用于對機械正常和故障狀態進行識別,取得良好效果。

相點重構技術通過相互作用的其他分量來判斷當前分量的演化,同時相關分量的信息演化也隱含在當前分量的發展當中,從信號的世界序列數據分析得出所有信號的狀態信息[9]。

假定檢測系統的的一維振動信號為x(i)的時間序列如式(1)所示：

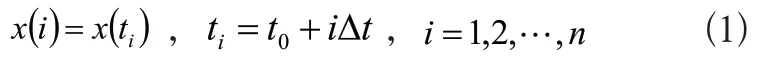
表達式中t0為被測信號的起始時間點的位置；Δt為時間間距；n為時間序列的長度。可將上述公式擴展為p維q個向量,表達式如式(2)所示：

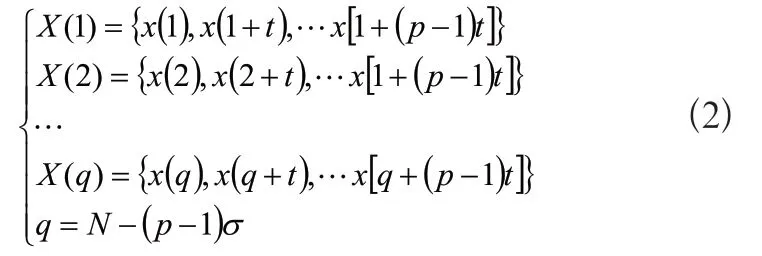
式(2)中：σ為延遲時間,q個向量構成了一個重構信號的相空間。在信號的相空間重構過程中,延遲時間σ刻畫了式(2)中各個坐標分量間的相關性。當σ值過大時,相鄰兩點幾乎不相關,重構的信號彌散；當σ過小時,相鄰兩點相關性較強,重構的信號被壓縮。

通過自相關函數和互信息法等方法確定延遲時間σ主要,通過線性理論進行自相關函數相關度的計算,使用互信息值作為兩個隨機變量間關聯程度的評價依據。根據變壓器開關的振動規律,選取互信息法計算延遲時間。假設振動信號如式(1)所示：

在經歷時間延遲σ后的振動信號如式(2)所示：

此時信號E和R的互信息I(E,R)如式(3)所示：

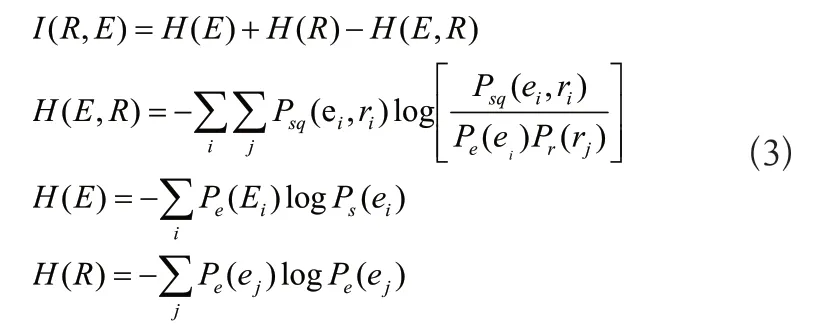
式(3)中：i為離散數值ei的標號,ei和qj為離散數值,j為離散數值rj的標號；Pr(rj)為延遲信號Q中的采樣點的值為rj的概率；Pe(ei)為振動信號E中采樣點值為ei的概率；Per(si,qj)為E中采樣點的值為ei且R中采樣點的值為rj的概率。

不同延遲時間下信號的互信息曲線可通過式(3)計算得到,一般以互信息值曲線中第一個極小值點作為延遲時間。圖1為變壓器開關在切換過程中振動信號的互信息值曲線,當延遲的時間間隔為11時,振動信號互信息值首次出現極小值,取該值作為振動信號的延遲時間。

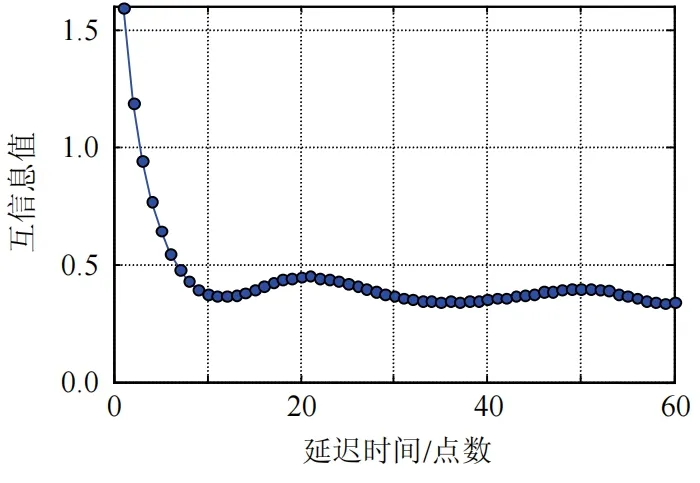
圖1 振動信號互信息值曲線

1.2 算法流程

完成相空間重構后,由高維相空間的相點組成的相軌跡圖替代原有的振動信號,在變壓器開關不同工作狀態下呈現出不同的相軌跡,可從相軌跡圖形中得到開關切換過程中的動力學特性。在傳統K-means聚類分析算法中,初始聚類中心具有隨機性,缺乏自適應性將直接影響結果的準確性。為改善初始聚類隨機性缺陷,通過以下步驟自動確定初始聚類中心和聚類數目：

步驟1：對給出的數據集D,求得其數據集內各樣本的密度β及對應的樣本元素權重θ,將數據集D中密度最大的元素b1作為聚類中心集合B中,得到的集合C=｛b1｝,同時將距離b1點距離小于平均樣本距離的點進行刪除。

步驟2：選擇樣本密度θ與樣本距離乘積最大數值的點,作為第二個初始聚類中心b2,將b2添加到集合B中,得到集合B={b1,b2},將距離與距離b2點距離小于平均樣本距離的點進行刪除。不斷重復上述步驟直到取完所有給出的數據集D,此時集合B=｛b1,b2,...,bk｝,得到具有k個元素的初始聚類,即集合D中的所有樣本點。

步驟3：對給定的數據集D進行K-means聚類運算,將初始聚類中心B作為輸入,直到數據穩定聚類中心穩定,并輸出結果。

改進的K-means算法流程圖如圖2所示。

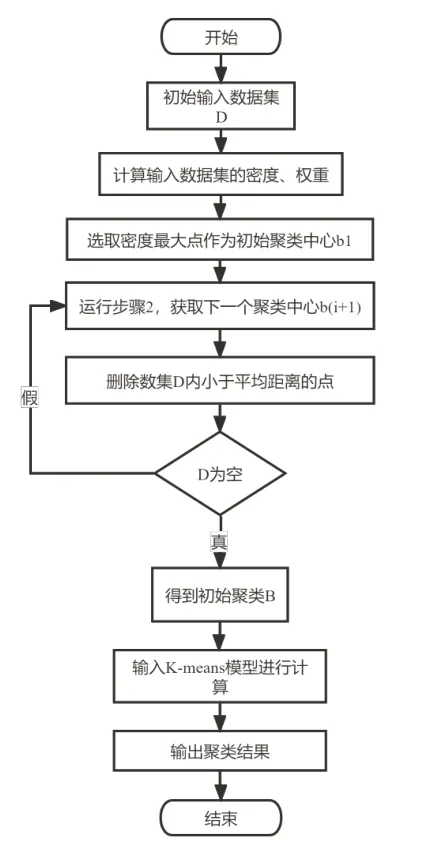
圖2 改進的k-means算法流程

2 仿真數據/試驗設計

2.1 實驗數據及預處理

采用自制的LabVIEW振動測試臺對型號SII-M-220KVA運行過程中的振動信號進行測試,將用于收集振動信號的傳感器分別放置變壓開關兩側,考慮到其沖擊特性和振動信號頻率范圍約為50Hz～50kHz,選擇傳感器采樣頻率為51.2kHz,得到實驗數據如圖3所示。

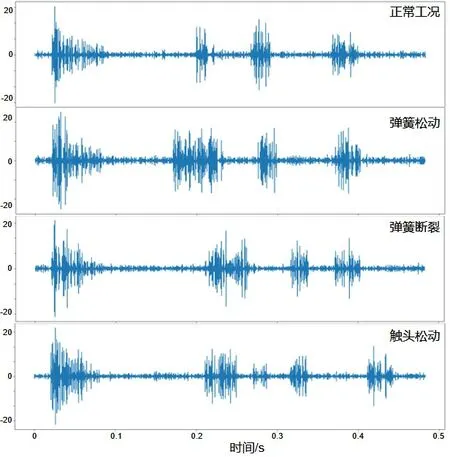
圖3 振動信號圖

在變壓器開關出現斷裂的情況下,信號典型波峰之間的時間間隔會隨之增大,同時振動幅值出現下降；當開關出現主觸頭松動故障時,信號波峰對應的時間間隔出現與開關出現斷裂時不同,可見振動信號的形態與開關的運行狀態有明顯的相關性,截取不同故障出現時間段的振動信號,采用K-means方法對振動信號進行分析。

本次試驗環境采用的是：Intel?Corei9-12900k、16GB內存、GTX3080顯卡、Windows10操作系統、MatlabR2016a。為方便數據的順利的輸入避免測試過程中的噪點干擾,保證實驗結果的正確性,對得到的振動信號數據先進行預處理,去掉局部離散點,同時對數據進行歸一化處理,計算過程如式(4)所示：

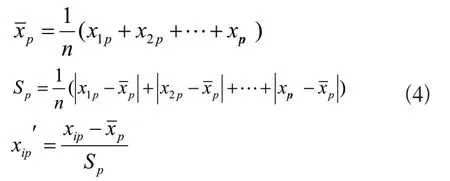
2.2 試驗結果分析

采用準確度ACR、分割系數PC、劃分熵系數PE作為對k-means算法優劣的指標,各指標具體計算公式如式(5)～式(7)所示：

準確度ACR：

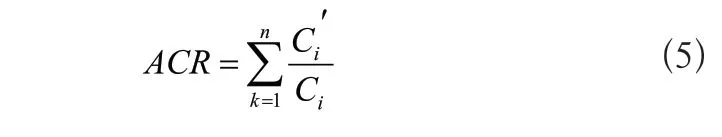
分割系數PC：

分割系數PC的取值范圍在[1/m,1]之間,其值越接近于上限表明結果聚類效果較好,其結果越靠近1/m,表明結果模糊,聚類效果較差。

劃分熵系數PE：

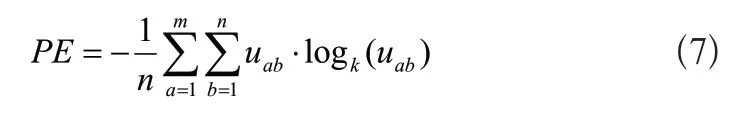
PE取值區間為[0,logkm],其值越接近下限表明聚類效果越好,當其數值越接近logkm時,表明聚類效果較差。

本次實驗采用WK-means算法、ZKmeans算法、DCK-means算法、經典K-means算法和本文方案進行對比分析,將每種算法對數據集D進行計算,結果取平均值,表1為5種方案測試結果。

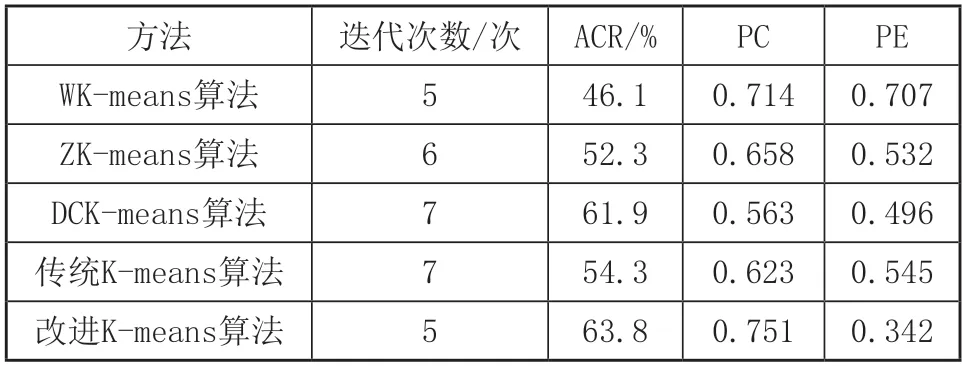
表1 各方案對比分析

準確度方面改進K-means算法比WK-means算法高出17.7%,較ZKmeans算法準確度高出11.5%,比DCKmeans算法高1.9%,與傳統K-means算法相比準確度高9.5%,改進后k-means準確度明顯提高。在迭代速度方面,改進K-means算法的迭代次數與初始聚類中心的選擇有著較大的聯系,迭代次數與DCK-means算法一致都為5次,DCK-means算法在尋找初始點考慮了距離和密度因素,與其他算法相比更具全局性,故迭代次數較少,本文采用的改進K-means算法在初始聚類中心的尋找過程中引入平均樣本距離和樣本密度,結合了數據集局部與宏觀特征,減少了異常因素的影響使樣本距離的度量更準確,得到的初始聚類中心分布更為合理,迭代次數與傳統K-means算法相比明顯降低,有利于減少運行時間。

分割系數PC其值越接近于上限1,表明算法擬合效果越好,改進K-means算法取得0.751,與傳統算法相比大幅提高20.4%,同時也高于其他三種算法。劃分熵系數PE數值越接近下限,表明算法的擬合效果越好,改進K-means算法取得0.342,與傳統K-means算法相比大幅下降37.2%,小于其他對比算法。綜合準確度ACR、分割系數PC、劃分熵系數PE來看,改進K-means聚類算法的擬合校核和迭代次數都得到了明顯提高,

3 結語

為對變壓器開關的工作狀態進行實現實時監控,通過對傳統的K-means聚類算法進行改進,建立基于振動信號的故障診斷方法。在K-means聚類算法選取初始聚類中心的過程中,通過結合樣本密度、元素權重和樣本距離等因素,改善了傳統算法易陷入局部最優解的缺陷。為驗證改進后算法的準確性,采用自制的LabVIEW振動測試臺對模擬變壓器開關振動,分別采用WK-means算法、ZKmeans算法等進行對比分析,從綜合準確度ACR、分割系數PC、劃分熵系數PE方面對不同算法進行對比分析,結果表面改進后K-means算法擬合效果明顯優于對比算法,為變壓器開關故障檢測提供了一種新的思路。