基于張量的方法及應用綜述

夏 虹，張雅倩，靳曉東，陳彥萍，高 聰，王忠民

(1.西安郵電大學 計算機學院，陜西 西安 710121；2.西安郵電大學 陜西省網絡數據分析與智能處理重點實驗室，陜西 西安 710121)

0 引 言

傳感設備和移動互聯設備的普遍應用使得其產生的數據量飛快增長，關系錯綜復雜[1]。類型的多樣化和結構的復雜化導致挖掘數據背后隱藏的信息變得困難，亟需引入一種高效的融合模型對這些多源異構數據進行統一表示。現有的數據融合統一表示方法有本體論、語義網、大圖模型等，這些方法雖然在很多領域已經有了廣泛的應用，但其表示形式較為簡單，難以對高維空間中的跨領域異構數據進行表示。因此，基于張量的異構數據統一表示方法開始被研究人員關注[2]。作為向量和矩陣向高階的擴展，張量可以保持復雜數據的潛在結構，能夠很好的描述和表示高維度、多樣化的海量數據。

數據的高維特征使計算處理的時間和空間復雜度急劇增加，隨之帶來的是“維度災難”問題，所以在應用之前如何對這些高維數據進行降維處理是一個重要環節。已有的縮減維數的方法有相關系數矩陣、獨立成分分析、主成分分析、線性判別分析等，這些方法有一定的降維效果，但是會不可避免的破壞原始數據的內在結構，造成一定的損失。基于張量對高維數據強大的表示能力，一些工作[3-6]引入張量分解來獲取這些數據的低維特征，在降低計算復雜度的同時還可以維持原有數據的幾何結構，減少損失。

由于各種不可避免的因素，如錯誤操作、缺少權限等，在實際應用中獲取到的多維數據集往往是不完整的，如何利用已獲得的數據來估計缺失值是張量補全所要解決的問題。雖然矩陣補全[7-8]在過去的幾十年已經得到廣泛的研究，含缺失值的張量也可以被展開為矩陣從而通過矩陣補全方法進行恢復。但是這些方法會破壞張量的多維內在結構，并且當引入更高維的大數據時會帶來指數級增長的計算復雜度，無法進行高效的數據修補，因此需要利用張量全局結構中的多維信息來補全缺失值。

近年來，張量研究在數據挖掘、圖像處理、服務質量預測、交通流量預測等領域得到廣泛的關注。基于以上對張量分解和補全問題的簡單介紹，下文主要對相關方法及應用進行總結，為同行研究人員提供一個參考，以促進未來的工作和應用。

1 張量分解方法

最先提出的張量分解方法為CP分解和Tucker分解，它們將一個N階張量分解為若干因子矩陣來減小存儲空間并挖掘其核心要素。之后為了增強解釋能力并提高計算效率，張量網絡作為對傳統分解方法的推廣被提出，主要包括張量鏈和張量環，思想是將一個高階張量表示為一組稀疏的互相連接的低階張量，從而一個大規模高階張量優化問題可以被轉化為小規模低階張量的處理問題，從而能夠減輕維度災難的影響。本節介紹CP分解、Tucker分解、張量鏈分解以及張量環分解的過程及各自的優缺點。

1.1 CP分解

CP分解[9]將高階張量表示為有限個秩為1的張量之和。三階張量的CP分解過程如圖1所示。對于一個N階張量，CP分解可表示為：

χ≈[λ;A(1),A(2),…,A(N)]≡

(1)

其中，°表示向量外積，R是張量的秩且分解后的因子矩陣A(n)∈RIn×R(n=1,2,…,N)。

圖1 三階張量χ∈RI1×I2×I3的CP分解過程

除了排列以及縮放的不確定性外，CP分解僅存在唯一可能的秩1張量的組合，數學表達形式簡單，分解過程簡便，可以大規模處理分布式數據集，但張量秩R的定義對分解結果影響較大，很難找到最優解。

1.2 Tucker分解

Tucker分解[10]是將高階張量表示為一個核心張量和若干個張量模對應的伴隨矩陣的乘積。三階張量Tucker分解過程如圖2所示。一個N階張量的Tucker分解表示為：

χ≈[G;A(1),A(2),…,A(N)]=

G×1A(1)×2A(2)…×NA(N)

(2)

其中,核心張量G包含原張量中的主要信息，分解得到的每個因子矩陣A(n)(n=1,2,…,N)表示第n階上的主成分。

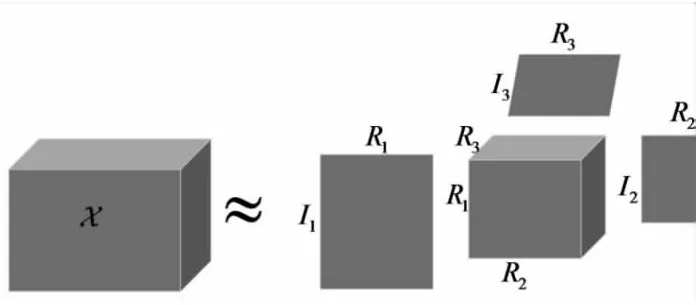
圖2 三階張量χ∈RI1×I2×I3Tucker分解過程

分析以上兩種分解過程可以明顯看出，CP分解是Tucker分解的一種特殊情況，即當Tucker分解中的核心張量G是對角的且每一階對應的維數相等時，它也就變成了CP分解。與CP分解方法相比，Tucker分解更容易捕獲目標張量中的潛在聯系，得到的核心張量的存儲空間相對于原始張量會大大減小，但其參數的數量與張量階成指數關系，時間復雜度與核心張量大小密切相關，因此不適合大規模數據的處理。

1.3 張量鏈分解

對于張量鏈分解(TT分解)[11]，其主要思想是使用張量的縮并運算將一連串稀疏的低階張量(大多是2階或3階)進行互連來表示一個高階張量，張量核的個數與張量的階數保持一致。圖3是一個N階張量的張量鏈分解過程，其數學表達式為：

χ=X(1)·X(2)·…·X(n)·…·X(N)

(3)

其中，·表示張量的縮并，即張量的單模乘。{r0,r1,…,rN}代表張量鏈的秩，且r0=rN=1。X(n)∈Rrn-1×In×rn(n=1,2,…,N)稱為核心張量(或張量核)。張量鏈中的元素定義為χ(i1,i2,…,iN)=X(1)(:,i1,:)X(2)(:,i2,:)…X(N)(:,iN,:)。

圖3 N階張量χ∈RI1×…×IN張量鏈分解過程

TT分解的原理是通過矩陣的序列乘積來近似張量中的每個元素，其中第一個和最后一個矩陣是向量，以確保標量輸出。所以TT分解完全基于矩陣的QR或SVD分解序列，在處理一個高階張量時是穩定的，且不需要進行任何遞歸操作，分解后的參數級別和CP分解相同，所以它能夠解決維度災難的問題。但是TT分解會受到以下幾點限制：(1)TT秩的限制，即r0=rN=1導致了有限的表示能力和靈活性。(2)TT秩總是有一個固定的模式，即邊界核越小，中間核越大，這不是特定張量的最佳模式。(3)張量核的多線性乘積有嚴格的順序約束，這使得優化的張量核高度依賴于張量維數的排列，但尋找最優排列是一個較為困難的問題。

1.4 張量環分解

一些學者考慮解決上述張量鏈分解的局限性。首先，需要針對TT秩的限制即r0=rN=1放寬條件，從而提高數據的表示能力。其次，應減輕多線性乘積在張量核之間受排列順序的影響。第三，通過使模型對稱實現對張量核的循環移位和等價處理。為此，文獻[12]發現這些目標可以通過使用跡操作來實現。由于這些張量核是循環互連的，看起來像一個環結構，所以這種分解模式被稱為是張量環分解(TR分解)。

TR分解將一個高階張量表示為一連串循環相乘的三階張量。N階張量的張量環分解過程如圖4所示。其數學表達式為：

χ=tr(X(1),X(2),…,X(n),…,X(N))

(4)

其中與TT分解類似，X(n)∈Rrn-1×In×rn稱為核心張量，{r0,r1,…,rN}表示張量的秩，不同之處在于TR分解的秩約束為r0=rN，而不需要為1。張量環中的元素可以定義為χ(i1,i2,…,iN)=tr(X(1)(:,i1,:)X(2)(:,i2,:)…X(N)(:,iN,:))。

圖4 N階張量χ∈RI1×…×IN張量環分解過程

TR分解后得到的張量核都是三階張量，表示形式更加統一，存儲的變量數量較少，其分解格式是張量對張量的分解，因此它可以更好地保持原始數據的內在結構。TR分解的特點在于每個張量核在跡操作下都可以進行循環移位和等價處理，而其他分解方式未能保持這一優勢。

2 張量補全方法

在采集數據的過程中，一些無法避免的外在條件的干擾導致獲取的數據往往是不完整的。張量補全用來填補缺失的或未觀測到的條目。重構張量分解后的低秩因子也可進行張量補全，但是張量分解目的是從高維數據中提取出一個低秩結構來降低計算復雜度，而張量補全是利用獲取到的低秩模型來估計缺失的數據。兩者目的的不同限制了一些傳統的分解方法的應用，需要對其進行改進，并且這些方法需要手工設置張量秩。張量補全需要明確目標張量中哪些數據是已觀測到的，在每次迭代過程中都需要估計丟失的信息。除了基于分解的方法外，Liu[13]在矩陣跡范數的基礎上對張量跡范數進行定義，將張量秩最小化問題表述為凸優化問題，提出了幾種低秩張量補全模型。雖然這些展開矩陣由于具有多線性相關性而不能獨立優化，但這些方法可以在預先不設置張量秩的情況下來解決張量補全問題，減輕自定義張量秩的影響，這在實際操作中更易于處理。本節對幾種基于分解的和基于跡范數的補全方法進行介紹。

2.1 基于分解的方法

基于分解的方法根據已觀測到的條目將目標函數定義為最小化原始張量與分解重構之間的誤差，然后通過對目標函數進行多次迭代優化得到理想的潛在因子，利用這些潛在因素來預測缺失條目。下面列舉幾種基于分解的方法需要優化的問題。

CP分解需要優化的問題如下：

(5)

其中，χ和S是每個維度具有相同大小的n-模張量，在集合Ω中的元素是已給定的。

Tucker分解需要優化的問題如下：

(6)

張量鏈分解需要優化的問題如下：

(7)

張量環分解需要優化的問題如下：

(8)

對以上幾種優化問題的求解可以分為兩種情況。第一種情況是缺失值的輸入和模型參數的交叉估計同時完成，通常使用交替投影優化來解決，如ALS優化。這種方法操作簡單，但如果缺失比率逐漸增加，收斂速度可能會降低。第二種情況是忽略缺失值，只根據觀測到的部分數據來建立模型，通常使用梯度優化或概率方法來求解，對以上幾個目標函數進行加權優化，在缺失率較高時有很好的補全效果。

2.2 基于跡范數的方法

基于跡范數最小化的方法被稱為低秩張量補全，是低秩矩陣補全的推廣，定義了張量跡范數，并將基于張量的非凸秩最小化問題定義為凸張量跡范數極小化問題。下面介紹基于跡范數的補全方法需優化的問題及相應求解算法。

基于秩最小化的張量補全模型需要優化的問題如下：

(9)

(10)

本質上，張量跡范數是沿所有模態展開所得的矩陣跡范數的凸組合。

Liu等人在文獻[13]中提出了幾種解決上述跡范數最小化問題的算法。2.2.1和2.2.2節分別介紹了簡單低秩張量補全算法和高精度低秩張量補全算法及各自的優缺點。

2.2.1 簡單低秩張量補全

引入n個輔助矩陣M1,M2,…,Mn，可以將優化問題轉化如下：

(11)

由于χ(i)=Mi的約束限制，矩陣跡范數項依然相互依賴難以解決。下式通過引入懲罰項βi(i=1,2,…,n)來獨立地解決每個子問題。

(12)

這是一個凸但不可微的優化問題，能夠使用塊坐標下降法來解決，在優化其中一個塊變量的同時對其余塊變量進行固定，因此將問題(12)轉化為對χ,M1,M2,…,Mn共n+1個塊的優化求解。

在其余n個塊變量都固定的情況下，通過優化求解問題(13)來得到最優χ。

(13)

此問題的最優解如下：

(14)

簡單低秩張量補全算法分割矩陣跡范數項之間的依賴關系，使它們能夠獨立求解，并通過使用塊坐標下降法尋找全局最優解。雖然該算法較易實現，但在實際操作過程中收斂速度較慢，并且擴展到一般張量跡范數最小化問題也很困難，不具備通用性。

2.2.2 高精度低秩張量補全

(15)

上式對應的拉格朗日函數如下：

(16)

由于交替方向乘子法(ADMM)能夠有效解決大規模目標函數中含多個非光滑項的優化問題，因此被用來求解函數(16)的極值。

更新χ需要求解以下優化問題：

(17)

最優χ可表示如下：

(18)

高精度低秩張量補全算法旨在解決沒有觀測噪聲的張量補全問題，使用ADMM方法直接處理等式約束，而不采用任何松弛技術，可以更快地實現較高的補全精度。

3 張量分解的應用

目前各個領域所產生的數據規模逐漸變大，呈現出高維的特征。直接操作這些高維數據會導致計算復雜度急劇增加，并且可能出現“維度災難”的問題。根據第1節中幾種方法的分析，張量分解的目的是對高維數據進行降維處理和特征提取，解決傳統降維方法會破壞內在信息和結構的缺陷。第1節介紹的分解方法及推廣目前被應用于很多領域，本節主要介紹張量分解方法在多源異構大數據分析[3,4,14]、人臉識別[5,15-16]和數據壓縮[6,17-19]這三種應用場景的最新進展。

3.1 多源異構大數據分析

日漸豐富的傳感設備及移動互聯設備從多個維度進行數據的采集，得到海量的多源異構數據。在數據量快速增長的時代，如何對海量、多源、異構數據進行統一表示以及降維處理是亟需解決的問題。目前基于本體論、語義網、大圖模型的表示方法僅在一定領域有好的效果，但不能在多數場景中通用，并且由于數據的高維性會丟失部分特征。為了減少存儲空間及后續的計算成本，解決“維度災難”問題，還需要對這些統一表示后的高維數據進行降維處理以獲取高質量的核心數據。傳統的主成分分析、因子分析、獨立成分分析等方法僅適合處理低維數據，在高維數據處理方面效果不佳并會損壞內部結構，并且不能有效處理增量產生的流式數據。張量模型由于具有良好的統一表示能力和降維效果而在多源異構大數據分析中受到關注。

Kuang[3]首先提出把從多個維度采集到的復雜異構數據使用張量模型進行統一表示，為結構化、半結構化和非結構化數據分別建立子張量，然后利用張量擴展算子進行融合。王在文獻[4]中提出了多種基于雅可比正交化的分布式增量高階奇異值分解方法，包括單模分解方法、樹形多模分解方法、基于RoundRobin環的分解方法以及嵌入式樹形多模分解方法。這些方法用來解決分布式以及增量處理中的張量展開問題。文獻[14]還將張量鏈分解引入大數據增量式降維問題中，分別介紹了基于奇異值分解和QR分解的增量式張量鏈分解方案，僅存儲更新后得到的低階核心張量來減小存儲空間并提高處理效率。

3.2 人臉識別

目前，在人們的日常生產生活中越來越多的用到人臉識別技術，如智能門禁、員工打卡、移動支付等。所以人臉識別研究在很多領域變得流行，并且現在已經取得了一些顯著成果。人臉圖像信息通常以高維的形式呈現，如何從這些高維數據中進行特征提取是人臉識別中的一個關鍵環節。傳統的基于向量的人臉識別方法如LDA、PCA、LPP以及基于矩陣的人臉識別方法如2D-LDA、2D-PCA、2D-LPP等會破壞人臉圖像原有的幾何結構，并在降維的過程中會造成信息損失，所以一些研究人員考慮使用張量來建模人臉的彩色圖像信息，并基于張量分解方法來減小原始人臉圖像的維度數。

由于人臉圖像中的數據都是非負的，梁[5]在非負矩陣分解方法的基礎上提出了基于非負張量分解的人臉識別方法，能夠很好地捕獲人臉內部核心信息，識別效率比NMF或PCA要高。宋等人[15]為了解決非負張量分解在提取人臉特征時冗余信息太多以及表達形式不夠簡單的問題，在此基礎上添加正交稀疏約束來獲得相關性較低的基圖像從而能夠獲得較好的識別效果。為了避免圖像增加時的重復運算，文獻[16]提出了一種基于隨機增量張量奇異值分解的識別算法，將隨機張量模型與張量奇異值分解方法相結合，可以在已有的隨機奇異值分解結果的基礎上來進行下一步的更新運算。

3.3 數據壓縮

各個領域所產生數據的急劇增多帶來的是如何進行有效存儲和傳輸的問題，數據壓縮技術被用來去除原始大規模數據中的冗余信息，在基本不損失核心信息的情況下來減少數據量或者重新組織數據從而提高處理以及存儲效率。目前需要處理的數據大都存在著天然的高維結構，傳統的基于向量或矩陣的模型難以描述這些高維數據的空間結構和相關性，一些研究提出基于張量模型的方法來解決數據壓縮問題，降低時間和空間復雜性，提升壓縮性能。

在視頻圖像壓縮研究中，李[6]將視頻數據用張量模型進行表示，并使用張量迭代Tucker-ALS算法來減少原有視頻數據的維數，取得了很好的壓縮效果。針對配電網大數據的壓縮研究，趙[17]為了保持高維數據的空間結構并解決海量異構配電網數據的存儲問題，利用張量模型對智能配電網異構數據進行統一表示并提出了基于Tucker分解的多維配電網數據壓縮方法。在此基礎上，趙[18]還利用配電系統中數據量大且隨時間積累的特點，提出了一種基于增量張量分解的配電網流數據壓縮方法，使用實時新增數據來更新歷史壓縮結果。在高光譜圖像的壓縮問題中，Li[19]考慮高光譜圖像不同維度之間的關聯，提出了一種基于相關的Tucker分解方法來分別構造核心張量和因子矩陣，可以被應用于任何基于Tucker分解的n階張量中，壓縮性能得到提升。

4 張量補全的應用

在獲取高維復雜數據的過程中，由于各種不可預測的情況，如錯誤操作、缺少權限等，其中某些元素會丟失，影響后續應用。所以如何捕獲已有元素和缺失元素之間的潛在聯系，利用已獲取的數據預測缺失值成為一個亟需解決的問題。第2節介紹的張量補全及改進方法已被應用到很多領域的缺失值處理中。本節基于QoS缺失數據預測[20-23]、短時交通流量預測[24-27]、圖像恢復[28-31]三個應用場景對張量補全進展進行探討。

4.1 QoS缺失數據預測

服務數量的急劇增多使得用戶在過去只能調用有限的服務并獲取對應的QoS值。但依據稀疏的QoS數據很難進行準確的服務推薦或組合，所以QoS缺失值預測是進行服務相關操作的重要環節。基于矩陣分解的QoS預測方法已經取得很好的效果，但其只用到用戶和服務的二維信息，預測效果受限。在動態的互聯網環境下，受服務器負載限制、網絡狀態波動、用戶移動性需求等因素的影響，時間、位置和一些其它因素會導致QoS值發生變化，所以需要盡可能利用多維數據來預測未知QoS值。一些研究工作使用張量模型對高維QoS數據建模以考慮多個維度的信息來提高預測精度。

為了捕獲隱藏在時間模式下的潛在信息，Zhang[20]首先將基于用戶和服務的靜態矩陣模型擴展到三維的用戶-服務-時間動態張量模型，并考慮QoS數據的非負性，使用非負CP分解算法來處理模型中的三元關系。除了CP分解，Zhang[21]還將Tucker分解應用于QoS缺失數據預測問題，為了應對QoS數據流動態傳入所帶來的挑戰，還引入了一種基于奇異值分解的增量張量分解方法來減少存儲空間并提高計算效率。文獻[22]根據用戶和服務的位置將已有的QoS數據分別建模為局部和全局三階張量，將位置聚類和分層張量分解相結合來實現QoS預測，該方法能有效提高預測精度并緩解數據稀疏性問題。上述只針對某一個維度進行預測，而沒有考慮多維度(位置、時間等)之間的相關性，馬[23]利用張量對多維度的QoS數據進行建模，通過高效求解張量分解優化算法來實現好的預測效果。

4.2 短時交通流量預測

為了緩解城市中的交通擁堵的問題，幫助出行者更好地選擇出行線路，節省時間，短時交通流量預測是智能交通系統中一項重要的任務。已有的方法考慮交通數據的時間變化特性、空間相似性以及周期性進行預測，但這些方法大多基于向量或矩陣形式，數據維度的約束導致難以同時描述交通數據多模式之間的潛在聯系，預測效果會受到一定的限制。所以張量開始被引入到短時交通流量預測問題中來封裝交通流量數據。文獻[32]將采集到的交通數據構建為天-小時-時間三階張量的形式，在對丟失的交通數據進行補全時，獲得了比向量和矩陣模型更好的效果。但在短時交通流量預測問題中，對未來數據的預測需要用到實時獲得的數據，并隨時間的推動來選擇預測區間，靜態交通數據補全方法難以描述交通數據的動態變化情況，所以研究者往往將交通數據構建為動態張量形式，不僅保留了原始數據的多模式關系，還能體現交通流的動態特征。

段[24]根據交通數據的多模式特征構建Time×Day×Week×Location四階張量，并引入滑動窗口來選取固定長度的張量流作為歷史數據，介紹了基于CP和Tucker分解的動態短時交通流量預測方法。除了基于這兩種分解方式的預測方法之外，耦合張量分解也被應用到短時交通流量預測問題中。Zhou等人[25]選取交通流數據和平均車速數據分別構造兩個張量并以“路段”模式耦合，提出了一種基于矩陣和張量的加權優化算法來恢復交通流量數據，這是第一次為交通數據處理應用引入一個新的代數框架，不同于傳統的單張量模型。為了進一步改進預測效果，文獻[26]提出了一種基于快速低秩張量補全的增量啟發式交通流量預測方法，該模型將增量張量結構與快速低秩張量補全相結合，集成了交通流數據日、周、時間、空間等多模式的特征。Li等人[27]探討了在各種常見的缺失場景以及不同的缺失率下幾種經典的張量補全算法是否以及如何影響最終的預測精度，這是第一篇分析丟失數據及其補全對交通流預測的詳細影響的論文。

4.3 圖像恢復

實際應用中的圖像大多都存在高維特征，如高光譜圖像、醫療圖像、視頻等，這些多維圖像中包含著比傳統二維圖像更加豐富的信息，但在生成、存儲與傳輸的過程中會受到很多外界條件的影響而不能準確處理后續應用，對這些高維圖像的處理問題大多是根據已觀測到的數據來進行高質量的圖像填充，將其還原到原來的真實圖像結構。目前基于矩陣補全的方法要求圖像行列之間有高度相關性，并且在展開為向量之后會破壞圖像的內部結構，所以一些研究將張量補全方法應用于圖像恢復問題中。

在高光譜圖像超分辨率研究中，由于需要將低空間分辨率的高光譜圖像和高空間分辨率的多光譜圖像進行融合來捕獲兩者互補的因素，耦合張量分解方法常被應用至該問題的研究中。Xu[28]提出了一種基于耦合CP分解的方法來探討高光譜和多光譜圖像之間的關系。Xu還使用耦合張量環分解來探討圖像的非局部自相關性和全局譜相關性，將兩類圖像融合表示為耦合張量環模型從而共享其中的潛在核張量之間的關系[29]。在醫療圖像處理方面，文獻[30]針對僅使用單一秩來解決動態MRI重建問題的缺陷，考慮同時最小化CP和Tucker秩來更好地利用動態MRI數據低秩分量的相關性。Cui等人[31]將基于分層概率模型的CP分解方法用于EEG缺失數據的恢復問題中，張量秩能夠被自動確定，而不用手工賦值。

5 存在問題與挑戰

雖然張量分解及補全方法在很多領域已經取得了很好的成果，但在復雜的應用場景下還存在一些問題與挑戰需要進行深入的研究。(1)大多數已有的張量分解算法都是在單機模式下運行的，但隨著大數據時代的發展，傳統單機模式已經無法應對復雜的海量數據，為了提高計算效率并保持分解精度，可以將已有的算法擴展到分布式環境下運行。(2)如何進一步提高張量分解的降維效率和張量補全的預測精度并將其應用于不同的場景是需要一直進行探索的。(3)將張量模型與新興領域如邊緣計算、物聯網、車聯網或者新興技術如深度學習、神經網絡等相結合來高效解決更多的問題也具有重要意義。相信在之后的研究發展中張量分解及補全相關算法會有更大的發展前景，能夠在最大程度上發揮張量模型的應用價值。

6 結束語

張量模型具有對高維數據強大的表示和處理能力，該文總結了張量分解及補全中的幾種經典方法，其中張量分解方法包括CP分解、Tucker分解、張量鏈分解以及張量環分解，分析這些方法的基本思想及優缺點。張量補全方法從基于分解和基于跡范數兩方面進行介紹，基于分解的方法利用張量分解得到的低秩結構來估計缺失值，基于跡范數的方法需要解決跡范數最小化的優化問題。接著從多源異構大數據分析、人臉識別、數據壓縮三方面來總結張量分解的最新應用。針對QoS缺失數據預測、短時交通流量預測、圖像恢復三個場景來介紹張量補全的最新算法。最后對張量分解及補全方法研究中存在的問題與挑戰進行展望。