Efficient quantum private comparison protocol utilizing single photons and rotational encryption

Tian-Yi Kou(寇天翊) Bi-Chen Che(車碧琛) Zhao Dou(竇釗) Xiu-Bo Chen(陳秀波)Yu-Ping Lai(賴裕平) and Jian Li(李劍)

1Information Security Center,State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

2Information Security Center,School of Cyberspace Security,Beijing University of Posts and Telecommunications,Beijing 100876,China

Keywords: quantum private comparison,rotational encryption,polarized single photons,efficiency

1. Introduction

Secure multiparty computation (SMPC) problems are cryptographic tasks that enable joint computation using private input from all parties without revealing them.In the traditional secure two-party computation scenario,Alice,who has secret inputx,and Bob,who has secret inputy,are willing to calculatef(x,y). The origin of SMPC problems can be traced back to Yao’s millionaire problem,[1]where two millionaires try to compare who is richer without information leaking. Based on Yao’s research, a variant of the millionaire problem named the socialist millionaire problem[2,3]was proposed. On this condition,two millionaires wish to compare whether they are equally rich. However,Lo[4]pointed out that constructing an equality function with only two-party is not secure. Thus, a semi-honest third party(TP)should exist to complete the task.

With the advancement of quantum mechanics,laws such as the Heisenberg uncertainty principle and the quantum no-cloning theorem were discovered. They endow quantum computing with absolute security. With this advantage,a huge number of quantum cryptography protocols have been proposed to solve cryptography challenges, embracing quantum secure direct communication (QSDC),[5–8]quantum secret sharing (QSS),[9–12]and quantum key distribution(QKD),[13–17]as well as quantum secure multiparty computation(QSMPC),[18–24]etc.

As one essential type of QSMPC,quantum private comparison (QPC) has gotten much attention. In QPC protocols,the purpose of participants is to determine whether the respective secrets are equal. According to the number of participants, the types of QPC protocols can be divided into twoparty and multi-party. The two-party QPC protocols are taken for example. The inputs are their secretsxandy. The output isx=yorx/=y. Yang and Wen[18]proposed the first QPC protocol with a dishonest TP.Two parties compare their secrets based on decoy photons and EPR pairs, and the oneway hash function ensures the security of the protocol. Before long,Chenet al.[19]introduced a more efficient QPC protocol based on triplet entangled states and single-particle measurement. Then, Tsenget al.[20]proposed a QPC protocol with EPR pairs, facilitating implementation and improving qubit efficiency to 50%. After that, Jiaet al.[21]suggested another QPC protocol based onχ-type genuine four-particle entangled states, whose efficiency is equal to 100%. In 2014, Chenet al.[22]proposed a protocol using a class of maximally entangled states as the information carriers. The implementation of this protocol can rely on a variety of particles, so it has more freedom in selecting quantum states than all prior protocols. To further improve efficiency,Xuet al.[25]proposed a QPC protocol based on four-particle GHZ states. Three secret bits can be compared at one time, which reduces the rounds of the protocol. In addition, some participants without quantum capabilities were considered by Chouet al.[26]in their QPC protocol firstly. Such protocols are called semi-quantum private comparison(SQPC)protocols. They are closer to reality because some participants may not be able to afford quantum equipment. Recently, Zhouet al.[27]and Wanget al.[28]proposed SQPC protocols withd-dimensional Bell states and GHZ states, respectively, improving efficiency and ensuring security.

After analyzing existing QPC protocols, we observe the extensive utilization of entangled states. However, some unfavorable conditions,such as the difficulty in preparing entangled states[29]and the security vulnerabilities,[30]limit the application of entangled states. Thus,protocols based on single photons have received widespread attention.[31–34]As a significant method to ensure the correctness and security of singlephoton based protocols, rotational encryption is introduced in various types of quantum protocols, such as quantum key exchange,[35]quantum designated verifier signature,[36]quantum image encryption,[37]etc.Additionally,rotational encryption can be applied to design QPC protocols[38,39]because the mapping of rotational encryption is homomorphic.

In this paper,we propose an efficient QPC protocol with polarized single photons, which is efficient and easy to realize. In our protocol, two players encrypt their secret integers with rotational encryption and single photons, and then they can privately compare their secrets with a semi-honest TP,who may misbehave alone but cannot conspire with other players.[40–43]The TP should initialize a quantum sequence at the beginning of the protocol and decrypt it at the end of the protocol. Two players’ core operation is encoding the secret into the quantum sequence.

In comparison to existing QPC protocols, our protocol provides the following advantages. First, without pre-shared keys,the qubit efficiency of our protocol is 100%on account of the application of the circular transmission mode.[44,45]In this mode, the photons will be transmitted along the circular path TP-player1-player2-TP. Second, our protocol has simple technical requirements. The complex technology,such as entangled states, joint measurement, and entanglement swapping,are replaced by single photons,single-particle measurement,and unitary operation. As a consequence,the efficiency of our protocol achieves the theoretical maximum, and our protocol is easy to realize.

The rest of this paper is organized as follows. In Section 2, the encryption and decryption method with the rotational encryption is elaborated as a core. In Section 3, we propose a new QPC protocol.In Section 4,the correctness,security,and efficiency are analyzed. In Section 5,we compare our protocol with others and discuss its extended application.In Section 6,we summarize the characteristics of the protocol.

2. The encryption and decryption method of the protocol

The encryption and decryption method with the rotational encryption is the core of our protocol. The classical binary data“0” can be encoded to the horizontally polarized photon|0〉, and the classical binary data “1” can be encoded to the vertically polarized photon|1〉.

The rotational encryption operator,drawing support from Jones matrix,[46]can be expressed in the following form:

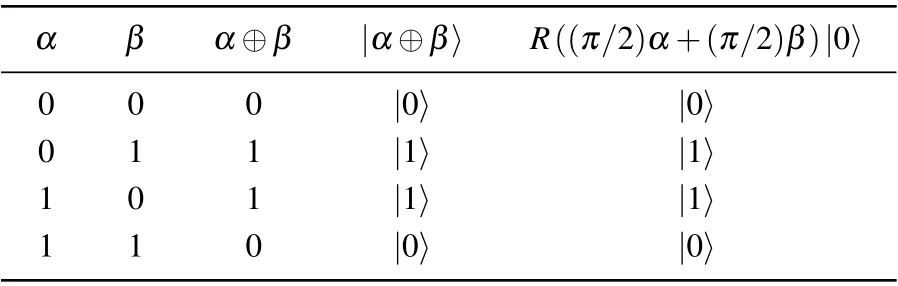
Table 1. The relationship among α, β, α ⊕β, |α ⊕β〉, andR((π/2)α+(π/2)β)|0〉.

From Table 1, we can discover that|α ⊕β〉andR((π/2)α+(π/2)β)|0〉are always equal. Thus,

The Lemma 2 follows.

It means thatR(θ)|α ⊕β〉can be expressed as the formE(π/2)α+(π/2)β[R(θ)|0〉],i.e.,we can realize the bitwise XOR operation with the rotational encryption.

3. The two-party quantum private comparison protocol

There are two distrustful players, Alice and Bob, who want to compare whether their secrets are equal with the aid of a semi-honest TP named Charlie.

Step 4 Alice generates her secret keyKA={kA,i:0≤kA,i ＜2π,i=n-1,...,1,0}randomly. Then she getsSAby handlingSinitwith her binary stringNA,n-1...NA,1NA,0and the keyKA. The process can be written in the following form:

Step 7 Alice and Bob announce their keysKAandKB,and then Charlie logs them.

Step 8 Charlie decryptsSBwith his private keyKCand the published keysKA,KB. He computesSCadhering to the following rule:

4. Analysis

In this section, we shall demonstrate the correctness and security of our proposed protocol.

4.1. Correctness

In this subsection,we give a general proof of the correctness of the protocol. In our analysis, decoy photons are ignored since they are only applied to detect eavesdroppers.

For any|φC,i〉inSC, we can rewrite it into the following form according to the operation rules of Alice, Bob, and Charlie:

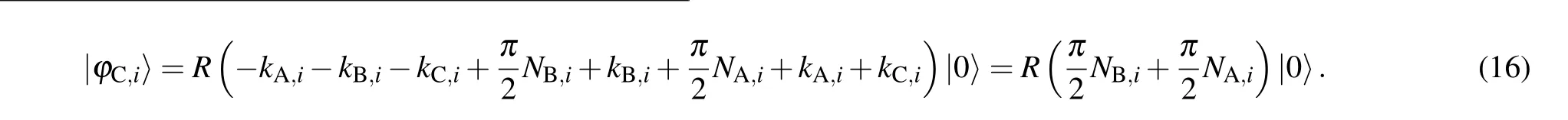
Then we can infer that|φC,i〉=|NA,i ⊕NB,i〉in the light of Lemma 2.

For simplicity, the stringNA,n-1⊕NB,n-1,...,NA,1⊕NB,1,NA,0⊕NB,0will be recorded inNA⊕NB. Obviously,NC=NA⊕NBholds based on Eq. (14). For this reason, an all-zeroNCrepresents thatNA=NB, and other cases signify thatNA/=NB. Thus,TP can determine the comparison result by figuring the stringNC.

4.2. Security analysis

We analyze the security of our proposed protocol. Firstly,we prove that our protocol can resist outside attacks.Secondly,we show that inside attacks are ineffective to our protocol.

4.2.1. Outside attack

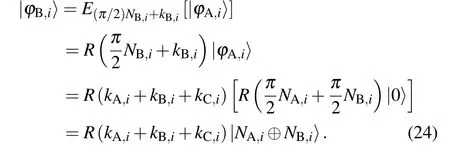
Unlike the security ensured by decoy photons in outside attacks, the inside security depends on the safety of the rotational encryption method,which is explained as follows.

We can infer that an attacker cannot identify the correct key for only an intercepted photon because when the photon is measured, it collapses to|0〉or|1〉, and the rotation angle is lost. Additionally, the measurement result cannot be guaranteed to be completely true once the attacker chooses a key unequal to the correct key. For example,the attacker choosesγ/=θto decryptR(θ)|0〉. The result isR(θ-γ)|0〉= cos(θ-γ)|0〉+sin(θ-γ)|1〉. Thus, the probabilitypthat the attacker gets the correct result|0〉by measuringR(θ-γ)|0〉with Z-basis is cos2(θ-γ). Sinceγandθare unequal,pcannot reach 100%,which means that a wrong key cannot decrypt the completely correct result.

Hence, we can analyze the inside attacks by judging whether participants can obtain a quantum sequence and the corresponding key simultaneously.Based on this idea,we will analyze the following four cases one by one: Alice wants to getNB, Bob wants to getNA, and Charlie wants to getNAorNB.

Case 1 Alice wants to getNB

NBonly exists inSB. However,the key(kA,i+kB,i+kC,i)to decryptSBis unavailable for Alice sincekC,iis only held by Charlie and never published during the whole period.

Another way for Alice to stealNBis to pass a fakeSAto Bob,such as a sequence filled by|0〉. While Bob sendsSBto Charlie, Alice intercepts it and passes another fake sequence to Charlie. If Bob announces his secret key, Alice can obtainSBandKBat the same time, soNBwill be leaked to Alice.However, this way is ineffective in our protocol. Once Alice interceptsSB,her eavesdropping behavior must be detected in the eavesdropping check before Bob publishes his secret key.Then the protocol will be rebooted with three refreshed keys so Alice can never have Bob’s available key.

In summary,Alice cannot obtainNB.

Case 2 Bob wants to getNA

CalculatingNAfromSAorSBare equivalent to Bob because it is Bob who encryptsSAtoSB. The former is taken for example. Bob cannot stealkC,ito decrypt the sequenceSAfor the same reason as Alice.

Similar to the above,Bob can replaceSinitwith a fake sequence filled by|0〉in Step 2. After Alice adds her secret to the fake sequence, Bob interceptsSAand then gives Charlie another random fake sequence. He may calculateNAafter the announcement of Alice’s key since the state of each photon inSAis in this form:|φA,i〉=E(π/2)NA,i+kA,i[|0〉]=R(kA,i)|NA,i〉.Nevertheless,the attack from Bob in this way is failed either.His eavesdropping will come to light after the check between Charlie and Alice.

To sum up,Bob cannot gainNA.

Case 3 Charlie wants to getNA

Once Charlie intercepts the sequenceSA, his eavesdropping will be identified. Then Alice will execute this protocol again with a refreshed key. Without the new key,Charlie cannot determineNAeven if he interceptsSA.As for the sequenceSB,Charlie can computeNA⊕NBfrom it legally,butNAandNBare invisible to him.

So,Charlie will fail to decryptSAorSBto stealNA.

Case 4 Charlie wants to getNB

As already stated,NBhas never been transmitted separately when the protocol is executed normally. It only coexists withNAinSBand never be divulged unlessNAis known.However,NAis unavailable for Charlie from the analysis in Case 3.

In another way, Charlie can replaceSAwith a fake sequence filled by|0〉. Then he may calculateNBfromSBafterKBis published by Bob. Nevertheless, this behavior can also be discovered due to the check between Alice and Bob.

Therefore,NBwill not be disclosed to Charlie.

According to the above study,this protocol can withstand outside and inside attacks without revealing the players’ private integers.

4.3. Efficiency analysis

The definition of qubit efficiencyη=ηc/ηtis given in Refs.[20,40]. In the above equation,ηcrepresents the number of the compared classical bits andηtrepresents the total number of particles in the comparison protocol except for decoy particles used in the eavesdropping check.[20,40]Particularly,ηt=ηk+ηs. Here,ηkrefers to the number of quantum particles applied to pre-shared keys,such as in QKD protocols,andηsrefers to the number of qubits carrying information in the sequence.

For our protocol,pre-shared keys do not exist,i.e.,ηk=0.Moreover, the comparison of each classical bit in this protocol needs to be completed by one quantum bit,i.e.,ηs=ηc.Therefore,the efficiency of our protocol is 100%.

5. Discussion

In this section, we will compare our protocol with other similar protocols,and then discuss the extra application of our protocol.

In Table 2, we compare protocols in Refs. [21,32,49,50]with our protocol. Our protocol has the following characteristics: First,it is unnecessary to utilize extra particles during the key distribution process. Thus, our protocol has no quantum resources consumption of key distribution compared to a series of QKD-based QPC protocols.[32,49,50]Second, the quantum resources in our protocol are multiplexed. It means that the same quantum sequence carries two players’ secret integers.However,in some protocols[49,50]without this feature,players have to prepare more particles to execute the protocols,which increases the consumption of quantum resources. Third, our protocol not only achieves the maximum theoretical efficiency as Jiaet al.’s protocol,[21]but can be realized more easily.Jiaet al.’s protocol[21]has more technical constraints, such as preparing four-particleχ-type states, entanglement swapping,and joint measurement.[44]On the contrary,our protocol is realized with single photons,unitary operation,and singleparticle measurement.

Table 2.Comparison among our protocol and some existing QPC protocols.

Furthermore,our proposed protocol can also be extended to perform additional tasks. For example,the protocol can accomplish a comparison of two sets. Every player arranges the set elements from small to large, and then concatenates the binary values. Another example is quantum secret sharing.Assume that the boss split a secret integerNCinto a randomNAandNB=NA⊕NC, and then sentNAto Alice andNBto Bob. Alice and Bob can execute our protocol to calculate the secretNC.

6. Conclusion

We propose an efficient QPC protocol with single photons and rotational encryption. With the help of a TP, the players can safely determine the size relations for two private integersNAandNB. For efficiency, the secret keys in our protocol are distributed through classic channels instead of QKD protocols, so extra particles are not consumed for sharing keys.Additionally,the circular transmission mode allows players to implement the multiplexing of quantum resources, reducing the number of photons utilized in our protocol. According to these two characteristics, the qubit efficiency of our protocol reaches 100%, the theoretical maximum. For technical constraints, the utilization of single photons, unitary operation,and single-particle measurement allows our protocol to be realized under current technical conditions.

Acknowledgments

Project supported by the National Key Research and Development Program of China(Grant No.2020YFB1805405),the 111 Project (Grant No. B21049), the Foundation of Guizhou Provincial Key Laboratory of Public Big Data(Grant No.2019BDKFJJ014), and the Fundamental Research Funds for the Central Universities(Grant No.2020RC38).