Tunable spectral shift of high-order harmonic generation in atoms using a sinusoidally phase-modulated pulse

Yue Qiao(喬月) Jun Wang(王俊) Yan Yan(閆妍) Simeng Song(宋思蒙) Zhou Chen(陳洲)Aihua Liu(劉愛華) Jigen Chen(陳基根) Fuming Guo(郭福明) and Yujun Yang(楊玉軍)

1Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

2Department of Physics and Materials Engineering,Taizhou University,Taizhou 318000,China

Keywords: high-order harmonic generation,spectra shift

1. Introduction

When atoms and molecules are illuminated by an intense femtosecond laser pulse, electron motion can be modulated periodically and a series of novel physical phenomena arise.[1–6]The rescattering model (collision of the ionized electron with its parent ion in the laser electric field)[7,8]can be used to understand these nonlinear and nonperturbative phenomena of above-threshold ionization as well as highorder harmonic generation (HHG).[9–13]Within low beam divergence[18]and good coherence properties[19]inherited from the driving laser, HHG is the most reliable pathway for producing a coherent light source with spectra from extreme ultraviolet(XUV)to soft x-ray.[20–22]Owing to its wide spectrum,HHG is an important way to produce optical pulses with an attosecond duration.[14–17]HHG can occur in every half cycle of the laser field. According to semiclassical model,[7]high-order harmonic emission occurs through the following three steps: the electron first tunnels through the effective potential barrier formed by the laser field and the atom,then the ionized electron accelerates along the laser electric field, and finally, the electron returns to the parent ion and recombines with the ground state.

As the response of electrons can be affected by the laser field, the process of HHG can be directly initiated using the temporal structure of the laser pulse. In particular, control of the spectral phase of the pulse, and thus its temporal profile, has been demonstrated effectively to give control over numerous physical systems and processes.[23–26]Many theoretical and experimental studies have been carried out to control HHG by modulating the driving laser pulse. For instance, negative frequency chirp atomic HHG is produced by rapidly varying the intensity of ultrashort laser pulses.[27]Several works have focused on the effect of the laser chirp condition on the spectral structure of high-order harmonics emitted from atoms.[27–29]The influence of the carrier envelope phase on a laser-driven dynamic process has been precisely investigated.[30–32]Strobe gating schemes are usually proposed and employed for extending the plateau structure of HHG,such as the polarization gating,[33]amplitude gating,[34]polychromatic laser field[35]and the more complicated double optical gating[36]approaches. Also,the spatial characteristics of inhomogeneous fields and confinement of electron movement play an important role in the HHG process[37–39]and lead to the generation of even harmonics.[39,40]

Given that coherent XUV and x-ray sources are important tools for atomic spectroscopy,characteristics of HHG can be beneficial for applications that require a spectrally tuned single harmonic. Photon energy-tunable XUV radiation is very important in many fields such as spectroscopy,[41]XUV holography[42]and nanolithography.[43]Shaping or tuning the generated harmonics can be achieved by the use of special pulse shapes(e.g., trapezoidal and sine-square like). Oldalet al. proposed employing double pulses to generate high-order harmonics with tunable photon energy and spectral width.[44]In other words, the root of spectrally tuned single harmonics is the frequency shift of HHG spectra. Frequency modulation in HHG results from two points: a rapid change envelope effect for ultrashort laser pulses and the propagation effect. The propagation effect is negligible if the intensity of the laser pulses and the density of atoms are low. For an instance,Gaussian pulses include a rising and a falling part. In the rising part,compared with the previous cycle,free electrons obtain more kinetic energy from the laser electric field due to the stronger driving force, thus a frequency blueshift appears in the HHG spectra. In the same way,a redshift occurs on the falling part.This frequency chirp has a similar effect to an amplitude chirp.[27]A blueshift in HHG can be achieved easily by using an intense long laser pulse that interacts with atoms and has been extensively studied theoretically.[45–47]A redshift in molecular HHG was studied to probe nuclear motion.[48,49]However,to our knowledge,redshifting in atomic HHG without consideration of the propagation effect has not been reported.

In this paper, we investigate atomic harmonic spectra in the interaction between helium atoms and a sinusoidally phase-modulated laser pulse. Wollenhauptet al. investigated the physical mechanism of strong-field quantum control by shaped femtosecond light fields.[50]We noticed that the frequency domain modulation character of the electric field not only plays an important role leading to a shift in the atomic harmonic spectra but is also a new route for tuning the harmonic central frequency. By simply adjusting the phase parameters in the frequency domain of the incident laser pulses,one can acquire wavelength tuning of the high-order harmonic.This manuscript is organized as follows. Section 2 describes our theoretical model and the numerical method used in this work. In Section 3 the impact of the modulated electric field of laser pulses on spectral modulation in atomic HHG is discussed. Section 4 presents a short summary.

2. Theory

We investigated the influence of the total electric field on the HHG process. For a pulse in the linear transform limit, the temporal electric field is expressed asE(t) =(1/2)E0f(t)eiω0t+c.c., whereE0is the peak amplitude of the electric field,f(t) is the envelope of the pulse (assumed to be of Gaussian shape)andω0is the center frequency. Our laser pulse is realized by a simple and intuitive pulse shape parametrization, since the physical mechanism of quantum control using sinusoidal phase modulation in the frequency domain has also been discussed in the time domain,[50]and the properties of the modulated pulses are briefly summarized in the following. As shown in Fig.1(upper panel),we start with a transform limit laser pulseEin(t)=(1/2)E0f(t)eiω0t+c.c.The initial electric intensity, full width at half maximum(FWHM) and wavelength of the driving laser pulse areE0=0.16, 10 optical cycles and 800 nm, respectively. Through Fourier transformation,we can obtainEin(ω)in the frequency domain. We can modulate the electric field by adding a phase modulation parameter ～Eout(ω) = ～Ein(ω)eiφ(ω). In the frequency domain, the phase function isφ(ω) =Asin(ω-ωref)T+φ, whereAdescribes the amplitude of the phase modulation function,Tis the frequency of the sinusoidal oscillation andφis an absolute phase offset,ωref=0.057. Finally, we gain a new temporal envelope functionEout(t) by applying the inverse Fourier transform. The temporal profile of a shaped laser electric field is shown in Figs.1(a)and 1(b).Figure 1(a) shows how the temporal evolution changes when the frequency of the sinusoidal oscillationT=1400(solid red line) andT=2000 (solid blue line) andA=0.5 andφ=πare adopted: the symmetry of the pulse shape of laser is broken, especially in green zone, and the pulse in rising part is not equal to that in the falling part. In Fig. 1(b), we fixedA=0.5 andT=1400: whenφ=0(solid red line)andφ=π(solid blue line),in the time domain,inversion symmetry can be found between them.

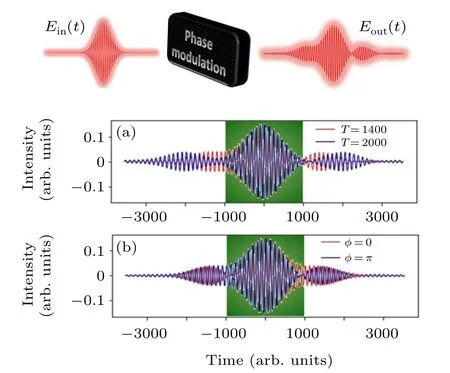
Fig. 1. Temporal evolution of a sinusoidally phase-modulated laser electric field for different frequency phase parameters. All panels are for an intensity of 0.16 and central wavelength of 800 nm. (a) For fixed φ =π, the corresponding new envelope for different T [T =1400 (solid red line) and T =2000(solid blue line)].(b)The corresponding temporal amplitude of the new envelope at a fixed T =1400 for different absolute phase offsets φ.

3. Results and discussion

We present the harmonic spectra of He atoms irradiated by a sinusoidally phase-modulated pulse with different oscillation frequenciesT(Fig. 2). The parameters selected in the calculation areA=0.5,φ=πandE0=0.16,withTchanging from 1400 to 2000. The harmonic range given in Fig. 2 represents lower-order harmonics (31–35 orders). It can be seen from Fig.2 that under the driving of a sinusoidally phasemodulated pulse, the harmonic intensities of He atoms under different parametersTare significantly different. The photon energy of the generated harmonics is modulated within the range of 1 eV–a bandwidth comparable to the photon energy of the fundamental field. When theTis small,an obvious redshift from harmonics can be observed. With increase inT,the harmonic peak position gradually moves to the high-energy region and the redshift of the harmonics becomes smaller. However, whenTis greater than 1700, the peak position of the harmonics is almost unchanged and the phenomenon of harmonic redshift disappears.

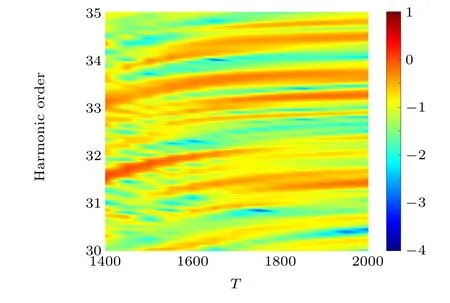
Fig. 2. Variations of the harmonic intensity with different values of the parameter T.

In general,the rising part of the laser field leads to a positive chirp in HHG,where dI(t)/dt ＞0,leading to a blueshift.On the contrary, the falling part of the laser field leads to a negative chirp in HHG,where dI(t)/dt ＜0,leading to a redshift. When the rising and falling parts of the laser are symmetrical, the blueshift and redshift can cancel each other out,and the spectral shift from harmonics cannot be observed. In order to study the phenomenon of harmonic spectral shift for differentTvalues, we present the envelope intensity of the shaped laser electric field whenT=1400(solid red line)andT=2000 (solid blue line) in Fig. 3. The other field parameters are consistent with Fig. 2. As can be seen from Fig. 3,there is a main pulse and two sub-pulses at differentT. WhenT=1400, the distance between the sub-pulses and the main pulse is small, and the first incident sub-pulse will interfere constructively with the main pulse. The overall pulse presents an asymmetrical distribution relative to the intermediate moment. The rising part of the pulse will have a higher intensity than the falling part, resulting in a large change in the harmonic frequency. WhenT=2000, the sub-pulse gradually moves away from the main pulse, and the overall pulse tends to have a symmetrical structure, so the harmonic peak position hardly changes. Through the above analysis, we know that the parameterTcan change the time delay between the main pulse and the sub-pulses of the laser electric field after shaping, thereby changing the overlap of different sub-pulses of the laser electric field and finally giving the laser field an asymmetric structure and shifting the harmonic spectrum. The ionization probability of the shaped pulses with oscillation frequencyT=1400 andT=2000 interacting with He atoms is shown in the inset of Fig.3.By comparing the ionization probability,we find that ionization mainly occurs at the time when the main pulse takes effect; we therefore mainly focus on the effect from the main pulse.

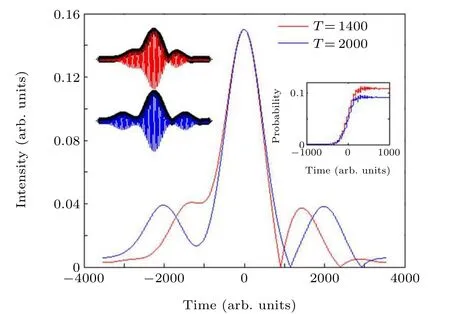
Fig. 3. The envelope intensity of the sinusoidally phase-modulated pulse when T =1400 (solid red line) and T =2000 (solid blue line). The inset shows the ionization probability of an He atom.

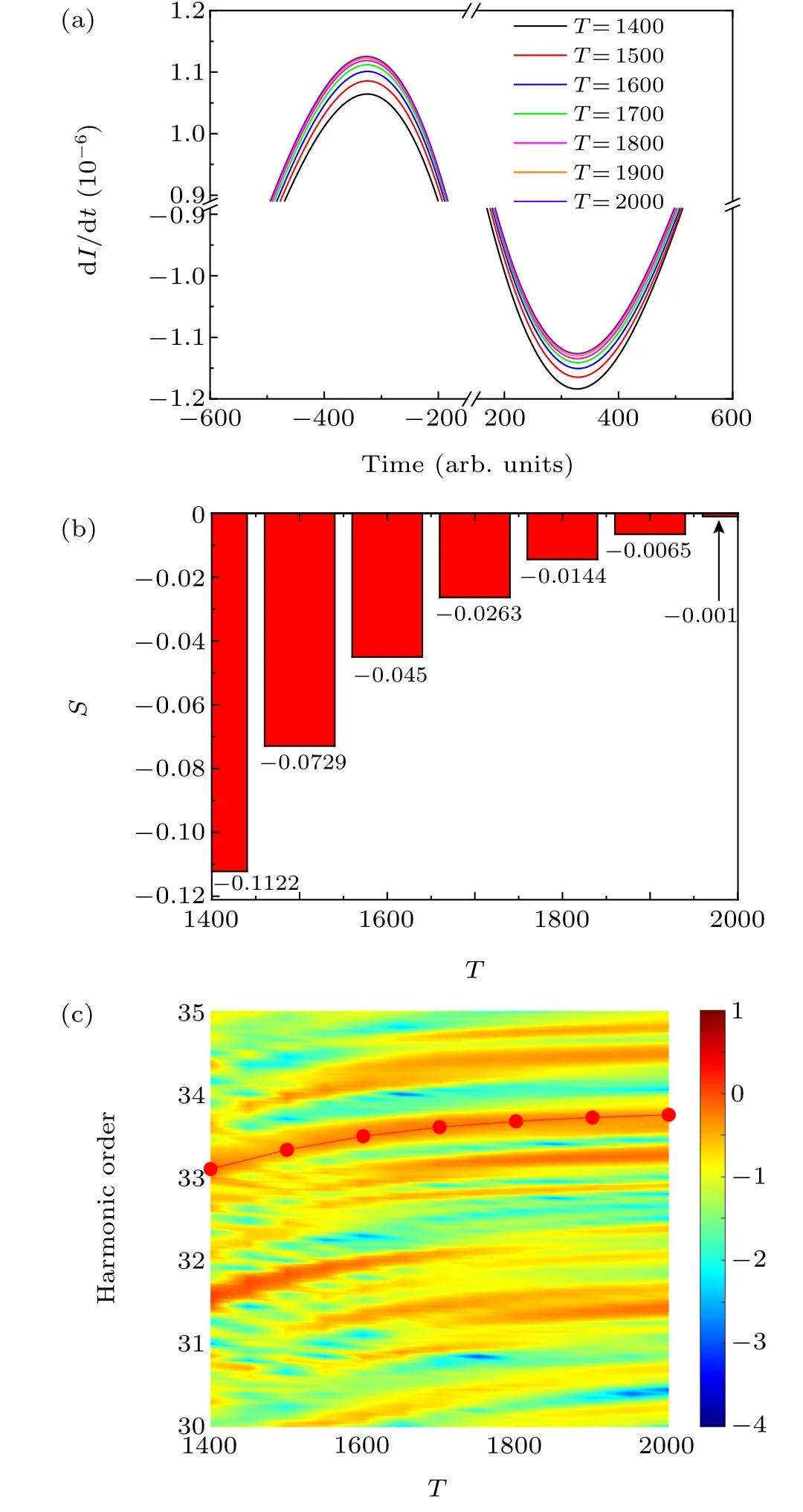
Fig. 4. (a) The derivative of intensity versus time and (b) the asymmetric coefficient as a function of the oscillation frequency T. (c) Comparison of the harmonic spectrum and the asymmetry coefficient.

The harmonic intensity is affected not only by the oscillation frequencyTbut also by the absolute phase offsetφ.Figure 5(a)shows the harmonic spectra of He atoms as a function ofφ. The parameters selected in Fig. 5(a) areA=0.5,T=1400,andE0=0.16,whileφchanges from 0 to 2π. We can see from Fig. 5(a) that the emission intensity of the 40–45th order harmonics has an oscillating structure with change ofφ. Under the modulation ofφ, the peak of the harmonic spectrum moves significantly. In the process of changing from 0 toπ, the peak of the harmonic moves to a low-energy region, and in the process of changing fromπto 2π, the peak of the harmonic moves to a high-energy region. This is because the phase offset can be changed byφ, and the phase difference between the sub-pulse and the main pulse can be changed without changing the amplitude of the main pulse and the sub-pulse, as shown in Fig. 5(b). Whenφ=0, the rising part changes faster than the falling part, where dI(t)/dt ＞0,leading to a blueshift. On the country,the falling part changes faster than the rising part whenφ=π, where dI(t)/dt ＜0,leading to a redshift. In this way,the asymmetry of the rising and falling parts of the laser pulse is adjusted, and the frequency peak position of the harmonic emission is adjusted.The asymmetric coefficient as a function of the absolute phase offsetφis shown in Fig.5(c). We can see that the asymmetry coefficient shows a symmetrical structure relative toφ=π.During the change from 0 toπ, the asymmetry coefficient changes from positive to negative and harmonics change from blueshift to redshift, so the peak of the harmonic moves to a low-energy region. During the change from 0 to 2π,the asymmetry coefficient changes from negative to positive and harmonics change from redshift to blueshift, so the peak of the harmonic moves to a high-energy region.

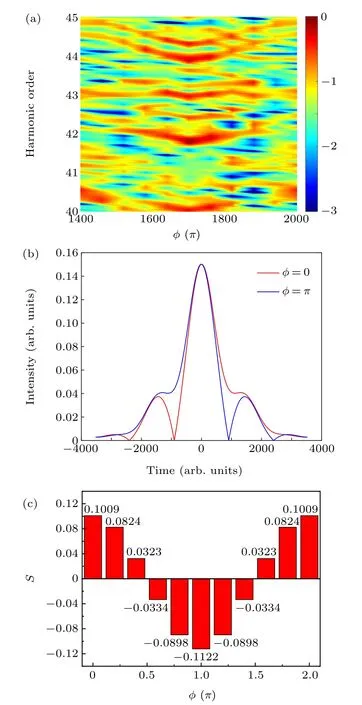
Fig.5.(a)Harmonic intensity as a function of the parameter φ. (b)The envelope intensity of the sinusoidally phase-modulated pulse when φ =0 (solid red line) and φ =π (solid blue line). (c) The asymmetry coefficient as a function of the absolute phase offset φ.

4. Conclusions and final remarks

The frequency modulation of atomic high-order harmonics by a sinusoidally phase-modulated pulse is investigated theoretically. We have numerically solved the onedimensional TDSE based on a single active-electron model.It is found that the spectral shift of a high-order harmonic can be observed when the symmetry of the pulse shape of the laser is broken. The shape of our pulse in the rising part is not equal to that in the falling part. The rising part of the laser field leads to a positive chirp in HHG,where dI(t)/dt ＞0,leading to a blueshift. On the country,the falling part of the laser field leads to a negative chirp in HHG,where dI(t)/dt ＜0,leading to a redshift. The asymmetry coefficientSbetween the rising and falling parts is shown: asTincreases,Sbecomes smaller.The shift in the frequency peak position decreases gradually.Our procedure gives the possibility of tuning the central wavelength of the driving source itself. Spectral shifting of highorder harmonics is observed due to the failure to balance between the blueshift and the redshift. This shift in atomic harmonic spectra can be controlled by changing the phase parameters in the frequency domain. Tunable high-order harmonics should also prove useful as a seeding pulse for x-ray lasers.We predict that in the near future a spectral shift can be observed by means of this scheme using propagation effects.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.11604119,11627807,11774129,11774131, 11904120, 11975012, and 91850114) and the Outstanding Youth Project of Taizhou University (Grant No.2019JQ002).