Influences of Marangoni convection and variable magnetic field on hybrid nanofluid thin-film flow past a stretching surface
Noor Wali Khan Arshad Khan Muhammad Usman Taza Gul Abir Mouldi and Ameni Brahmia
1Department of Mathematics,City University of Science and IT,Peshawar 25000,Pakistan
2College of Aeronautical Engineering,National University of Sciences and Technology(NUST),Sector H-12,Islamabad 44000,Pakistan
3Higher Education Archives and Libraries Department KP,Govt. Superior Science College,Peshawar,Pakistan
4Department of Industrial Engineering,College of Engineering,King Khalid University,Abha 61421,KSA
5Chemistry Department,College of Science,King Khalid University,Abha 61413,Saudi Arabia
Keywords: thin-film flow,hybrid nanofluid,viscous dissipation,stretching surface,homotopy analysis method
1. Introductio n
Recently thin-film flow has obtained considerable significance due to its important applications at the industrial level such as coating of fibers and cables,cooling of metallic plates,processing of foodstuffs,extrusion of plastic surface thinning and annealing of copper wires.[1]Researchers have been inspired by the pioneering work of Wang,[2]who investigated the time-dependent flow of a thin film over a stretchable surface. Wang’s[2]ideas were further extended by Anderssonet al.[3]to improve heat transmission characteristics.Afterwards,Liu and Andersson[4]presented the idea of thin-film flow in a more generalized form.Wang[5]performed an analytical solution using the homotopy analysis method(HAM)for thin-film flow upon a time-dependent stretched sheet. Wang compared the results of HAM with the numerical solution and found a good agreement between the results. Iqbalet al.[6]analyzed thin-film flow upon an unsteady surface using thermophoresis effects and Brownian motion. They observed that the thermal profiles were augmented by a corresponding increase in Brownian and thermophoresis parameters. Sadiq[7]analyzed the thermal characteristics for thin-film nanoparticles upon a stretched surface by using the temperature of the surface and an internal heat generation source. Sadiq used water as the base fluid with copper, titanium and alumina nanoparticles,and proved that augmentation of the volumetric fraction of solid nanoparticles reduced the flow and enhanced the thermal characteristics.
The suspension of small-sized particles (of a size<100 nm, i.e., nanoparticles) in a base fluid results in a nanofluid.[8,9]It has been proved experimentally[8]that nanofluids has higher thermal flow characteristics than traditional fluids.Additionally,hybrid nanofluids have attracted the attention of researchers due to their wide range of applications in the fields of medicine,nanotechnology and the phenomenon of thermal transmission. Khanet al.[10–12]published an excellent analysis of heat transmission by hybrid nanofluids using various flow conditions and different graphical views. They proved that the rate of thermal flow is much better for hybrid nanofluids compared with traditional fluids. Due to the use of hybrid nanofluids, as investigated by Hayatet al.,[13]applications in many fields such as biomedicines, conservation of energy,ceramics,optics and nanotechnology have been updated. Khanet al.[14]researched the thermal flow of a carbon nanotube nanofluid between two rotating plates. The authors of this investigation used various flow conditions and highlighted that thermal diffusivity of the fluid was augmented with enhancement in thermal radiation and Brownian motion.Pal and Mandal[15]discussed the flow of a hybrid nanofluid past a stretched surface with impact of a magnetic field. Xuet al.[16–19]carried out some impressive work to improve the flow and heat transfer of a nanofluid by using various flow conditions with different geometrical views. In these investigations the authors made an attempt to fill the gaps in the existing literature.
Viscous dissipation is caused by devastation of a fluctuating velocity gradient due to viscous stresses. This irreparable procedure normally leads to the conversion of kinetic energy to internal energy of the fluid and causes heating of the flow system. Pop[20]analyzed the idea of energy dissipation and transportation at the nanoscale and also highlighted that this concept is of great importance in designing energy conservation systems and energy-efficient circuits. Aliet al.[21]examined the impact of viscous dissipation upon thermal flow for hybrid nanoparticles in a porous channel. It was noticed in that study that the thermal profiles were augmented with the enhancement of energy dissipation. Sharmaet al.[22]inspected the effects of forced convection heat transmission on time-dependent fluid flow between rotary discs. In that work the authors used the basic concept of the Neuringer–Rosensweig model for flow equations. They noted that the dissipation parameter caused an augmentation in thermal flow.Augustoet al.[23]employed the concept of thermal flow and viscous dissipation for the reduction of friction inside a greasefilled labyrinth seal. They used an Arrhenius-type equation in their mathematical modeling. Khanet al.[24–26]analyzed the augmentation of heat transfer and thermal flow by a thin moving needle surrounded by a moving fluid. In these investigations, the authors used the impact of viscous dissipation along with other flow conditions and established that thermal flow and heat transmission were augmented by enhancing the values of the viscous parameter.
The inspection of viscous fluid flow upon a stretching surface is of significant importance due to practical applications in numerous manufacturing procedures such as copper wire drawing,fabrication of glass,stretching of artificial fibers and plastic films,and polymer extrusions,etc. The performance of the final product depends upon the rate of mass and thermal flow over the stretching surface, as examined by Karwe and Jaluria.[27]Lundet al.[28]analyzed the Tiwari and Das model using the thermophoresis characteristics of nanoparticle fluid flow upon a porous stretching surface. In that study, the authors used copper and alumina nanoparticles in water as the base fluid. Abbaset al.[29]investigated the inclined stretching surface of the flow of a hybrid nanofluid using the Xue and Yamada–Ota models. Zainalet al.[30]highlighted the stability concept of a magnetohydrodynamic nanoparticle flow upon a stretching sheet with the squared velocity term. Anuaret al.[31]explored the effects of buoyancy on hybrid nanofluid flow over a stretching plate using silver and magnesium oxide nanoparticles. They noted that velocity declined while thermal flow was enhanced with increased volumetric fraction of nanoparticles. Readers can find more information about the related work in Refs.[32–41].
Several investigations have been conducted into thin-film flow over a stretching sheet by employing different flow conditions,but no work has yet been carried out on thin-film flow of a hybrid nanofluid with variable viscosity influenced by Marangoni convection, which is the main motivation for this work. In the current work,a stretchable surface is considered upon which flow of a hybrid nanofluid thin film is taken into account. The current work focuses on the idea of augmenting heat transmission by making use of a hybrid nanofluid. The equations that govern the flow problem will be converted to dimensionless form by employing a set of similar variables. The resultant set of equations will then be solved by using HAM.
2. Mathematical formulation
Consider an unsteady two-dimensional thin-film flow of a hybrid nanofluid upon a stretching surface affected by a magnetic field applied in the direction normal to the flow of fluid.The stretched velocity of the surface isUw=bx/1-at,wherebandγare fixed values. To augment the heat transfer characteristics of the fluid flow,titanium oxide and silver nanoparticles were incorporated into the base fluid. The flow is also influenced by variable viscosity and Marangoni convection. The fixed concentration and temperature of the hybrid nanofluid areC0andT0, respectively, whereas these respective quantities at the surface of the sheet areCw(x,t)=Cr(bx2/2ν)(1-at)-3/2andTw(x,t) =T0-Tr(bx2/2ν)(1-at)-3/2withCrandTrbeing the reference values of the nanofluid, such that 0<Cr<C0and 0<Tr<T0.
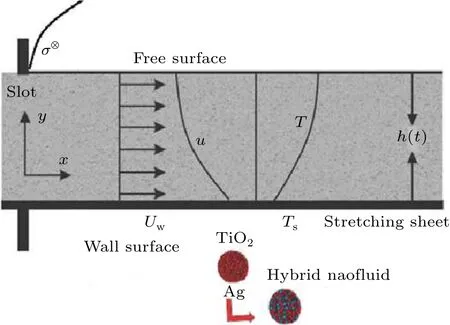
Fig.1. Graphical view of the flow problem.

2.1. The Reynolds model
In this model,


Some physical parameters are encountered while changing the governing system of equations to dimensionless form, which are defined mathematically as

The thermophoresis characteristics of traditional and hybrid nanofluids are shown in Table 1 while their numerical values are given in Table 2.

Table 1. Thermophysical characteristics of TiO2 and(TiO2+Ag/blood)nanofluid.[42]

Table 2. Numerical values of TiO2 and TiO2+Ag/blood nanofluid for thermophysical properties.
3. Solution method
It is a common observation that most physical phenomena when modeled mathematically give rise to a nonlinear equation. Sometimes,the resultant set of equations is highly nonlinear. To solve such models,researchers and mathematicians have designed certain tools and techniques. HAM[12,43,44]is one technique that is used to determine the semi-numerical solution to such problems. This method requires some starting values,which are defined below.
The operatorsπf,πΘ,andπΦin linear form are expressed as

4. Discussion of results
In the current work, a stretchable surface is considered upon which hybrid nanofluid thin-film flow is taken into account. In this work we consider the idea of augmentation of heat transmission by making use of a hybrid nanofluid. The flow is affected by variations in the viscous forces along with viscous dissipation effects and Marangoni convection.A timeconstrained magnetic field is applied in the direction normal to the flow system. During the conversion of the equations that govern the flow system into dimensionless form, some physical parameters have been encountered. The effects of these parameters upon flow profiles are now discussed in detail with the help of a graphical view,as given below.
4.1. Flow characteristics
The impact of variations in different emerging parameters upon flow profiles is depicted in Figs.2–5.
Figure 2 shows that change in the magnetic parameterMreduces the flow profiles. Physically this can be interpreted as follows: with increasing value ofMa Lorentz force is produced that acts in the opposite direction to the flow of fluid and causes resistance to the fluid’s motion. Due to these resistive effects the fluid flow declines.
Figure 3 shows that an increase in the value of the viscosity parameterΛresults in a reduction of the velocity profiles.Actually,with an increase in the value ofΛthe viscous forces increase,and as a result more resistance is experienced by the nanoparticles during motion.In this physical phenomenon,the thickness of the momentum boundary layer is reduced, causing the velocity profiles to decline.
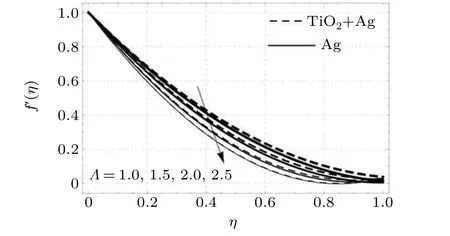
Fig.3. Flow profiles versus viscosity parameter.
From Fig. 4 we can see that velocity is reduced in response to an increase in the unsteadiness parameterS. Physically this can be interpreted as follows: an increase in the value ofScauses more resistive force to the fluid motion and increases the skin friction. In this whole process,the strength of the momentum layer is reduced, ultimately decreasing the velocity of the nanoparticles.
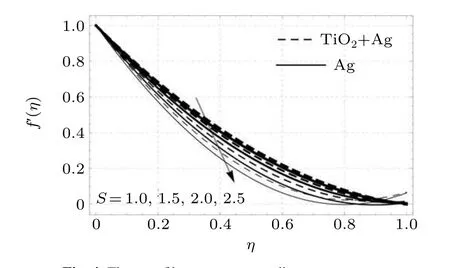
Fig.4. Flow profiles versus unsteadiness parameter.
Figure 5 shows the impact of the thin-film parameterβupon the flow of fluid. An increase in the value ofβleads to strengthening of the thickness of the momentum boundary layer,as a result of which the flow characteristics of the fluid increase.
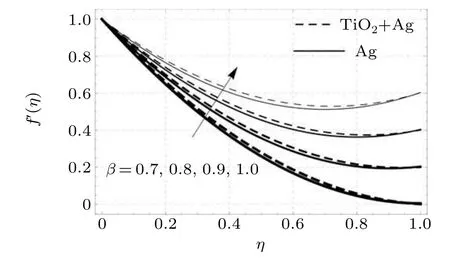
Fig.5. Flow profiles versus thin film parameter.
4.2. Thermal characteristics
The impact upon flow profiles in response to variations in different emerging parameters has depicted in Figs.6–9.
A change in thermal profiles in response to variations in the Eckert numberEcis presented in Fig.6.It can be observed that with a growth in the value ofEcthe transmission of energy increases from higher to lower regions. In this process kinetic energy changes to heat energy,leading to growth in the thermal profiles.

Fig.6. Thermal profiles versus Eckert number.
Figure 7 depicts that the thermal characteristics decline with augmentation in Prandtl numberPr. Actually, at lower values ofPrmore heat diffuses while at higher values ofPrless heat diffuses. Hence an increase in the value ofPrcauses a reduction in thermal diffusion,leading to a decline in thermal characteristics.
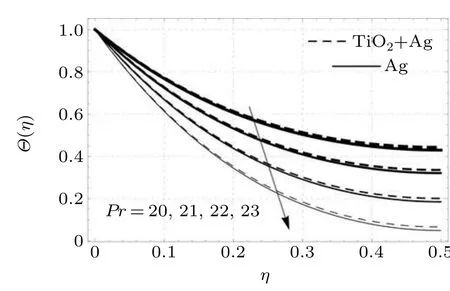
Fig.7. Thermal profiles versus Prandtl number.
Figure 8 depicts that for increasing values of the unsteadiness parameterSmore heat transfer occurs from regions of higher concentration to lower ones.This phenomenon strengthens the thickness of the thermal layer and causes an enhancement in the heat transfer.
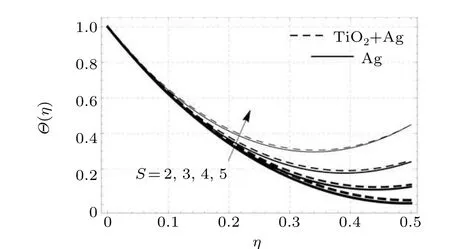
Fig.8. Thermal profiles versus unsteadiness parameter.
Figure 9 portrays the influence of variations in the viscosity parameterΛupon heat transmission.It can be noticed from this figure that for increasing values ofΛthe thickness of the thermal layer decreases,as a result of which there is less heat diffusion. In this physical process,heat transmission declines as depicted in Fig.9.
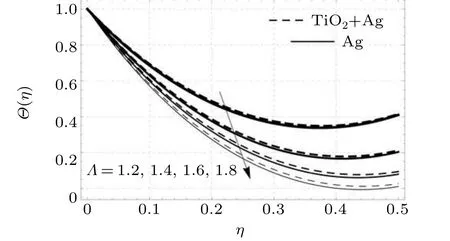
Fig.9. Thermal profiles versus viscosity parameter.
4.3. Discussion of the tables
The thermophysical properties of nanoparticles are presented in Table 1 while their numerical values are depicted in Table 2. The impact of various parameters on the thermal transfer rates for hybrid and traditional nanofluids is described numerically in Table 3. It can be seen that the Nusselt number increases with higher values ofEc, volumetric fraction of solid nanoparticles and the thin-film parameter while it declines with growth in the value of the viscosity parameter.The rate of heat transmission for hybrid nanoparticles has been noted to be much better than of a traditional nanofluid.A comparative analysis of current results and those published in the literature by Qasimet al.[45]was also carried out in the current investigation with regard to variations in common parameters.This comparison is presented in Table 4, where good agreement is noticed. In Fig.10 the percentage augmentation in the rate of thermal flow is presented with a comparison between TiO2nanoparticles and(TiO2+Ag)nanoparticles. From this chart, it is quite obvious that the rate of thermal flow varies from 3.77% to 9.02% when the values for TiO2nanoparticles range from 0.01 to 0.03 whereas for the same range for(TiO2+Ag) nanoparticles the thermal flow rate varies from 4.05% to 9.58%. This justifies that hybrid nanoparticles ensure a greater heat flow rate than traditional nanofluids.
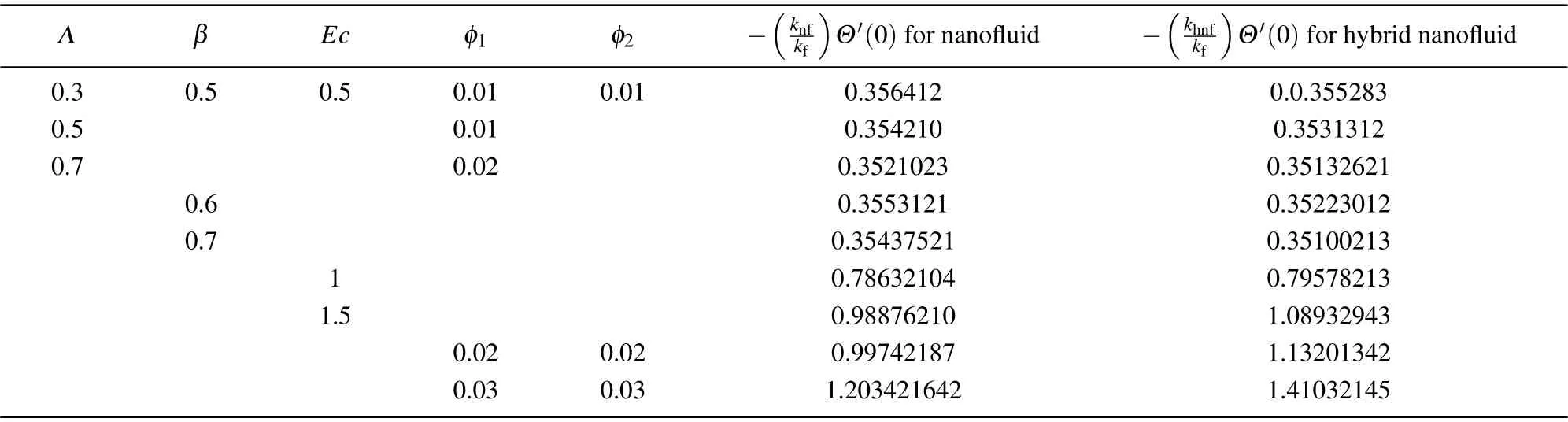
Table 3. Comparison of the heat transfer rate of nanofluids and hybrid nanofluids.

Table 4. Comparison of the values of the common parameters in the current work and the work of Qasim et al.[45]
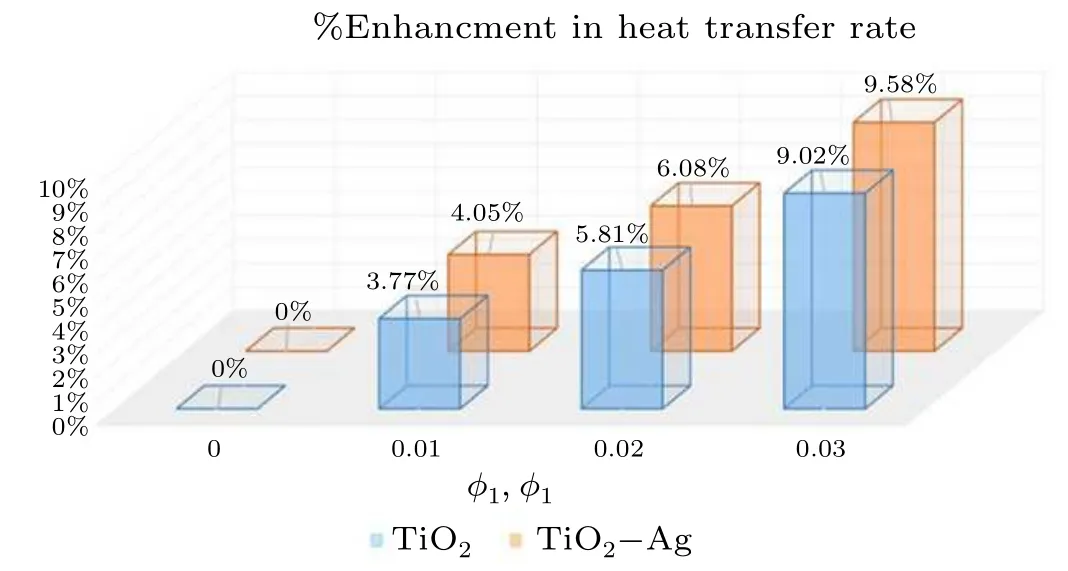
Chart. Percentage increase in heat transfer rate and comparison between nanofluids and hybrid nanofluids.
5. Conclusion
In this investigation, a stretchable surface is considered upon which a hybrid nanofluid thin-film flow is taken into account. In this work we focus on the idea of augmenting heat transmission by making use of a hybrid nanofluid. The flow is affected by variations in the viscous forces along with viscous dissipation effects and Marangoni convection. A timeconstrained magnetic field is applied in the direction normal to the flow system. During the conversion of the equations that govern the flow system into dimensionless form, some physical parameters are encountered. The effects of these parameters on the flow profiles have been discussed in detail with the help of graphs. After a detailed discussion of the work the following points can be noted:
· When increasing the values of the magnetic parameter a Lorentz force is produced that acts in the opposite direction to the fluid flow and causes resistance to fluid motion. Due to these resistive effects the fluid flow declines.
· As the values of the viscosity parameter increase the viscous forces increases, due to which more resistance is experienced by the nanoparticles during the motion that in turn weakens the velocity profile. The same effects were noticed for increase in the unsteadiness parameter with fluid motion.
· Increase in the thin film parameter leads to strengthening of the thickness of the momentum boundary layer,as a result of which the flow characteristics of the fluid improve.
· The transfer of energy increases with increase in the value of the Eckert number, which leads to growth of the thermal profile.
· Increase in the Prandtl number results in a reduction in thermal diffusion that causes a decline in thermal characteristics.
· With increase in the value of the unsteadiness parameter more heat transfer takes place from regions of higher concentration to regions of lower concentration, due to which an enhancement in heat transfer occurs.
· With increasing value of the viscosity parameter, the thickness of the thermal layer is reduced;as a result less heat diffuses and ultimately heat transmission declines.
· It is also established that the rate of thermal flow varies from 3.77%to 9.02%when the values of TiO2nanoparticles range from 0.01 to 0.03 whereas for the same range of values of (TiO2+Ag) nanoparticles the thermal flow rate varies from 4.05% to 9.58% demonstrating that hybrid nanoparticles ensure a greater heat flow rate than a traditional nanofluid.
Acknowledgment
We thank the Deanship of Scientific Research at King Khalid University for funding this work through research groups(Grant No.RGP.1/260/42).
Appendix A
Table A1. Nomenclature.
- Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes

