大型連續Sylvester 方程外推的CSCS 迭代
劉仲云 張芳
(長沙理工大學數學與統計學院,長沙,410114)
1 引言
大型連續Sylvester 方程[1]是最常用的線性矩陣方程之一.矩陣方程形如

這里A ∈Rn×n,B ∈Rm×m,E ∈Rn×m是給定的矩陣.眾所周知,當系數矩陣A和?B沒有公共特征值時,方程(1.1)有唯一解[2,3].
Sylvester 方程是設計Luenberger 觀測的經典方法, 它廣泛應用于信號處理、控制和系統理論[4–7],也常出現在計算不變量子空間的Riccati方程的線性和廣義特征值問題中[8–10],也可用于設計常微分方程數值解的隱式龍格 庫塔積分公式和分塊多步公式中[11].矩形域上分離橢圓邊值問題的有限差分離散產生的方程也可以寫成Sylvester 方程[12,13],優化理論、結構動力學、固體力學、地質分子光學等領域都涉及到Sylvester 方程的求解[14].
求解連續Sylvester 方程(1.1)主要有兩種方法.第一種方法是將矩陣方程(1.1)轉換成一個線性方程Φx=c,這里Φ=Im ?A+BT ?In是矩陣A和BT的Kronecker 積的和,向量x和c是矩陣X和C的列向量,直接法和迭代法均可用于求解該線性方程. 第二種方法是對方程(1.1)進行迭代.
當系數矩陣階數比較大時,線性方程Φx=c中的系數矩陣Φ 的階數會相當大,一般會出現數據存儲和計算時間方面的困難.這說明第一種方法主要用于中小維問題.例如: 文獻[15]中提出的Bartel stewart 方法是基于使用特征值QR 算法將矩陣A和B化為實Schur 形式,然后使用直接法來求解幾個線性方程.文獻[16]提出的Hessenberg Schur 法是將矩陣A化為Hessenberg 形式,將矩陣B分解為擬三角Schur 形式,其速度比Bartels Stewart 方法快.這些方法都屬于直接法,并在MATLAB 中進行了應用.
對于大型稀疏Sylvester 方程,一般用迭代法求解. 比較常見的有古典迭代法,Smith 迭代法[17],ADI 迭代法[18]等. 最近比較流行的迭代法, 是利用系數矩陣A和B的分裂來建立類似ADI 迭代格式的迭代法,例如,白中治在2011 年提出的HSS 迭代法[19].自該方法提出后,幾個更為有效的類似的分裂迭代法相繼出現,例如: 2013 年王湘提出的PSS 迭代法[20], 2014 年鄭青青提出的NSS 迭代法[21]等.這些方法都無條件收斂到方程的精確解.
文獻[1]考慮了(1.1)中系數矩陣A和B都是正定Toeplitz 矩陣的情況,提出了CSCS 迭代法.通過這種CSCS 迭代方法,將求解一般連續Sylvester 方程的問題轉化為包含兩個循環矩陣和反循環矩陣的連續Sylvester 方程的求解問題.通過這種轉化可以利用傅里葉算法快速求解.在對流擴散方程的離散化中就出現了這種結構的矩陣[13,22].
上述這些情況激發了我們對連續Sylvester 方程進一步的研究興趣. 本文提出一個外推的CSCS(ECSCS)迭代.文章的結構如下: 第二節介紹基本定義,第三節介紹CSCS 迭代,第四節給出ECSCS 迭代法,并分析其收斂性,第五節通過數值實驗驗證該方法的有效性.
2 基本定義
對于任意的矩陣K ∈Rn×n,K?,ρ(K)和λ(K)分別表示它的共軛轉置矩陣、譜半徑和特征值.Ki,j是矩陣K的第i行j列元素.若x ∈R,則x的實部記為Re(x),虛部記為Im(x).如果矩陣(K+K?)是正定的,則矩陣K也是正定的.該正定條件也等價于: 存在一個非零向量z ∈R,使得Re(z?Kz)>0,即對于矩陣K的任意特征值λ,有Re(λ)>0[23].
任意一個Toeplitz 矩陣T都有一個循環反循環分裂,即:T=CT+ST,這里CT是循環矩陣,ST是反循環矩陣,定義如下:

眾所周知,循環矩陣C和反循環矩陣S可由傅里葉矩陣F和酉矩陣?F=FD進行如下對角化:

3 CSCS 迭代
若方程(1.1)中的系數矩陣A ∈Rn×n,B ∈Rm×m是正定Toeplitz 矩陣,則矩陣A,B可以進行如下循環反循環分裂:
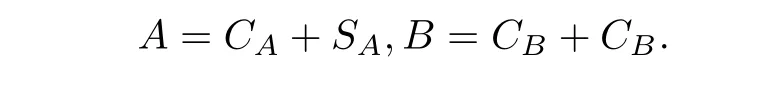
給定常數α,β及適當維數的單位矩陣I,則有
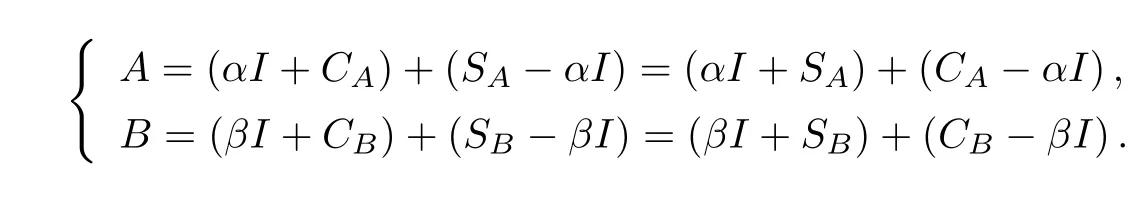
由此可知,連續Sylvester 方程(1.1)可以等價地寫成不動點矩陣方程
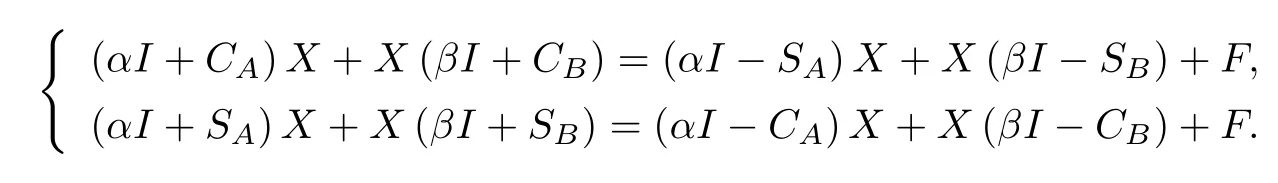
文獻[1]中提出的求解(1.1)的CSCS 迭代定義如下.
CSCS 迭代給定一個初始矩陣X(0)∈Rn×m,使用以下迭代格式計算X(k+1)∈Rn×m(k=0,1,2,···):
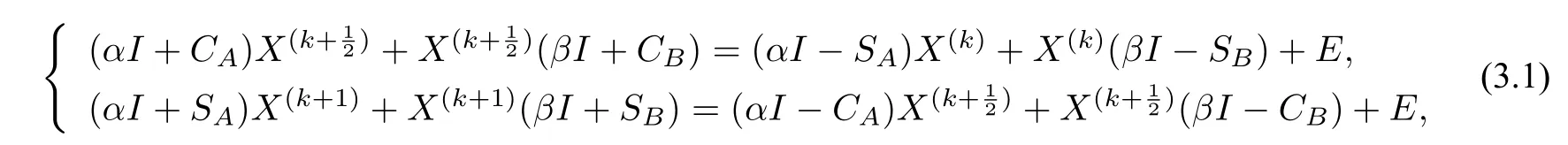
對于上面的CSCS 迭代,文獻[1]證明了如下收斂性定理.

因而,對任意γ>0,有ρ(T(γ))≤σ(γ)<1.
4 ECSCS 迭代
為了進一步加快CSCS 迭代(3.1)的收斂速度,本節給出ECSCS 迭代.
ECSCS 迭代給定一個初始矩陣X(0)∈Rn×m,使用以下迭代格式計算X(k+1)∈Rn×m(k=0,1,2,···):
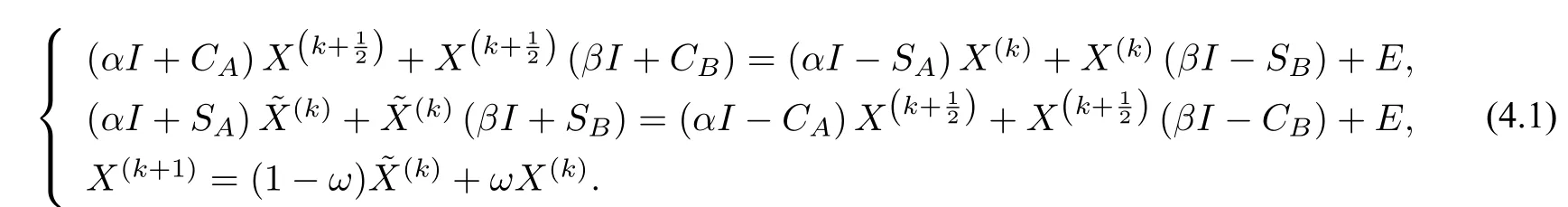
用矩陣向量形式,ECSCS 迭代可以等價為
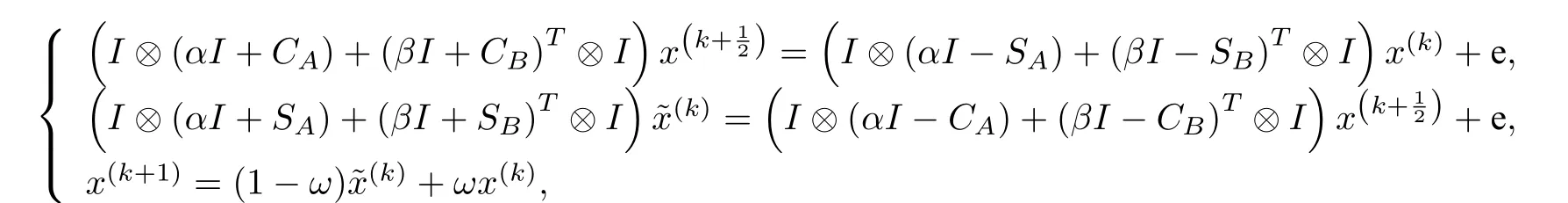
進而變成一步迭代格式

關于ECSCS 迭代,有如下的收斂性定理:
定理2在定理1 的假設下,(4.1)中產生的ECSCS 迭代序列X(k)收斂到(1.1)的精確解X?,其中ω ∈(0,).
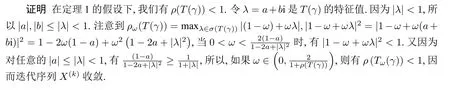
5 數值實驗
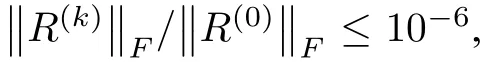
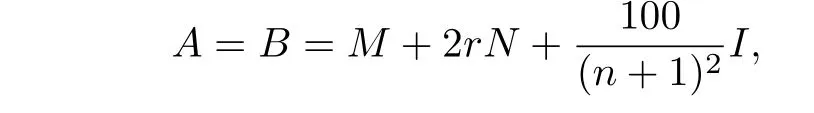
例1 考慮連續Sylvester 方程(1.1),其中矩陣M,N ∈Rn×n都是三對角矩陣:M= tridiag(?1,2,?1),N= tridiag(?0.5,0,0.5). 數值結果見表1和表2.
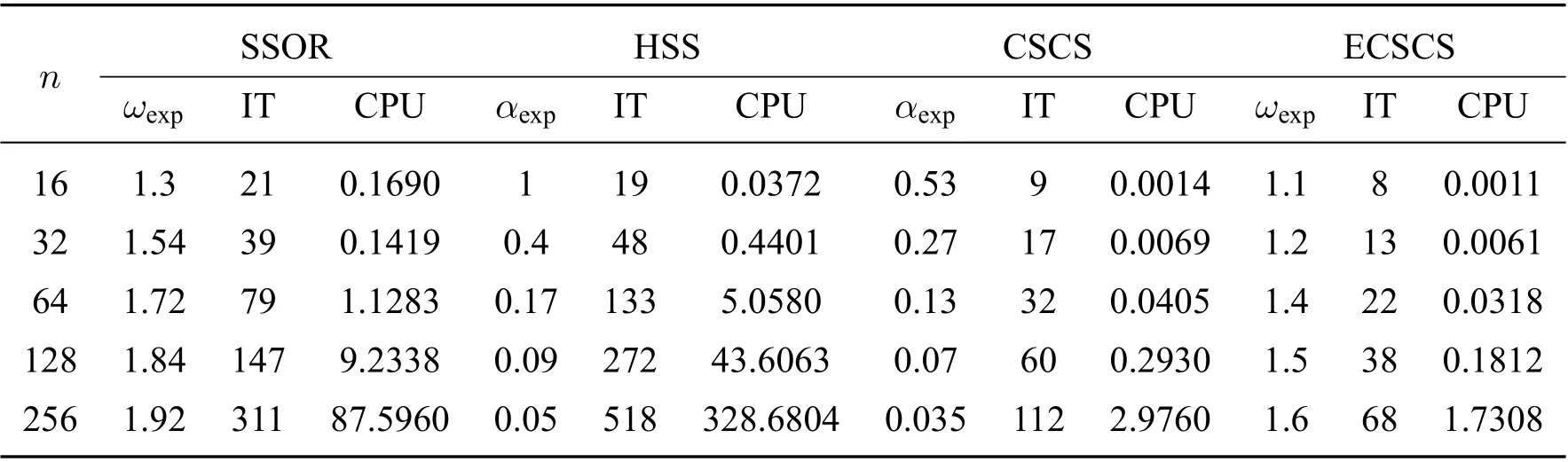
表1 SSOR,HSS,CSCS 和ECSCS 的IT 與CPU
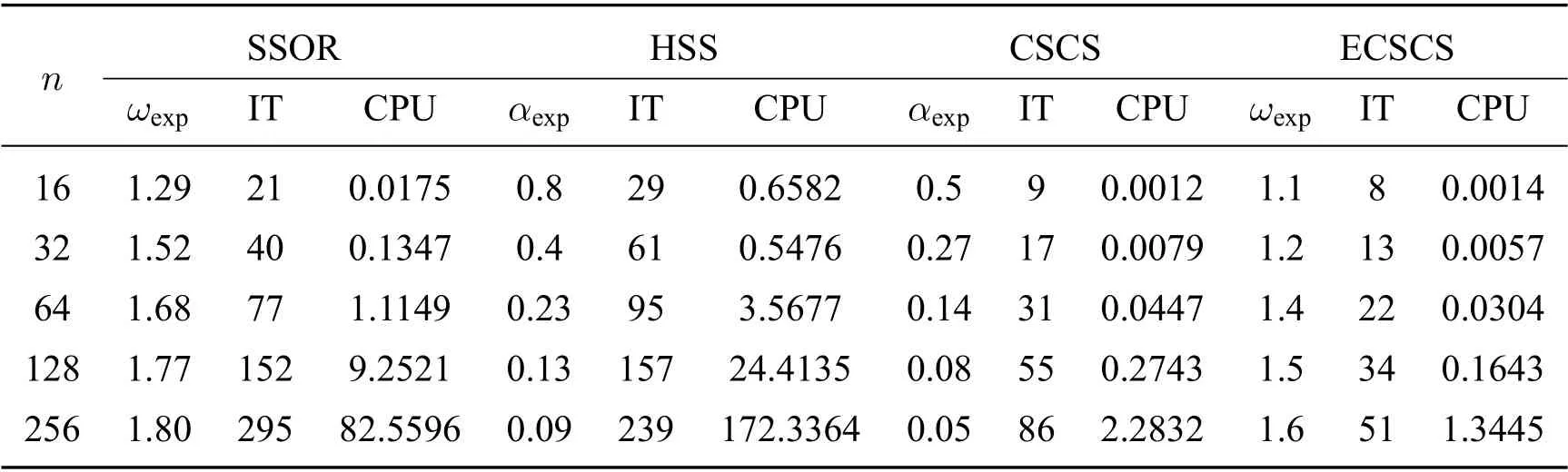
表2 SSOR,HSS,CSCS 和ECSCS 的IT 與CPU
例2 考慮Sylvester 方程(1.1),其中矩陣
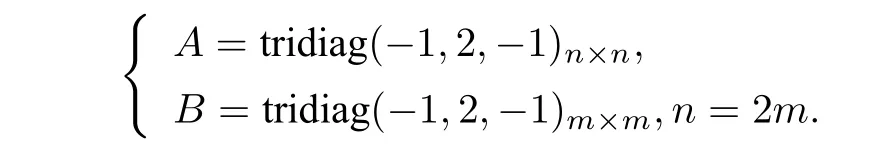
數值結果見表3.

表3 SSOR,HSS,CSCS 和ECSCS 的IT 與CPU
從例1 和例2 中可以看到: CSCS 迭代在迭代次數和計算效率上都優于HSS 迭代和SSOR 迭代,而ECSCS 比CSCS 收斂的效果更好,并且系數矩陣的階數越大,效果越明顯,因此外推的CSCS迭代很好地提高了CSCS 迭代法的收斂速度.

