彈性螺旋槳-軸雙向流固耦合計算
李小軍 沈 杰 劉寒秋
(1. 中國船舶及海洋工程設計研究院 上海 200011; 2. 浙江大學 海洋學院 舟山 316000)
0 引 言
當前船舶螺旋槳大多采用金屬材料,尤其是鎳錳青銅和鎳鋁青銅,其彈性模量較高,在流場中工作時不易變形,水動力性能較為穩定。因此,在以往的螺旋槳設計和性能預報中,大多將螺旋槳視為剛性,不考慮槳葉結構和流體之間的耦合作用。近年來,隨著船舶減振降噪和能效提升的要求越來越高,復合材料螺旋槳和大側斜螺旋槳應用越來越廣泛。復合材料螺旋槳和大側斜螺旋槳在工作時容易發生形變,形變后的槳葉反之也影響流場的分布。因此,常規的“剛性槳”設計與性能預報方法已經不能滿足精度要求,此時必須要考慮螺旋槳的彈性效應。
隨著計算機技術的發展,基于雷諾時均Navier-Stokes方程的計算流體力學(Computational Fluid Dynamics,CFD)和結構有限元(Finite Element Method,FEM)相耦合的方法,已經發展為求解螺旋槳水動力性能和結構特性研究的重要理論方法,且經歷了從單向流固耦合向雙向流固耦合發展的過程。鄒勁等對不同槳轂形狀下的DTMBP4381水動力特性進行雙向流固耦合計算,探討圓柱形槳轂與球形槳轂對該無側斜槳性能影響及作用機理。劉影等通過雙向耦合算法實現復合材料螺旋槳在均勻來流下的流固耦合數值模擬,研究了不同進速系數和不同鋪層角度時復合材料螺旋槳的水動力性能及結構響應。然而,該研究中的螺旋槳仍被視為獨立的研究對象,卻忽略了軸系及其支撐結構的影響。為了考慮槳與軸系間的彈性耦合效應,鄒冬林等利用有限元法(FEM)耦合邊界元法(Boundary Element Method,BEM)建立了流體-彈性槳-軸系雙向流固耦合動力學模型,并通過數值仿真分析以及實驗研究,驗證了所建模型的正確性。
本文建立槳-軸結構三維模型,以鎳鋁青銅合金和玻璃纖維2種材質作為“剛性槳”和“彈性槳”的代表,采用非定常RANS方程和結構有限元相耦合的方法,在ANSYS的Workbench工作臺中進行對槳-軸結構模型進行雙向流固耦合計算,分析螺旋槳的彈性效應對螺旋槳水動力性能以及結構應力應變的影響。
1 力學模型及計算方法
1.1 螺旋槳的運動方程
螺旋槳在流體中工作時的連續性方程和動量方程為:
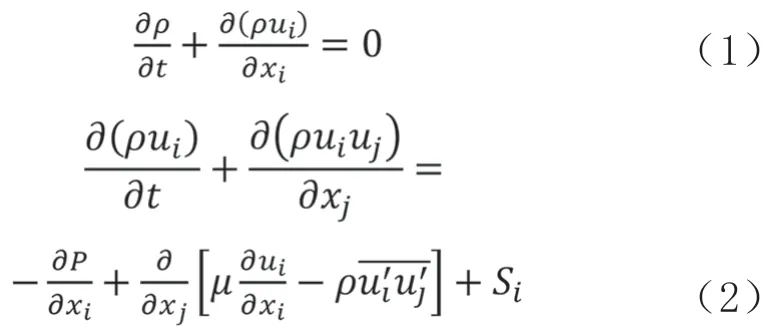
由于流體屬于不可壓縮黏性流體,此時

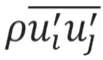
1.2 槳-軸結構的流固耦合方程
考慮到流體作用時,槳-軸結構運動方程如下:
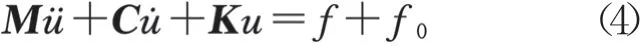
式中:為槳-軸系統的質量矩陣;為槳-軸系統的阻尼矩陣;為槳-軸系統的剛度矩陣;為結構廣義位移矢量;為流體作用在槳葉的壓力矢量,為結構力矢量。
1.3 流固耦合計算方法
由于槳-軸結構的雙向流固耦合不涉及到熱流量和溫度的傳遞,只需要滿足位移和力這2個變量的守恒,即:

式中:為力,N;為位移,m;下標表示結構,下標表示流體。
槳葉和流體之間存在界面耦合。耦合計算時,流體運動和槳葉形變無法進行顯式分離,導致兩個計算域邊界的節點不能一一對應。本文采用任意拉格朗日歐拉方法(Arbitrary Lagrangian-Eulerian,ALE),考慮螺旋槳葉片的大形變,采用隱式迭代進行流體和結構計算。采用局部網格重構法對流體網格進行更新,通過結構域邊界節點位移插值得到流體邊界節點的位移,通過流體域邊界節點的力插值得到結構域的力。邊界的節點對應圖如圖1 所示。
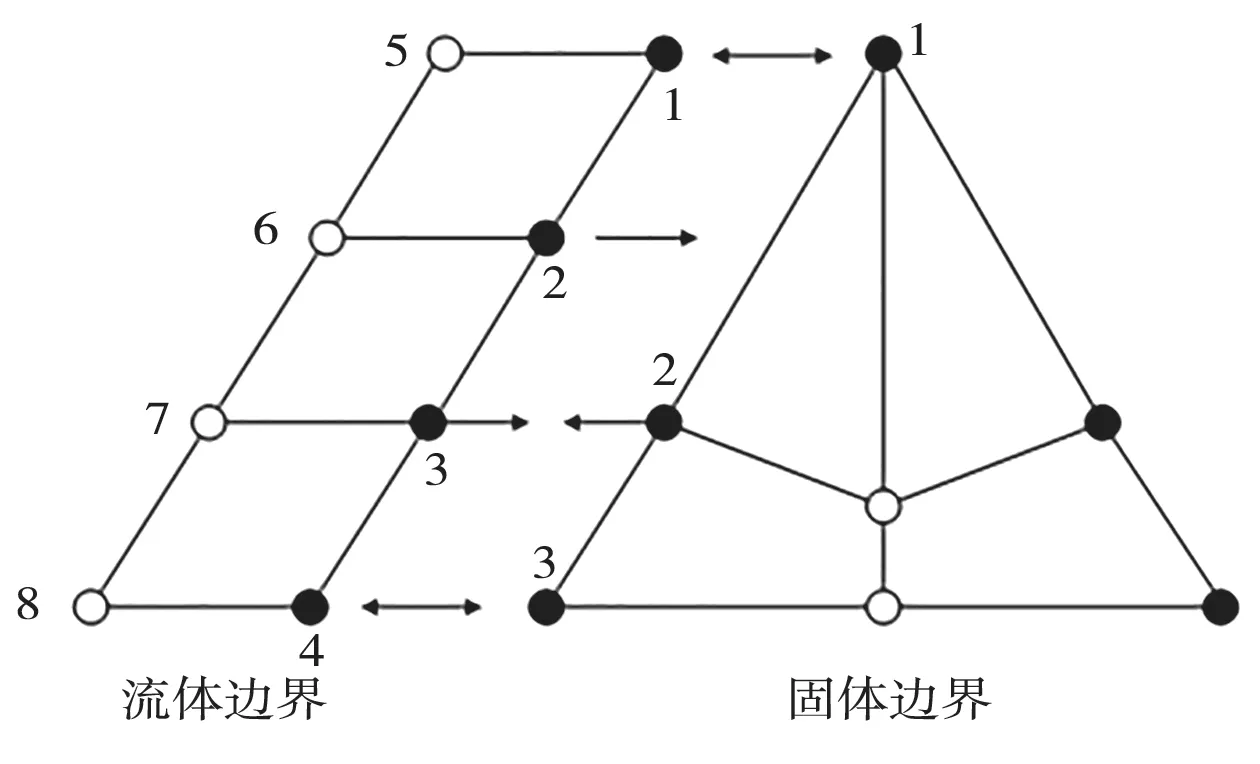
圖1 耦合面上節點對應圖
在ANSYS19.0的Workbench工作臺,采用Fluent模塊和Transient Structural模塊分別求解流場部分和結構部分,兩者之間采用System Coupling模塊相互傳遞位移和載荷的數據。
2 模型建立及參數設置
2.1 模型建立及材料設置
本文選取西江干線某多用途船的螺旋槳和軸系作為研究對象,圖2是該船的推進系統布置圖,螺旋槳和軸系的參數分別如表1和表2所示。
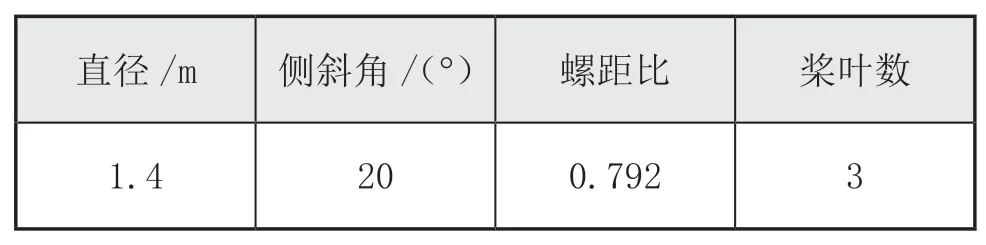
表1 螺旋槳主要參數
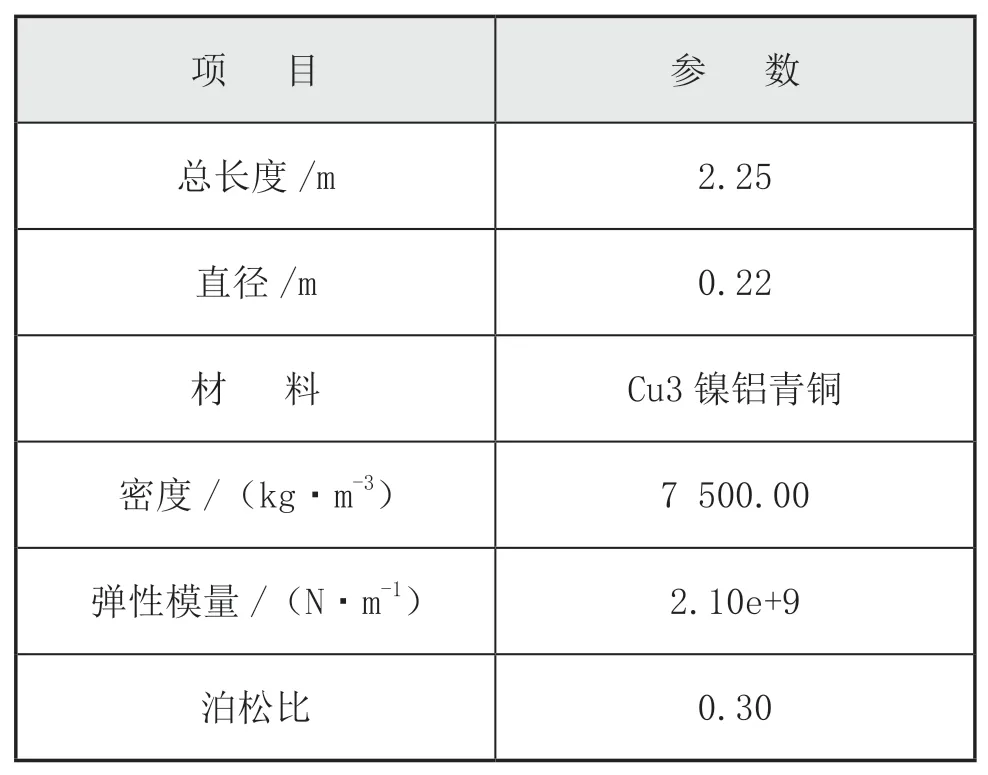
表2 軸系主要尺寸參數
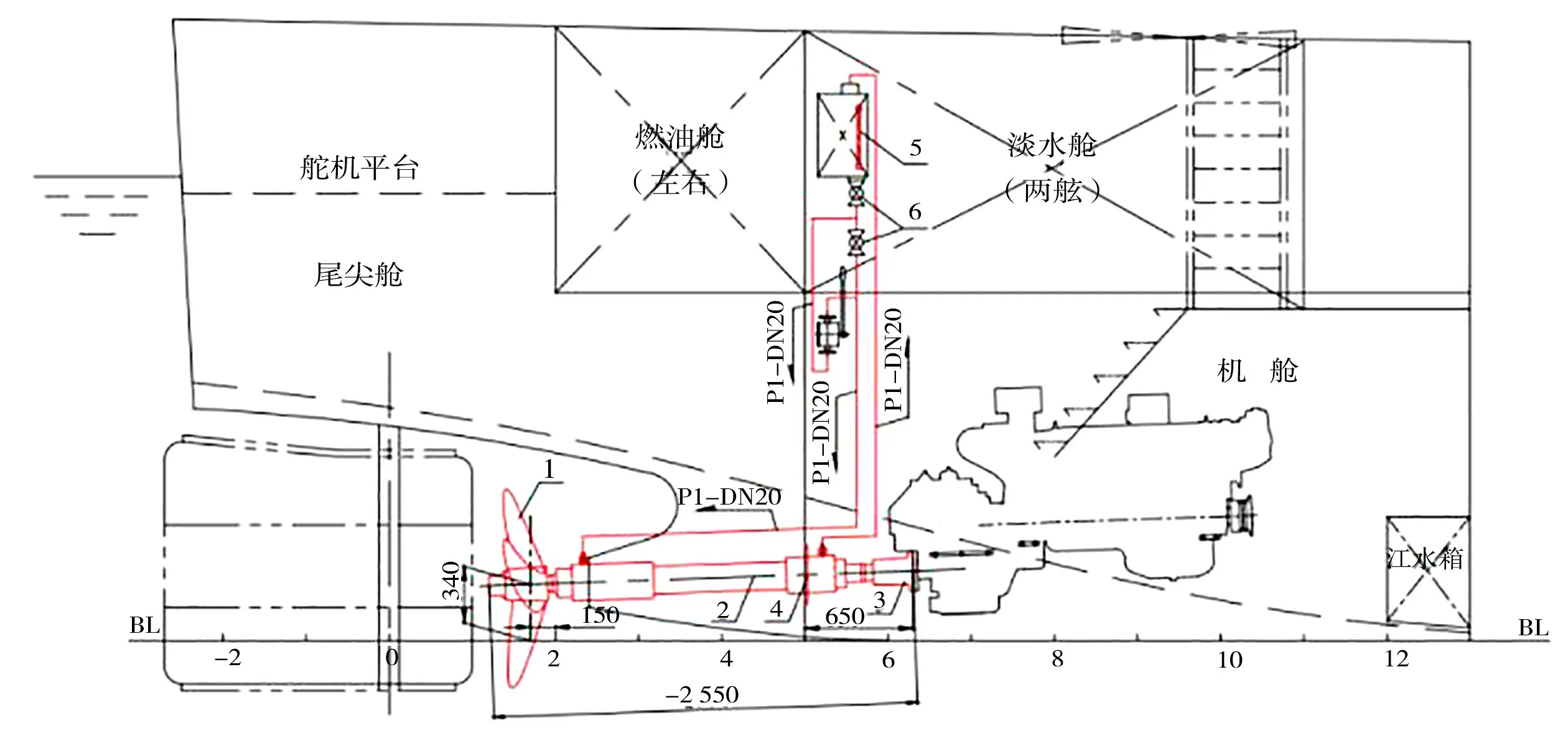
圖2 推進系統布置圖
螺旋槳實物和三維模型如圖3 所示,槳-軸三維模型如圖4 所示。
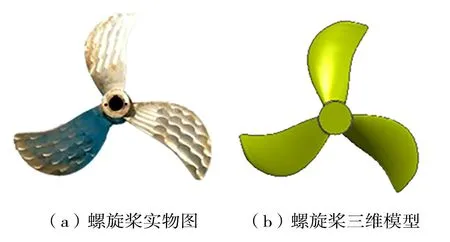
圖3 螺旋槳實物圖及三維模型

圖4 槳-軸三維模型
分別選取鎳鋁青銅合金和玻璃纖維材料作為剛性槳和彈性槳的代表,兩者材料參數如表3所示。
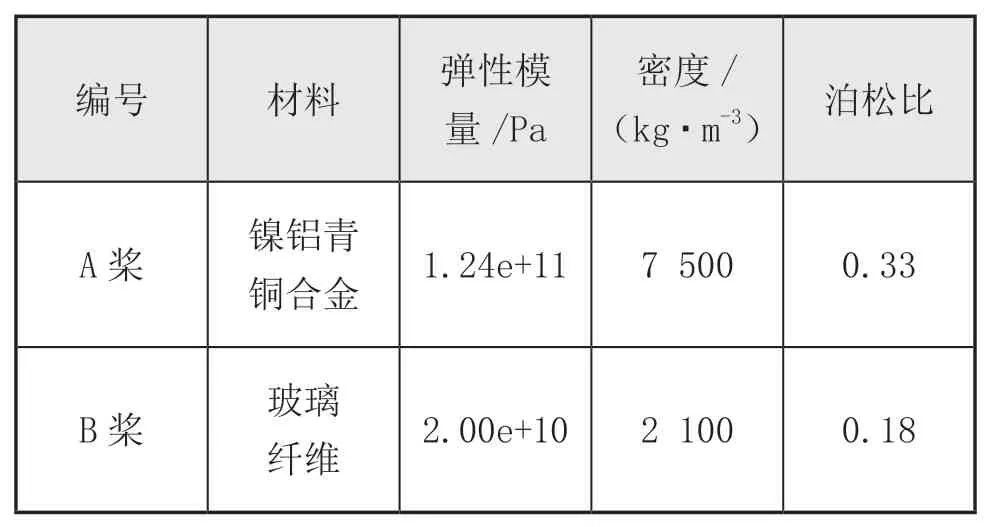
表3 螺旋槳材料參數
2.2 計算的建立及網格劃分
螺旋槳的流場域由旋轉域和靜止域兩部分組成,兩者均為圓柱體。其中旋轉域直徑1.68 m、靜止域直徑6 m、槳葉上游4 m、下游6 m,如圖5所示。
圖5 螺旋槳流體計算域
槳-軸的前后艉軸承采用軸承單元進行Body-Ground連接,水平和垂直剛度均為4.6×10N/m,不考慮其交叉剛度。推力軸承也采用彈簧單元進行Body-Ground連接,約束其近主機端的自由度,如圖6所示。

圖6 槳-軸系統的邊界條件
2.3 耦合求解器設置
進行槳-軸結構雙向流固耦合計算之前,需要先進性單獨流體域的瞬態計算,得到雙向流固耦合的初始值,求解器的具體設置如表4所示。
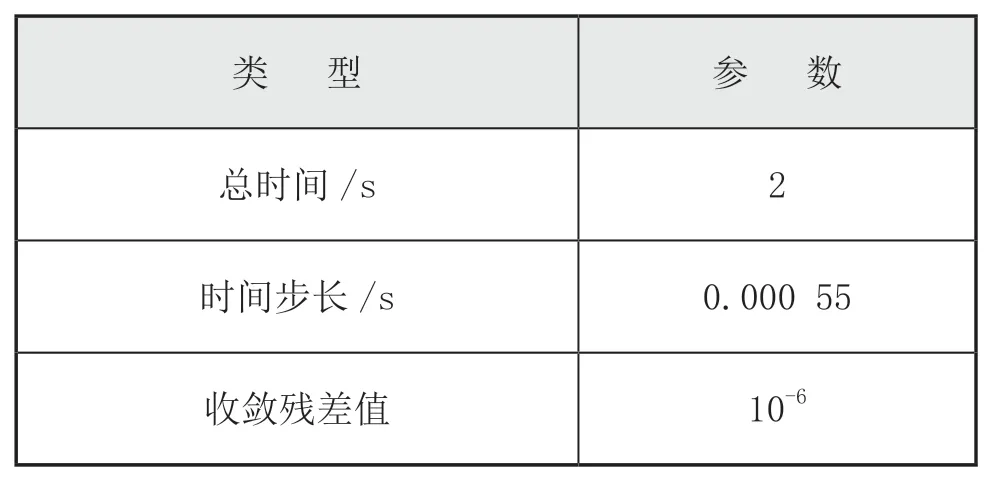
表4 耦合求解器參數表
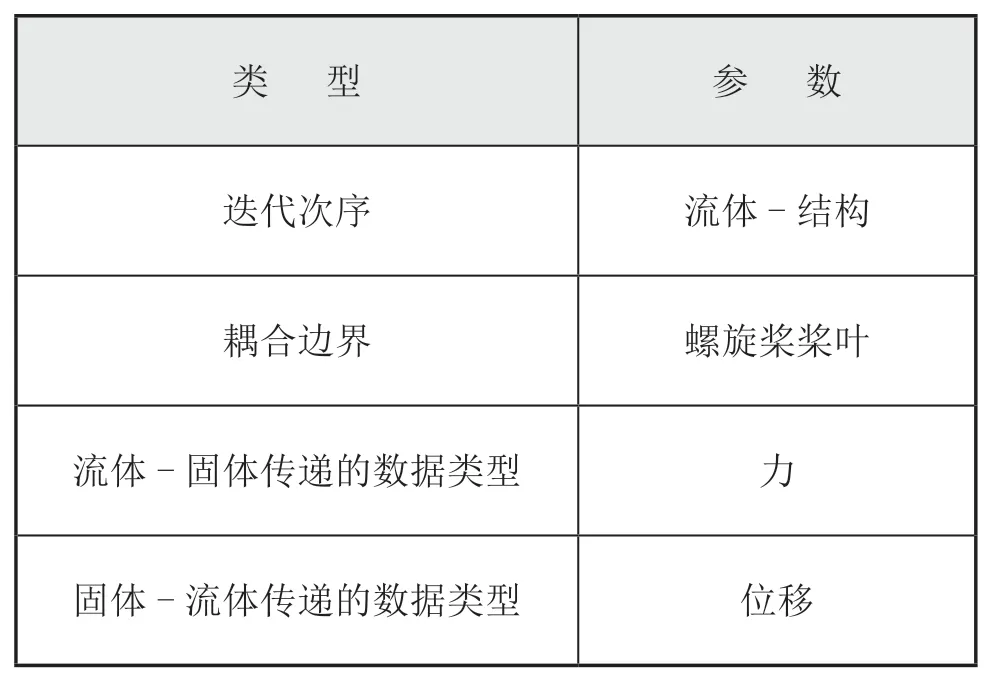
續表4
3 計算結果分析
3.1 數值敞水性能驗證
為驗證螺旋槳模型以及邊界條件設置的準確性,在不考慮槳葉彈性效應的情況下對其進行敞水性能數值計算,其性能指標計算公式如下:
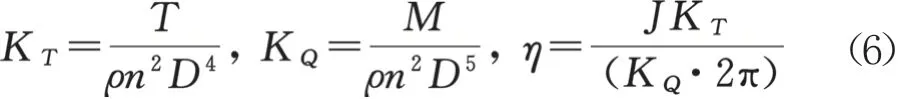
式中:為螺旋槳推力,N;為螺旋槳扭矩,N·m;為水的密度 ,kg/m;為螺旋槳直徑,m。將計算結果與剛性備用槳的水池試驗進行對比,敞水性能結果對比結果如圖7所示,仿真值相對于水池試驗值的誤差如表5所示。
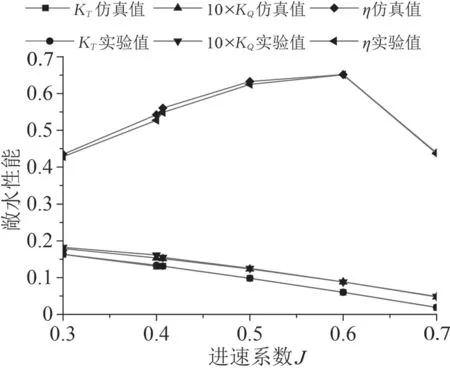
圖7 2種材料螺旋槳的敞水性能曲線
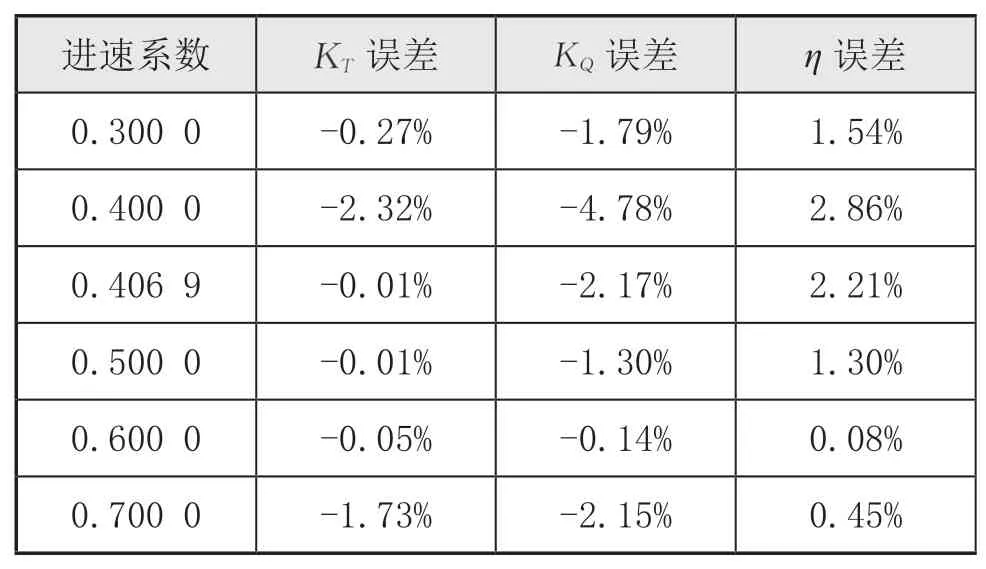
表5 仿真值相對于水池試驗值的誤差表
可以看出,在計算工況下,數值計算與水池試驗的數據基本在5%以內,驗證了該螺旋槳模型的精度和邊界條件的準確性。
3.2 計算穩定性驗證
螺旋槳進速= 0.406 9時,經過2個周期的耦合迭代得到“彈性槳”的槳葉推力、扭矩和槳葉最大變形,以及等效應力隨時間的變化曲線,如圖8所示。
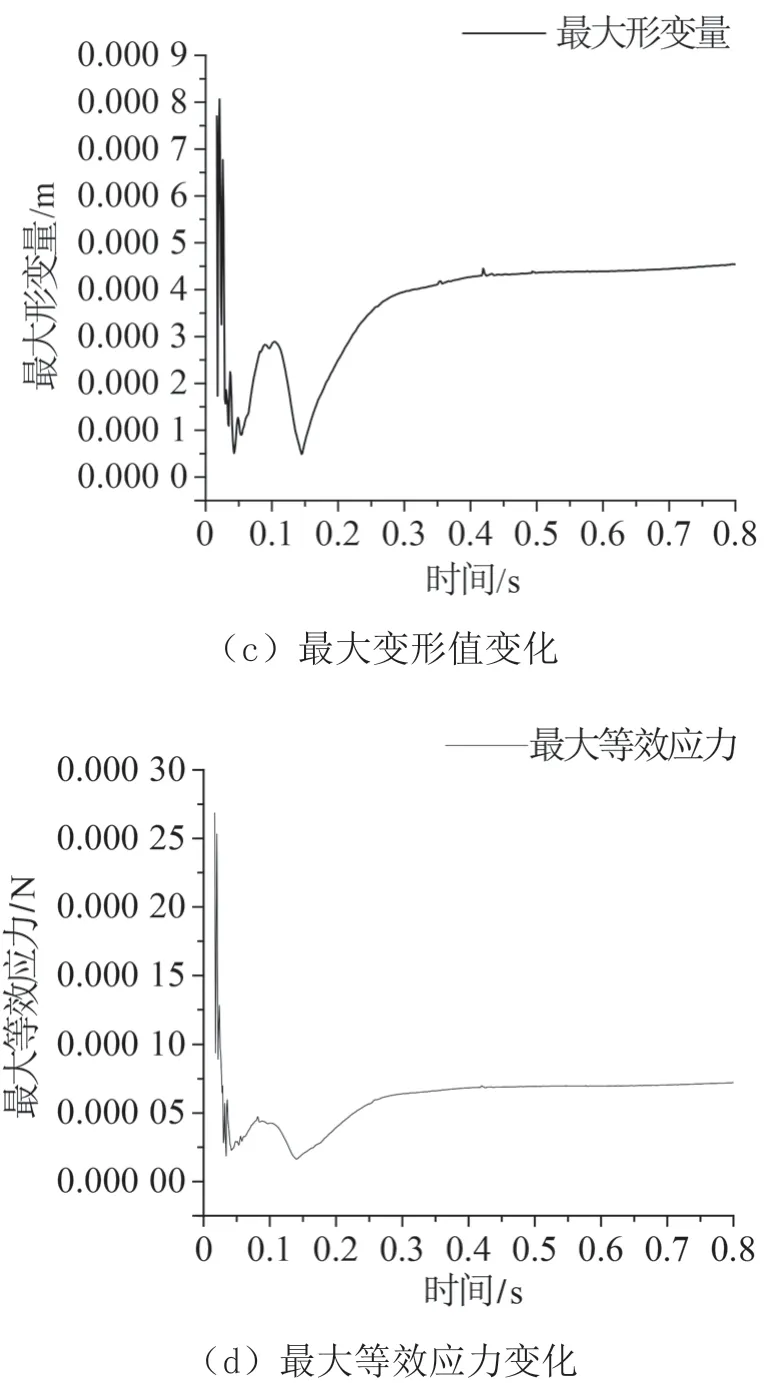
圖8 計算穩定性圖
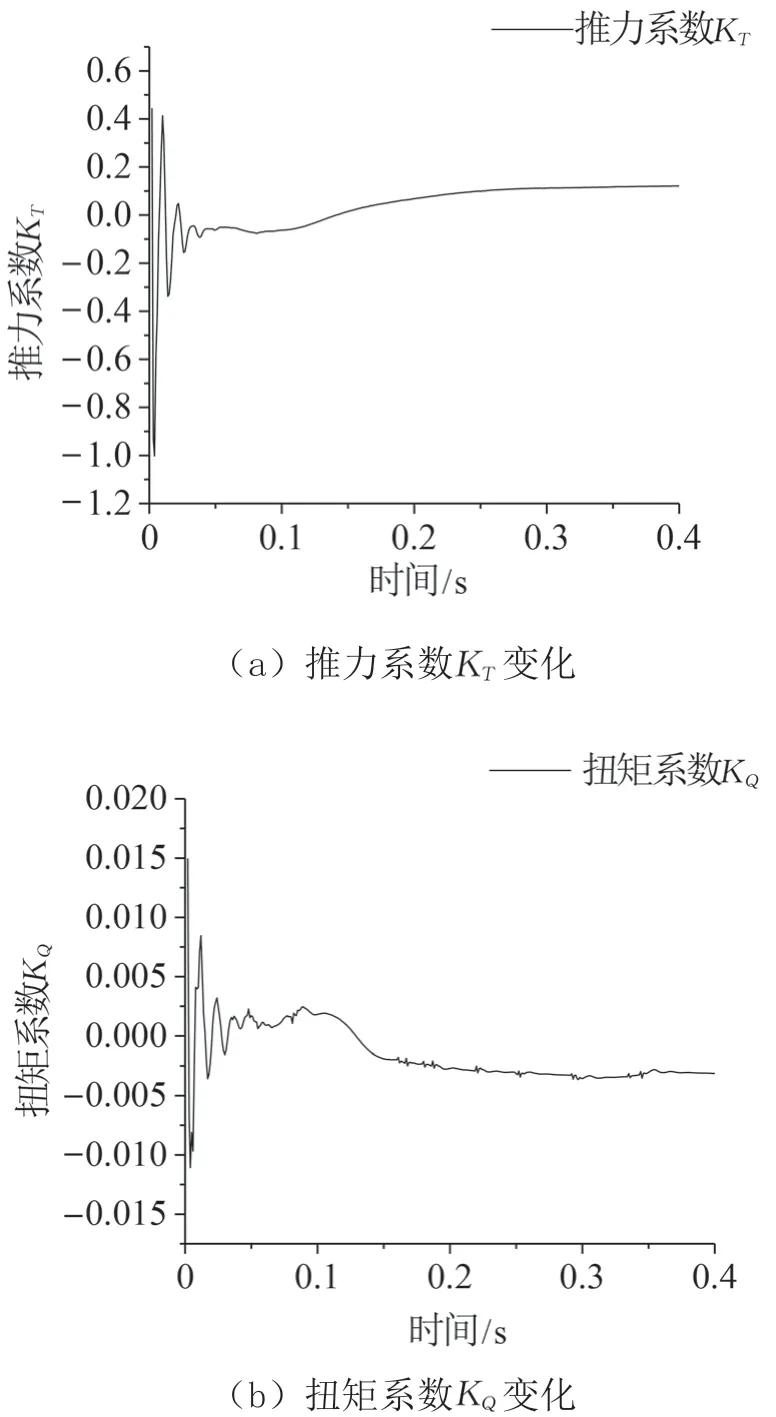
從圖8可以看出:計算從流場域先開始,計算得到的力傳遞到槳葉上產生較大應力和較大位移,經過2個周期的迭代計算合后,其幅值趨于穩定,槳葉最終在平衡位置作周期性振動。
3.3 槳葉彈性效應對水動力性能影響
3.3.1 彈性效應對脈動力影響
在流場中螺旋槳槳葉出口橫截面上設置監測點,監測點半徑為0.6,如圖9所示。
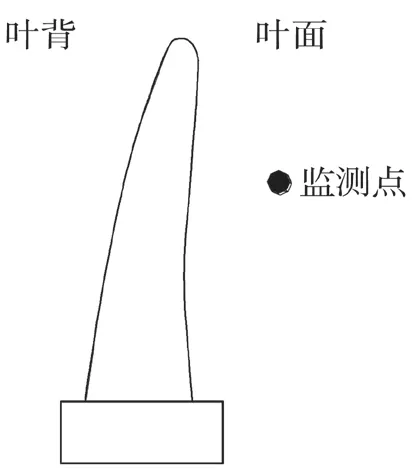
圖9 脈動壓力監測點示意圖
提取螺旋槳旋轉2 周內監測的壓力波動,得到其脈動壓力時域圖,如圖10 所示。為更好地分析壓力脈動的頻率特性,對時域數據進行快速傅里葉變換,略去0 Hz 處的峰值后,得到其脈動壓力的頻域圖,如圖10 所示。
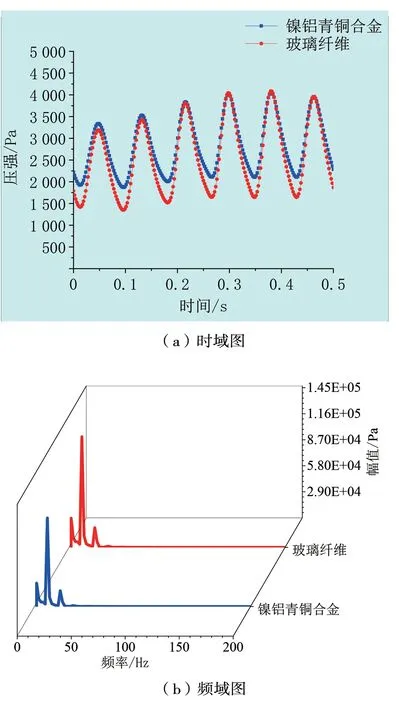
圖10 監測點壓力脈動時域和頻域圖
由圖10可見:在螺旋槳轉動1周范圍內,監測點的脈動壓力值呈周期性,出現3個峰值點,這跟槳葉數對應。且峰值點主要出現在葉頻(12 Hz)和倍葉頻(24 Hz)處,其中葉頻處的峰值最大,這與理論相相符。比較2種不同材料螺旋槳在監測點的壓力脈動,可以看出:隨著槳葉彈性增大,槳葉脈動壓力的幅值的波動范圍增大,這說明槳葉的彈性效應使流場更加不穩定。
3.3.2 彈性效應對槳葉壓力分布影響
取螺旋槳的工作進速=0.406 9,對比2 種材料螺旋槳葉面和葉背的壓力分布,如圖11 所示。可以看出:2 種材料螺旋槳的最大壓力均出現在導邊處,但相對于A 槳,B 槳由于形變量更大,使葉面和葉背的壓力分布更加均勻。
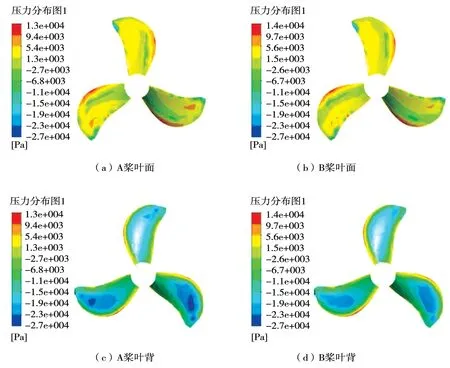
圖11 壓力分布云圖
3.3.3 彈性效應對推進性能影響
取螺旋槳的工作進速=0.406 9,對比耦合前后2 種材料螺旋槳的推力和扭矩(如表6 所示),可以看出:同一進速系數下,相對于A 槳,B 槳由于彈性模量較小,受流固耦合影響較大,推力和扭矩下降都比較明顯。

表6 2 種材料螺旋槳耦合前后對比
取不同進速,對比耦合前后2 種材料螺旋槳的敞水性能值,如下頁圖12 所示。可以看出:2 種材料螺旋槳的推力系數和扭矩系數隨著進速系數的降低而降低。但是在低進速區,由于扭矩比推力的下降幅度大,此時B 槳的敞水效率大于A 槳;高進速區,槳葉所承受的水動力載荷降低,此時B槳的推力下降更明顯,導致其在=0.55~0.7 區域內的敞水效率更低。
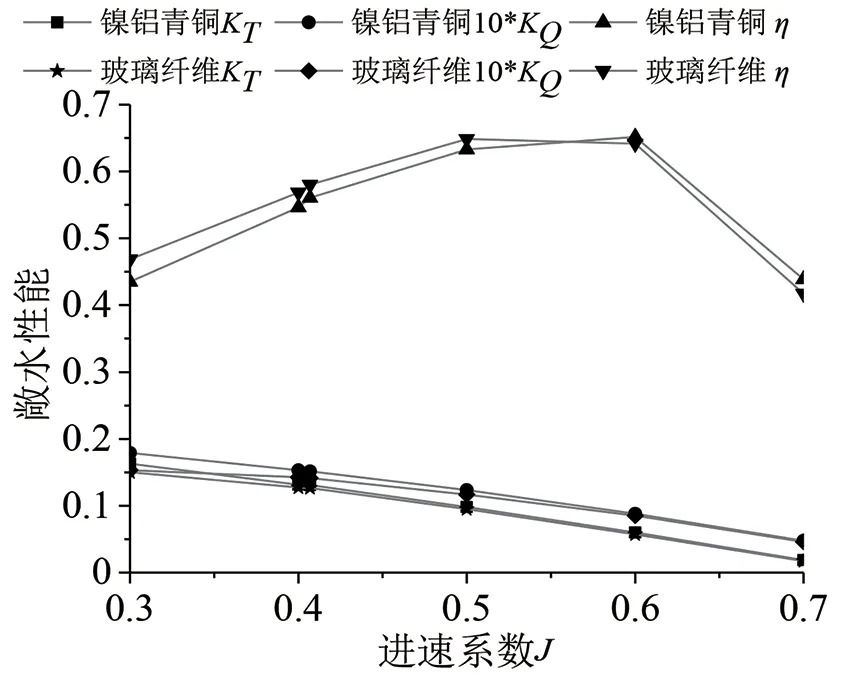
圖12 敞水性能對比
3.4 槳葉彈性效應對螺旋槳結構性能影響
3.4.1 槳葉彈性效應對螺旋槳變形影響
取不同進速,對比2種材料螺旋槳的變形量,如下頁圖13所示。可以看出:隨著進速系數的增加,推力和扭矩值下降導致2種材料螺旋槳的最大 形變均降低,且兩者之間的變形量差距也減小。
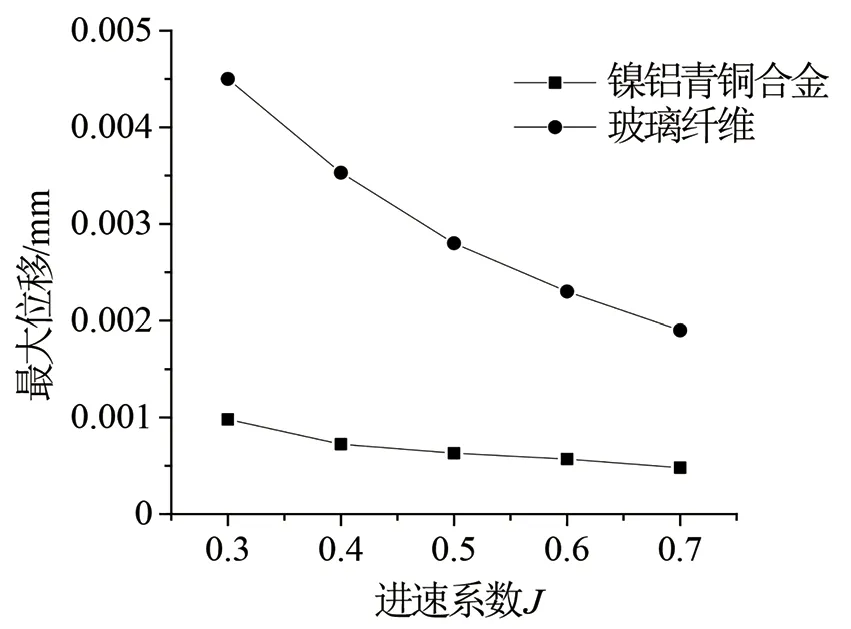
圖13 最大變形量
取工作進速=0.406 9,對比2種材料螺旋槳的變形量,如圖14所示。可以看出:水動力和離心力作用下,發生拉伸和彎曲變形,2種材料螺旋槳的最大變形均在葉梢部位,且A槳的最大變形量遠小于B槳。
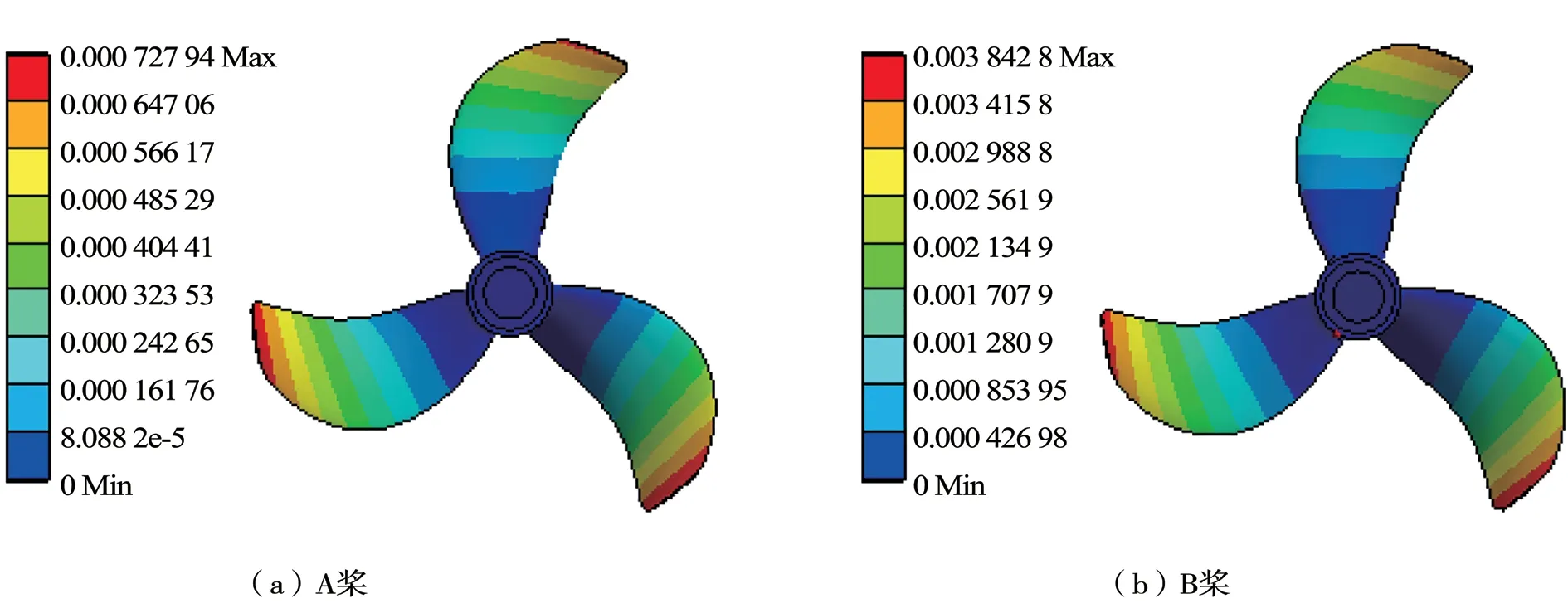
圖14 最大變形對比
3.4.2 槳葉彈性效應對最大等效應力影響
取不同進速,對比2 種材料螺旋槳的等效應力,如圖15 所示。可以看出:隨著進速系數的增大,2 種材料螺旋槳的最大等效應力均降低,其中B 槳的最大等效應力略低于A 槳。
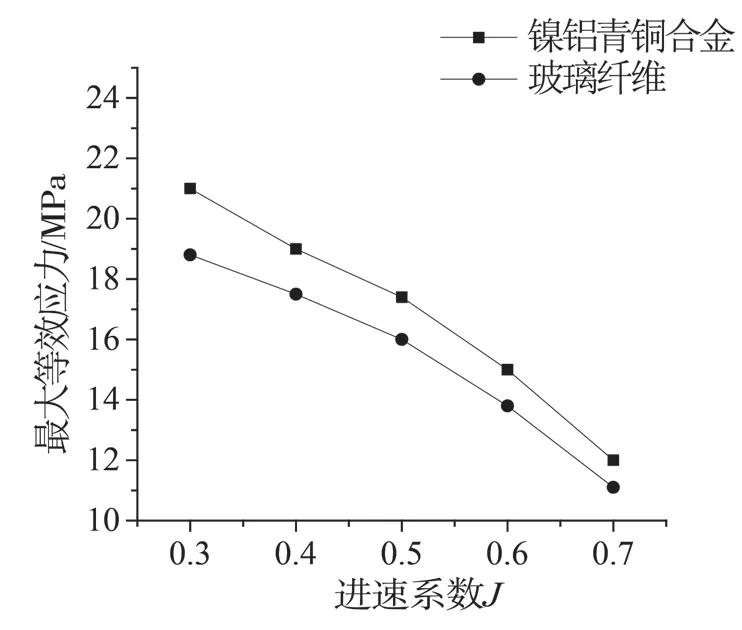
圖15 最大等效應力
取工作進速=0.406 9,對比最大等效應力,可以看出:2 種材料的螺旋槳的最大等效應力均出現在葉根中間部位,且隨著半徑的增大而逐漸減小。其中A 槳的最大等效應力為1.887 8×10Pa,B 槳的最大等效應力為1.612 8×10Pa,參見圖16。這是由于B 槳形彈性變量使流體載荷分布更均,因此其最大等效應力略低于A 槳。
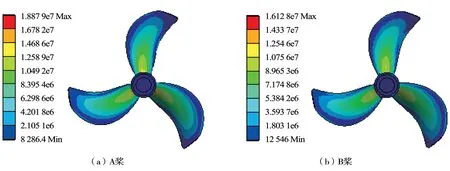
圖16 等效應力對比
4 結 語
本文分別對“彈性槳-軸”結構和“剛性槳-軸”結構進行雙向流固耦合計算,對比分析了水動力性能和結構特性。主要結論如下:槳葉彈性效應所導致的變形對流場的壓力有一定消耗作用,此時作用在槳葉表面的流場壓力分布更加均勻,但流場的脈動壓力波動范圍更大。
本文的研究結論可應用于大型船舶的螺旋槳選型設計、船舶尾部結構減振降噪設計。

